23.1.1 第2课时 正弦和余弦 课件(共22张PPT) 2025-2026学年数学沪科版(2024)九年级上册
文档属性
| 名称 | 23.1.1 第2课时 正弦和余弦 课件(共22张PPT) 2025-2026学年数学沪科版(2024)九年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 475.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 10:58:04 | ||
图片预览



文档简介
(共22张PPT)
沪科版九年级上册 第二十三章
课程讲授
课程导入
习题解析
课堂总结
23.1 锐角的三角函数
第二课时 正弦和余弦
前 言
1.理解并掌握锐角正弦、余弦的定义,并进行相关计算;(重点、难点)
2.在直角三角形中求正弦值、余弦值. (重点)
学习目标及重难点
课程导入
A
B
C
B1
C1
B2
C2
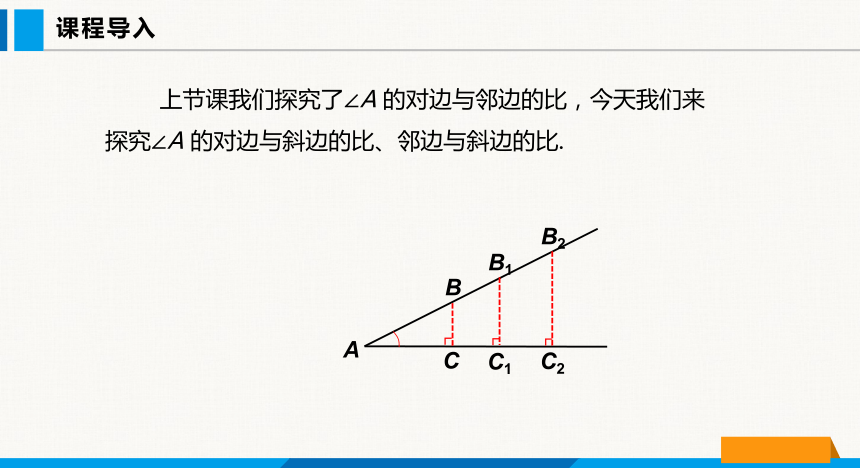
上节课我们探究了∠A 的对边与邻边的比,今天我们来探究∠A 的对边与斜边的比、邻边与斜边的比.
A
B
C
B1
C1
B2
C2
当锐角 A 的大小确定后,∠A 的对边与邻边的比随之确定,那么∠A 的对边与斜边的比、邻边与斜边的比呢?
课程讲授
新课推进
A
B
C
∠A 的邻边 b
∠A 的对边 a
斜边 c
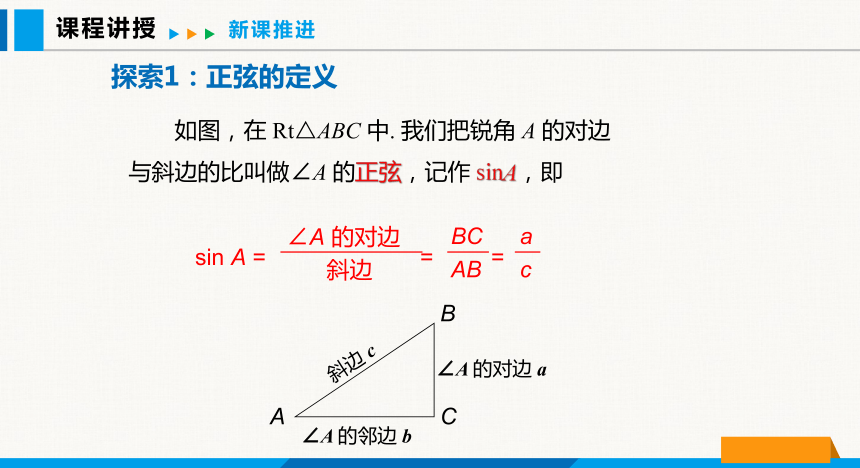
如图,在 Rt△ABC 中. 我们把锐角 A 的对边与斜边的比叫做∠A 的正弦,记作 sinA,即
sin A = = =
∠A 的对边
斜边
BC
AB
a
c
课程讲授
新课推进
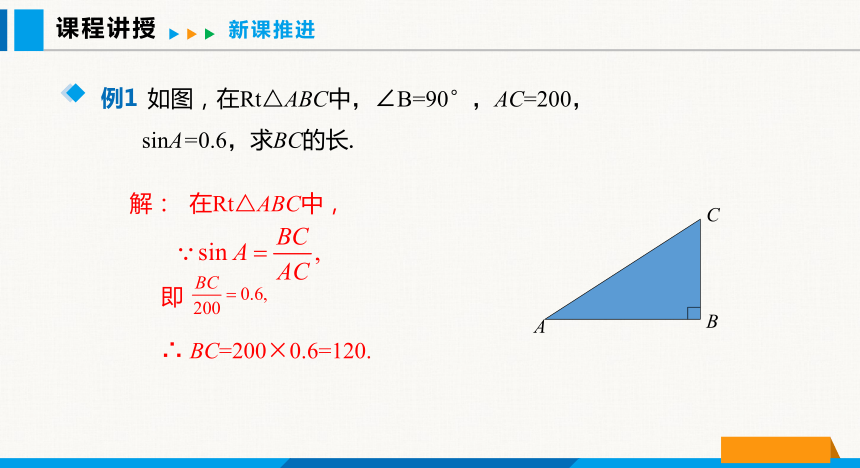
探索1:正弦的定义
如图,在Rt△ABC中,∠B=90°,AC=200,sinA=0.6,求BC的长.
解: 在Rt△ABC中,
即
∴ BC=200×0.6=120.
A
B
C
课程讲授
新课推进
例1
在Rt△ABC中,∠C=90°,BC=20,
求△ABC的周长和面积.
解: 在Rt△ABC中,
20
┐
A
B
C
课程讲授
新课推进
例2
课程讲授
新课推进
A
B
C
∠A 的邻边 b
∠A 的对边 a
斜边 c
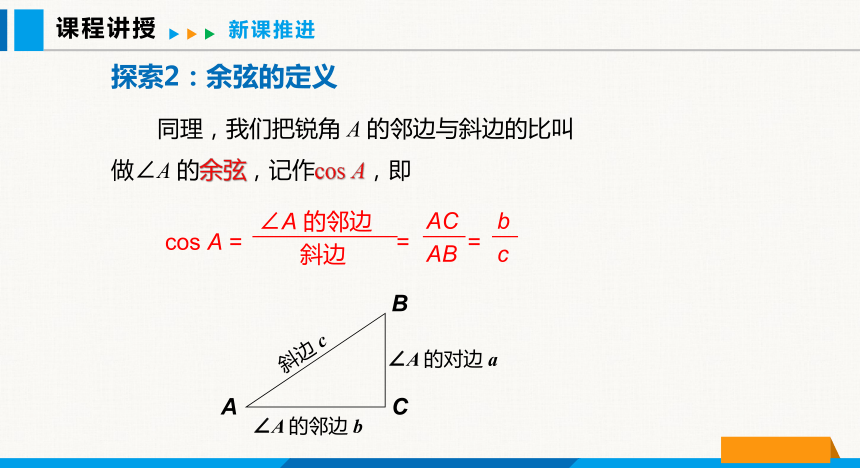
同理,我们把锐角 A 的邻边与斜边的比叫做∠A 的余弦,记作cos A,即
cos A = = =
∠A 的邻边
斜边
AC
AB
b
c
探索2:余弦的定义
课程讲授
新课推进
例3
如图,在 Rt△ABC 中,两直角边 AC = 12,BC = 5,求∠A 的各个三角函数.
A
C
B
12
5
解: 在Rt△ABC 中,AC = 12,
BC = 5,∠C = 90°,得
AB = = 13.
∴ sin A = ,cos A ==
tan A = = .
如图,在平面直角坐标系内有一点P(3,4) ,连接 OP,求 OP 与 x 轴正方向所夹锐角 α 的各个三角函数.
x
y
O
α
P(3,4)
Q
课程讲授
新课推进
例4
解: 过点 P 作 x 轴的垂线,垂足为 Q. 在 Rt△PQO 中,OQ = 3,QP = 4,得
OP = = 5.
∴ sin α =
cos α =
tan α =
课程讲授
新课推进
x
y
O
α
P(3,4)
Q
课程讲授
新课推进
如图,梯子的倾斜程度与sinA和cosA有关系吗?
A
sinA的值越大,梯子越 ____ ;
cosA的值越 ____ ,梯子越陡.
陡
小
8
10
6
8
10
6
A
在 Rt△ABC 中,∠C = 90°,请利用锐角三角函数的定义及勾股定理探索∠A 的正弦、余弦之间的关系.
解:∠A 的正弦、余弦值的平方和等于 1.
例5
课程讲授
新课推进
小结
课程讲授
如图:在Rt △ABC中,∠C=90°,
正弦
余弦
sin A = = =
∠A 的对边
斜边
BC
AB
a
c
COS A = = =
∠A 的邻边
斜边
AC
AB
b
c
A
B
C
∠A 的邻边 b
∠A 的对边 a
斜边 c
小结
课程讲授
定义中应该注意的几个问题:
1.sinA,cosA,tanA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形).
2.sinA,cosA,tanA是一个完整的符号,分别表示∠A的正弦,余弦,正切 (习惯省去“∠”号).
3.sinA,cosA,tanA 是一个比值.注意比的顺序.且sinA,cosA,tanA均>0,无单位.
4.sinA,cosA,tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.
5.角相等,则其三角函数值相等;两锐角的三角函数值相等,则这两个锐角相等.
习题解析
习题1
如图,△ABC 是直角三角形,∠C =90°,AB = 10,AC = 6,求 sin A、cos A、tan A、sin B、cos B、tan B.
A
B
C
10
6
解: 在Rt △ABC 中, ∠C =90°,AB = 10,AC = 6,∴BC = = 8.
sin A =
cos A =
tan A =
sin B =
cos B =
tan B =
习题2
习题解析
如图,在Rt△ABC中,∠C=90°,AC=8,tanA= ,求sinA、cosB的值.
A
B
C
8
解:∵
习题解析
习题3
如图,在正方形ABCD中,M是AD的中点,BE=3AE,求sin∠ECM.
解:设正方形ABCD的边长为4x,∵M是AD的中点,BE=3AE,
∴AM=DM=2x,AE=x,BE=3x.
由勾股定理可知,
A
M
E
D
B
C
A
M
E
D
B
C
由勾股定理逆定理可知,△EMC为直角三角形.
习题解析
如图,在正方形ABCD中,M是AD的中点,BE=3AE,求sin∠ECM.
习题解析
习题4
如图,在平面直角坐标系内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=
(1)求点B的坐标;
(2)求cos∠BAO的值.
A
B
H
解:(1)如图所示,作BH⊥OA, 垂足为H.在Rt△OHB中,
∵BO=5,sin∠BOA= ,
∴BH=3,OH=4,
∴点B的坐标为(4,3).
(2)求cos∠BAO的值.
(2)∵OA=10,OH=4,
∴AH=6.
∵在Rt△AHB中,BH=3,
习题解析
如图,在平面直角坐标系内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=
A
B
H
课程总结
小结
A
B
C
b
a
c
sin A = = =
∠A 的对边
斜边
BC
AB
a
c
cos A = = =
∠A 的邻边
斜边
AC
AB
b
c
tan A = = =
∠A 的对边
∠A 的邻边
BC
AC
a
b
沪科版九年级上册 第二十三章
课程讲授
课程导入
习题解析
课堂总结
23.1 锐角的三角函数
第二课时 正弦和余弦
前 言
1.理解并掌握锐角正弦、余弦的定义,并进行相关计算;(重点、难点)
2.在直角三角形中求正弦值、余弦值. (重点)
学习目标及重难点
课程导入
A
B
C
B1
C1
B2
C2
上节课我们探究了∠A 的对边与邻边的比,今天我们来探究∠A 的对边与斜边的比、邻边与斜边的比.
A
B
C
B1
C1
B2
C2
当锐角 A 的大小确定后,∠A 的对边与邻边的比随之确定,那么∠A 的对边与斜边的比、邻边与斜边的比呢?
课程讲授
新课推进
A
B
C
∠A 的邻边 b
∠A 的对边 a
斜边 c
如图,在 Rt△ABC 中. 我们把锐角 A 的对边与斜边的比叫做∠A 的正弦,记作 sinA,即
sin A = = =
∠A 的对边
斜边
BC
AB
a
c
课程讲授
新课推进
探索1:正弦的定义
如图,在Rt△ABC中,∠B=90°,AC=200,sinA=0.6,求BC的长.
解: 在Rt△ABC中,
即
∴ BC=200×0.6=120.
A
B
C
课程讲授
新课推进
例1
在Rt△ABC中,∠C=90°,BC=20,
求△ABC的周长和面积.
解: 在Rt△ABC中,
20
┐
A
B
C
课程讲授
新课推进
例2
课程讲授
新课推进
A
B
C
∠A 的邻边 b
∠A 的对边 a
斜边 c
同理,我们把锐角 A 的邻边与斜边的比叫做∠A 的余弦,记作cos A,即
cos A = = =
∠A 的邻边
斜边
AC
AB
b
c
探索2:余弦的定义
课程讲授
新课推进
例3
如图,在 Rt△ABC 中,两直角边 AC = 12,BC = 5,求∠A 的各个三角函数.
A
C
B
12
5
解: 在Rt△ABC 中,AC = 12,
BC = 5,∠C = 90°,得
AB = = 13.
∴ sin A = ,cos A ==
tan A = = .
如图,在平面直角坐标系内有一点P(3,4) ,连接 OP,求 OP 与 x 轴正方向所夹锐角 α 的各个三角函数.
x
y
O
α
P(3,4)
Q
课程讲授
新课推进
例4
解: 过点 P 作 x 轴的垂线,垂足为 Q. 在 Rt△PQO 中,OQ = 3,QP = 4,得
OP = = 5.
∴ sin α =
cos α =
tan α =
课程讲授
新课推进
x
y
O
α
P(3,4)
Q
课程讲授
新课推进
如图,梯子的倾斜程度与sinA和cosA有关系吗?
A
sinA的值越大,梯子越 ____ ;
cosA的值越 ____ ,梯子越陡.
陡
小
8
10
6
8
10
6
A
在 Rt△ABC 中,∠C = 90°,请利用锐角三角函数的定义及勾股定理探索∠A 的正弦、余弦之间的关系.
解:∠A 的正弦、余弦值的平方和等于 1.
例5
课程讲授
新课推进
小结
课程讲授
如图:在Rt △ABC中,∠C=90°,
正弦
余弦
sin A = = =
∠A 的对边
斜边
BC
AB
a
c
COS A = = =
∠A 的邻边
斜边
AC
AB
b
c
A
B
C
∠A 的邻边 b
∠A 的对边 a
斜边 c
小结
课程讲授
定义中应该注意的几个问题:
1.sinA,cosA,tanA是在直角三角形中定义的,∠A是锐角(注意数形结合,构造直角三角形).
2.sinA,cosA,tanA是一个完整的符号,分别表示∠A的正弦,余弦,正切 (习惯省去“∠”号).
3.sinA,cosA,tanA 是一个比值.注意比的顺序.且sinA,cosA,tanA均>0,无单位.
4.sinA,cosA,tanA的大小只与∠A的大小有关,而与直角三角形的边长无关.
5.角相等,则其三角函数值相等;两锐角的三角函数值相等,则这两个锐角相等.
习题解析
习题1
如图,△ABC 是直角三角形,∠C =90°,AB = 10,AC = 6,求 sin A、cos A、tan A、sin B、cos B、tan B.
A
B
C
10
6
解: 在Rt △ABC 中, ∠C =90°,AB = 10,AC = 6,∴BC = = 8.
sin A =
cos A =
tan A =
sin B =
cos B =
tan B =
习题2
习题解析
如图,在Rt△ABC中,∠C=90°,AC=8,tanA= ,求sinA、cosB的值.
A
B
C
8
解:∵
习题解析
习题3
如图,在正方形ABCD中,M是AD的中点,BE=3AE,求sin∠ECM.
解:设正方形ABCD的边长为4x,∵M是AD的中点,BE=3AE,
∴AM=DM=2x,AE=x,BE=3x.
由勾股定理可知,
A
M
E
D
B
C
A
M
E
D
B
C
由勾股定理逆定理可知,△EMC为直角三角形.
习题解析
如图,在正方形ABCD中,M是AD的中点,BE=3AE,求sin∠ECM.
习题解析
习题4
如图,在平面直角坐标系内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=
(1)求点B的坐标;
(2)求cos∠BAO的值.
A
B
H
解:(1)如图所示,作BH⊥OA, 垂足为H.在Rt△OHB中,
∵BO=5,sin∠BOA= ,
∴BH=3,OH=4,
∴点B的坐标为(4,3).
(2)求cos∠BAO的值.
(2)∵OA=10,OH=4,
∴AH=6.
∵在Rt△AHB中,BH=3,
习题解析
如图,在平面直角坐标系内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=
A
B
H
课程总结
小结
A
B
C
b
a
c
sin A = = =
∠A 的对边
斜边
BC
AB
a
c
cos A = = =
∠A 的邻边
斜边
AC
AB
b
c
tan A = = =
∠A 的对边
∠A 的邻边
BC
AC
a
b
