14.2 三角形全等的判定 教案 沪科版(2024)数学八年级上册
文档属性
| 名称 | 14.2 三角形全等的判定 教案 沪科版(2024)数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 73.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 11:14:28 | ||
图片预览


文档简介
14.2 三角形全等的判定
一、内容和内容解析
1. 内容:
本节是三角形全等判定的第六课时,主要内容是构建三角形全等条件的探索思路,以及如何利用学习的判定方法证明两个三角形全等。
2. 内容解析:
本节课的内容是在学习了全等三角形的概念、全等三角形的性质、全等三角形的判定后展开的,来探究简捷地判定两个三角形全等的方法。为此构建了三角形全等条件的探索思路,即从“不同条件”开始,分别进行探究.全等三角形是两个三角形最简单、最常见的关系,它不仅是学习知识的基础,而且也是证明线段相等、角相等的重要依据,学生只有很好的掌握了全等三角形的判定方法,并且能灵活地运用它,才能为以后学习三角形相似、《四边形》、《圆》等知识打下良好的基础。
基于以上分析,确定本节课的教学重点:构建三角形全等条件的探索思路,灵活利用判定方法证明两个三角形全等。
二、目标和目标解析:
1、经历探索三角形全等证明的过程,体验根据不同条件灵活运用判定方法解决问题的过程,培养学生的动手能力以及发现、归纳、总结问题的能力。
2、掌握三角形全等判定的方法,应用条件判定两个三角形全等,能够进行有条理的思考并进行简单的推理。
3、在探究三角形全等的条件的过程中,以观察思考、动手画图、合作交流等多种形式让学生共同探讨,培养学生的协作精神。引导学生从现实的生活经历与体验出发,激发学生学习兴趣。
三、教学问题诊断分析:
学生已学过线段、角、相交线、平行线以及三角形的有关知识,并且七年级已接触过推理证明内容,这些都为本课学习全等三角形的判定做好了准备。在证明两个三角形全等时,有部分学生分析不出题中缺少的条件,没有提前去证明这些没有直接给出的条件,就直接证明全等了。
基于以上分析,确定本节课的教学难点:探究三角形全等判定的过程。“分类讨论”的数学方法的渗透和逻辑思维能力的培养也是本节的难点。为了解决教学重难点,渗透数学思想和培养学生思维能力,本节课安排了一个例题、两道练习题和两道习题讲解。
四、学生活动需准备的材料:直尺、三角板。
五、教学支持:
多媒体
六、教学过程设计:
1、问题引入
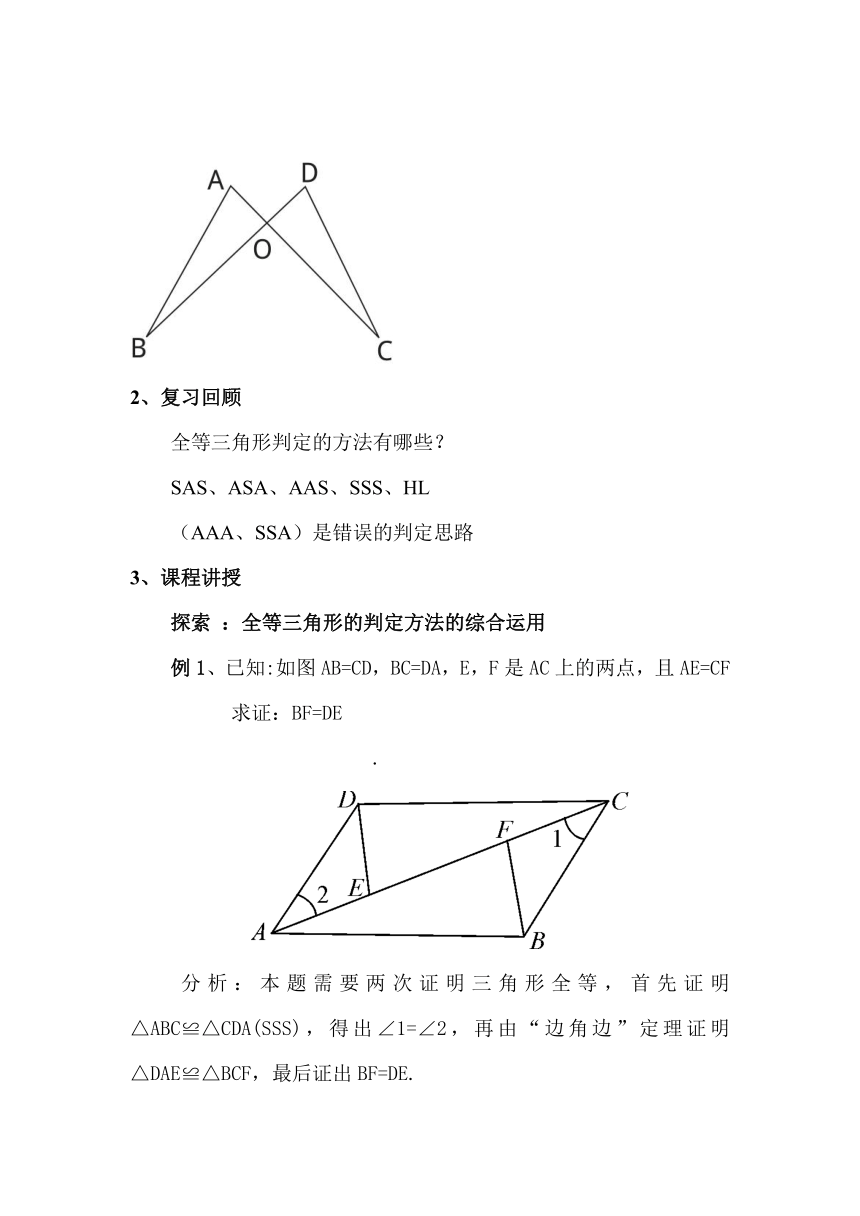
小龙同学编了这样一道题:如图,已知AB=CD,∠A=∠D,AO=DO.求证:△ABO≌△DCO.老师说他的已知条件给多了,请你帮他去掉一个已知条件: AO=DO(或AB=CD)
2、复习回顾
全等三角形判定的方法有哪些?
SAS、ASA、AAS、SSS、HL
(AAA、SSA)是错误的判定思路
3、课程讲授
探索 :全等三角形的判定方法的综合运用
例1、已知:如图AB=CD,BC=DA,E,F是AC上的两点,且AE=CF求证:BF=DE
.
分析:本题需要两次证明三角形全等,首先证明△ABC≌△CDA(SSS),得出∠1=∠2,再由“边角边”定理证明△DAE≌△BCF,最后证出BF=DE.
4.课堂练习:
、如图,已知CA=CB,AD=BD,M,N分别是CA,CB的中点,
求证:DM=DN.
(
A
F
C
E
D
B
)(2)、如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF.求证:BF=DE.
5.习题解析
习题1:如图,CD⊥AB于D点,BE⊥AC于E点,BE、CD交于O点,且AO平分∠BAC.求证:OB=OC.
习题2 :如图,已知,OB=OC,∠B=∠C,求证:OA平分∠BAC.
(
A
O
B
C
) (
)
让学生先独立思考,然后在教师的引导下,分析题意、找出已知条件和缺少的条件,从而找到由已知推出求证的途径。学生口述推理过程,教师板演推理过程。
此环节,教师要给学生写出证明三角形全等的步骤,顺着推理的思路一步步写出来,同时要强调书写格式的规范。
6、课堂小结:
回顾本节课对知识的研究探索过程,小结方法及结论,提炼数学思想,掌握数学规律。
分类讨论是本节课重要的一种数学思想,从头到尾都贯穿于学生的学习中。这节课同学们除了要掌握判定三角形全等的方法,关键是学会如何探究三角形全等的判定.
7、板书设计:
14.2 三角形全等的判定
三角形全等的判定:SAS、ASA、AAS、SSS、HL
复习导入
例题讲解
巩固练习
习题解析
课堂小结
课后作业
一、内容和内容解析
1. 内容:
本节是三角形全等判定的第六课时,主要内容是构建三角形全等条件的探索思路,以及如何利用学习的判定方法证明两个三角形全等。
2. 内容解析:
本节课的内容是在学习了全等三角形的概念、全等三角形的性质、全等三角形的判定后展开的,来探究简捷地判定两个三角形全等的方法。为此构建了三角形全等条件的探索思路,即从“不同条件”开始,分别进行探究.全等三角形是两个三角形最简单、最常见的关系,它不仅是学习知识的基础,而且也是证明线段相等、角相等的重要依据,学生只有很好的掌握了全等三角形的判定方法,并且能灵活地运用它,才能为以后学习三角形相似、《四边形》、《圆》等知识打下良好的基础。
基于以上分析,确定本节课的教学重点:构建三角形全等条件的探索思路,灵活利用判定方法证明两个三角形全等。
二、目标和目标解析:
1、经历探索三角形全等证明的过程,体验根据不同条件灵活运用判定方法解决问题的过程,培养学生的动手能力以及发现、归纳、总结问题的能力。
2、掌握三角形全等判定的方法,应用条件判定两个三角形全等,能够进行有条理的思考并进行简单的推理。
3、在探究三角形全等的条件的过程中,以观察思考、动手画图、合作交流等多种形式让学生共同探讨,培养学生的协作精神。引导学生从现实的生活经历与体验出发,激发学生学习兴趣。
三、教学问题诊断分析:
学生已学过线段、角、相交线、平行线以及三角形的有关知识,并且七年级已接触过推理证明内容,这些都为本课学习全等三角形的判定做好了准备。在证明两个三角形全等时,有部分学生分析不出题中缺少的条件,没有提前去证明这些没有直接给出的条件,就直接证明全等了。
基于以上分析,确定本节课的教学难点:探究三角形全等判定的过程。“分类讨论”的数学方法的渗透和逻辑思维能力的培养也是本节的难点。为了解决教学重难点,渗透数学思想和培养学生思维能力,本节课安排了一个例题、两道练习题和两道习题讲解。
四、学生活动需准备的材料:直尺、三角板。
五、教学支持:
多媒体
六、教学过程设计:
1、问题引入
小龙同学编了这样一道题:如图,已知AB=CD,∠A=∠D,AO=DO.求证:△ABO≌△DCO.老师说他的已知条件给多了,请你帮他去掉一个已知条件: AO=DO(或AB=CD)
2、复习回顾
全等三角形判定的方法有哪些?
SAS、ASA、AAS、SSS、HL
(AAA、SSA)是错误的判定思路
3、课程讲授
探索 :全等三角形的判定方法的综合运用
例1、已知:如图AB=CD,BC=DA,E,F是AC上的两点,且AE=CF求证:BF=DE
.
分析:本题需要两次证明三角形全等,首先证明△ABC≌△CDA(SSS),得出∠1=∠2,再由“边角边”定理证明△DAE≌△BCF,最后证出BF=DE.
4.课堂练习:
、如图,已知CA=CB,AD=BD,M,N分别是CA,CB的中点,
求证:DM=DN.
(
A
F
C
E
D
B
)(2)、如图,AB=CD, BF⊥AC,DE⊥AC,AE=CF.求证:BF=DE.
5.习题解析
习题1:如图,CD⊥AB于D点,BE⊥AC于E点,BE、CD交于O点,且AO平分∠BAC.求证:OB=OC.
习题2 :如图,已知,OB=OC,∠B=∠C,求证:OA平分∠BAC.
(
A
O
B
C
) (
)
让学生先独立思考,然后在教师的引导下,分析题意、找出已知条件和缺少的条件,从而找到由已知推出求证的途径。学生口述推理过程,教师板演推理过程。
此环节,教师要给学生写出证明三角形全等的步骤,顺着推理的思路一步步写出来,同时要强调书写格式的规范。
6、课堂小结:
回顾本节课对知识的研究探索过程,小结方法及结论,提炼数学思想,掌握数学规律。
分类讨论是本节课重要的一种数学思想,从头到尾都贯穿于学生的学习中。这节课同学们除了要掌握判定三角形全等的方法,关键是学会如何探究三角形全等的判定.
7、板书设计:
14.2 三角形全等的判定
三角形全等的判定:SAS、ASA、AAS、SSS、HL
复习导入
例题讲解
巩固练习
习题解析
课堂小结
课后作业
