河南省南阳市淅川县部分学校2025届九年级下学期中考二模数学试卷(含答案)
文档属性
| 名称 | 河南省南阳市淅川县部分学校2025届九年级下学期中考二模数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 281.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 14:54:12 | ||
图片预览




文档简介
2025年河南省南阳市淅川县部分学校中考数学二模试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.负数的概念最早出现在《九章算术》中,把向东走2km记做“+2km”,向西走1km应记做( )
A. -2km B. -1km C. 1km D. +2km
2.DeepSeek,全称杭州深度求索人工智能基础技术研究有限公司,截至2025年2月9日,Deep-Seek的累计下载量已超过1.1亿次,周活跃用户规模高达9700万.其中9700万用科学记数法表示为( )
A. 9700×104 B. 97×106 C. 9.7×107 D. 0.97×108
3.下列计算正确的是( )
A. (a3)n+1=a3n+1 B. (-a2)3 a6=a12
C. a8m a8m=2a16m D. (-m)(-m)4=-m5
4.如图是一个由5个相同的正方体组成的立体图形,它的主视图是( )
A.
B.
C.
D.
5.已知二元一次方程组,则x-y的值为( )
A. 2 B. -2 C. 4 D. -4
6.如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB′关于直线AD对称,点B的对称点是点B′,则∠CAB′的度数为( )
A. 10° B. 20° C. 30° D. 40°
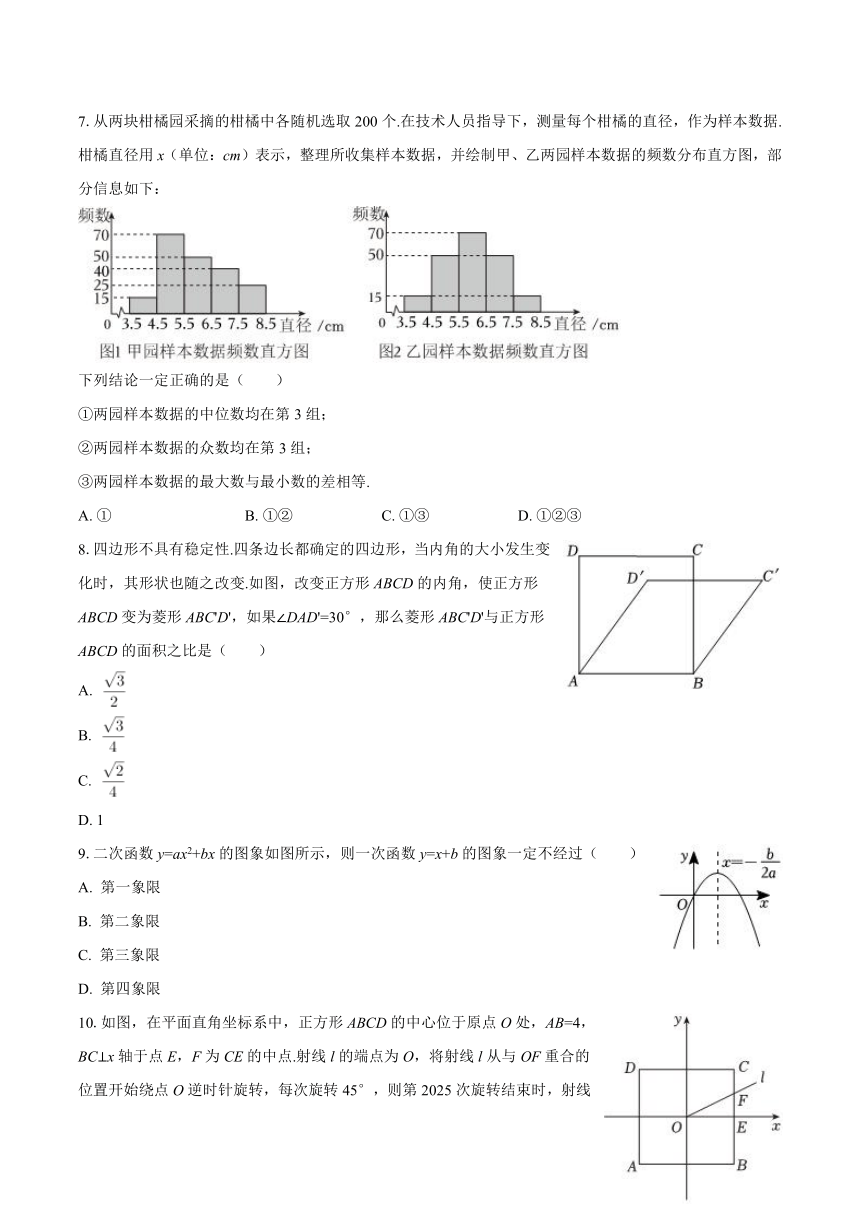
7.从两块柑橘园采摘的柑橘中各随机选取200个.在技术人员指导下,测量每个柑橘的直径,作为样本数据.柑橘直径用x(单位:cm)表示,整理所收集样本数据,并绘制甲、乙两园样本数据的频数分布直方图,部分信息如下:
下列结论一定正确的是( )
①两园样本数据的中位数均在第3组;
②两园样本数据的众数均在第3组;
③两园样本数据的最大数与最小数的差相等.
A. ① B. ①② C. ①③ D. ①②③
8.四边形不具有稳定性.四条边长都确定的四边形,当内角的大小发生变化时,其形状也随之改变.如图,改变正方形ABCD的内角,使正方形ABCD变为菱形ABC'D',如果∠DAD'=30°,那么菱形ABC'D'与正方形ABCD的面积之比是( )
A.
B.
C.
D. 1
9.二次函数y=ax2+bx的图象如图所示,则一次函数y=x+b的图象一定不经过( )
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限
10.如图,在平面直角坐标系中,正方形ABCD的中心位于原点O处,AB=4,BC⊥x轴于点E,F为CE的中点.射线l的端点为O,将射线l从与OF重合的位置开始绕点O逆时针旋转,每次旋转45°,则第2025次旋转结束时,射线l与正方形ABCD的边的交点坐标为( )
A. (-1,2)
B. (1,2)
C.
D.
二、填空题:本题共5小题,每小题3分,共15分。
11.计算的结果为______.
12.中华文明源远流长,旅游资源非常丰富,“五一”期间,小娄和小金两人准备从开封、洛阳、南京、杭州四个历史古城中各选择一个景点旅游,他们通过抽签的方式确定景点,那么他们两人恰好能抽到同一景点的概率是______.
13.若关于x的一元二次方程x2-4x+2k=0有两个不相等实数根,则k的取值范围是______.
14.如图所示是某同学“抖空竹”的一个瞬间.已知绳子ACDB分别与空竹⊙O相切于点C,D,且AC=BD,连接左右两个绳柄A,B,AB经过圆心O,分别交⊙O于点M,N,经测量OM=AM=4,则图中阴影部分的周长为______.
15.如图,在△ABC中,AB=AC,∠BAC=90°,AD⊥BC于点D,点E在直线AD上运动,取AC的中点Q,连接QE,CE,当△QCE的周长最小,且最小值为时,△QCE的面积为______.
三、解答题:本题共8小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.(本小题10分)
(1)计算:+(2025-π)0-4-1;
(2)化简求值:,其中x=3.
17.(本小题9分)
随着自然语言处理、机器学习、深度学习等技术的不断进步,AI聊天机器人的智能化水平显著提高,能够更准确地理解用户意图并给出相应回答.预计2025年,我国对话机器人行业市场规模将达到98.5亿元.有关人员开展了对A,B两款AI聊天机器人的使用满意度的评分调查,并从中各随机抽取20份数据,进行整理、描述和分析(评分分数用x表示,满分100分,分为四个等级:甲:不满意x<70;乙:比较满意70≤x<80;丙:满意80≤x<90;丁:非常满意90≤x≤100).下面给出了部分信息.
抽取的对A款AI聊天机器人的评分数据中丙、丁两组的数据是:
82,85,87,87,87,87,87,87,89,93,93,97.
抽取的对B款AI聊天机器人的评分数据中丙、丁两组的数据一样多,丙组的数据是:
81,83,83,85,87,88,88,88.
数据显示A款AI聊天机器人的评分数据中甲组数据占15%,乙组数据为a个.B款AI聊天机器人的评分数据中甲组数据占5%.
AI聊天机器人 平均数 中位数 众数
A 86 86 c
B 86 b 90
根据以上信息,解答下列问题.
(1)a=______,b=______,c=______.
(2)根据以上数据,你认为哪款AI聊天机器人更受用户喜爱?请说明理由(写出一条理由即可).
(3)在此次调查中,有400人对甲款AI聊天机器人进行评分,300人对B款AI聊天机器人进行评分.请通过计算,估计此次调查中对AI聊天机器人不满意的共有多少人.
18.(本小题9分)
研学实践:如图1所示的建筑物是一座具有现代风格的文化地标,某数学小组利用航模搭载的3D扫描仪采集建筑物的相关数据.如图2,点A是建筑物顶部一点,AB的长表示点A到水平地面的距离.航模从建筑物前水平地面的点M处竖直上升,飞行至距离地面22米的点C处时,测得点A的仰角∠ACD=11.3°;然后沿CN方向继续飞行,飞行方向与水平线的夹角∠NCD=45°,当到达点A正上方的点E处时,测得AE=9米.已知图中各点均在同一竖直平面内,E,A,B三点在同一直线上.请根据上述数据,计算建筑物顶部点A到地面的距离AB的长(结果精确到1米.参考数据:sin11.3°≈0.196,cos11.3°≈0.981,tan11.3°≈0.200).
19.(本小题9分)
如图,在 ABCD中,已知A(-2,0)、B(2,0)、D(0,3),一个反比例函数的图象经过点C.
(1)求点C的坐标和该反比例函数的表达式;
(2)将 ABCD向上平移m个单位长度,再向右也平移m位长度,得到□A′B′C′D′.若此时点D′恰好落在反比例函数的图象上,求m满足的表达式;
(3)若将 ABCD沿直线CD翻折180°,得到口A″B″CD,则点B″是否在反比例函数的图象上?为什么?
20.(本小题9分)
如图,在Rt△ABC中,∠C=90°.
(1)尺规作图:作⊙O,使得圆心O在边AB上,⊙O过点B且与边AC相切于点D,交AB于点E(请保留作图痕迹,标明相应的字母,不写作法);
(2)在(1)的条件下,若AB=16,AD=8,求⊙O的半径.
(3)在(1)的条件下,求证:∠BOD=2∠BDC.
21.(本小题9分)
据灯塔专业版数据,截止2025年2月18日,《哪吒之魔童闹海》总票房达123.2亿元,登顶全球动画电影票房榜,并创造了全球单一电影市场最高票房纪录.该片来源于哪吒闹海的传统故事,但又重塑了全新的“魔童”哪吒形象:表面吊儿郎当,实则勇敢坚毅.为满足儿童对哪吒的喜爱,某玩具店购进了A、B两种哪吒玩偶.已知A种哪吒玩偶每个的进价为40元,售价为56元;B种哪吒玩偶每个的进价为30元,售价为45元.
(1)第一次店家用1100元钱购进了A,B两款哪吒玩偶共30个,求两款玩偶各购进多少个.
(2)第二次进货时,规定A款玩偶进货数量不得超过B款玩偶进货数量的一半,店家计划购进两款哪吒玩偶共30个,应如何设计进货方案才能获得最大利润,最大利润是多少?
22.(本小题10分)
为了增加趣味性,万岁山旅游城把传统的抛绣球项目进行改良,他们定制了一种器械,类似中国古代一种投石器,为了解发射平台高度对绣球飞行轨迹的影响,我们可以设定不同的发射平台高度,并分别记录绣球在不同水平距离上的飞行高度.分析不同发射平台高度下绣球的飞行轨迹.通过比较不同高度下绣球的飞行高度和飞行距离,我们可以得出发射平台高度对绣球飞行轨迹的具体影响.从而有目的地调整发射高度,通过实验发现绣球运动轨迹是抛物线的一部分,并且在离发射点水平距离18米处达到距地面最大高度18米;在离发射点水平距离6米处,距地面高度10米.
问题解决:
任务1:确定函数表达式.设绣球离发射点水平距离为x,距地面高度为y.求出y关于x的函数表达式;
任务2:探究飞行距离,当绣球从地面发出到落地(高度为0m)时,飞行的水平距离是多少;
任务3:如图,工作人员在水平地面上设置一个高度可以变化的发射平台PQ,当弹射口高度变化时,绣球被弹出后的飞行轨迹形状不变,可视为抛物线上下平移得到,点P,A,B在一条直线上,已知AP=37m,AB=1m,游客小李站在线段AB(包括点A,B)上,为了确保他能抢到绣球,请直接写出发射台PQ的变化范围:______.
23.(本小题10分)
(1)在数学活动课上,老师出示了这样一个问题;如图1,已知正方形ABCD,正方形CEFG.将正方形CEFG绕点C旋转,连接BE,DG,则BE与DG的数量关系为______;
(2)创新小组受到启发,将背景图形由正方形改为矩形继续进行探究,如图2,在矩形ABCD和矩形DEFG中,AD=2DE,AB=2DG,AD=DG,将矩形DEFG绕点D旋转,直线AE,CG交于点P,AE与CG有怎样的数量关系?请你给出证明.
(3)善思小组受此启发,举一反三,提出新问题:如图3,四边形ABCD是矩形,AB=2,BC=4,点E是AD边上的一个动点,以CE为边在CE的右侧作矩形CEFG,且CG:CE=1:2,连接BG,DG,BE,则的最小值是______.
1.
解:∵向东走2km记做“+2km”,
∴向西走1km应记做:-1km.
故选:B.
2.
解:9700万=97000000=9.7×107.
故选:C.
3.
解:A.∵(a3)n+1=a3n+3,∴此选项的计算错误,故此选项不符合题意;
B.∵(-a2)3 a6=(-a6) a6=-a12,∴此选项的计算错误,故此选项不符合题意;
C.∵a8m a8m=a16m,∴此选项的计算错误,故此选项不符合题意;
D.∵(-m) (-m)4=(-m)5=-m5,∴此选项的计算正确,故此选项符合题意;
故选:D.
4.
解:根据题意可知,立体图形的主视图为:第一层是三个小正方形,第二层右边是一个小正方形.
故选:D.
5.
解:两方程相减得x-y=-2,
故选:B.
6.
解:∵∠BAC=90°,∠B=50°,
∴∠C=40°.
∵△ADB与△ADB'关于直线AD对称,点B的对称点是点B',
∴∠AB'B=∠B=50°,
∴∠CAB'=∠AB'B-∠C=50°-40°=10°.
故选:A.
7.
解:由统计图可知,两园样本数据的中位数均在第3组,故①正确;
甲园的众数在第2组,乙园的众数在第3组,故②结论错误;
两园样本数据的最大数与最小数的差不一定相等,故③结论错误;
故选:A.
8.
解:过D'作D'M⊥AB于M,如图所示:
则∠D'MA=90°,
∵四边形ABCD是正方形,
∴正方形ABCD的面积=AB2,AB=AD,∠BAD=90°,
∵∠DAD′=30°,
∴∠D'AM=90°-30°=60°,
∴∠AD'M=30°,
∴AM=AD',D'M=AM=AD',
∵四边形ABC′D′是菱形,
∴AB=AD'=AD,菱形ABCD的面积=AB×D'M=AB2,
∴菱形ABC′D′与正方形ABCD的面积之比==,
故选:A.
9.
解:由图象开口向下可知a<0,b>0,
∴一次函数y=x+b的图象经过第一、二、三象限,不经过第四象限.
故选:D.
10.
解:把OF绕F顺时针旋转90°得到线段FH,连接OH交CD于P,过H作HG⊥BC交BC延长线与G,
由条件可知C(2,2),D(-2,2),F(2,1),∠OEF=90°,
∴OE=2,EF=1,
∵把OF绕F顺时针旋转90°得到线段FH,HG⊥BC,
∴OF=FH,∠OEF=∠OFH=∠G=90°,
∴∠OFE=∠FHG=90°-∠HFG,
∴△OEF≌△FGH(AAS),
∴OE=FG=2,EF=GH=1,
∴EG=EF+FG=3,
∴H(1,3),
∴正比例函数OH解析式为y=3x,
当y=3x=2时,,
∴,
由条件可知:第一次旋转结束时射线l与正方形ABCD的边的交点,
∵360°÷45°=8,
∴每8次一个循环,
∵2025÷8=253 1,
∴第2025次旋转结束时,射线l与正方形ABCD的边的交点与第一次旋转结束时射线l与正方形ABCD的边的交点是同一个点,即,
故选:D.
11.
解:
=11-1-1
=9,
故答案为:9.
12.
解:将开封、洛阳、南京、杭州分别记为A,B,C,D,
列表如下:
A B C D
A (A,A) (A,B) (A,C) (A,D)
B (B,A) (B,B) (B,C) (B,D)
C (C,A) (C,B) (C,C) (C,D)
D (D,A) (D,B) (D,C) (D,D)
共有16种等可能的结果,其中他们两人恰好能抽到同一景点的结果有4种,
∴他们两人恰好能抽到同一景点的概率为.
故答案为:.
13.
解:∵关于x的一元二次方程x2-4x+2k=0有两个不相等的实数根,
∴△=16-4×2k>0.
解得k<2.
故答案为:k<2.
14.
解:连接OC、OD,
∵绳子ACDB分别与空竹⊙O相切于点C,D,
∴OC⊥AC,OD⊥BD,
∴∠OCA=∠ODB=90°,
∵OM=AM=4,
∴OC=OM=4,
∴cos∠AOC===,
∴∠AOC=60°,
∴AC=OC=4,
∵BD=AC=4,
∴tan∠BOD===,
∴∠BOD=60°,
∴OB=2OD=8,
∴∠COD=60°,
∴弧CD的长度==π,
∴图中阴影部分的周长=AC+的长+BD+AB=4+3π+4+8+8=8+16+3π.
故答案为:8+16+3π.
15.
解:如图,连接BQ交AD于E,
∵AB=AC,∠BAC=90°,AD⊥BC于D,
∴AD垂直平分BC,
∴BE=CE,
∴CE+QE=BE+QE≤BE,
∵Q是AC的中点,
∴CQ是定值,当B、Q、E共线时,CE+QE=BQ最小,即△QOE 的周长最小,
作QH⊥BC于H,设CQ=x,
∵AD⊥BC,
∴QH∥AD,
∵Q是AC的中点,∠ACB=45°,x,DH=x,
∴,
∴,
在Rt△BQH中,,
∵△QCE的周长最小值为CE+QE+CQ=BQ+CQ=2,
∴,
解得x=2,
∴,
∵QH∥AD,
∴△BED∽△BQH,
∴,
∴,
∴×.
故答案为:.
16.
(1)原式=
=
=.
(2)
=
=
=-1-x.
当x=3时,
原式=-4.
17.
由题意得:A款AI聊天机器人的评分数据中甲组数据为20×15%=3(个),
∴a=20-3-12=5;
∵抽取的对B款AI聊天机器人的评分数据中丙、丁两组的数据一样多,丙组的数据有8个,
∴丁组的数据有8个,
∴把B款的评分数据从小到大排列,排在中间的两个数是88、88,
∴b==88,
在A款的评分数据中,87出现的次数最多,
∴c=87;
故答案为:5,88,87;
(2)B款AI聊天机器人更受用户喜爱,理由如下:
∵两款AI聊天机器人的评分数据的平均数相同,但B款评分数据的中位数比A款的中位数高,
∴.B款AI聊天机器人更受用户喜爱(合理即可);
(3)400×15%+300×5%=75(人).
答:此次调查中对AI聊天机器人不满意的人数约为75人.
18.
解:延长CD交AB于点H,
由题意得:CH⊥BE,CM=BH=22米,
设AH=x米,
∵AE=9米,
∴EH=AE+AH=(x+9)米,
在Rt△CEH中,∠NCD=45°,
∴CH==(x+9)米,
在Rt△ACH中,∠ACD=11.3°,
∴tan11.3°==≈0.2,
解得:x=2.25,
∴AH=2.25米,
∴AB=BH+AH=22+2.25≈24(米),
答:AB的高约为24米.
19.
(1)在 ABCD中,
∵A(-2,0)、B(2,0)、D(0,3),
∴点C的坐标为(4,3),
∵反比例函数的图象经过点C.
∴k=4×3=12,
∴反比例函数的表达式为:y=;
(2)∵将 ABCD向上平移m个单位长度,再向右也平移m位长度,得到□A′B′C′D′,D(0,3),
∴点D′的坐标为(m,3+m),
∵点D′恰好落在反比例函数的图象上,
∴m(3+m)=12,
∴m满足的表达式为:m2+3m=12;
(3)点B″在反比例函数的图象上.
理由:∵将 ABCD沿直线CD翻折180°,得到 A″B″CD,A(-2,0)、B(2,0)、D(0,3),
∴点B″的坐标为(2,6),
∵2×6=12,
∴点B″在反比例函数的图象上.
20.
(1)解:1.作∠ABC的平分线BD,交AC于点D,
2.过点D作DO⊥AC于点D,交AB于点O,
3.以点O为圆心,OD为半径画圆,交AB于点E,如图,
则⊙O即为所求作.
(2)解:连接OD,如图,
∵AC与⊙O相切,
∴OD⊥AC,
∴∠ODA=90°,
设OD=OB=x,
∴AO=16-x.
在Rt△ADO中,
∵AO2=AD2+OD2,
∴82+x2=(16-x)2,
∴x=6.
∴⊙O的半径为6.
(3)证明:连接BD,如图,
设∠ODB=m°,
∵OD=OB,
∴∠ODB=∠OBD=m°.
∴∠BOD=180°-2m°=2(90°-m°),
∵AC为⊙O的切线,
∴OD⊥AC.
∴∠BDC=∠ODC-∠ODB=90°-m°,
∴∠BOD=2∠BDC.
21.
(1)由题意,设A款玩偶购进x个,则B款玩偶购进(30- x)个,
∴40x+30(30-x)=1100,
∴x=20.
∴30-20=10(个).
答:A款哪吒玩偶购进20个,B款哪吒玩偶购进10个.
(2)由题意,设A款哪吒玩偶购进a个,则B款哪吒玩偶购进(30- a)个,获利 y元,
∴y=(56-40)a+(45-30)(30-a)=a+450.
∵A款哪吒玩偶进货数量不得超过B款哪吒玩偶进货数量的一半,
∴,
∴a≤10.
∵y=a+450,
∴k=1>0,
∴y随a的增大而增大.
∴a=10时y晶大=460.
∴B款哪吒玩偶购进30-10=20(个).
答:按照A款玩偶购进10个,B款玩偶购进20个的方案进货才能获得最大利润,最大利润是460元.
22.
解:任务1:依题意,得抛物线的顶点坐标为(18,18),
设抛物线解析式为y=a(x-18)2+18,
把(6,10)代入解析式得:10=a(6-18)2+18.
解得,
∴抛物线解析式为;
任务2:令y=0,
则,
解得x1=36,x=0(舍),
答:水平距离为36m;
任务3:设抛物线向上平移m个单位,则平移后的抛物线解析式为y=-(x-18)2+18+m,
∵OA=37m,AB=1m,
∴当抛物线经过(37,0)时,0=-(37-18)2+18+m,
解得m=;
当抛物线经过(38,0)时,0=-(38-18)2+18+m,
解得m=,
∴出发射台PQ的变化范围为:≤PQ≤,
故答案为:≤PQ≤.
23.
(1)∵正方形ABCD,
∴∠BCD=90°,CD=CB,
∵四边形ECGF是正方形,
∴∠ECG=90°,CG=CE,
∴∠ECG=∠BCD=90°,
∴∠BCE=∠DCG,
在△BCE和△DCG中,
,
∴△DCG≌△BCE(SAS),
∴DG=BE,
故答案为:BE=DG;
(2)CG=2AE,理由如下:
在矩形ABCD和矩形DEFG中,
∠GDE=∠ADC=90°,
∴∠ADC+∠ADG=∠GDE+∠ADG,
∴∠GDC=∠ADE.
又∵AD=2DE,AB=2DG,AD=DG,
∴,
∴△CDG∽△ADE,
∴.
∴CG=2AE;
(3)∵四边形ECGF、四边形ABCD都是矩形,
∴CD=AB=2,AD=BC=4,∠ECG=∠BCD=90°,
∴∠DCG=∠BCE,
∵CD:CB=2:4=1:2,CG:CE=1:2,
∴CD:CB=CG:CE,
∵∠DCG=∠BCE,
∴△DCG∽△BCE,
∴∠BEC=∠DGC,==,
∴DG=BE,
作EN⊥BC于N,GM⊥BC交BC的延长线于M,如图3,
∵∠FNC=∠CMG=∠ECG=90°,
∴∠FCN+∠GCM=∠FCN+∠CEN=90°,
∴∠GCM=∠CEN,
∴△ECN∽△CGM,
∴==2,
∵EN=AB=2,
∴CM=1,
∴点G的运动轨迹是直线MG,
作点D关于直线MG的对称点G′,连接BG′交MG于G,此时BG+GD的值最小,最小值为BG′,
∵DG=BE,
∴BG+BE=BG+DG,
∴BG+BE的最小值就是(BG+DG)的最小值,
∵BG′==2,
∴BG+BE的最小值为2.
故答案为:2.
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.负数的概念最早出现在《九章算术》中,把向东走2km记做“+2km”,向西走1km应记做( )
A. -2km B. -1km C. 1km D. +2km
2.DeepSeek,全称杭州深度求索人工智能基础技术研究有限公司,截至2025年2月9日,Deep-Seek的累计下载量已超过1.1亿次,周活跃用户规模高达9700万.其中9700万用科学记数法表示为( )
A. 9700×104 B. 97×106 C. 9.7×107 D. 0.97×108
3.下列计算正确的是( )
A. (a3)n+1=a3n+1 B. (-a2)3 a6=a12
C. a8m a8m=2a16m D. (-m)(-m)4=-m5
4.如图是一个由5个相同的正方体组成的立体图形,它的主视图是( )
A.
B.
C.
D.
5.已知二元一次方程组,则x-y的值为( )
A. 2 B. -2 C. 4 D. -4
6.如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB′关于直线AD对称,点B的对称点是点B′,则∠CAB′的度数为( )
A. 10° B. 20° C. 30° D. 40°
7.从两块柑橘园采摘的柑橘中各随机选取200个.在技术人员指导下,测量每个柑橘的直径,作为样本数据.柑橘直径用x(单位:cm)表示,整理所收集样本数据,并绘制甲、乙两园样本数据的频数分布直方图,部分信息如下:
下列结论一定正确的是( )
①两园样本数据的中位数均在第3组;
②两园样本数据的众数均在第3组;
③两园样本数据的最大数与最小数的差相等.
A. ① B. ①② C. ①③ D. ①②③
8.四边形不具有稳定性.四条边长都确定的四边形,当内角的大小发生变化时,其形状也随之改变.如图,改变正方形ABCD的内角,使正方形ABCD变为菱形ABC'D',如果∠DAD'=30°,那么菱形ABC'D'与正方形ABCD的面积之比是( )
A.
B.
C.
D. 1
9.二次函数y=ax2+bx的图象如图所示,则一次函数y=x+b的图象一定不经过( )
A. 第一象限
B. 第二象限
C. 第三象限
D. 第四象限
10.如图,在平面直角坐标系中,正方形ABCD的中心位于原点O处,AB=4,BC⊥x轴于点E,F为CE的中点.射线l的端点为O,将射线l从与OF重合的位置开始绕点O逆时针旋转,每次旋转45°,则第2025次旋转结束时,射线l与正方形ABCD的边的交点坐标为( )
A. (-1,2)
B. (1,2)
C.
D.
二、填空题:本题共5小题,每小题3分,共15分。
11.计算的结果为______.
12.中华文明源远流长,旅游资源非常丰富,“五一”期间,小娄和小金两人准备从开封、洛阳、南京、杭州四个历史古城中各选择一个景点旅游,他们通过抽签的方式确定景点,那么他们两人恰好能抽到同一景点的概率是______.
13.若关于x的一元二次方程x2-4x+2k=0有两个不相等实数根,则k的取值范围是______.
14.如图所示是某同学“抖空竹”的一个瞬间.已知绳子ACDB分别与空竹⊙O相切于点C,D,且AC=BD,连接左右两个绳柄A,B,AB经过圆心O,分别交⊙O于点M,N,经测量OM=AM=4,则图中阴影部分的周长为______.
15.如图,在△ABC中,AB=AC,∠BAC=90°,AD⊥BC于点D,点E在直线AD上运动,取AC的中点Q,连接QE,CE,当△QCE的周长最小,且最小值为时,△QCE的面积为______.
三、解答题:本题共8小题,共75分。解答应写出文字说明,证明过程或演算步骤。
16.(本小题10分)
(1)计算:+(2025-π)0-4-1;
(2)化简求值:,其中x=3.
17.(本小题9分)
随着自然语言处理、机器学习、深度学习等技术的不断进步,AI聊天机器人的智能化水平显著提高,能够更准确地理解用户意图并给出相应回答.预计2025年,我国对话机器人行业市场规模将达到98.5亿元.有关人员开展了对A,B两款AI聊天机器人的使用满意度的评分调查,并从中各随机抽取20份数据,进行整理、描述和分析(评分分数用x表示,满分100分,分为四个等级:甲:不满意x<70;乙:比较满意70≤x<80;丙:满意80≤x<90;丁:非常满意90≤x≤100).下面给出了部分信息.
抽取的对A款AI聊天机器人的评分数据中丙、丁两组的数据是:
82,85,87,87,87,87,87,87,89,93,93,97.
抽取的对B款AI聊天机器人的评分数据中丙、丁两组的数据一样多,丙组的数据是:
81,83,83,85,87,88,88,88.
数据显示A款AI聊天机器人的评分数据中甲组数据占15%,乙组数据为a个.B款AI聊天机器人的评分数据中甲组数据占5%.
AI聊天机器人 平均数 中位数 众数
A 86 86 c
B 86 b 90
根据以上信息,解答下列问题.
(1)a=______,b=______,c=______.
(2)根据以上数据,你认为哪款AI聊天机器人更受用户喜爱?请说明理由(写出一条理由即可).
(3)在此次调查中,有400人对甲款AI聊天机器人进行评分,300人对B款AI聊天机器人进行评分.请通过计算,估计此次调查中对AI聊天机器人不满意的共有多少人.
18.(本小题9分)
研学实践:如图1所示的建筑物是一座具有现代风格的文化地标,某数学小组利用航模搭载的3D扫描仪采集建筑物的相关数据.如图2,点A是建筑物顶部一点,AB的长表示点A到水平地面的距离.航模从建筑物前水平地面的点M处竖直上升,飞行至距离地面22米的点C处时,测得点A的仰角∠ACD=11.3°;然后沿CN方向继续飞行,飞行方向与水平线的夹角∠NCD=45°,当到达点A正上方的点E处时,测得AE=9米.已知图中各点均在同一竖直平面内,E,A,B三点在同一直线上.请根据上述数据,计算建筑物顶部点A到地面的距离AB的长(结果精确到1米.参考数据:sin11.3°≈0.196,cos11.3°≈0.981,tan11.3°≈0.200).
19.(本小题9分)
如图,在 ABCD中,已知A(-2,0)、B(2,0)、D(0,3),一个反比例函数的图象经过点C.
(1)求点C的坐标和该反比例函数的表达式;
(2)将 ABCD向上平移m个单位长度,再向右也平移m位长度,得到□A′B′C′D′.若此时点D′恰好落在反比例函数的图象上,求m满足的表达式;
(3)若将 ABCD沿直线CD翻折180°,得到口A″B″CD,则点B″是否在反比例函数的图象上?为什么?
20.(本小题9分)
如图,在Rt△ABC中,∠C=90°.
(1)尺规作图:作⊙O,使得圆心O在边AB上,⊙O过点B且与边AC相切于点D,交AB于点E(请保留作图痕迹,标明相应的字母,不写作法);
(2)在(1)的条件下,若AB=16,AD=8,求⊙O的半径.
(3)在(1)的条件下,求证:∠BOD=2∠BDC.
21.(本小题9分)
据灯塔专业版数据,截止2025年2月18日,《哪吒之魔童闹海》总票房达123.2亿元,登顶全球动画电影票房榜,并创造了全球单一电影市场最高票房纪录.该片来源于哪吒闹海的传统故事,但又重塑了全新的“魔童”哪吒形象:表面吊儿郎当,实则勇敢坚毅.为满足儿童对哪吒的喜爱,某玩具店购进了A、B两种哪吒玩偶.已知A种哪吒玩偶每个的进价为40元,售价为56元;B种哪吒玩偶每个的进价为30元,售价为45元.
(1)第一次店家用1100元钱购进了A,B两款哪吒玩偶共30个,求两款玩偶各购进多少个.
(2)第二次进货时,规定A款玩偶进货数量不得超过B款玩偶进货数量的一半,店家计划购进两款哪吒玩偶共30个,应如何设计进货方案才能获得最大利润,最大利润是多少?
22.(本小题10分)
为了增加趣味性,万岁山旅游城把传统的抛绣球项目进行改良,他们定制了一种器械,类似中国古代一种投石器,为了解发射平台高度对绣球飞行轨迹的影响,我们可以设定不同的发射平台高度,并分别记录绣球在不同水平距离上的飞行高度.分析不同发射平台高度下绣球的飞行轨迹.通过比较不同高度下绣球的飞行高度和飞行距离,我们可以得出发射平台高度对绣球飞行轨迹的具体影响.从而有目的地调整发射高度,通过实验发现绣球运动轨迹是抛物线的一部分,并且在离发射点水平距离18米处达到距地面最大高度18米;在离发射点水平距离6米处,距地面高度10米.
问题解决:
任务1:确定函数表达式.设绣球离发射点水平距离为x,距地面高度为y.求出y关于x的函数表达式;
任务2:探究飞行距离,当绣球从地面发出到落地(高度为0m)时,飞行的水平距离是多少;
任务3:如图,工作人员在水平地面上设置一个高度可以变化的发射平台PQ,当弹射口高度变化时,绣球被弹出后的飞行轨迹形状不变,可视为抛物线上下平移得到,点P,A,B在一条直线上,已知AP=37m,AB=1m,游客小李站在线段AB(包括点A,B)上,为了确保他能抢到绣球,请直接写出发射台PQ的变化范围:______.
23.(本小题10分)
(1)在数学活动课上,老师出示了这样一个问题;如图1,已知正方形ABCD,正方形CEFG.将正方形CEFG绕点C旋转,连接BE,DG,则BE与DG的数量关系为______;
(2)创新小组受到启发,将背景图形由正方形改为矩形继续进行探究,如图2,在矩形ABCD和矩形DEFG中,AD=2DE,AB=2DG,AD=DG,将矩形DEFG绕点D旋转,直线AE,CG交于点P,AE与CG有怎样的数量关系?请你给出证明.
(3)善思小组受此启发,举一反三,提出新问题:如图3,四边形ABCD是矩形,AB=2,BC=4,点E是AD边上的一个动点,以CE为边在CE的右侧作矩形CEFG,且CG:CE=1:2,连接BG,DG,BE,则的最小值是______.
1.
解:∵向东走2km记做“+2km”,
∴向西走1km应记做:-1km.
故选:B.
2.
解:9700万=97000000=9.7×107.
故选:C.
3.
解:A.∵(a3)n+1=a3n+3,∴此选项的计算错误,故此选项不符合题意;
B.∵(-a2)3 a6=(-a6) a6=-a12,∴此选项的计算错误,故此选项不符合题意;
C.∵a8m a8m=a16m,∴此选项的计算错误,故此选项不符合题意;
D.∵(-m) (-m)4=(-m)5=-m5,∴此选项的计算正确,故此选项符合题意;
故选:D.
4.
解:根据题意可知,立体图形的主视图为:第一层是三个小正方形,第二层右边是一个小正方形.
故选:D.
5.
解:两方程相减得x-y=-2,
故选:B.
6.
解:∵∠BAC=90°,∠B=50°,
∴∠C=40°.
∵△ADB与△ADB'关于直线AD对称,点B的对称点是点B',
∴∠AB'B=∠B=50°,
∴∠CAB'=∠AB'B-∠C=50°-40°=10°.
故选:A.
7.
解:由统计图可知,两园样本数据的中位数均在第3组,故①正确;
甲园的众数在第2组,乙园的众数在第3组,故②结论错误;
两园样本数据的最大数与最小数的差不一定相等,故③结论错误;
故选:A.
8.
解:过D'作D'M⊥AB于M,如图所示:
则∠D'MA=90°,
∵四边形ABCD是正方形,
∴正方形ABCD的面积=AB2,AB=AD,∠BAD=90°,
∵∠DAD′=30°,
∴∠D'AM=90°-30°=60°,
∴∠AD'M=30°,
∴AM=AD',D'M=AM=AD',
∵四边形ABC′D′是菱形,
∴AB=AD'=AD,菱形ABCD的面积=AB×D'M=AB2,
∴菱形ABC′D′与正方形ABCD的面积之比==,
故选:A.
9.
解:由图象开口向下可知a<0,b>0,
∴一次函数y=x+b的图象经过第一、二、三象限,不经过第四象限.
故选:D.
10.
解:把OF绕F顺时针旋转90°得到线段FH,连接OH交CD于P,过H作HG⊥BC交BC延长线与G,
由条件可知C(2,2),D(-2,2),F(2,1),∠OEF=90°,
∴OE=2,EF=1,
∵把OF绕F顺时针旋转90°得到线段FH,HG⊥BC,
∴OF=FH,∠OEF=∠OFH=∠G=90°,
∴∠OFE=∠FHG=90°-∠HFG,
∴△OEF≌△FGH(AAS),
∴OE=FG=2,EF=GH=1,
∴EG=EF+FG=3,
∴H(1,3),
∴正比例函数OH解析式为y=3x,
当y=3x=2时,,
∴,
由条件可知:第一次旋转结束时射线l与正方形ABCD的边的交点,
∵360°÷45°=8,
∴每8次一个循环,
∵2025÷8=253 1,
∴第2025次旋转结束时,射线l与正方形ABCD的边的交点与第一次旋转结束时射线l与正方形ABCD的边的交点是同一个点,即,
故选:D.
11.
解:
=11-1-1
=9,
故答案为:9.
12.
解:将开封、洛阳、南京、杭州分别记为A,B,C,D,
列表如下:
A B C D
A (A,A) (A,B) (A,C) (A,D)
B (B,A) (B,B) (B,C) (B,D)
C (C,A) (C,B) (C,C) (C,D)
D (D,A) (D,B) (D,C) (D,D)
共有16种等可能的结果,其中他们两人恰好能抽到同一景点的结果有4种,
∴他们两人恰好能抽到同一景点的概率为.
故答案为:.
13.
解:∵关于x的一元二次方程x2-4x+2k=0有两个不相等的实数根,
∴△=16-4×2k>0.
解得k<2.
故答案为:k<2.
14.
解:连接OC、OD,
∵绳子ACDB分别与空竹⊙O相切于点C,D,
∴OC⊥AC,OD⊥BD,
∴∠OCA=∠ODB=90°,
∵OM=AM=4,
∴OC=OM=4,
∴cos∠AOC===,
∴∠AOC=60°,
∴AC=OC=4,
∵BD=AC=4,
∴tan∠BOD===,
∴∠BOD=60°,
∴OB=2OD=8,
∴∠COD=60°,
∴弧CD的长度==π,
∴图中阴影部分的周长=AC+的长+BD+AB=4+3π+4+8+8=8+16+3π.
故答案为:8+16+3π.
15.
解:如图,连接BQ交AD于E,
∵AB=AC,∠BAC=90°,AD⊥BC于D,
∴AD垂直平分BC,
∴BE=CE,
∴CE+QE=BE+QE≤BE,
∵Q是AC的中点,
∴CQ是定值,当B、Q、E共线时,CE+QE=BQ最小,即△QOE 的周长最小,
作QH⊥BC于H,设CQ=x,
∵AD⊥BC,
∴QH∥AD,
∵Q是AC的中点,∠ACB=45°,x,DH=x,
∴,
∴,
在Rt△BQH中,,
∵△QCE的周长最小值为CE+QE+CQ=BQ+CQ=2,
∴,
解得x=2,
∴,
∵QH∥AD,
∴△BED∽△BQH,
∴,
∴,
∴×.
故答案为:.
16.
(1)原式=
=
=.
(2)
=
=
=-1-x.
当x=3时,
原式=-4.
17.
由题意得:A款AI聊天机器人的评分数据中甲组数据为20×15%=3(个),
∴a=20-3-12=5;
∵抽取的对B款AI聊天机器人的评分数据中丙、丁两组的数据一样多,丙组的数据有8个,
∴丁组的数据有8个,
∴把B款的评分数据从小到大排列,排在中间的两个数是88、88,
∴b==88,
在A款的评分数据中,87出现的次数最多,
∴c=87;
故答案为:5,88,87;
(2)B款AI聊天机器人更受用户喜爱,理由如下:
∵两款AI聊天机器人的评分数据的平均数相同,但B款评分数据的中位数比A款的中位数高,
∴.B款AI聊天机器人更受用户喜爱(合理即可);
(3)400×15%+300×5%=75(人).
答:此次调查中对AI聊天机器人不满意的人数约为75人.
18.
解:延长CD交AB于点H,
由题意得:CH⊥BE,CM=BH=22米,
设AH=x米,
∵AE=9米,
∴EH=AE+AH=(x+9)米,
在Rt△CEH中,∠NCD=45°,
∴CH==(x+9)米,
在Rt△ACH中,∠ACD=11.3°,
∴tan11.3°==≈0.2,
解得:x=2.25,
∴AH=2.25米,
∴AB=BH+AH=22+2.25≈24(米),
答:AB的高约为24米.
19.
(1)在 ABCD中,
∵A(-2,0)、B(2,0)、D(0,3),
∴点C的坐标为(4,3),
∵反比例函数的图象经过点C.
∴k=4×3=12,
∴反比例函数的表达式为:y=;
(2)∵将 ABCD向上平移m个单位长度,再向右也平移m位长度,得到□A′B′C′D′,D(0,3),
∴点D′的坐标为(m,3+m),
∵点D′恰好落在反比例函数的图象上,
∴m(3+m)=12,
∴m满足的表达式为:m2+3m=12;
(3)点B″在反比例函数的图象上.
理由:∵将 ABCD沿直线CD翻折180°,得到 A″B″CD,A(-2,0)、B(2,0)、D(0,3),
∴点B″的坐标为(2,6),
∵2×6=12,
∴点B″在反比例函数的图象上.
20.
(1)解:1.作∠ABC的平分线BD,交AC于点D,
2.过点D作DO⊥AC于点D,交AB于点O,
3.以点O为圆心,OD为半径画圆,交AB于点E,如图,
则⊙O即为所求作.
(2)解:连接OD,如图,
∵AC与⊙O相切,
∴OD⊥AC,
∴∠ODA=90°,
设OD=OB=x,
∴AO=16-x.
在Rt△ADO中,
∵AO2=AD2+OD2,
∴82+x2=(16-x)2,
∴x=6.
∴⊙O的半径为6.
(3)证明:连接BD,如图,
设∠ODB=m°,
∵OD=OB,
∴∠ODB=∠OBD=m°.
∴∠BOD=180°-2m°=2(90°-m°),
∵AC为⊙O的切线,
∴OD⊥AC.
∴∠BDC=∠ODC-∠ODB=90°-m°,
∴∠BOD=2∠BDC.
21.
(1)由题意,设A款玩偶购进x个,则B款玩偶购进(30- x)个,
∴40x+30(30-x)=1100,
∴x=20.
∴30-20=10(个).
答:A款哪吒玩偶购进20个,B款哪吒玩偶购进10个.
(2)由题意,设A款哪吒玩偶购进a个,则B款哪吒玩偶购进(30- a)个,获利 y元,
∴y=(56-40)a+(45-30)(30-a)=a+450.
∵A款哪吒玩偶进货数量不得超过B款哪吒玩偶进货数量的一半,
∴,
∴a≤10.
∵y=a+450,
∴k=1>0,
∴y随a的增大而增大.
∴a=10时y晶大=460.
∴B款哪吒玩偶购进30-10=20(个).
答:按照A款玩偶购进10个,B款玩偶购进20个的方案进货才能获得最大利润,最大利润是460元.
22.
解:任务1:依题意,得抛物线的顶点坐标为(18,18),
设抛物线解析式为y=a(x-18)2+18,
把(6,10)代入解析式得:10=a(6-18)2+18.
解得,
∴抛物线解析式为;
任务2:令y=0,
则,
解得x1=36,x=0(舍),
答:水平距离为36m;
任务3:设抛物线向上平移m个单位,则平移后的抛物线解析式为y=-(x-18)2+18+m,
∵OA=37m,AB=1m,
∴当抛物线经过(37,0)时,0=-(37-18)2+18+m,
解得m=;
当抛物线经过(38,0)时,0=-(38-18)2+18+m,
解得m=,
∴出发射台PQ的变化范围为:≤PQ≤,
故答案为:≤PQ≤.
23.
(1)∵正方形ABCD,
∴∠BCD=90°,CD=CB,
∵四边形ECGF是正方形,
∴∠ECG=90°,CG=CE,
∴∠ECG=∠BCD=90°,
∴∠BCE=∠DCG,
在△BCE和△DCG中,
,
∴△DCG≌△BCE(SAS),
∴DG=BE,
故答案为:BE=DG;
(2)CG=2AE,理由如下:
在矩形ABCD和矩形DEFG中,
∠GDE=∠ADC=90°,
∴∠ADC+∠ADG=∠GDE+∠ADG,
∴∠GDC=∠ADE.
又∵AD=2DE,AB=2DG,AD=DG,
∴,
∴△CDG∽△ADE,
∴.
∴CG=2AE;
(3)∵四边形ECGF、四边形ABCD都是矩形,
∴CD=AB=2,AD=BC=4,∠ECG=∠BCD=90°,
∴∠DCG=∠BCE,
∵CD:CB=2:4=1:2,CG:CE=1:2,
∴CD:CB=CG:CE,
∵∠DCG=∠BCE,
∴△DCG∽△BCE,
∴∠BEC=∠DGC,==,
∴DG=BE,
作EN⊥BC于N,GM⊥BC交BC的延长线于M,如图3,
∵∠FNC=∠CMG=∠ECG=90°,
∴∠FCN+∠GCM=∠FCN+∠CEN=90°,
∴∠GCM=∠CEN,
∴△ECN∽△CGM,
∴==2,
∵EN=AB=2,
∴CM=1,
∴点G的运动轨迹是直线MG,
作点D关于直线MG的对称点G′,连接BG′交MG于G,此时BG+GD的值最小,最小值为BG′,
∵DG=BE,
∴BG+BE=BG+DG,
∴BG+BE的最小值就是(BG+DG)的最小值,
∵BG′==2,
∴BG+BE的最小值为2.
故答案为:2.
同课章节目录
