广东省湛江市雷州市四校2025年九年级下学期中考三模数学试卷(含答案)
文档属性
| 名称 | 广东省湛江市雷州市四校2025年九年级下学期中考三模数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 00:00:00 | ||
图片预览




文档简介
2025年广东省湛江市雷州市九年级四校三模联考数学试题
一、单选题
1.下列实数是无理数的是( )
A.1 B. C. D.2024
2.珠海长隆海洋王国的鲸鲨馆水体量约为立方米,将用科学记数法表示正确的是( )
A. B. C. D.
3.2025年春晚的主题是“巳巳如意,生生不息”,如图为春晚主标识,巧妙组合的两个“巳”字象征中国传统的如意纹样,寓意双巳合璧,带来事事如意的吉祥.下列关于该标识的说法正确的是( )
A.是轴对称图形不是中心对称图形
B.是中心对称图形不是轴对称图形
C.既是轴对称图形又是中心对称图形
D.既不是轴对称图形也不是中心对称图形
4.下列计算正确的是( )
A. B.
C. D.
5.不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
6.如图,边长为1的小正方形网格中,⊙O的圆心在格点上,则∠AED的余弦值是( )
A. B.1 C. D.
7.下列说法错误的是( )
A.对角线垂直且互相平分的四边形是菱形 B.同圆或等圆中,同弧对应的圆周角相等
C.对角线相等的四边形是矩形 D.对角线垂直且相等的平行四边形是正方形
8.已知点都在反比例函数的图象上,则的大小关系是( )
A. B.
C. D.
9.如图,是的内接三角形,,则的度数为( )
A. B. C. D.
10.如图,在中(),,点,分别是,上的动点,连接,,点和关于对称,点和关于对称,且点,都在所在的直线上.已知,设,.下列代数式的值不变的是( )
A. B. C. D.
二、填空题
11.在函数中,自变量x的取值范围是 .
12.计算: .
13.甲、乙、丙三名男同学进行跳远测试,每人10次跳远成绩的平均数都是,方差分别是,则这三名同学跳远成绩最不稳定的是 .
14.若,则 .
15.如图,在矩形中,,点E,F分别在边,上,交于点G,若G是的中点,下列四个结论中:①;②;③;④,正确的是 (填序号即可)
三、解答题
16.计算:
17.如图,在中,分别以为圆心,以大于的长为半径画弧,两弧交于点,作直线分别交于点,交于点.
(1)填空:直线是的___________;
(2)求证:.
18.黄梅戏是“中国五大戏曲剧种”之一,也是安徽省的主要地方戏曲剧种.为激发学生对黄梅戏的热爱,某校举行黄梅戏演唱比赛,将全部参赛选手的成绩(满分为100分,得分为正整数且无满分,最低为75分)分成五组:A:,B:,C:,D:,E:,并绘制了如下频数分布直方图和扇形统计图,部分信息如下:
请根据以上信息,完成下列问题:
(1)填空:频数分布直方图中,________,扇形统计图中,圆心角________;
(2)A,B,C,D,E这五组数据的平均数分别为77,82,87,92,97,计算全部参赛选手成绩的平均分;
(3)在E组的选手中有男生1名,女生3名,学校打算从这4名选手中随机选取2名参加市级比赛,求恰好选中一名男生和一名女生的概率.
19.鲜桃刚上市,某水果店率先用1000元购进了一批鲜桃,前两天以高于进价的价格卖出;第三天水果店又用1000元购进了一批鲜桃,由于进价降低了,这一批鲜桃多购进.
(1)求水果店购进第一批鲜桃的数量;
(2)注意到市场上鲜桃数量逐渐增多,水果店主决定将剩余和新进鲜桃在原销售价的基础上,全部降价元(为整数)销售.实际销售过程中,平均每天销售量相对于前两天平均每天增加了,仅仅销售两天,剩下量不超过.
①求的值;
②若店主将剩余鲜桃以20元的价格全部卖完,求前后一共获利多少元.
20.综合与实践
问题背景:
如图为一汽车停车棚及它的侧面示意图,其棚顶的横截面可以看作是抛物线的一部分.
数据收集:
车棚与支柱的交点到地面的距离为,棚顶的最高点的竖直高度是,距离支柱的水平距离是,棚顶右端点距离支柱的水平距离是,车位的长为.已知棚顶的边缘与车位的边缘平齐.
问题解决:
以所在直线为轴,所在直线为轴建立平面直角坐标系.
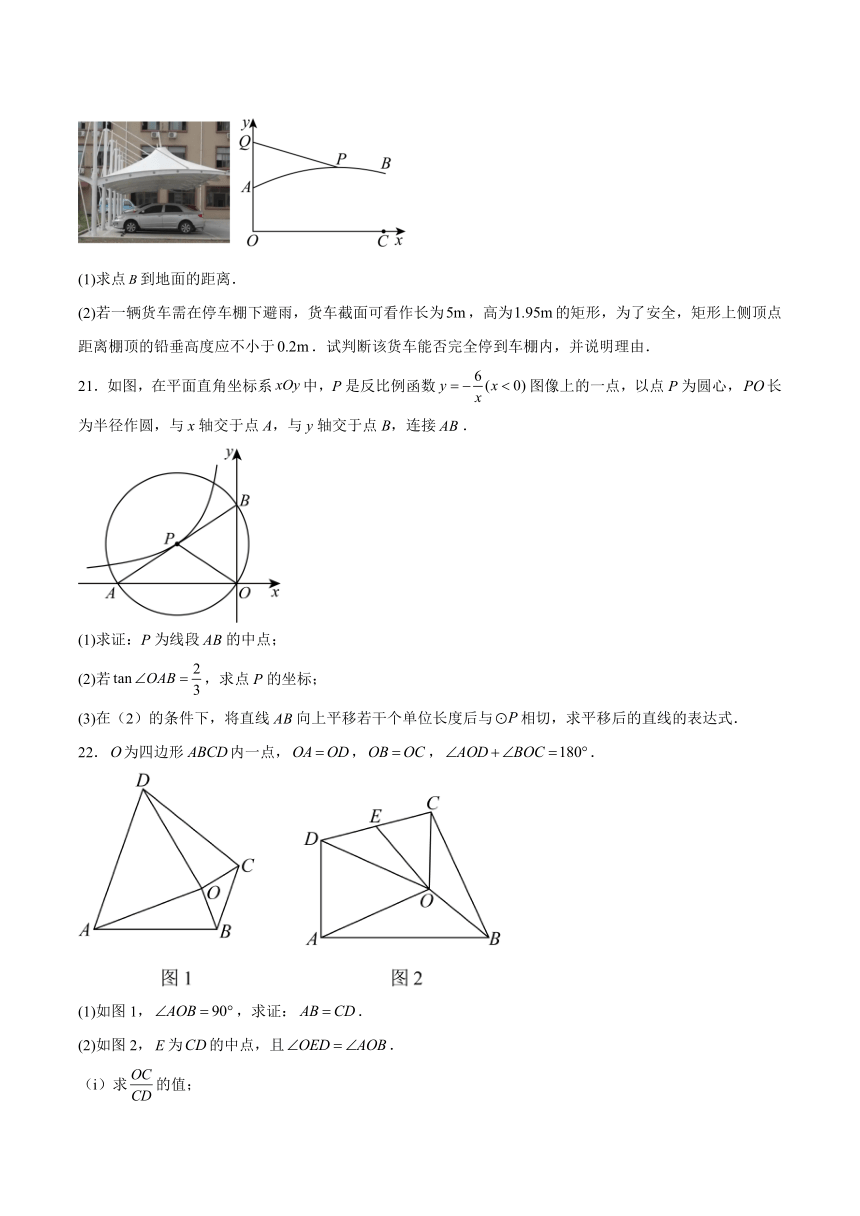
(1)求点到地面的距离.
(2)若一辆货车需在停车棚下避雨,货车截面可看作长为,高为的矩形,为了安全,矩形上侧顶点距离棚顶的铅垂高度应不小于.试判断该货车能否完全停到车棚内,并说明理由.
21.如图,在平面直角坐标系中,P是反比例函数图像上的一点,以点P为圆心,长为半径作圆,与x轴交于点A,与y轴交于点B,连接.
(1)求证:P为线段的中点;
(2)若,求点P的坐标;
(3)在(2)的条件下,将直线向上平移若干个单位长度后与相切,求平移后的直线的表达式.
22.为四边形内一点,,,.
(1)如图1,,求证:.
(2)如图2,为的中点,且.
(i)求的值;
(ii)求证:.
23.在平面直角坐标系中,点O为坐标的原点,抛物线交x轴于A、B两点,交y轴于点C,点A的坐标,点B的坐标.
(1)求、的值;
(2)如图1,点在线段上,过点作轴交抛物线于点、两点(点在点右侧),连接,设点的横坐标为,的面积为,求与的函数解析式(不要求写出自变量的取值范围);
(3)如图2,在(2)的条件下,点为抛物线的顶点,连接、,,点M为第一象限内点左侧抛物线上一点,连接、,点是线段的中点,连接.,点为第一象限内一点,连接、,,过点作于H,,过点作交x轴于点,求直线的解析式.
参考答案
1.B
解:A、1是有理数,不符合题意;
B、是无理数,符合题意;
C、是有理数,不符合题意;
D、2024是有理数,不符合题意;
故选:B.
2.C
解:,
故选:C.
3.B
解:由图可知,春晚主标识是中心对称图形不是轴对称图形,
故选:B.
4.C
解:A、,原式计算错误,不符合题意;
B、,原式计算错误,不符合题意;
C、,原式计算正确,符合题意;
D、,原式计算错误,不符合题意;
故选:C.
5.A
解:去分母,得
移项,得
合并同类项,得,
化系数为1,得,
解集在数轴上表示为:
故选:A.
6.D
【详解】∵∠AED与∠ABC都对,
∴∠AED=∠ABC,
在Rt△ABC中,AB=2,AC=1,
根据勾股定理得:BC= ,
则.
故答案为D.
7.C
解:A.对角线垂直且互相平分的四边形是菱形,所以A选项说法正确,故A选项不符合题意;
B.同圆或等圆中,同弧对应的圆周角相等,所以A选项说法正确,故B选项不符合题意;
C.对角线相等的四边形是不一定是矩形,所以C选项说法不正确,故C选项符合题意;
D.对角线垂直且相等的平行四边形是正方形,所以D选项说法正确,故D选项不符合题意.
故选:C.
8.A
解:∵,
∴图象经过第一、三象限,且在每一个象限内y随x的增大而减小,
∵,
∴点在第三象限,点在第一象限,
∴,
故选:A.
9.A
解:,
,
,
,
,
故选:A.
10.C
解:由轴对称的性质可得,
∴分别平分,
∴点E到和到的距离相等,
设点E到的距离为h,
∴,
∴,
同理可得,
∵,
∴,
∴,
∴,
∴,
∴,
∴,即,
∴,
∵,
∴,
∴,
∴,即,
∴,
∴,
故选:C.
11.
根据分式有意义的条件,分母不为0列出不等式求解.
【详解】在函数中,因为分式的分母不能为0,
所以,
解得,
即自变量的取值范围是.
故答案为:.
12.
解:原式,
故答案为:.
13.甲
解:∵甲、乙、丙三名同学进行跳远测试,每人10次跳远成绩的平均数都是,方差分别是,
∴甲的方差最大,
∴这三名同学跳远成绩最不稳定的是甲,
故答案为:甲.
14.11
解:,
,
,
故答案为:11.
15.①②③④
连接
∵矩形
∴
∵,
∴,故①正确;
∵G是的中点,
∴,故②正确;
∴,
∴
∵
∴
∴,故③正确;
作交于点H,则,
∴,
∵,
∴
∴,
∵,,
∴,
∴,,
∵G是的中点,
∴,
∴,
∴,
即
∵
∴
∴
∴,故④正确;
故答案为:①②③④.
16.
解:原式
.
17.(1)垂直平分线
(2)见解析
(1)解:由作图方法可得直线是的垂直平分线;
(2)证明:∵四边形是平行四边形,
∴,
∴,
∵是的垂直平分线,
∴,
∴,
∴,
∴,
∴.
18.(1);
(2)分
(3)
(1)解:人,
∴参与比赛的人数为40人,
∴,;
(2)解:分;
答:全部参赛选手成绩的平均分为分;
(3)解;画树状图如下:
由树状图可知任选两人共有12种等可能结果,其中是一名男生和一名女生的情况共有6种,
∴恰好是一名男生和一名女生的概率为
19.(1)第一批鲜桃的数量为;
(2)①;②前后一共获利元.
(1)解:设第一批鲜桃的进价为元,由第二批鲜桃的进价为元,
∴第一批鲜桃的数量为,第二批鲜桃的数量为,
根据题意得,解得,
经检验是原方程的解,且符合题意,
∴第一批鲜桃的数量为;
(2)解:①前两天每天销售,剩余,
∵第二批鲜桃的数量为,
∴总剩余数量为,
降价后,每天销售,两天共销售,
根据题意得,解得;
∵为整数,且保证销售量不超过总剩余量,
∴取;
②总成本为元,
总收入为
,
∴前后一共获利:元.
20.(1)点到地面的距离为
(2)该货车能完全停到车棚内,见解析
(1)解:棚顶的最高点的竖直高度是,距离支柱的水平距离是,
点的坐标为.
可设横截面所在抛物线的表达式为.
车棚与支柱的交点到地面的距离为,
点的坐标为.
把,得.
解得.
横截面所在抛物线的表达式为.
棚顶右端点距离支柱的水平距离是,
点的横坐标为6,
把,
得.
点到地面的距离为.
(2)解:该货车能完全停到车棚内.
理由:.
把,
得.
∴.
,
该货车能完全停到车棚内.
21.(1)见解析
(2)点的坐标为
(3)
(1)解:点A,O,B在上,且,
为的直径,
又;
为线段的中点.
(2)过点作,
设点的坐标为,则,.
∵,
∴
,
,
解得:(舍去)或,
点的坐标为.
(3)如图,过点作的垂线交于点(点在上方),过点作的平行线交轴于点,则,即为的切线.
由(2)可得:,,
,,,
∴,
设直线的表达式为,
将,代入,得,
解得
直线的表达式为,
如图,过点作于点,则,.
,
,
,
,
,
.
直线是由直线向上平移个单位长度得到的.
直线的函数表达式为.
22.(1)证明见解析
(2)(i),(ii)证明见解析
(1)证明:∵,,
∴,
∴,
又∵,,
∴,
∴.
(2)(i)解:∵,
∴,
又∵,
∴,即,
又∵,
∴,
又∵,
∴,
∴,即,,
∴.
(ii)证明:延长至点,使,
∵为的中点,
∴四边形是平行四边形,
∴,,
又∵,,,
∴,
又∵,,
∴,
∴,,
又∵,
∴,
∴,
又∵,,,,
∴,即,
∴.
23.(1)
(2)
(3)
(1)解:∵点A的坐标,点B的坐标
∴;
(2)解:∵点的横坐标为,,,
∴,,,
∴,
∴;
(3)解:如图,过点作于,过点作轴于,轴于,轴于,连接,
∵,点D为抛物线的顶点,
∴,,
设,
∵,
∴,
解得:,即,
∴,
∴,,
在和中,,
∴,
∴,
∵,
∴,
∴,,
∵,
∴,
∴,
∵,
∴,
∴,
∵,,
∴,
设,
∵,
∴,
∴,
解得:,
∴,
解得:,
∴,,,
∵,,
∴,
∵,
∴,
∴,
设,则,,
∴,
解得:,,
当时,,则,
∴不符合题意,舍去,
∴时,,,符合题意,
∴,,
∵,,
∴,
∴,
∴,,,
∴,
设,直线的解析式为,
∴,
解得:,
∵,
∴当时,,
解得:,
∴,,
∵点是线段ME的中点,
∴,
设直线的解析式为,
∴,
解得:,
∵,
∴,即,
解得:,
∴,
∵,
∴设直线解析式为,
∴,
解得:,
∴直线解析式为.
一、单选题
1.下列实数是无理数的是( )
A.1 B. C. D.2024
2.珠海长隆海洋王国的鲸鲨馆水体量约为立方米,将用科学记数法表示正确的是( )
A. B. C. D.
3.2025年春晚的主题是“巳巳如意,生生不息”,如图为春晚主标识,巧妙组合的两个“巳”字象征中国传统的如意纹样,寓意双巳合璧,带来事事如意的吉祥.下列关于该标识的说法正确的是( )
A.是轴对称图形不是中心对称图形
B.是中心对称图形不是轴对称图形
C.既是轴对称图形又是中心对称图形
D.既不是轴对称图形也不是中心对称图形
4.下列计算正确的是( )
A. B.
C. D.
5.不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
6.如图,边长为1的小正方形网格中,⊙O的圆心在格点上,则∠AED的余弦值是( )
A. B.1 C. D.
7.下列说法错误的是( )
A.对角线垂直且互相平分的四边形是菱形 B.同圆或等圆中,同弧对应的圆周角相等
C.对角线相等的四边形是矩形 D.对角线垂直且相等的平行四边形是正方形
8.已知点都在反比例函数的图象上,则的大小关系是( )
A. B.
C. D.
9.如图,是的内接三角形,,则的度数为( )
A. B. C. D.
10.如图,在中(),,点,分别是,上的动点,连接,,点和关于对称,点和关于对称,且点,都在所在的直线上.已知,设,.下列代数式的值不变的是( )
A. B. C. D.
二、填空题
11.在函数中,自变量x的取值范围是 .
12.计算: .
13.甲、乙、丙三名男同学进行跳远测试,每人10次跳远成绩的平均数都是,方差分别是,则这三名同学跳远成绩最不稳定的是 .
14.若,则 .
15.如图,在矩形中,,点E,F分别在边,上,交于点G,若G是的中点,下列四个结论中:①;②;③;④,正确的是 (填序号即可)
三、解答题
16.计算:
17.如图,在中,分别以为圆心,以大于的长为半径画弧,两弧交于点,作直线分别交于点,交于点.
(1)填空:直线是的___________;
(2)求证:.
18.黄梅戏是“中国五大戏曲剧种”之一,也是安徽省的主要地方戏曲剧种.为激发学生对黄梅戏的热爱,某校举行黄梅戏演唱比赛,将全部参赛选手的成绩(满分为100分,得分为正整数且无满分,最低为75分)分成五组:A:,B:,C:,D:,E:,并绘制了如下频数分布直方图和扇形统计图,部分信息如下:
请根据以上信息,完成下列问题:
(1)填空:频数分布直方图中,________,扇形统计图中,圆心角________;
(2)A,B,C,D,E这五组数据的平均数分别为77,82,87,92,97,计算全部参赛选手成绩的平均分;
(3)在E组的选手中有男生1名,女生3名,学校打算从这4名选手中随机选取2名参加市级比赛,求恰好选中一名男生和一名女生的概率.
19.鲜桃刚上市,某水果店率先用1000元购进了一批鲜桃,前两天以高于进价的价格卖出;第三天水果店又用1000元购进了一批鲜桃,由于进价降低了,这一批鲜桃多购进.
(1)求水果店购进第一批鲜桃的数量;
(2)注意到市场上鲜桃数量逐渐增多,水果店主决定将剩余和新进鲜桃在原销售价的基础上,全部降价元(为整数)销售.实际销售过程中,平均每天销售量相对于前两天平均每天增加了,仅仅销售两天,剩下量不超过.
①求的值;
②若店主将剩余鲜桃以20元的价格全部卖完,求前后一共获利多少元.
20.综合与实践
问题背景:
如图为一汽车停车棚及它的侧面示意图,其棚顶的横截面可以看作是抛物线的一部分.
数据收集:
车棚与支柱的交点到地面的距离为,棚顶的最高点的竖直高度是,距离支柱的水平距离是,棚顶右端点距离支柱的水平距离是,车位的长为.已知棚顶的边缘与车位的边缘平齐.
问题解决:
以所在直线为轴,所在直线为轴建立平面直角坐标系.
(1)求点到地面的距离.
(2)若一辆货车需在停车棚下避雨,货车截面可看作长为,高为的矩形,为了安全,矩形上侧顶点距离棚顶的铅垂高度应不小于.试判断该货车能否完全停到车棚内,并说明理由.
21.如图,在平面直角坐标系中,P是反比例函数图像上的一点,以点P为圆心,长为半径作圆,与x轴交于点A,与y轴交于点B,连接.
(1)求证:P为线段的中点;
(2)若,求点P的坐标;
(3)在(2)的条件下,将直线向上平移若干个单位长度后与相切,求平移后的直线的表达式.
22.为四边形内一点,,,.
(1)如图1,,求证:.
(2)如图2,为的中点,且.
(i)求的值;
(ii)求证:.
23.在平面直角坐标系中,点O为坐标的原点,抛物线交x轴于A、B两点,交y轴于点C,点A的坐标,点B的坐标.
(1)求、的值;
(2)如图1,点在线段上,过点作轴交抛物线于点、两点(点在点右侧),连接,设点的横坐标为,的面积为,求与的函数解析式(不要求写出自变量的取值范围);
(3)如图2,在(2)的条件下,点为抛物线的顶点,连接、,,点M为第一象限内点左侧抛物线上一点,连接、,点是线段的中点,连接.,点为第一象限内一点,连接、,,过点作于H,,过点作交x轴于点,求直线的解析式.
参考答案
1.B
解:A、1是有理数,不符合题意;
B、是无理数,符合题意;
C、是有理数,不符合题意;
D、2024是有理数,不符合题意;
故选:B.
2.C
解:,
故选:C.
3.B
解:由图可知,春晚主标识是中心对称图形不是轴对称图形,
故选:B.
4.C
解:A、,原式计算错误,不符合题意;
B、,原式计算错误,不符合题意;
C、,原式计算正确,符合题意;
D、,原式计算错误,不符合题意;
故选:C.
5.A
解:去分母,得
移项,得
合并同类项,得,
化系数为1,得,
解集在数轴上表示为:
故选:A.
6.D
【详解】∵∠AED与∠ABC都对,
∴∠AED=∠ABC,
在Rt△ABC中,AB=2,AC=1,
根据勾股定理得:BC= ,
则.
故答案为D.
7.C
解:A.对角线垂直且互相平分的四边形是菱形,所以A选项说法正确,故A选项不符合题意;
B.同圆或等圆中,同弧对应的圆周角相等,所以A选项说法正确,故B选项不符合题意;
C.对角线相等的四边形是不一定是矩形,所以C选项说法不正确,故C选项符合题意;
D.对角线垂直且相等的平行四边形是正方形,所以D选项说法正确,故D选项不符合题意.
故选:C.
8.A
解:∵,
∴图象经过第一、三象限,且在每一个象限内y随x的增大而减小,
∵,
∴点在第三象限,点在第一象限,
∴,
故选:A.
9.A
解:,
,
,
,
,
故选:A.
10.C
解:由轴对称的性质可得,
∴分别平分,
∴点E到和到的距离相等,
设点E到的距离为h,
∴,
∴,
同理可得,
∵,
∴,
∴,
∴,
∴,
∴,
∴,即,
∴,
∵,
∴,
∴,
∴,即,
∴,
∴,
故选:C.
11.
根据分式有意义的条件,分母不为0列出不等式求解.
【详解】在函数中,因为分式的分母不能为0,
所以,
解得,
即自变量的取值范围是.
故答案为:.
12.
解:原式,
故答案为:.
13.甲
解:∵甲、乙、丙三名同学进行跳远测试,每人10次跳远成绩的平均数都是,方差分别是,
∴甲的方差最大,
∴这三名同学跳远成绩最不稳定的是甲,
故答案为:甲.
14.11
解:,
,
,
故答案为:11.
15.①②③④
连接
∵矩形
∴
∵,
∴,故①正确;
∵G是的中点,
∴,故②正确;
∴,
∴
∵
∴
∴,故③正确;
作交于点H,则,
∴,
∵,
∴
∴,
∵,,
∴,
∴,,
∵G是的中点,
∴,
∴,
∴,
即
∵
∴
∴
∴,故④正确;
故答案为:①②③④.
16.
解:原式
.
17.(1)垂直平分线
(2)见解析
(1)解:由作图方法可得直线是的垂直平分线;
(2)证明:∵四边形是平行四边形,
∴,
∴,
∵是的垂直平分线,
∴,
∴,
∴,
∴,
∴.
18.(1);
(2)分
(3)
(1)解:人,
∴参与比赛的人数为40人,
∴,;
(2)解:分;
答:全部参赛选手成绩的平均分为分;
(3)解;画树状图如下:
由树状图可知任选两人共有12种等可能结果,其中是一名男生和一名女生的情况共有6种,
∴恰好是一名男生和一名女生的概率为
19.(1)第一批鲜桃的数量为;
(2)①;②前后一共获利元.
(1)解:设第一批鲜桃的进价为元,由第二批鲜桃的进价为元,
∴第一批鲜桃的数量为,第二批鲜桃的数量为,
根据题意得,解得,
经检验是原方程的解,且符合题意,
∴第一批鲜桃的数量为;
(2)解:①前两天每天销售,剩余,
∵第二批鲜桃的数量为,
∴总剩余数量为,
降价后,每天销售,两天共销售,
根据题意得,解得;
∵为整数,且保证销售量不超过总剩余量,
∴取;
②总成本为元,
总收入为
,
∴前后一共获利:元.
20.(1)点到地面的距离为
(2)该货车能完全停到车棚内,见解析
(1)解:棚顶的最高点的竖直高度是,距离支柱的水平距离是,
点的坐标为.
可设横截面所在抛物线的表达式为.
车棚与支柱的交点到地面的距离为,
点的坐标为.
把,得.
解得.
横截面所在抛物线的表达式为.
棚顶右端点距离支柱的水平距离是,
点的横坐标为6,
把,
得.
点到地面的距离为.
(2)解:该货车能完全停到车棚内.
理由:.
把,
得.
∴.
,
该货车能完全停到车棚内.
21.(1)见解析
(2)点的坐标为
(3)
(1)解:点A,O,B在上,且,
为的直径,
又;
为线段的中点.
(2)过点作,
设点的坐标为,则,.
∵,
∴
,
,
解得:(舍去)或,
点的坐标为.
(3)如图,过点作的垂线交于点(点在上方),过点作的平行线交轴于点,则,即为的切线.
由(2)可得:,,
,,,
∴,
设直线的表达式为,
将,代入,得,
解得
直线的表达式为,
如图,过点作于点,则,.
,
,
,
,
,
.
直线是由直线向上平移个单位长度得到的.
直线的函数表达式为.
22.(1)证明见解析
(2)(i),(ii)证明见解析
(1)证明:∵,,
∴,
∴,
又∵,,
∴,
∴.
(2)(i)解:∵,
∴,
又∵,
∴,即,
又∵,
∴,
又∵,
∴,
∴,即,,
∴.
(ii)证明:延长至点,使,
∵为的中点,
∴四边形是平行四边形,
∴,,
又∵,,,
∴,
又∵,,
∴,
∴,,
又∵,
∴,
∴,
又∵,,,,
∴,即,
∴.
23.(1)
(2)
(3)
(1)解:∵点A的坐标,点B的坐标
∴;
(2)解:∵点的横坐标为,,,
∴,,,
∴,
∴;
(3)解:如图,过点作于,过点作轴于,轴于,轴于,连接,
∵,点D为抛物线的顶点,
∴,,
设,
∵,
∴,
解得:,即,
∴,
∴,,
在和中,,
∴,
∴,
∵,
∴,
∴,,
∵,
∴,
∴,
∵,
∴,
∴,
∵,,
∴,
设,
∵,
∴,
∴,
解得:,
∴,
解得:,
∴,,,
∵,,
∴,
∵,
∴,
∴,
设,则,,
∴,
解得:,,
当时,,则,
∴不符合题意,舍去,
∴时,,,符合题意,
∴,,
∵,,
∴,
∴,
∴,,,
∴,
设,直线的解析式为,
∴,
解得:,
∵,
∴当时,,
解得:,
∴,,
∵点是线段ME的中点,
∴,
设直线的解析式为,
∴,
解得:,
∵,
∴,即,
解得:,
∴,
∵,
∴设直线解析式为,
∴,
解得:,
∴直线解析式为.
同课章节目录
