2024-2025学年江苏省连云港市海州区凤凰学校九年级(下)第一次段考数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年江苏省连云港市海州区凤凰学校九年级(下)第一次段考数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 144.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-16 21:22:54 | ||
图片预览




文档简介
2024-2025学年江苏省连云港市海州区凤凰学校九年级(下)第一次段考数学试卷
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.实数-2的相反数是( )
A. -2 B. 2 C. D.
2.2023年5月1日,南京夫子庙、中山陵、玄武湖、雨花台四大景区共接待游客约6060000人,这个数可用科学记数法表示为( )
A. 0.606×105 B. 6.06×105 C. 6.0×106 D. 6.06×106
3.下列运算中,正确的是( )
A. 2x 3x2=5x3 B. x4+x2=x6 C. (x2y)3=x6y3 D. (x+1)2=x2+1
4.在Rt△ABC中,∠C=90°,BC=5,AC=12,则sinB的值是( )
A. B. C. D.
5.若正多边形的一个外角等于45°,则这个正多边形的边数是( )
A. 六 B. 七 C. 八 D. 九
6.2,,5三个数的大小关系是( )
A. 5<<2 B. <5<2 C. 2<5< D. <2<5
7.如图,正五边形ABCDE内接于⊙O,点F在弧AE上.若∠CDF=95°,则∠FCD的大小为( )
A. 38° B. 42° C. 49° D. 58°
8.如图,直线y=x+1、y=x-1与双曲线分别相交于点A、B、C、D.若四边形ABCD的面积为4,则k的值是( )
A.
B.
C.
D. 1
二、填空题:本题共8小题,每小题3分,共24分。
9.若代数式有意义,则实数x的取值范围是______.
10.分解因式:2a2-18=______.
11.若扇形的圆心角为45°,半径为3,则该扇形的弧长为______.
12.已知关于x的方程x2+2x-a=0的一个根为2,则另一个根是______.
13.已知关于x的一元二次方程x2-2x-3m2=0的两根分别为α、β,则α+β=______.
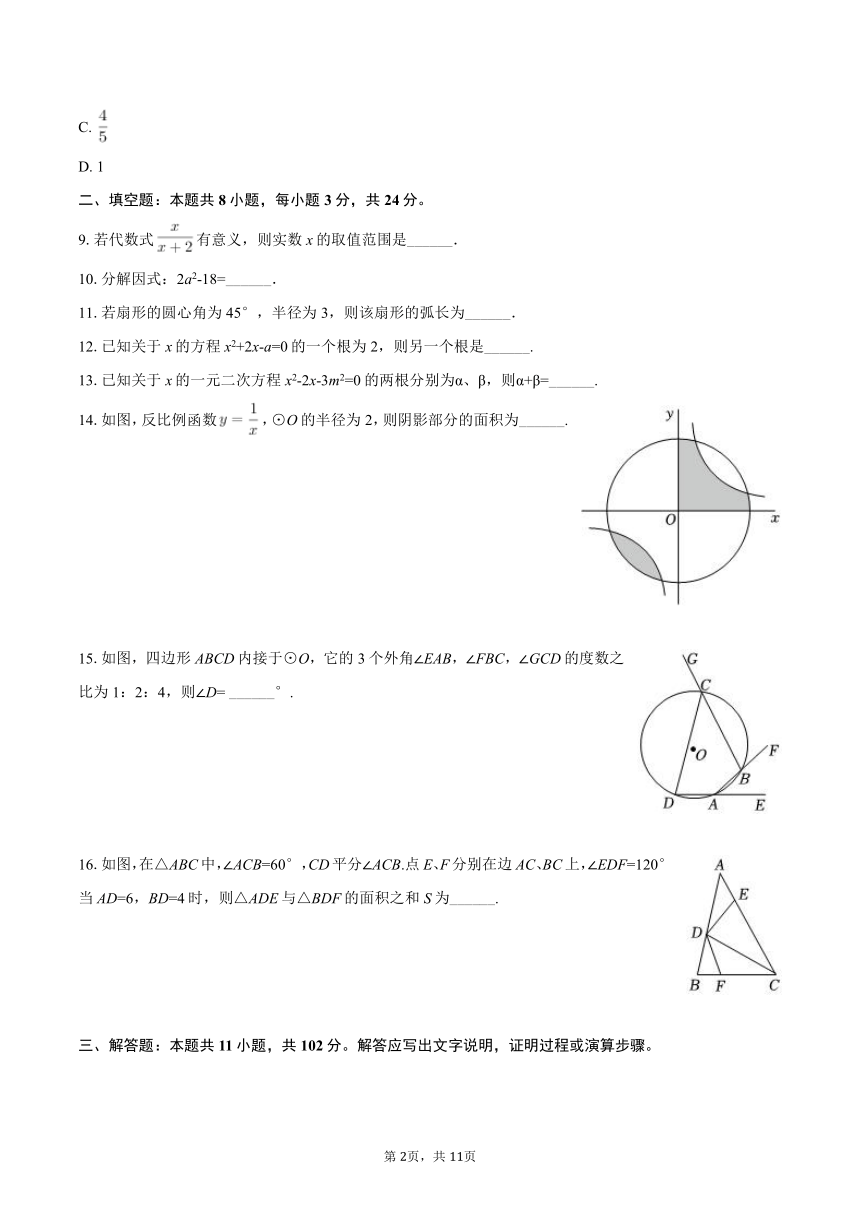
14.如图,反比例函数,⊙O的半径为2,则阴影部分的面积为______.
15.如图,四边形ABCD内接于⊙O,它的3个外角∠EAB,∠FBC,∠GCD的度数之比为1:2:4,则∠D= ______°.
16.如图,在△ABC中,∠ACB=60°,CD平分∠ACB.点E、F分别在边AC、BC上,∠EDF=120°,当AD=6,BD=4时,则△ADE与△BDF的面积之和S为______.
三、解答题:本题共11小题,共102分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题6分)
计算:.
18.(本小题6分)
解不等式组:.
19.(本小题6分)
化简:.
20.(本小题8分)
有甲乙两个不透明的布袋,甲袋中有两个完全相同的小球,分别标有数字-1、,乙袋中有三个完全相同的小球,分别标有数字0、-1、-2,小丽先从甲袋中随机取出一个小球,记录下小球上的数字为x;再从乙袋中随机取出一个小球,记录下小球上的数字为y,设点P坐标为(x,y).
(1)请用表格或树状图列出点P所有可能的坐标;
(2)在平面直角坐标系xOy中,求点P在第四象限的概率.
21.(本小题8分)
为了解某校九年级学生周末活动情况,随机抽取了部分学生进行调查,并绘制了如图所示的两幅不完整的统计表和统计图.
学生参加周末活动人数统计表
活动名称 人数
A.课外阅读 40
B.社会实践 48
C.家务劳动 m
D.户外运动 n
E.其它活动 26
请结合图表中提供的信息,解答下列问题:
(1)m= ______,n= ______;
(2)扇形统计图中A对应的圆心角是______度;
(3)若该校九年级有800名学生,请估算该校九年级周末参加家务劳动的人数.
22.(本小题10分)
如图,B、E、C、F是直线l上的四点,AB=DE,AC=DF,BE=CF.
(1)求证:△ABC≌△DEF;
(2)点P、Q分别是△ABC、△DEF的内心.
①用直尺和圆规作出点Q(保留作图痕迹,不要求写作法);
②连接PQ,则PQ与BE的关系是______.
23.(本小题10分)
某商场销售甲、乙两种商品,其中甲商品进价40元/件,售价50元/件;乙商品进价50元/件,售价80元/件.现商场用12500元购入这两种商品并全部售出,获得总利润4000元,则该商场购进甲、乙两种商品各多少件?
24.(本小题10分)
如图,在平面直角坐标系中,直线与x轴、y轴分别交于A、B两点,与双曲线y=在第一象限的一支交于点C,且AB=3BC.
(1)求k的值;
(2)设点D是x轴上的一个动点,线段CD与双曲线交于另一点E,连接AE,当AE平分△ACD的面积时,直接写出点D的坐标是______.
25.(本小题12分)
如图为某影院的剖面图,水平地面AE=9m,斜坡AC的坡度i=1:2.4,小丽从A处沿斜坡走了13m到B处,入座后,眼睛D观察屏幕最高处仰角为30°,屏幕最低处俯角为10°.
(1)小丽从A处走到B处,沿垂直方向上升了几米?
(2)求屏幕MN的高度?(sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,,结果精确到0.1m)
26.(本小题12分)
如图,二次函数y=x2+bx-4的图象与x轴相交于点A(-2,0),B,其顶点是C.
(1)b= ______;
(2)D是第三象限抛物线上的一点,连接OD,tan∠AOD=.将原抛物线向左平移,使得平移后的抛物线经过点D,过点(k,0)作x轴的垂线l.已知在l的左侧,平移前后的两条抛物线都下降,求k的取值范围;
(3)将原抛物线平移,平移后的抛物线与原抛物线的对称轴相交于点Q,且其顶点P落在原抛物线上,连接PC、QC、PQ.已知△PCQ是直角三角形,求点P的坐标.
27.(本小题14分)
如图1,四边形ABCD中,AD∥BC,∠B=90°,,CD=10.
(1)线段AB= ______;
(2)如图2,点O是CD的中点,E、F分别是AD、BC上的点,将△DEO沿着EO翻折得△GEO,将△COF沿着FO翻折使CO与GO重合,设DE=x,CF=y.
①求y与x之间的函数关系;
②当点E从点D运动到点A时,点G走过的路径长为,求AD的长;
③△EOF面积的最小值为______.
1.【答案】B
2.【答案】D
3.【答案】C
4.【答案】D
5.【答案】C
6.【答案】C
7.【答案】C
8.【答案】A
9.【答案】x≠-2
10.【答案】2(a+3)(a-3)
11.【答案】π
12.【答案】-4
13.【答案】2
14.【答案】π
15.【答案】72
16.【答案】
17.【答案】解:
=
=.
18.【答案】-4<x≤3.
19.【答案】.
20.【答案】(1)用树状图表示所有等可能出现的结果如下:
∴点P的坐标可能为:(-1,0),(-1,-1),(-1,-2),(,0),(,-1),(,-2);
(2)共有6种等可能出现的结果,其中点P在第四象限的有2种,
∴点P在第四象限的概率为=.
21.【答案】解:(1)24;62;
(2)72;
(3)800=96(人),
答:该校九年级周末参加家务劳动的人数约有96人.
22.【答案】(1)证明:∵BE=CF,
∴BE+EC=CF+EC,
∴BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS);
(2)解:①如图,点Q即为所求;
②PQ∥BE,PQ=BE
23.【答案】解:设该商场购进甲种商品x件,乙种商品y件,
由题意得:,
解得:,
答:该商场购进甲种商品250件,乙种商品50件.
24.【答案】(1)∵直线与x轴、y轴分别交于A、B两点,
∴A(-4,0),B(0,3),
∴OA=4,OB=3.
∵AB=3BC,
∴=.
如图,过C点作CF⊥x轴于点F,则OB∥CF,
∴△AOB∽△AFC,
∴===,
∴===,
∴AF=,FC=4,
∴OF=AF-OA=-4=,
∴C(,4),
∵双曲线y=过点C,
∴k=×4=;
(2)(4,0).
25.【答案】解:(1)延长DB交EA于点F,
由题意得:DF⊥EF,
∵斜坡AC的坡度i=1:2.4,
∴==,
∴设BF=5x米,则AF=12x米,
在Rt△ABF中,AB===13x(米),
∵AB=13米,
∴13x=13,
解得:x=1,
∴AF=12米,BF=5米,
∴小丽从A处走到B处,沿垂直方向上升了5米;
(2)过点D作DG⊥MN,垂足为G,
由题意得:DG=EF,
∵AE=9米,AF=12米,
∴DG=EF=AE+AF=21(米),
在Rt△MDG中,∠MDG=30°,
∴MG=DG tan30°=21×=7(米),
在Rt△NDG中,∠NDG=10°,
∴GN=DG tan10°≈21×0.18=3.78(米),
∴MN=MG+GN=7+3.78≈15.9(米),
∴屏幕MN的高度约为15.9米.
26.【答案】解:(1)-1;
(2)∵tan∠AOD=,
∴设D(2t,5t),
∴,
∴t1=-,t2=4(舍去),
∴D(-1,-),
∵y=-x-4=(x-1)2-,
∴新抛物线设为:y=(x-m)2-,
∴-,
∴m1=-3,m2=1(舍去),
∴y=(x+3)2-,
∵在l的左侧,平移前后的两条抛物线都下降,
∴k≤-3;
(3)如图,
作PV⊥CQ 于V,
设P(t,),
∴平移后的抛物线为:y=(x-t)2+(),
当x=1时,y=t2-2t-,
∴Q(1,t2-2t-),
∵>0,
∴∠CPQ=90°,
∵QV=(t2-2t-)-()=-t,
CV=(-t-4)-(-)=-t+,
∴QV=CV,
∴PV=CV=QV,
∴|t-1|=,
∴t1=3,t2=-1,t3=t4=1(舍去),
当t=3时,y=32-3-4=-,
当t=-1时,y=(-1)2-(-1)-4=-,
∴P(3,-)或(-1,-).
27.【答案】8 16
第1页,共1页
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.实数-2的相反数是( )
A. -2 B. 2 C. D.
2.2023年5月1日,南京夫子庙、中山陵、玄武湖、雨花台四大景区共接待游客约6060000人,这个数可用科学记数法表示为( )
A. 0.606×105 B. 6.06×105 C. 6.0×106 D. 6.06×106
3.下列运算中,正确的是( )
A. 2x 3x2=5x3 B. x4+x2=x6 C. (x2y)3=x6y3 D. (x+1)2=x2+1
4.在Rt△ABC中,∠C=90°,BC=5,AC=12,则sinB的值是( )
A. B. C. D.
5.若正多边形的一个外角等于45°,则这个正多边形的边数是( )
A. 六 B. 七 C. 八 D. 九
6.2,,5三个数的大小关系是( )
A. 5<<2 B. <5<2 C. 2<5< D. <2<5
7.如图,正五边形ABCDE内接于⊙O,点F在弧AE上.若∠CDF=95°,则∠FCD的大小为( )
A. 38° B. 42° C. 49° D. 58°
8.如图,直线y=x+1、y=x-1与双曲线分别相交于点A、B、C、D.若四边形ABCD的面积为4,则k的值是( )
A.
B.
C.
D. 1
二、填空题:本题共8小题,每小题3分,共24分。
9.若代数式有意义,则实数x的取值范围是______.
10.分解因式:2a2-18=______.
11.若扇形的圆心角为45°,半径为3,则该扇形的弧长为______.
12.已知关于x的方程x2+2x-a=0的一个根为2,则另一个根是______.
13.已知关于x的一元二次方程x2-2x-3m2=0的两根分别为α、β,则α+β=______.
14.如图,反比例函数,⊙O的半径为2,则阴影部分的面积为______.
15.如图,四边形ABCD内接于⊙O,它的3个外角∠EAB,∠FBC,∠GCD的度数之比为1:2:4,则∠D= ______°.
16.如图,在△ABC中,∠ACB=60°,CD平分∠ACB.点E、F分别在边AC、BC上,∠EDF=120°,当AD=6,BD=4时,则△ADE与△BDF的面积之和S为______.
三、解答题:本题共11小题,共102分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题6分)
计算:.
18.(本小题6分)
解不等式组:.
19.(本小题6分)
化简:.
20.(本小题8分)
有甲乙两个不透明的布袋,甲袋中有两个完全相同的小球,分别标有数字-1、,乙袋中有三个完全相同的小球,分别标有数字0、-1、-2,小丽先从甲袋中随机取出一个小球,记录下小球上的数字为x;再从乙袋中随机取出一个小球,记录下小球上的数字为y,设点P坐标为(x,y).
(1)请用表格或树状图列出点P所有可能的坐标;
(2)在平面直角坐标系xOy中,求点P在第四象限的概率.
21.(本小题8分)
为了解某校九年级学生周末活动情况,随机抽取了部分学生进行调查,并绘制了如图所示的两幅不完整的统计表和统计图.
学生参加周末活动人数统计表
活动名称 人数
A.课外阅读 40
B.社会实践 48
C.家务劳动 m
D.户外运动 n
E.其它活动 26
请结合图表中提供的信息,解答下列问题:
(1)m= ______,n= ______;
(2)扇形统计图中A对应的圆心角是______度;
(3)若该校九年级有800名学生,请估算该校九年级周末参加家务劳动的人数.
22.(本小题10分)
如图,B、E、C、F是直线l上的四点,AB=DE,AC=DF,BE=CF.
(1)求证:△ABC≌△DEF;
(2)点P、Q分别是△ABC、△DEF的内心.
①用直尺和圆规作出点Q(保留作图痕迹,不要求写作法);
②连接PQ,则PQ与BE的关系是______.
23.(本小题10分)
某商场销售甲、乙两种商品,其中甲商品进价40元/件,售价50元/件;乙商品进价50元/件,售价80元/件.现商场用12500元购入这两种商品并全部售出,获得总利润4000元,则该商场购进甲、乙两种商品各多少件?
24.(本小题10分)
如图,在平面直角坐标系中,直线与x轴、y轴分别交于A、B两点,与双曲线y=在第一象限的一支交于点C,且AB=3BC.
(1)求k的值;
(2)设点D是x轴上的一个动点,线段CD与双曲线交于另一点E,连接AE,当AE平分△ACD的面积时,直接写出点D的坐标是______.
25.(本小题12分)
如图为某影院的剖面图,水平地面AE=9m,斜坡AC的坡度i=1:2.4,小丽从A处沿斜坡走了13m到B处,入座后,眼睛D观察屏幕最高处仰角为30°,屏幕最低处俯角为10°.
(1)小丽从A处走到B处,沿垂直方向上升了几米?
(2)求屏幕MN的高度?(sin10°≈0.17,cos10°≈0.98,tan10°≈0.18,,结果精确到0.1m)
26.(本小题12分)
如图,二次函数y=x2+bx-4的图象与x轴相交于点A(-2,0),B,其顶点是C.
(1)b= ______;
(2)D是第三象限抛物线上的一点,连接OD,tan∠AOD=.将原抛物线向左平移,使得平移后的抛物线经过点D,过点(k,0)作x轴的垂线l.已知在l的左侧,平移前后的两条抛物线都下降,求k的取值范围;
(3)将原抛物线平移,平移后的抛物线与原抛物线的对称轴相交于点Q,且其顶点P落在原抛物线上,连接PC、QC、PQ.已知△PCQ是直角三角形,求点P的坐标.
27.(本小题14分)
如图1,四边形ABCD中,AD∥BC,∠B=90°,,CD=10.
(1)线段AB= ______;
(2)如图2,点O是CD的中点,E、F分别是AD、BC上的点,将△DEO沿着EO翻折得△GEO,将△COF沿着FO翻折使CO与GO重合,设DE=x,CF=y.
①求y与x之间的函数关系;
②当点E从点D运动到点A时,点G走过的路径长为,求AD的长;
③△EOF面积的最小值为______.
1.【答案】B
2.【答案】D
3.【答案】C
4.【答案】D
5.【答案】C
6.【答案】C
7.【答案】C
8.【答案】A
9.【答案】x≠-2
10.【答案】2(a+3)(a-3)
11.【答案】π
12.【答案】-4
13.【答案】2
14.【答案】π
15.【答案】72
16.【答案】
17.【答案】解:
=
=.
18.【答案】-4<x≤3.
19.【答案】.
20.【答案】(1)用树状图表示所有等可能出现的结果如下:
∴点P的坐标可能为:(-1,0),(-1,-1),(-1,-2),(,0),(,-1),(,-2);
(2)共有6种等可能出现的结果,其中点P在第四象限的有2种,
∴点P在第四象限的概率为=.
21.【答案】解:(1)24;62;
(2)72;
(3)800=96(人),
答:该校九年级周末参加家务劳动的人数约有96人.
22.【答案】(1)证明:∵BE=CF,
∴BE+EC=CF+EC,
∴BC=EF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SSS);
(2)解:①如图,点Q即为所求;
②PQ∥BE,PQ=BE
23.【答案】解:设该商场购进甲种商品x件,乙种商品y件,
由题意得:,
解得:,
答:该商场购进甲种商品250件,乙种商品50件.
24.【答案】(1)∵直线与x轴、y轴分别交于A、B两点,
∴A(-4,0),B(0,3),
∴OA=4,OB=3.
∵AB=3BC,
∴=.
如图,过C点作CF⊥x轴于点F,则OB∥CF,
∴△AOB∽△AFC,
∴===,
∴===,
∴AF=,FC=4,
∴OF=AF-OA=-4=,
∴C(,4),
∵双曲线y=过点C,
∴k=×4=;
(2)(4,0).
25.【答案】解:(1)延长DB交EA于点F,
由题意得:DF⊥EF,
∵斜坡AC的坡度i=1:2.4,
∴==,
∴设BF=5x米,则AF=12x米,
在Rt△ABF中,AB===13x(米),
∵AB=13米,
∴13x=13,
解得:x=1,
∴AF=12米,BF=5米,
∴小丽从A处走到B处,沿垂直方向上升了5米;
(2)过点D作DG⊥MN,垂足为G,
由题意得:DG=EF,
∵AE=9米,AF=12米,
∴DG=EF=AE+AF=21(米),
在Rt△MDG中,∠MDG=30°,
∴MG=DG tan30°=21×=7(米),
在Rt△NDG中,∠NDG=10°,
∴GN=DG tan10°≈21×0.18=3.78(米),
∴MN=MG+GN=7+3.78≈15.9(米),
∴屏幕MN的高度约为15.9米.
26.【答案】解:(1)-1;
(2)∵tan∠AOD=,
∴设D(2t,5t),
∴,
∴t1=-,t2=4(舍去),
∴D(-1,-),
∵y=-x-4=(x-1)2-,
∴新抛物线设为:y=(x-m)2-,
∴-,
∴m1=-3,m2=1(舍去),
∴y=(x+3)2-,
∵在l的左侧,平移前后的两条抛物线都下降,
∴k≤-3;
(3)如图,
作PV⊥CQ 于V,
设P(t,),
∴平移后的抛物线为:y=(x-t)2+(),
当x=1时,y=t2-2t-,
∴Q(1,t2-2t-),
∵>0,
∴∠CPQ=90°,
∵QV=(t2-2t-)-()=-t,
CV=(-t-4)-(-)=-t+,
∴QV=CV,
∴PV=CV=QV,
∴|t-1|=,
∴t1=3,t2=-1,t3=t4=1(舍去),
当t=3时,y=32-3-4=-,
当t=-1时,y=(-1)2-(-1)-4=-,
∴P(3,-)或(-1,-).
27.【答案】8 16
第1页,共1页
同课章节目录
