2024-2025学年上海市华东师大二附中七年级(下)随堂作业数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年上海市华东师大二附中七年级(下)随堂作业数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 84.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 10:21:32 | ||
图片预览

文档简介
2024-2025学年上海市华东师大二附中七年级(下)随堂作业数学试卷
一、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列命题中,是真命题的是( )
A. 两条直线被第三条直线所截,同位角相等
B. 过一点有无数条直线与已知直线平行
C. 在同一平面内,垂直于同一条直线的两条直线平行
D. 直线外一点到这条直线的垂线段叫做这点到直线的距离
2.在生物实验课上,老师布置了“测量锥形瓶内部底面内径”的任务.小亮同学想到了以下这个方案:如图,用螺丝钉将两根小棒AD,BC的中点O固定,利用全等三角形的性质,只要测得C,D之间的距离,就可知道内径AB的长度.此方案中,判定△AOB和△DOC是全等三角形的依据是( )
A. SSS B. SAS C. ASA D. AAS
3.如图①是某种型号拉杆箱的实物图,如图②是它的示意图,行李箱的侧面可看成一个矩形,点F,C,D在同一条直线上,为了拉箱时的舒适度,现将∠ABD调整为75°,若∠D保持不变,则图中∠ECF应( )
A. 减少20° B. 减少10° C. 增加20° D. 增加10°
4.若关于x的不等式ax-b>0的解集为x<,则关于x的不等式(a+b)x>b-a的解集是( )
A. B. C. D.
二、填空题:本题共8小题,每小题5分,共40分。
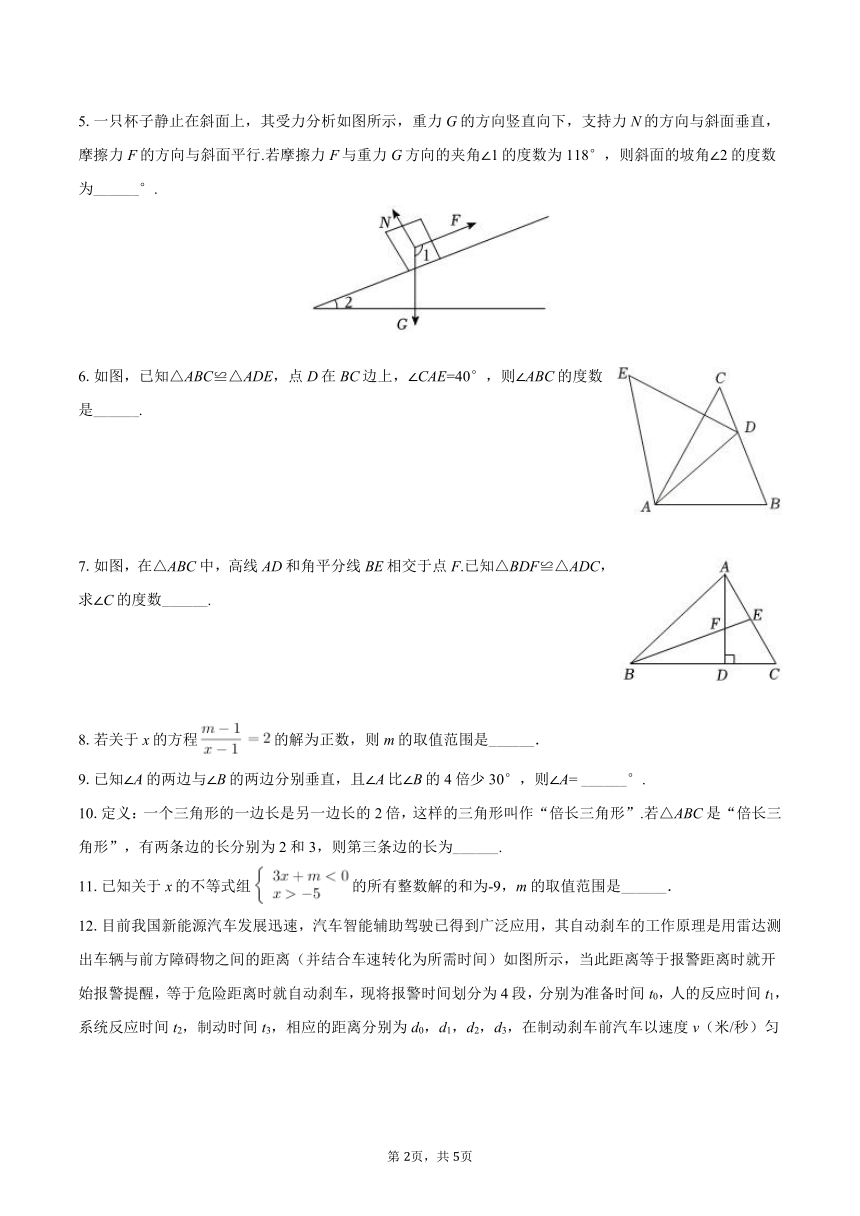
5.一只杯子静止在斜面上,其受力分析如图所示,重力G的方向竖直向下,支持力N的方向与斜面垂直,摩擦力F的方向与斜面平行.若摩擦力F与重力G方向的夹角∠1的度数为118°,则斜面的坡角∠2的度数为______°.
6.如图,已知△ABC≌△ADE,点D在BC边上,∠CAE=40°,则∠ABC的度数是______.
7.如图,在△ABC中,高线AD和角平分线BE相交于点F.已知△BDF≌△ADC,求∠C的度数______.
8.若关于x的方程的解为正数,则m的取值范围是______.
9.已知∠A的两边与∠B的两边分别垂直,且∠A比∠B的4倍少30°,则∠A= ______°.
10.定义:一个三角形的一边长是另一边长的2倍,这样的三角形叫作“倍长三角形”.若△ABC是“倍长三角形”,有两条边的长分别为2和3,则第三条边的长为______.
11.已知关于x的不等式组的所有整数解的和为-9,m的取值范围是______.
12.目前我国新能源汽车发展迅速,汽车智能辅助驾驶已得到广泛应用,其自动刹车的工作原理是用雷达测出车辆与前方障碍物之间的距离(并结合车速转化为所需时间)如图所示,当此距离等于报警距离时就开始报警提醒,等于危险距离时就自动刹车,现将报警时间划分为4段,分别为准备时间t0,人的反应时间t1,系统反应时间t2,制动时间t3,相应的距离分别为d0,d1,d2,d3,在制动刹车前汽车以速度v(米/秒)匀速运动,通过大数据统计分析得到如表一信息(其中系数k随地面湿滑程度等路面情况而变化,1≤k≤2)
阶段 0.准备 1.人的反应 2.系统反应 3.制动
时间 t0 t1=0.8秒 t2=0.2砂 t3
距离 d0=10米 d1 d2 d3=米
若要求汽车不论在何种路面情况下行驶,报警距离均小于60米,则汽车的行驶速度v应限制在______米/秒以下.
三、解答题:本题共4小题,共40分。解答应写出文字说明,证明过程或演算步骤。
13.(本小题10分)
(1)解下列不等式;
(2)解不等式组,并写出它的整数解.
14.(本小题10分)
为了丰富同学们的业余生活和培养同学们学习数学的兴趣,学校每年会举行一系列的数学文化节活动,为此学校计划购买A、B两种文化节的奖品作为纪念品.已知购买1件A种奖品与2件B种奖品共需要70元,购买2件A种奖品与3件B种奖品共需要120元.
(1)求A种奖品和B种奖品的单价分别为多少元?
(2)学校计划购买A种奖品和B种奖品共200件,总费用不超过5000元,那么最多能购买A种奖品多少件?
15.(本小题10分)
“抖空竹”是国家级非物质文化遗产.“抖空竹”的一个瞬间如图1所示,将图1抽象成一个数学问题:
(1)如图2,若AB∥|CD,∠EAB=75°,∠ECD=110°,求∠E的度数.
(2)已知AB∥CD,点E为AB,CD之外任意一点.
①如图3,探究∠BED与∠B,∠D之间的数量关系,请直接写出结果;
②如图4,探究∠CDE与∠B,∠BED之间的数量关系,请直接写出结果.
16.(本小题10分)
如图1,等边△ABC与等边△ECD的顶点B,C,D三点在一条直线上,连接AD,BE,两线相交于点F.
(1)求∠BFD的度数;
(2)如图2,连接FC,
①求证:FB是∠AFC的平分线;
②若AF=4,CF=2,求BF的长度.
1.【答案】C
2.【答案】B
3.【答案】C
4.【答案】A
5.【答案】28
6.【答案】70°
7.【答案】67.5°
8.【答案】m>-1且m≠1
9.【答案】10或138
10.【答案】1.5或4
11.【答案】3≤m<6或-6≤m<-3
12.【答案】25
13.【答案】x;
-4≤x<,整数解为-4,-3,-2,-1,0.
14.【答案】A种奖品的单价是30元,B种奖品的单价是20元;
最多能购买A种奖品100件.
15.【答案】35°;
①∠BED=∠D-∠B;②∠B=∠BED+∠CDE.
16.【答案】120°;
①见解析;
②6.
第1页,共1页
一、选择题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列命题中,是真命题的是( )
A. 两条直线被第三条直线所截,同位角相等
B. 过一点有无数条直线与已知直线平行
C. 在同一平面内,垂直于同一条直线的两条直线平行
D. 直线外一点到这条直线的垂线段叫做这点到直线的距离
2.在生物实验课上,老师布置了“测量锥形瓶内部底面内径”的任务.小亮同学想到了以下这个方案:如图,用螺丝钉将两根小棒AD,BC的中点O固定,利用全等三角形的性质,只要测得C,D之间的距离,就可知道内径AB的长度.此方案中,判定△AOB和△DOC是全等三角形的依据是( )
A. SSS B. SAS C. ASA D. AAS
3.如图①是某种型号拉杆箱的实物图,如图②是它的示意图,行李箱的侧面可看成一个矩形,点F,C,D在同一条直线上,为了拉箱时的舒适度,现将∠ABD调整为75°,若∠D保持不变,则图中∠ECF应( )
A. 减少20° B. 减少10° C. 增加20° D. 增加10°
4.若关于x的不等式ax-b>0的解集为x<,则关于x的不等式(a+b)x>b-a的解集是( )
A. B. C. D.
二、填空题:本题共8小题,每小题5分,共40分。
5.一只杯子静止在斜面上,其受力分析如图所示,重力G的方向竖直向下,支持力N的方向与斜面垂直,摩擦力F的方向与斜面平行.若摩擦力F与重力G方向的夹角∠1的度数为118°,则斜面的坡角∠2的度数为______°.
6.如图,已知△ABC≌△ADE,点D在BC边上,∠CAE=40°,则∠ABC的度数是______.
7.如图,在△ABC中,高线AD和角平分线BE相交于点F.已知△BDF≌△ADC,求∠C的度数______.
8.若关于x的方程的解为正数,则m的取值范围是______.
9.已知∠A的两边与∠B的两边分别垂直,且∠A比∠B的4倍少30°,则∠A= ______°.
10.定义:一个三角形的一边长是另一边长的2倍,这样的三角形叫作“倍长三角形”.若△ABC是“倍长三角形”,有两条边的长分别为2和3,则第三条边的长为______.
11.已知关于x的不等式组的所有整数解的和为-9,m的取值范围是______.
12.目前我国新能源汽车发展迅速,汽车智能辅助驾驶已得到广泛应用,其自动刹车的工作原理是用雷达测出车辆与前方障碍物之间的距离(并结合车速转化为所需时间)如图所示,当此距离等于报警距离时就开始报警提醒,等于危险距离时就自动刹车,现将报警时间划分为4段,分别为准备时间t0,人的反应时间t1,系统反应时间t2,制动时间t3,相应的距离分别为d0,d1,d2,d3,在制动刹车前汽车以速度v(米/秒)匀速运动,通过大数据统计分析得到如表一信息(其中系数k随地面湿滑程度等路面情况而变化,1≤k≤2)
阶段 0.准备 1.人的反应 2.系统反应 3.制动
时间 t0 t1=0.8秒 t2=0.2砂 t3
距离 d0=10米 d1 d2 d3=米
若要求汽车不论在何种路面情况下行驶,报警距离均小于60米,则汽车的行驶速度v应限制在______米/秒以下.
三、解答题:本题共4小题,共40分。解答应写出文字说明,证明过程或演算步骤。
13.(本小题10分)
(1)解下列不等式;
(2)解不等式组,并写出它的整数解.
14.(本小题10分)
为了丰富同学们的业余生活和培养同学们学习数学的兴趣,学校每年会举行一系列的数学文化节活动,为此学校计划购买A、B两种文化节的奖品作为纪念品.已知购买1件A种奖品与2件B种奖品共需要70元,购买2件A种奖品与3件B种奖品共需要120元.
(1)求A种奖品和B种奖品的单价分别为多少元?
(2)学校计划购买A种奖品和B种奖品共200件,总费用不超过5000元,那么最多能购买A种奖品多少件?
15.(本小题10分)
“抖空竹”是国家级非物质文化遗产.“抖空竹”的一个瞬间如图1所示,将图1抽象成一个数学问题:
(1)如图2,若AB∥|CD,∠EAB=75°,∠ECD=110°,求∠E的度数.
(2)已知AB∥CD,点E为AB,CD之外任意一点.
①如图3,探究∠BED与∠B,∠D之间的数量关系,请直接写出结果;
②如图4,探究∠CDE与∠B,∠BED之间的数量关系,请直接写出结果.
16.(本小题10分)
如图1,等边△ABC与等边△ECD的顶点B,C,D三点在一条直线上,连接AD,BE,两线相交于点F.
(1)求∠BFD的度数;
(2)如图2,连接FC,
①求证:FB是∠AFC的平分线;
②若AF=4,CF=2,求BF的长度.
1.【答案】C
2.【答案】B
3.【答案】C
4.【答案】A
5.【答案】28
6.【答案】70°
7.【答案】67.5°
8.【答案】m>-1且m≠1
9.【答案】10或138
10.【答案】1.5或4
11.【答案】3≤m<6或-6≤m<-3
12.【答案】25
13.【答案】x;
-4≤x<,整数解为-4,-3,-2,-1,0.
14.【答案】A种奖品的单价是30元,B种奖品的单价是20元;
最多能购买A种奖品100件.
15.【答案】35°;
①∠BED=∠D-∠B;②∠B=∠BED+∠CDE.
16.【答案】120°;
①见解析;
②6.
第1页,共1页
同课章节目录
