2024-2025学年上海市浦东新区周浦实验学校八年级(下)月考数学试卷(5月份)(含答案)
文档属性
| 名称 | 2024-2025学年上海市浦东新区周浦实验学校八年级(下)月考数学试卷(5月份)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 91.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 00:00:00 | ||
图片预览



文档简介
2024-2025学年上海市浦东新区周浦实验学校八年级(下)月考数学试卷(5月份)
一、选择题:本题共6小题,每小题3分,共18分。在每小题给出的选项中,只有一项是符合题目要求的。
1.一次函数y=2x-3的图象不经过的象限是( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2.如图, ABCD的对角线AC与BD相交于点O,则下列结论一定正确的是( )
A. AB=BC
B. AD=BC
C. OA=OB
D. AC⊥BD
3.如图,O是坐标原点,菱形ABOC的顶点B在x轴的负半轴上,顶点C的坐标为(3,4),则顶点A的坐标为( )
A. (-4,2)
B. (-,4)
C. (-2,4)
D. (-4,)
4.甲乙两人各自加工120个零件,甲由于个人原因没有和乙同时进行,乙先加工30分钟后,甲开始加工.甲为了追赶上乙的进度,加工的速度是乙的1.2倍,最后两人同时完成.求乙每小时加工零件多少个?设乙每小时加工x个零件,可列方程为( )
A. -=30 B. -=30 C. -= D. -=
5.如图,小程的爸爸用一段10m长的铁丝网围成一个一边靠墙(墙长5.5m)的矩形鸭舍,其面积为15m2,在鸭舍侧面中间位置留一个1m宽的门(由其它材料制成),则BC长为( )
A. 5m或6m B. 2.5m或3m C. 5m D. 3m
6.如图,P点为矩形ABCD两对角线的交点,将P点分别以AD、BC为对称轴画出对称点Q、R,形成六边形QABRCD.若AB=2,AD=4,则六边形QABRCD的周长为何?( )
A. 12
B. 4+2
C. 4+4
D. 4+4
二、填空题:本题共12小题,每小题3分,共36分。
7.将直线y=2x向上平移3个单位长度后经过点(1,m),则m的值为______.
8.点A(1,y1),B(2,y2)在直线y=-6x+5的上,则y1 ______y2(用“<”,“=”或“>”填空).
9.已知关于x的分式方程有增根,那么m的值是______.
10.方程的解为______.
11.一项工程,若甲、乙两个工程队合作8天可以完成,甲工程队单独做24天可以完成,则乙工程队单独做需要______天可以完成.
12.如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=10,则EF的长为______.
13.一个正n边形的一个外角是60°,那么n=______.
14.如图,在矩形ABCD中,AB=4,BC=7,AE平分∠BAD,则DE的长为______.
15.如图,菱形ABCD的对角线AC,BD相交于点O,E是AB的中点,连接OE.若OE=2,则菱形的周长为______.
16.在平面直角坐标系中,正方形ABCD的边AD在y轴正半轴上,边BC在第一象限,且点A(0,3)、B(5,3),将正方形ABCD绕点A顺时针旋转α(0°<α<180°),若点B的对应点B′恰好落在坐标轴上,则点C的对应点C′的坐标为____________________.
17.如图,在△ABC中,点D在BC上,BD=2CD,设,那么= ______.(用向量、表示)
18.正方形ABCD的边长是8cm,点M在BC边上,且MC=2cm,P是正方形边上的一个动点,连接PB,当PB=AM时,PC的长是______.
三、解答题:本题共7小题,共56分。解答应写出文字说明,证明过程或演算步骤。
19.(本小题8分)
解方程:.
20.(本小题8分)
解方程组:.
21.(本小题8分)
如图,已知两个不平行的向量和向量.分别用两种不同的方法作出:.
22.(本小题8分)
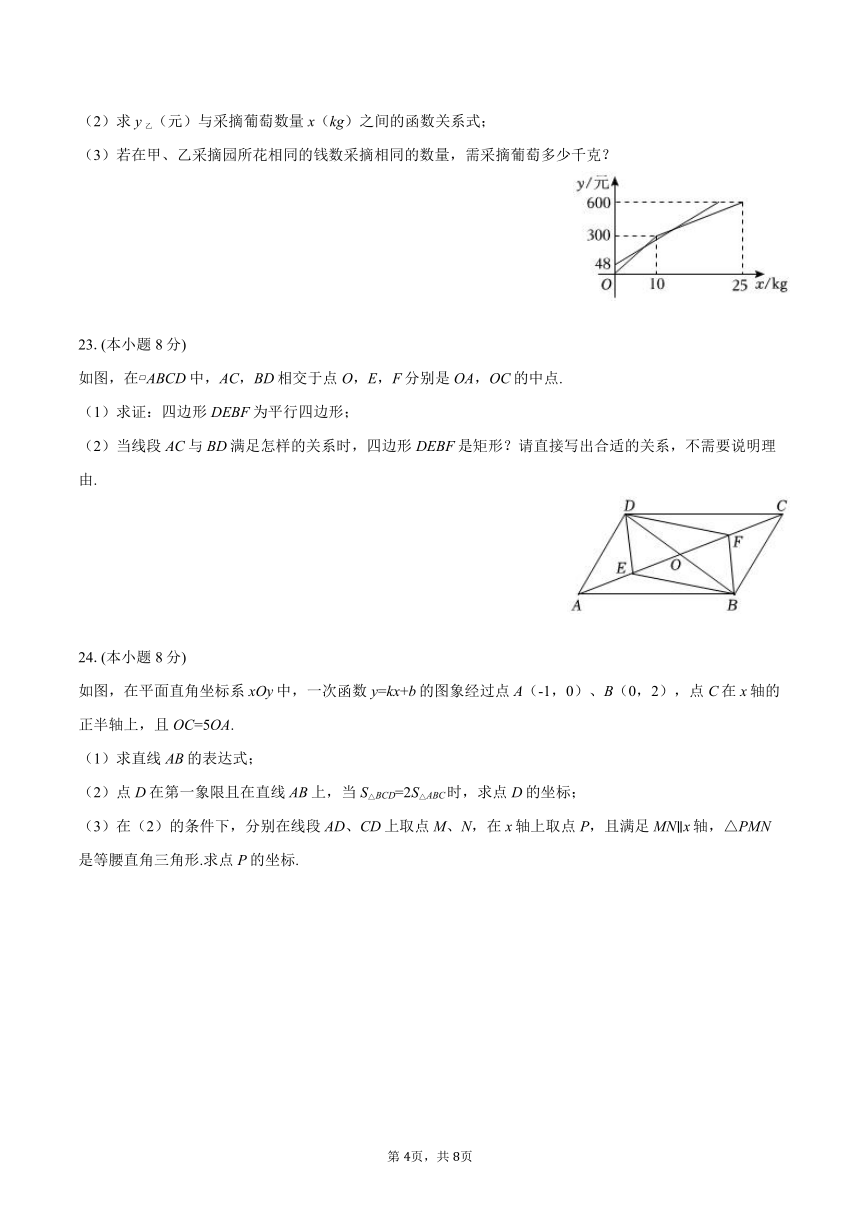
4月中旬的某一天,小明和小强准备去双阳奢岭葡萄采摘园采摘葡萄,甲采摘园的优惠方案:游客进园需购买门票,采摘的所有葡萄按24元/千克;乙采摘园的优惠方案:游客无需买票,采摘葡萄超过一定数量后,超过的部分打折销售.活动期间,某游客的葡萄采摘量为x kg,若在甲采摘园所需总费用为y甲元,若在乙采摘园所需总费用为y乙元,y甲、y乙与x之间的函数图象如图所示.
(1)甲采摘园的门票费用是______元;
(2)求y乙(元)与采摘葡萄数量x(kg)之间的函数关系式;
(3)若在甲、乙采摘园所花相同的钱数采摘相同的数量,需采摘葡萄多少千克?
23.(本小题8分)
如图,在 ABCD中,AC,BD相交于点O,E,F分别是OA,OC的中点.
(1)求证:四边形DEBF为平行四边形;
(2)当线段AC与BD满足怎样的关系时,四边形DEBF是矩形?请直接写出合适的关系,不需要说明理由.
24.(本小题8分)
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象经过点A(-1,0)、B(0,2),点C在x轴的正半轴上,且OC=5OA.
(1)求直线AB的表达式;
(2)点D在第一象限且在直线AB上,当S△BCD=2S△ABC时,求点D的坐标;
(3)在(2)的条件下,分别在线段AD、CD上取点M、N,在x轴上取点P,且满足MN∥x轴,△PMN是等腰直角三角形.求点P的坐标.
25.(本小题8分)
如图,在四边形ABCD中,AD∥BC,∠B=90°,且AD=12cm,AB=8cm,DC=10cm,若动点P从A点出发,以每秒2cm的速度沿线没AD向点D运动;动点Q从C点出发以每秒3cm的速度沿CB向B点运动.当P点到达D点时,动点P,Q同时停止运动,设点P,Q同时出发,并运动了t秒,回答下列问题:
(1)BC= ______cm;
(2)当t= ______秒时,四边形PQBA成为矩形;
(3)当t为多少时,PQ=CD?
1.【答案】B
2.【答案】B
3.【答案】C
4.【答案】D
5.【答案】C
6.【答案】D
7.【答案】5
8.【答案】>
9.【答案】2
10.【答案】x=-2
11.【答案】12
12.【答案】2.5
13.【答案】6
14.【答案】5
15.【答案】16
16.【答案】(7,4)或(5,-2)或(-1,-4)
17.【答案】
18.【答案】2cm或6cm
19.【答案】x=3.
20.【答案】.
21.【答案】如图,,即为所求.
22.【答案】48;
;
8千克或13千克.
23.【答案】见解析;
当AC=2BD时,四边形DEBF是矩形.
24.【答案】y=2x+2;
点D(1,4);
存在,点M的坐标为(,)或(-,).
25.【答案】(1)18;
(2) ;
(3)①当P'Q'∥CD时,如图,
∵AD∥BC,
∴四边形CDP'Q'是平行四边形,
∴P'Q'=CD,DP'=CQ',
∴12-2t=3t,
∴t=,
②如图,梯形PDCQ是等腰梯形时,PQ=CD,
过点P作PF⊥BC于点F,
∴∠PFE=90°,
∵DE⊥BC,
∴∠DEF=90°,
∵AD∥BC,
∴∠EDP=90°,
∴四边形PDEF是矩形,
∴EF=DP=12-2t,
在Rt△CDE和Rt△QPF中,
,
∴Rt△CDE≌Rt△QPF(HL),
∴FQ=CE=6,
∴CQ=FQ+EF+CE=6+12-2t+6=3t,
∴t=.
综上所述:当t为或时,PQ=CD.
第1页,共1页
一、选择题:本题共6小题,每小题3分,共18分。在每小题给出的选项中,只有一项是符合题目要求的。
1.一次函数y=2x-3的图象不经过的象限是( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
2.如图, ABCD的对角线AC与BD相交于点O,则下列结论一定正确的是( )
A. AB=BC
B. AD=BC
C. OA=OB
D. AC⊥BD
3.如图,O是坐标原点,菱形ABOC的顶点B在x轴的负半轴上,顶点C的坐标为(3,4),则顶点A的坐标为( )
A. (-4,2)
B. (-,4)
C. (-2,4)
D. (-4,)
4.甲乙两人各自加工120个零件,甲由于个人原因没有和乙同时进行,乙先加工30分钟后,甲开始加工.甲为了追赶上乙的进度,加工的速度是乙的1.2倍,最后两人同时完成.求乙每小时加工零件多少个?设乙每小时加工x个零件,可列方程为( )
A. -=30 B. -=30 C. -= D. -=
5.如图,小程的爸爸用一段10m长的铁丝网围成一个一边靠墙(墙长5.5m)的矩形鸭舍,其面积为15m2,在鸭舍侧面中间位置留一个1m宽的门(由其它材料制成),则BC长为( )
A. 5m或6m B. 2.5m或3m C. 5m D. 3m
6.如图,P点为矩形ABCD两对角线的交点,将P点分别以AD、BC为对称轴画出对称点Q、R,形成六边形QABRCD.若AB=2,AD=4,则六边形QABRCD的周长为何?( )
A. 12
B. 4+2
C. 4+4
D. 4+4
二、填空题:本题共12小题,每小题3分,共36分。
7.将直线y=2x向上平移3个单位长度后经过点(1,m),则m的值为______.
8.点A(1,y1),B(2,y2)在直线y=-6x+5的上,则y1 ______y2(用“<”,“=”或“>”填空).
9.已知关于x的分式方程有增根,那么m的值是______.
10.方程的解为______.
11.一项工程,若甲、乙两个工程队合作8天可以完成,甲工程队单独做24天可以完成,则乙工程队单独做需要______天可以完成.
12.如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=10,则EF的长为______.
13.一个正n边形的一个外角是60°,那么n=______.
14.如图,在矩形ABCD中,AB=4,BC=7,AE平分∠BAD,则DE的长为______.
15.如图,菱形ABCD的对角线AC,BD相交于点O,E是AB的中点,连接OE.若OE=2,则菱形的周长为______.
16.在平面直角坐标系中,正方形ABCD的边AD在y轴正半轴上,边BC在第一象限,且点A(0,3)、B(5,3),将正方形ABCD绕点A顺时针旋转α(0°<α<180°),若点B的对应点B′恰好落在坐标轴上,则点C的对应点C′的坐标为____________________.
17.如图,在△ABC中,点D在BC上,BD=2CD,设,那么= ______.(用向量、表示)
18.正方形ABCD的边长是8cm,点M在BC边上,且MC=2cm,P是正方形边上的一个动点,连接PB,当PB=AM时,PC的长是______.
三、解答题:本题共7小题,共56分。解答应写出文字说明,证明过程或演算步骤。
19.(本小题8分)
解方程:.
20.(本小题8分)
解方程组:.
21.(本小题8分)
如图,已知两个不平行的向量和向量.分别用两种不同的方法作出:.
22.(本小题8分)
4月中旬的某一天,小明和小强准备去双阳奢岭葡萄采摘园采摘葡萄,甲采摘园的优惠方案:游客进园需购买门票,采摘的所有葡萄按24元/千克;乙采摘园的优惠方案:游客无需买票,采摘葡萄超过一定数量后,超过的部分打折销售.活动期间,某游客的葡萄采摘量为x kg,若在甲采摘园所需总费用为y甲元,若在乙采摘园所需总费用为y乙元,y甲、y乙与x之间的函数图象如图所示.
(1)甲采摘园的门票费用是______元;
(2)求y乙(元)与采摘葡萄数量x(kg)之间的函数关系式;
(3)若在甲、乙采摘园所花相同的钱数采摘相同的数量,需采摘葡萄多少千克?
23.(本小题8分)
如图,在 ABCD中,AC,BD相交于点O,E,F分别是OA,OC的中点.
(1)求证:四边形DEBF为平行四边形;
(2)当线段AC与BD满足怎样的关系时,四边形DEBF是矩形?请直接写出合适的关系,不需要说明理由.
24.(本小题8分)
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象经过点A(-1,0)、B(0,2),点C在x轴的正半轴上,且OC=5OA.
(1)求直线AB的表达式;
(2)点D在第一象限且在直线AB上,当S△BCD=2S△ABC时,求点D的坐标;
(3)在(2)的条件下,分别在线段AD、CD上取点M、N,在x轴上取点P,且满足MN∥x轴,△PMN是等腰直角三角形.求点P的坐标.
25.(本小题8分)
如图,在四边形ABCD中,AD∥BC,∠B=90°,且AD=12cm,AB=8cm,DC=10cm,若动点P从A点出发,以每秒2cm的速度沿线没AD向点D运动;动点Q从C点出发以每秒3cm的速度沿CB向B点运动.当P点到达D点时,动点P,Q同时停止运动,设点P,Q同时出发,并运动了t秒,回答下列问题:
(1)BC= ______cm;
(2)当t= ______秒时,四边形PQBA成为矩形;
(3)当t为多少时,PQ=CD?
1.【答案】B
2.【答案】B
3.【答案】C
4.【答案】D
5.【答案】C
6.【答案】D
7.【答案】5
8.【答案】>
9.【答案】2
10.【答案】x=-2
11.【答案】12
12.【答案】2.5
13.【答案】6
14.【答案】5
15.【答案】16
16.【答案】(7,4)或(5,-2)或(-1,-4)
17.【答案】
18.【答案】2cm或6cm
19.【答案】x=3.
20.【答案】.
21.【答案】如图,,即为所求.
22.【答案】48;
;
8千克或13千克.
23.【答案】见解析;
当AC=2BD时,四边形DEBF是矩形.
24.【答案】y=2x+2;
点D(1,4);
存在,点M的坐标为(,)或(-,).
25.【答案】(1)18;
(2) ;
(3)①当P'Q'∥CD时,如图,
∵AD∥BC,
∴四边形CDP'Q'是平行四边形,
∴P'Q'=CD,DP'=CQ',
∴12-2t=3t,
∴t=,
②如图,梯形PDCQ是等腰梯形时,PQ=CD,
过点P作PF⊥BC于点F,
∴∠PFE=90°,
∵DE⊥BC,
∴∠DEF=90°,
∵AD∥BC,
∴∠EDP=90°,
∴四边形PDEF是矩形,
∴EF=DP=12-2t,
在Rt△CDE和Rt△QPF中,
,
∴Rt△CDE≌Rt△QPF(HL),
∴FQ=CE=6,
∴CQ=FQ+EF+CE=6+12-2t+6=3t,
∴t=.
综上所述:当t为或时,PQ=CD.
第1页,共1页
同课章节目录
