10.1.2垂线及其性质 教学设计(表格式) 沪科版(2024)数学七年级下册
文档属性
| 名称 | 10.1.2垂线及其性质 教学设计(表格式) 沪科版(2024)数学七年级下册 |

|
|
| 格式 | doc | ||
| 文件大小 | 661.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 11:08:00 | ||
图片预览

文档简介
1 相交线
第2课时 垂线及其性质
教学设计
课标摘录 理解垂线、垂线段等概念,能用三角尺或量角器过一点画已知直线的垂线.理解点到直线的距离的意义,能度量点到直线的距离.掌握基本事实:过一点有且只有一条直线与已知直线垂直.
教学目标 1.了解垂线、垂线段等概念,能过一点作已知直线的垂线;理解点到直线的距离的意义,能度量点到直线的距离.2.理解并掌握垂线的两个性质,能利用垂线的定义计算角的度数.3.经历观察、操作、探索、归纳、总结的过程,初步形成几何概念的认识方式和几何结论的归纳方法.4.通过丰富的数学活动,体验数学活动充满着探索和创造,体会数学的应用价值,培养积极思维的学习习惯.
教学重难点 重点:了解垂线、垂线段等概念,能过一点作已知直线的垂线;理解点到直线的距离的意义,能度量点到直线的距离.难点:理解并掌握垂线的两个性质,能利用垂线的定义计算角的度数.
教学策略 通过复习回顾对顶角与邻补角,为讲解垂线做铺垫.便于学生建立起新旧知识之间的联系.学生经历观察、思考,总结出垂线的性质. 让学生感受知识的形成过程,培养学生严谨的科学态度,锻炼学生自主探究学习的能力,激发学生的学习兴趣.
教学过程
教学步骤 教学活动
情境导入 【情景引入】将十字街口的两条道路看作两条直线,如图(2)中的AB和CD,它们相交于点O,形成4个角.如果∠AOC=90°,那么其他3个角的度数各是多少?为什么?分析:由对顶角相等,邻补角互补,可以得出其他3个角都是90°.教学建议:引导学生观察图片,由对顶角与邻补角等相关知识,得出夹角为90°,为后续学习垂线做铺垫.设计意图:通过复习回顾对顶角与邻补角,为讲解垂线做铺垫.便于学生建立起新旧知识之间的联系.
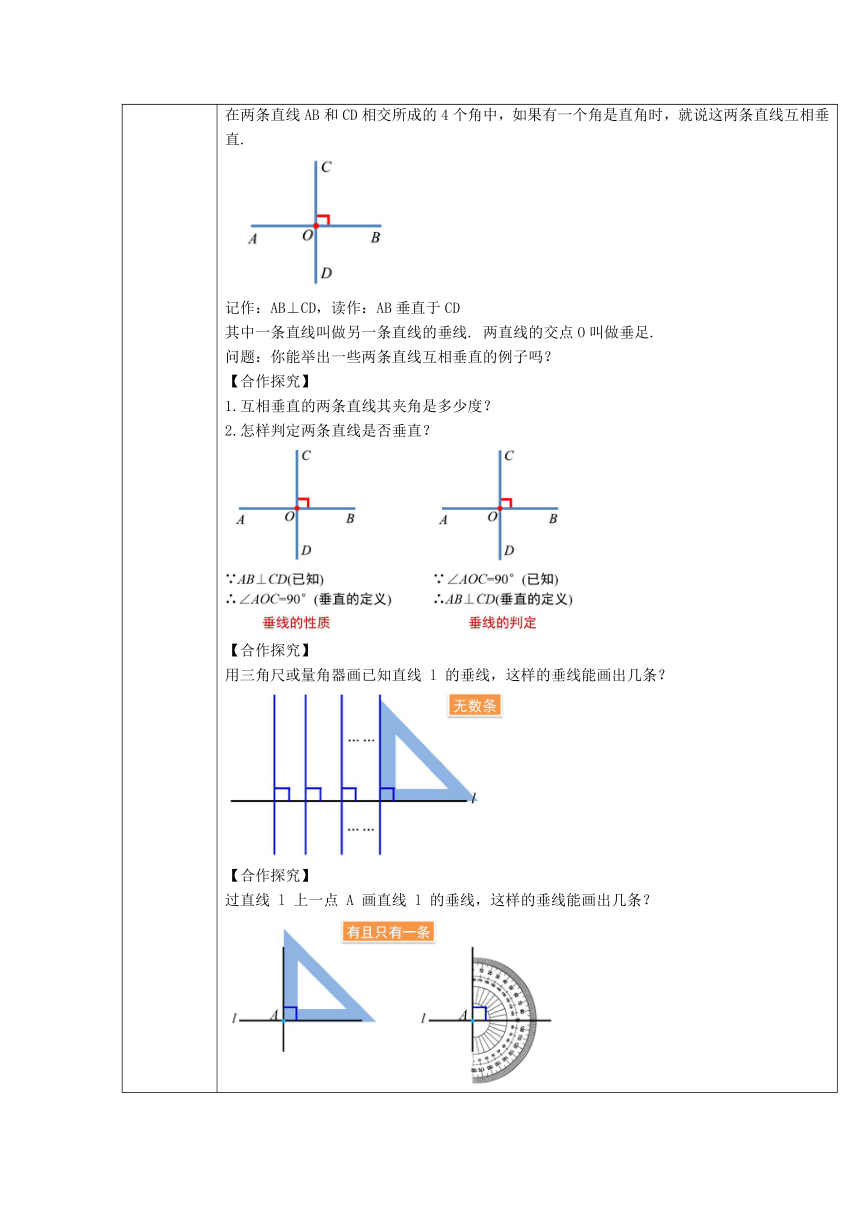
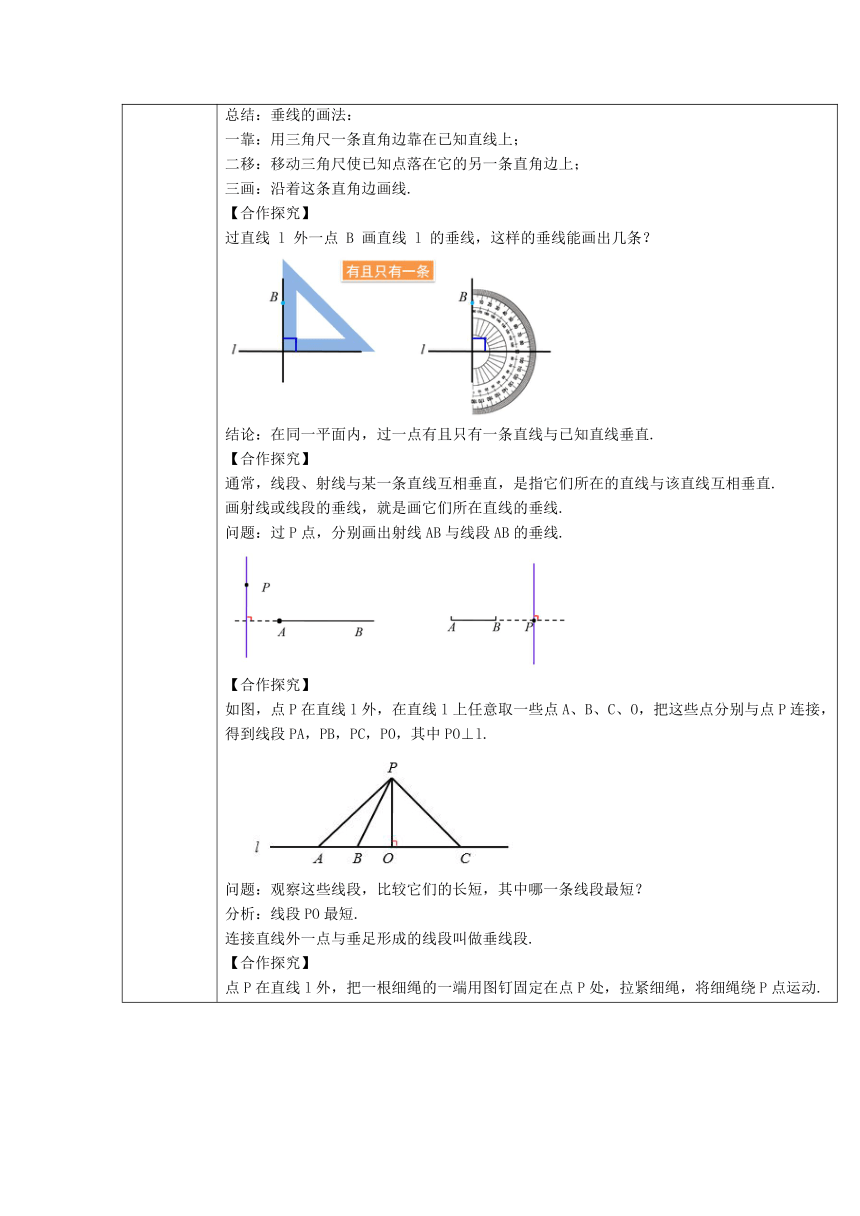
新知初探 归纳:在两条直线AB和CD相交所成的4个角中,如果有一个角是直角时,就说这两条直线互相垂直.记作:AB⊥CD,读作:AB垂直于CD其中一条直线叫做另一条直线的垂线. 两直线的交点O叫做垂足.问题:你能举出一些两条直线互相垂直的例子吗?【合作探究】1.互相垂直的两条直线其夹角是多少度?2.怎样判定两条直线是否垂直?【合作探究】用三角尺或量角器画已知直线 l 的垂线,这样的垂线能画出几条?【合作探究】过直线 l 上一点 A 画直线 l 的垂线,这样的垂线能画出几条?总结:垂线的画法:一靠:用三角尺一条直角边靠在已知直线上;二移:移动三角尺使已知点落在它的另一条直角边上;三画:沿着这条直角边画线.【合作探究】过直线 l 外一点 B 画直线 l 的垂线,这样的垂线能画出几条?结论:在同一平面内,过一点有且只有一条直线与已知直线垂直.【合作探究】通常,线段、射线与某一条直线互相垂直,是指它们所在的直线与该直线互相垂直.画射线或线段的垂线,就是画它们所在直线的垂线. 问题:过P点,分别画出射线AB与线段AB的垂线.【合作探究】如图,点P在直线l外,在直线l上任意取一些点A、B、C、O,把这些点分别与点P连接,得到线段PA,PB,PC,PO,其中PO⊥l.问题:观察这些线段,比较它们的长短,其中哪一条线段最短?分析:线段PO最短.连接直线外一点与垂足形成的线段叫做垂线段.【合作探究】点P在直线l外,把一根细绳的一端用图钉固定在点P处,拉紧细绳,将细绳绕P点运动.问题:根据标记点O位置的变化,你有什么发现?归纳:垂线段:连接直线外一点与垂足形成的线段叫做垂线段.垂线段的性质:在连接直线外一点与直线上各点的所有线段中,垂线段最短.点到直线的距离:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.教学建议:引导学生思考探究,小组合作交流,归纳总结出垂线的相关概念与性质设计意图:学生经历观察、思考,总结出垂线的性质. 让学生感受知识的形成过程,培养学生严谨的科学态度,锻炼学生自主探究学习的能力,激发学生的学习兴趣.
【典型例题】例1 如图,∠ACB=90°,CD⊥AB,线段AC、BC、CD中最短的是( )A. AC B. BC C. CD D. 无法确定例2 如图,直线 AB、CD相交于点O,OE⊥AB,∠AOD=125°,求∠COE的度数.解:∵∠AOD=125°又∵∠COB=∠AOD∴∠COB=125°∵OE⊥AB∴∠EOB=90°∵∠COE=∠COB-∠EOB∴∠COE=125°-90°=35°【教学建议】教师适当引导,学生自主完成.设计意图:通过例题,规范学生对解题步骤的书写,让学生感受数学的严谨性.
当堂达标 1. 如图,在三角形ABC中,D是BC中点,连接AD,请分别画出自点B,C向AD所作的垂线(垂足为E,F).2. (1)如图,用三角尺画出点A到直线BC的垂线段; (2)画出点B到直线AC的垂线段.3. 如图,直线l表示一条公路,点P是一所学校所在的位置,要修一条从学校到公路的道路,如何修才能使道路最短?画出所修道路的示意图.【教学建议】教师给出练习,随时观察学生完成情况并给与指导,根据学生完成情况适当分析讲解.设计意图:进一步巩固本节课的内容. 了解学习效果,让学生经历运用知识解决问题的过程,给学生获得成功体验的空间.
课堂小结 以思维导图的形式呈现本节课所讲解的内容.教学建议:教师可以提问学生总结所学内容,提高学生的总结能力和表达能力.设计意图:通过小结,让学生进一步熟悉巩固本节课所学的知识,帮助学生把握知识要点,理清知识脉络.
板书设计
教学反思 本节课做到了“有序”与“和谐”的课堂教学追求.“有序”反映在课程目标指向明确,从生活中常见的情境入手,即抽取学生生活中的实例,激活学生已有的知识基础,进而学习“垂直”的位置关系;教学设计主线清晰,即先“近距离”生活导入,显现熟知概念“互相”,再“近距离”经验展开,突破核心概念“互相垂直”,其次“净用”教具操作,深化内涵理解,然后“进入”网状架构,强化认知水准.“和谐”不仅体现教学环节设计所兼顾的数学性与生活性,体现了师生互动(生生互动)的及时性与生成性,还体现了教者对学生知识检测的准确性与全面性,更体现了学生对“垂直”概念的理解与操作运用的融合性.
10.1.2垂线及其性质
1.垂线的定义: 例2 如图,直线 AB、CD相交于点O,OE⊥AB,∠AOD=125°,求∠COE的度数。
2.垂线段:
3.点到直线的距离:
4.垂线的性质:
性质1: 性质2:
第2课时 垂线及其性质
教学设计
课标摘录 理解垂线、垂线段等概念,能用三角尺或量角器过一点画已知直线的垂线.理解点到直线的距离的意义,能度量点到直线的距离.掌握基本事实:过一点有且只有一条直线与已知直线垂直.
教学目标 1.了解垂线、垂线段等概念,能过一点作已知直线的垂线;理解点到直线的距离的意义,能度量点到直线的距离.2.理解并掌握垂线的两个性质,能利用垂线的定义计算角的度数.3.经历观察、操作、探索、归纳、总结的过程,初步形成几何概念的认识方式和几何结论的归纳方法.4.通过丰富的数学活动,体验数学活动充满着探索和创造,体会数学的应用价值,培养积极思维的学习习惯.
教学重难点 重点:了解垂线、垂线段等概念,能过一点作已知直线的垂线;理解点到直线的距离的意义,能度量点到直线的距离.难点:理解并掌握垂线的两个性质,能利用垂线的定义计算角的度数.
教学策略 通过复习回顾对顶角与邻补角,为讲解垂线做铺垫.便于学生建立起新旧知识之间的联系.学生经历观察、思考,总结出垂线的性质. 让学生感受知识的形成过程,培养学生严谨的科学态度,锻炼学生自主探究学习的能力,激发学生的学习兴趣.
教学过程
教学步骤 教学活动
情境导入 【情景引入】将十字街口的两条道路看作两条直线,如图(2)中的AB和CD,它们相交于点O,形成4个角.如果∠AOC=90°,那么其他3个角的度数各是多少?为什么?分析:由对顶角相等,邻补角互补,可以得出其他3个角都是90°.教学建议:引导学生观察图片,由对顶角与邻补角等相关知识,得出夹角为90°,为后续学习垂线做铺垫.设计意图:通过复习回顾对顶角与邻补角,为讲解垂线做铺垫.便于学生建立起新旧知识之间的联系.
新知初探 归纳:在两条直线AB和CD相交所成的4个角中,如果有一个角是直角时,就说这两条直线互相垂直.记作:AB⊥CD,读作:AB垂直于CD其中一条直线叫做另一条直线的垂线. 两直线的交点O叫做垂足.问题:你能举出一些两条直线互相垂直的例子吗?【合作探究】1.互相垂直的两条直线其夹角是多少度?2.怎样判定两条直线是否垂直?【合作探究】用三角尺或量角器画已知直线 l 的垂线,这样的垂线能画出几条?【合作探究】过直线 l 上一点 A 画直线 l 的垂线,这样的垂线能画出几条?总结:垂线的画法:一靠:用三角尺一条直角边靠在已知直线上;二移:移动三角尺使已知点落在它的另一条直角边上;三画:沿着这条直角边画线.【合作探究】过直线 l 外一点 B 画直线 l 的垂线,这样的垂线能画出几条?结论:在同一平面内,过一点有且只有一条直线与已知直线垂直.【合作探究】通常,线段、射线与某一条直线互相垂直,是指它们所在的直线与该直线互相垂直.画射线或线段的垂线,就是画它们所在直线的垂线. 问题:过P点,分别画出射线AB与线段AB的垂线.【合作探究】如图,点P在直线l外,在直线l上任意取一些点A、B、C、O,把这些点分别与点P连接,得到线段PA,PB,PC,PO,其中PO⊥l.问题:观察这些线段,比较它们的长短,其中哪一条线段最短?分析:线段PO最短.连接直线外一点与垂足形成的线段叫做垂线段.【合作探究】点P在直线l外,把一根细绳的一端用图钉固定在点P处,拉紧细绳,将细绳绕P点运动.问题:根据标记点O位置的变化,你有什么发现?归纳:垂线段:连接直线外一点与垂足形成的线段叫做垂线段.垂线段的性质:在连接直线外一点与直线上各点的所有线段中,垂线段最短.点到直线的距离:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.教学建议:引导学生思考探究,小组合作交流,归纳总结出垂线的相关概念与性质设计意图:学生经历观察、思考,总结出垂线的性质. 让学生感受知识的形成过程,培养学生严谨的科学态度,锻炼学生自主探究学习的能力,激发学生的学习兴趣.
【典型例题】例1 如图,∠ACB=90°,CD⊥AB,线段AC、BC、CD中最短的是( )A. AC B. BC C. CD D. 无法确定例2 如图,直线 AB、CD相交于点O,OE⊥AB,∠AOD=125°,求∠COE的度数.解:∵∠AOD=125°又∵∠COB=∠AOD∴∠COB=125°∵OE⊥AB∴∠EOB=90°∵∠COE=∠COB-∠EOB∴∠COE=125°-90°=35°【教学建议】教师适当引导,学生自主完成.设计意图:通过例题,规范学生对解题步骤的书写,让学生感受数学的严谨性.
当堂达标 1. 如图,在三角形ABC中,D是BC中点,连接AD,请分别画出自点B,C向AD所作的垂线(垂足为E,F).2. (1)如图,用三角尺画出点A到直线BC的垂线段; (2)画出点B到直线AC的垂线段.3. 如图,直线l表示一条公路,点P是一所学校所在的位置,要修一条从学校到公路的道路,如何修才能使道路最短?画出所修道路的示意图.【教学建议】教师给出练习,随时观察学生完成情况并给与指导,根据学生完成情况适当分析讲解.设计意图:进一步巩固本节课的内容. 了解学习效果,让学生经历运用知识解决问题的过程,给学生获得成功体验的空间.
课堂小结 以思维导图的形式呈现本节课所讲解的内容.教学建议:教师可以提问学生总结所学内容,提高学生的总结能力和表达能力.设计意图:通过小结,让学生进一步熟悉巩固本节课所学的知识,帮助学生把握知识要点,理清知识脉络.
板书设计
教学反思 本节课做到了“有序”与“和谐”的课堂教学追求.“有序”反映在课程目标指向明确,从生活中常见的情境入手,即抽取学生生活中的实例,激活学生已有的知识基础,进而学习“垂直”的位置关系;教学设计主线清晰,即先“近距离”生活导入,显现熟知概念“互相”,再“近距离”经验展开,突破核心概念“互相垂直”,其次“净用”教具操作,深化内涵理解,然后“进入”网状架构,强化认知水准.“和谐”不仅体现教学环节设计所兼顾的数学性与生活性,体现了师生互动(生生互动)的及时性与生成性,还体现了教者对学生知识检测的准确性与全面性,更体现了学生对“垂直”概念的理解与操作运用的融合性.
10.1.2垂线及其性质
1.垂线的定义: 例2 如图,直线 AB、CD相交于点O,OE⊥AB,∠AOD=125°,求∠COE的度数。
2.垂线段:
3.点到直线的距离:
4.垂线的性质:
性质1: 性质2:
