鲁科版高中物理必修第一册第3章相互作用3.2科学探究:弹力教学课件(共46张PPT)
文档属性
| 名称 | 鲁科版高中物理必修第一册第3章相互作用3.2科学探究:弹力教学课件(共46张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 10.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-08-15 21:12:43 | ||
图片预览










文档简介
(共46张PPT)
第2节 科学探究:弹力 第1课时
第三章 相互作用
学习目标
1.知道形变的概念及类型,知道观察桌面和玻璃瓶的微小形变的方法。
2.知道弹力的概念,知道弹力产生的条件。
3.知道弹力的种类及其方向。
蹦极时,人由于自身所受的重力而下落,被拉伸的蹦极绳会对人产生向上的弹力,把人拉上去,如此上下振荡。
在这个过程中,蹦极绳的弹力与形变发挥了重要作用。
压扁的面包
伸长的橡皮筋
拨动的琴弦
凹陷的沙发
压扁
弯曲
伸长
凹陷
……
都是形状上发生了变化
一辆汽车行驶在大桥上,桥面会产生形变了吗?用手压墙,桥面产生形变了吗?
有些物体的形变明显,容易观察;有些物体的形变却很难直接观察到。对于这些不易直接观察到的微小形变,可借助某些装置来验证其存在
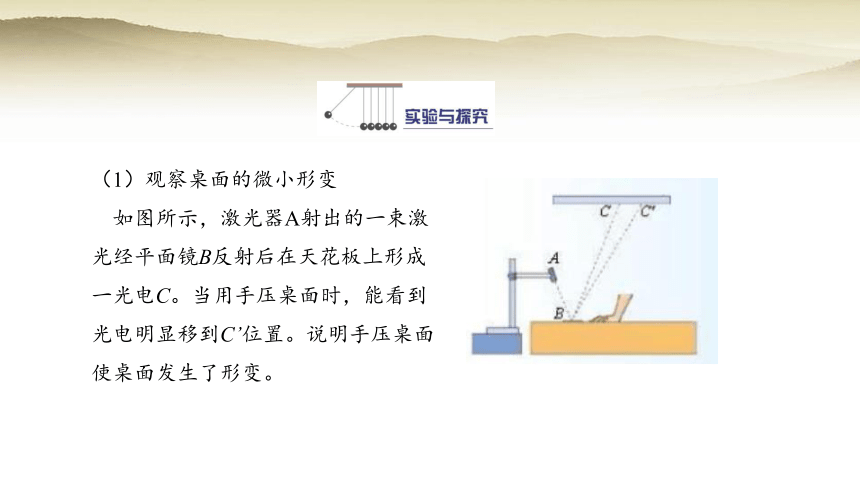
(1)观察桌面的微小形变
如图所示,激光器A射出的一束激光经平面镜B反射后在天花板上形成一光电C。当用手压桌面时,能看到光电明显移到C’位置。说明手压桌面使桌面发生了形变。
(2)观察玻璃瓶的微小形变
在扁平玻璃瓶中装满水,瓶口用中间插有细玻璃管的软木塞塞紧,这时瓶内的水就会上升到细玻璃管中。如图所示,当用力挤压玻璃瓶的不同部位时,会发现细玻璃管中的水面会上升或下降。这说明玻璃瓶发生了形变。为了便于观察,可给水加色,并将细玻璃管固定在白色纸板上,纸板上可画细刻度线作为参考。
3.形变的种类:
①弹性形变:
某些发生形变的物体在撤去外力后能恢复原状,这种物体称为弹性体,对应的形变称为弹性形变,如波动的琴弦、拉开的弓箭。
②范性形变:
有些物体发生形变后不能恢复原状,这种形变称为范性形变,如压扁的面包、橡皮泥。
4.弹性限度:弹性体的形变不能无限增大,若超过一定的限度,撤去外力时物体就不能恢复原状,这个限度称为弹性限度。
弹簧被压缩,产生了形变,球被弹出去,说明有力的作用,这个力我们叫什么呢?
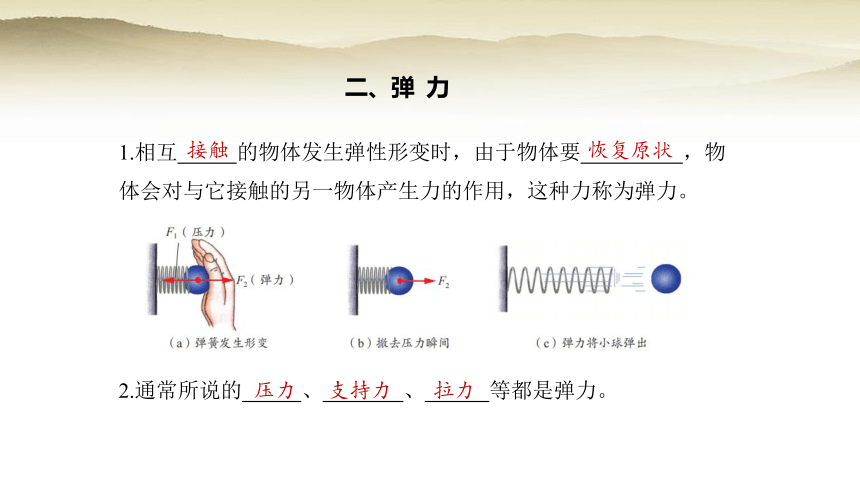
1.相互 的物体发生弹性形变时,由于物体要 ,物体会对与它接触的另一物体产生力的作用,这种力称为弹力。
2.通常所说的 、 、 等都是弹力。
接触
恢复原状
压力
支持力
拉力
二、弹 力
是不是所有的形变都能产生弹力呢?
3.弹力的产生条件:
①物体间相互接触
②物体间发生弹性形变
只有弹性形变产生的力才能叫做弹力。 因为只有撤去外力,物体为恢复到原来形状的而产生的力才叫作"弹力"
一铁块放在海绵上,铁块和海绵都发生了形变,从而在它们之间产生了弹力,如图所示。海绵对铁块的支持力是如何产生的?铁块对海绵的压力是怎样产生的?
铁块对海绵的压力是铁块发生了弹性形变,对与它接触的海绵产生力的作用(如图乙)。
海绵对铁块的支持力是海绵发生弹性形变,对与它接触的铁块产生力的作用(如图甲)。
(1)只有相互接触的物体间才可能有弹力。( )
(2)发生形变后的物体撤去外力后都能恢复原状。( )
(3)静止在水平地面上的物体受到向上的弹力是因为地面发生了形变。 ( )
(4)海绵受挤压会发生形变,桌面受挤压不会发生形变。( )
√
×
√
×
关于四种与足球有关的情境,下列说法正确的是( )
A.图甲,静止在草地上的足球对地面的压力就是它的重力
B.图乙,静止在水平地面上的两个足球间一定有弹力
C.图丙,踩在脚下且静止在地面上的足球一定只受一个弹力的作用
D.图丁,打到球网上的足球受到弹力是因为球网发生了形变
D
4.弹力的方向
(1)弹力方向 。
(2)几种常见弹力方向判断
绳子对物体拉力的方向总是沿着绳子而指向绳子收缩的方向
压力的方向总是垂直于接触面,指向被压的物体.
支持力的方向总是垂直支持面,指向被支持的物体.
FN
FT
FT1
FT2
F压
物块
桌面
小球
总是与物体形变的方向相反
(多选)关于弹力的方向,以下说法不正确的是( )
A.轻杆对物体的弹力方向总是沿着杆,并指向杆收缩的方向
B.轻绳对物体拉力的方向总是沿着绳,并指向绳收缩的方向
C.弹簧对物体的弹力方向,与弹簧形变的方向相同
D.物体受到的支持力的方向总是垂直于支持面,并指向被支持物体
AC
画出右面各物体所受弹力的示意图。
(1)图(a)中杆AB斜靠在半球体上静止,作出AB杆所受弹力的示意图。
(2)图(b)中用绳子将球挂在墙壁上,作出球所受弹力的示意图。
(3)图(c)中竖直悬挂在细绳上的光滑小球与斜面刚好接触而保持静止,作出小球所受弹力的示意图。
N1
N
N2
N1
N2
5.弹力有无的判断
条件法
拆除法
假设法
效果法
接触并发生形变
假设把与物体去掉,看能否维持原状
假设存在弹力,判断是否保持原状
有弹力,则该弹力必有相应的作用效果
(多选)在下列图中,a、b表面均光滑,且a、b均处于静止状态,天花板和地面均水平,A、D选项中细绳均竖直。a、b间一定有弹力的是( )
BC
第2节 科学探究:弹力 第2课时
第三章 相互作用
学习目标
1.能完成实验“探究弹簧弹力的大小与伸长量的关系”。
2.掌握胡克定律,并能用胡克定律进行简单的计算。
弹簧弹力的大小与形变量有什么关系呢?
提出问题
大胆猜想
弹簧弹力的大小与弹簧的形变量成正比
设计实验
实验:探究弹簧弹力的大小与伸长量的关系 胡克定律
1.实验目的
(1)探究弹簧弹力的大小与伸长量的关系。
(2)了解弹簧测力计的工作原理。
2.实验器材
铁架台、带挂钩的弹簧、钩码、
3.实验原理与设计
(1)将已知质量的钩码悬挂于弹簧上,由二力平衡可知,弹簧对钩码的弹力大小 钩码所受重力的大小。 F=G
(2)通过改变悬挂的钩码 来改变弹簧弹力的大小,测出弹簧未挂钩码时的 及挂钩码后的长度,可得出挂不同数量钩码情况下弹簧的 。
(3)由此可进一步得出弹簧弹力的大小与弹簧伸长量的关系。
等于
个数
长度(弹簧原长)
伸长量
4.实验步骤
(1)安装实验装置。
(2)用刻度尺测量弹簧原长。
(3)在弹簧挂钩上依次挂不同数量的钩码,并分别记下实验所挂钩码的总质量及弹簧长度。
次数 1 2 3 4 5
钩码质量m/g
弹簧弹力F/N
弹簧长度l/cm
弹簧伸长量x/cm
0
0
10.95
0
1.85
12.80
0.5
50
100
1.0
14.65
3.70
5.60
16.55
1.5
150
200
2.0
18.40
7.45
5.数据分析
(1)将数据及计算结果填入表中。
弹簧弹力的大小与伸长量的关系
(2)在坐标纸上作出弹簧弹力大小随伸长量变化的图像,并进行分析讨论。
弹簧弹力
F(N) 0 0.5 1.0 1.5 2.0
弹簧形变量x(cm) 0 1.85 3.70 5.60 7.45
F/N
x/cm
0
×
×
×
×
×
0.5
1.0
2.0
1.5
2.5
3.0
1
2
3
4
5
6
7
8
6.实验结论
(1)弹簧的弹力随伸长量的增大而 。
(2)在误差允许范围内,弹簧的弹力大小与 成正比。
增大
伸长量
用F表示
用x表示
(1)尽量选轻质弹簧以减小弹簧 带来的影响。
(2)实验中弹簧下端挂的钩码不要太多,避免 。
(3)测量长度时,应区别弹簧原长l0、实际长度l及形变量x三者之间的不同,明确三者之间的关系。为了减小弹簧自身重力带来的影响,测弹簧原长时应让弹簧在 时保持自由下垂状态,而不是平放在水平面上处于自然伸长状态。
7.注意事项
自身重力
超出弹簧的弹性限度
不挂钩码
(4)记录数据时要注意弹簧的弹力及形变量的对应关系及单位。
(5)描点作图时,应使尽量多的点落在画出的线上,可允许少数点均匀分布于线两侧,偏离太大的点应舍去,描出的线不应是折线,而应是平滑的曲线或直线。
在“探究弹簧弹力与形变量的关系”的实验中。
(1)下列实验步骤是甲同学准备完成的,请你帮他按正确操作的先后顺序,将各步骤前的字母写在横线上 。
A.以弹簧伸长量为横坐标,以弹力大小为纵坐标,描出各组数据(x,F)对应的点,并用平滑的曲线连接起来;
B.将铁架台固定于桌子上,并将弹簧的一端系于横梁上,在弹簧附近竖直固定一把刻度尺;
C.记下弹簧不挂钩码时,其下端对应的刻度l0;
D.依次在弹簧下端挂上1个、2个、3个、…、n个钩码,并分别记下钩码静止时,弹簧下端所对应的刻度并记录在表格内,然后取下钩码;
E.以弹簧伸长量为自变量,写出弹力的大小与弹簧伸长量的关系式;
F.解释函数表达式中常数的物理意义。
BCDAEF
(2)乙同学在做实验过程中,先把弹簧平放在桌面上使其自然伸长,用直尺测出弹簧的原长l0,再把弹簧竖直悬挂起来,挂上钩码后测出弹簧伸长后的长度L,把(L-l0)作为弹簧的伸长量x,由于弹簧自身重力的影响,这样操作最后画出的图线可能是____。
C
(3)如图是丙同学按正确步骤完成实验并画出弹簧弹力的大小和弹簧形变量的关系图线。写出该图线的函数表达式:____________。
F=0.43x(N)
如图所示,你能根据图像求出表达式F=kx中的比例系数k吗?它是什么物理量?
3.50
3.00
2.50
2.00
1.50
1.00
0.50
(0,0)
(13.6,3.5)
k为弹簧的劲度系数
胡克 英国科学家
(1635——1703)
胡克定律
1.内容:在弹性限度内,弹簧弹力F的大小
跟 成正比,即F= 。
2.劲度系数:式中的比例系数k称为弹簧的 ,单位是 ,符号是 ,是表示弹簧“软”“硬”程度的物理量。
3.劲度系数与弹性体的 、 等因素有关。
弹簧伸长(或压缩)的长度x
kx
劲度系数
N/m
形状
材料
牛顿每米
1.弹簧的形变量越大,弹力就会越大,若将弹簧拉得很长甚至拉直,还能用胡克定律计算吗?
不能。超出了弹簧的弹性限度,不能再用胡克定律计算了。
2.生活中说有的弹簧 “硬”,有的弹簧 “软”,指的就是它们的劲度系数不同。那弹簧的劲度系数跟哪些因素有关呢?
弹簧的劲度系数k只与弹簧本身有关,由弹簧本身的材料、长度、粗细、匝数等因素决定,它反应了弹簧的软硬程度,与弹力F的大小和形变量x无关。
例题:如图所示,一根轻弹簧长度由原来的5.00 cm伸长为6.00cm时,手受到的弹力为10.0N。那么,当这根弹簧伸长到6.20 cm时(在弹性限度内),手受到的弹力有多大?
C.弹簧的劲度系数k是由弹簧本身的性质决定的,与弹力F的大小和弹簧
形变量x的大小无关
D.弹簧的劲度系数在数值上等于弹簧伸长(或缩短)单位长度时弹力的数值
ACD
2.由实验测得某弹簧所受弹力F和弹簧的长度x的关系图像如图所示,求:
(1)该弹簧的原长;
答案 (1) 6 cm (2) 1 000 N/m
(2)该弹簧的劲度系数。
3.用如图甲所示的装置来探究胡克定律。轻质弹簧的左端与固定在墙上的拉力传感器连接,右端在水平拉力F的作用下从原长开始沿水平方向缓慢伸长,弹簧与水平面不接触,通过刻度尺可以读出弹簧的伸长量x,通过拉力传感器可以读出拉力F,多次测量F、x,作出F-x图像如图乙所示,回答下列问题:
(1)当弹力增大到一定程度时,图像变弯曲,原因什么?
弹簧形变量超出弹簧的弹性限度
(2)弹簧的劲度系数为____;
(3)弹簧的伸长量分别为x2和x1时,拉力传感器的示数之差为_________。
第2节 科学探究:弹力 第1课时
第三章 相互作用
学习目标
1.知道形变的概念及类型,知道观察桌面和玻璃瓶的微小形变的方法。
2.知道弹力的概念,知道弹力产生的条件。
3.知道弹力的种类及其方向。
蹦极时,人由于自身所受的重力而下落,被拉伸的蹦极绳会对人产生向上的弹力,把人拉上去,如此上下振荡。
在这个过程中,蹦极绳的弹力与形变发挥了重要作用。
压扁的面包
伸长的橡皮筋
拨动的琴弦
凹陷的沙发
压扁
弯曲
伸长
凹陷
……
都是形状上发生了变化
一辆汽车行驶在大桥上,桥面会产生形变了吗?用手压墙,桥面产生形变了吗?
有些物体的形变明显,容易观察;有些物体的形变却很难直接观察到。对于这些不易直接观察到的微小形变,可借助某些装置来验证其存在
(1)观察桌面的微小形变
如图所示,激光器A射出的一束激光经平面镜B反射后在天花板上形成一光电C。当用手压桌面时,能看到光电明显移到C’位置。说明手压桌面使桌面发生了形变。
(2)观察玻璃瓶的微小形变
在扁平玻璃瓶中装满水,瓶口用中间插有细玻璃管的软木塞塞紧,这时瓶内的水就会上升到细玻璃管中。如图所示,当用力挤压玻璃瓶的不同部位时,会发现细玻璃管中的水面会上升或下降。这说明玻璃瓶发生了形变。为了便于观察,可给水加色,并将细玻璃管固定在白色纸板上,纸板上可画细刻度线作为参考。
3.形变的种类:
①弹性形变:
某些发生形变的物体在撤去外力后能恢复原状,这种物体称为弹性体,对应的形变称为弹性形变,如波动的琴弦、拉开的弓箭。
②范性形变:
有些物体发生形变后不能恢复原状,这种形变称为范性形变,如压扁的面包、橡皮泥。
4.弹性限度:弹性体的形变不能无限增大,若超过一定的限度,撤去外力时物体就不能恢复原状,这个限度称为弹性限度。
弹簧被压缩,产生了形变,球被弹出去,说明有力的作用,这个力我们叫什么呢?
1.相互 的物体发生弹性形变时,由于物体要 ,物体会对与它接触的另一物体产生力的作用,这种力称为弹力。
2.通常所说的 、 、 等都是弹力。
接触
恢复原状
压力
支持力
拉力
二、弹 力
是不是所有的形变都能产生弹力呢?
3.弹力的产生条件:
①物体间相互接触
②物体间发生弹性形变
只有弹性形变产生的力才能叫做弹力。 因为只有撤去外力,物体为恢复到原来形状的而产生的力才叫作"弹力"
一铁块放在海绵上,铁块和海绵都发生了形变,从而在它们之间产生了弹力,如图所示。海绵对铁块的支持力是如何产生的?铁块对海绵的压力是怎样产生的?
铁块对海绵的压力是铁块发生了弹性形变,对与它接触的海绵产生力的作用(如图乙)。
海绵对铁块的支持力是海绵发生弹性形变,对与它接触的铁块产生力的作用(如图甲)。
(1)只有相互接触的物体间才可能有弹力。( )
(2)发生形变后的物体撤去外力后都能恢复原状。( )
(3)静止在水平地面上的物体受到向上的弹力是因为地面发生了形变。 ( )
(4)海绵受挤压会发生形变,桌面受挤压不会发生形变。( )
√
×
√
×
关于四种与足球有关的情境,下列说法正确的是( )
A.图甲,静止在草地上的足球对地面的压力就是它的重力
B.图乙,静止在水平地面上的两个足球间一定有弹力
C.图丙,踩在脚下且静止在地面上的足球一定只受一个弹力的作用
D.图丁,打到球网上的足球受到弹力是因为球网发生了形变
D
4.弹力的方向
(1)弹力方向 。
(2)几种常见弹力方向判断
绳子对物体拉力的方向总是沿着绳子而指向绳子收缩的方向
压力的方向总是垂直于接触面,指向被压的物体.
支持力的方向总是垂直支持面,指向被支持的物体.
FN
FT
FT1
FT2
F压
物块
桌面
小球
总是与物体形变的方向相反
(多选)关于弹力的方向,以下说法不正确的是( )
A.轻杆对物体的弹力方向总是沿着杆,并指向杆收缩的方向
B.轻绳对物体拉力的方向总是沿着绳,并指向绳收缩的方向
C.弹簧对物体的弹力方向,与弹簧形变的方向相同
D.物体受到的支持力的方向总是垂直于支持面,并指向被支持物体
AC
画出右面各物体所受弹力的示意图。
(1)图(a)中杆AB斜靠在半球体上静止,作出AB杆所受弹力的示意图。
(2)图(b)中用绳子将球挂在墙壁上,作出球所受弹力的示意图。
(3)图(c)中竖直悬挂在细绳上的光滑小球与斜面刚好接触而保持静止,作出小球所受弹力的示意图。
N1
N
N2
N1
N2
5.弹力有无的判断
条件法
拆除法
假设法
效果法
接触并发生形变
假设把与物体去掉,看能否维持原状
假设存在弹力,判断是否保持原状
有弹力,则该弹力必有相应的作用效果
(多选)在下列图中,a、b表面均光滑,且a、b均处于静止状态,天花板和地面均水平,A、D选项中细绳均竖直。a、b间一定有弹力的是( )
BC
第2节 科学探究:弹力 第2课时
第三章 相互作用
学习目标
1.能完成实验“探究弹簧弹力的大小与伸长量的关系”。
2.掌握胡克定律,并能用胡克定律进行简单的计算。
弹簧弹力的大小与形变量有什么关系呢?
提出问题
大胆猜想
弹簧弹力的大小与弹簧的形变量成正比
设计实验
实验:探究弹簧弹力的大小与伸长量的关系 胡克定律
1.实验目的
(1)探究弹簧弹力的大小与伸长量的关系。
(2)了解弹簧测力计的工作原理。
2.实验器材
铁架台、带挂钩的弹簧、钩码、
3.实验原理与设计
(1)将已知质量的钩码悬挂于弹簧上,由二力平衡可知,弹簧对钩码的弹力大小 钩码所受重力的大小。 F=G
(2)通过改变悬挂的钩码 来改变弹簧弹力的大小,测出弹簧未挂钩码时的 及挂钩码后的长度,可得出挂不同数量钩码情况下弹簧的 。
(3)由此可进一步得出弹簧弹力的大小与弹簧伸长量的关系。
等于
个数
长度(弹簧原长)
伸长量
4.实验步骤
(1)安装实验装置。
(2)用刻度尺测量弹簧原长。
(3)在弹簧挂钩上依次挂不同数量的钩码,并分别记下实验所挂钩码的总质量及弹簧长度。
次数 1 2 3 4 5
钩码质量m/g
弹簧弹力F/N
弹簧长度l/cm
弹簧伸长量x/cm
0
0
10.95
0
1.85
12.80
0.5
50
100
1.0
14.65
3.70
5.60
16.55
1.5
150
200
2.0
18.40
7.45
5.数据分析
(1)将数据及计算结果填入表中。
弹簧弹力的大小与伸长量的关系
(2)在坐标纸上作出弹簧弹力大小随伸长量变化的图像,并进行分析讨论。
弹簧弹力
F(N) 0 0.5 1.0 1.5 2.0
弹簧形变量x(cm) 0 1.85 3.70 5.60 7.45
F/N
x/cm
0
×
×
×
×
×
0.5
1.0
2.0
1.5
2.5
3.0
1
2
3
4
5
6
7
8
6.实验结论
(1)弹簧的弹力随伸长量的增大而 。
(2)在误差允许范围内,弹簧的弹力大小与 成正比。
增大
伸长量
用F表示
用x表示
(1)尽量选轻质弹簧以减小弹簧 带来的影响。
(2)实验中弹簧下端挂的钩码不要太多,避免 。
(3)测量长度时,应区别弹簧原长l0、实际长度l及形变量x三者之间的不同,明确三者之间的关系。为了减小弹簧自身重力带来的影响,测弹簧原长时应让弹簧在 时保持自由下垂状态,而不是平放在水平面上处于自然伸长状态。
7.注意事项
自身重力
超出弹簧的弹性限度
不挂钩码
(4)记录数据时要注意弹簧的弹力及形变量的对应关系及单位。
(5)描点作图时,应使尽量多的点落在画出的线上,可允许少数点均匀分布于线两侧,偏离太大的点应舍去,描出的线不应是折线,而应是平滑的曲线或直线。
在“探究弹簧弹力与形变量的关系”的实验中。
(1)下列实验步骤是甲同学准备完成的,请你帮他按正确操作的先后顺序,将各步骤前的字母写在横线上 。
A.以弹簧伸长量为横坐标,以弹力大小为纵坐标,描出各组数据(x,F)对应的点,并用平滑的曲线连接起来;
B.将铁架台固定于桌子上,并将弹簧的一端系于横梁上,在弹簧附近竖直固定一把刻度尺;
C.记下弹簧不挂钩码时,其下端对应的刻度l0;
D.依次在弹簧下端挂上1个、2个、3个、…、n个钩码,并分别记下钩码静止时,弹簧下端所对应的刻度并记录在表格内,然后取下钩码;
E.以弹簧伸长量为自变量,写出弹力的大小与弹簧伸长量的关系式;
F.解释函数表达式中常数的物理意义。
BCDAEF
(2)乙同学在做实验过程中,先把弹簧平放在桌面上使其自然伸长,用直尺测出弹簧的原长l0,再把弹簧竖直悬挂起来,挂上钩码后测出弹簧伸长后的长度L,把(L-l0)作为弹簧的伸长量x,由于弹簧自身重力的影响,这样操作最后画出的图线可能是____。
C
(3)如图是丙同学按正确步骤完成实验并画出弹簧弹力的大小和弹簧形变量的关系图线。写出该图线的函数表达式:____________。
F=0.43x(N)
如图所示,你能根据图像求出表达式F=kx中的比例系数k吗?它是什么物理量?
3.50
3.00
2.50
2.00
1.50
1.00
0.50
(0,0)
(13.6,3.5)
k为弹簧的劲度系数
胡克 英国科学家
(1635——1703)
胡克定律
1.内容:在弹性限度内,弹簧弹力F的大小
跟 成正比,即F= 。
2.劲度系数:式中的比例系数k称为弹簧的 ,单位是 ,符号是 ,是表示弹簧“软”“硬”程度的物理量。
3.劲度系数与弹性体的 、 等因素有关。
弹簧伸长(或压缩)的长度x
kx
劲度系数
N/m
形状
材料
牛顿每米
1.弹簧的形变量越大,弹力就会越大,若将弹簧拉得很长甚至拉直,还能用胡克定律计算吗?
不能。超出了弹簧的弹性限度,不能再用胡克定律计算了。
2.生活中说有的弹簧 “硬”,有的弹簧 “软”,指的就是它们的劲度系数不同。那弹簧的劲度系数跟哪些因素有关呢?
弹簧的劲度系数k只与弹簧本身有关,由弹簧本身的材料、长度、粗细、匝数等因素决定,它反应了弹簧的软硬程度,与弹力F的大小和形变量x无关。
例题:如图所示,一根轻弹簧长度由原来的5.00 cm伸长为6.00cm时,手受到的弹力为10.0N。那么,当这根弹簧伸长到6.20 cm时(在弹性限度内),手受到的弹力有多大?
C.弹簧的劲度系数k是由弹簧本身的性质决定的,与弹力F的大小和弹簧
形变量x的大小无关
D.弹簧的劲度系数在数值上等于弹簧伸长(或缩短)单位长度时弹力的数值
ACD
2.由实验测得某弹簧所受弹力F和弹簧的长度x的关系图像如图所示,求:
(1)该弹簧的原长;
答案 (1) 6 cm (2) 1 000 N/m
(2)该弹簧的劲度系数。
3.用如图甲所示的装置来探究胡克定律。轻质弹簧的左端与固定在墙上的拉力传感器连接,右端在水平拉力F的作用下从原长开始沿水平方向缓慢伸长,弹簧与水平面不接触,通过刻度尺可以读出弹簧的伸长量x,通过拉力传感器可以读出拉力F,多次测量F、x,作出F-x图像如图乙所示,回答下列问题:
(1)当弹力增大到一定程度时,图像变弯曲,原因什么?
弹簧形变量超出弹簧的弹性限度
(2)弹簧的劲度系数为____;
(3)弹簧的伸长量分别为x2和x1时,拉力传感器的示数之差为_________。
同课章节目录
- 绪论 撩开物理学的神秘面纱
- 一、源自然之问
- 二、探万物之秘
- 三、采科学之益
- 四、启智慧之迪
- 第1章 运动的描述
- 第1节 空间和时间
- 第2节 质点和位移
- 第3节 速度
- 第4节 加速度
- 第2章 匀变速直线运动
- 第1节 速度变化规律
- 第2节 位移变化规律
- 第3节 实验中的误差和有效数字
- 第4节 科学测量:做直线运动物体的瞬时速度
- 第5节 自由落体运动
- 第3章 相互作用
- 第1节 重力与重心
- 第2节 科学探究:弹力
- 第3节 摩擦力
- 第4章 力与平衡
- 第1节 科学探究:力的合成
- 第2节 力的分解
- 第3节 共点力的平衡
- 第5章 牛顿运动定律
- 第1节 牛顿第一运动定律
- 第2节 科学探究:加速度与力、质量的关系
- 第3节 牛顿第二运动定律
- 第4节 牛顿第三运动定律
- 第5节 超重与失重
