第三单元第1课时《倒数的认识(教材P27例1)》教学课件--人教版六年级上册
文档属性
| 名称 | 第三单元第1课时《倒数的认识(教材P27例1)》教学课件--人教版六年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 994.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 09:56:12 | ||
图片预览






文档简介
(共14张PPT)
倒数的认识
探究新知
基础练习
拓展练习
课堂小结
数学阅读
人教版数学六年级上册 第三单元
复习导入
口算下面各题。
×
3
8
8
3
=
1
×
7
15
15
7
=
1
5×
5
1
=
1
×12
12
1
=
1
1
×
6
13
13
6
=
1
×
2
9
9
2
=
复习导入
×
2
9
9
2
=
问题:1. 观察上面各题,你有什么发现?
2. 请你再写出几个这样的算式。
(一)观察前面的口算算式,揭示课题
1
×
7
15
15
7
=
1
5×
5
1
=
1
×12
12
1
=
1
1
×
6
13
13
6
=
1
×
3
8
8
3
=
探究新知
(两个数的乘积都是1。相乘的两个数的分子和分母正好颠倒了位置。)
(二)出示概念,加深理解
2. 请你举例说说,什么是“互为”倒数?
乘积是1的两个数互为倒数。 和 互为倒数,就是指:
的倒数是 , 的倒数是 。
3
8
8
3
8
3
3
8
3
8
8
3
探究新知
1.你能说说什么是互为倒数吗?能说 是倒数吗?为什么?
7
3
7
7
3
两个数的乘积为1,那么这两个数就互为倒数。不能说 是倒数,因为倒数是相对两个数的关系而言的, 只是一个分数, 和 才互为倒数, 是 的倒数, 是 的倒数。
7
3
3
7
7
3
7
3
3
7
3
7
7
3
(三)自学概念,探究理解
问题:1. 怎样找一个数的倒数呢?
下面哪两个数互为倒数?
5
3
6
2
7
3
5
6
1
1
7
2
0
探究新知
因为乘积是1的两个数互为倒数,所以只要两个数相乘,积是1,那么这两个数就一定互为倒数。
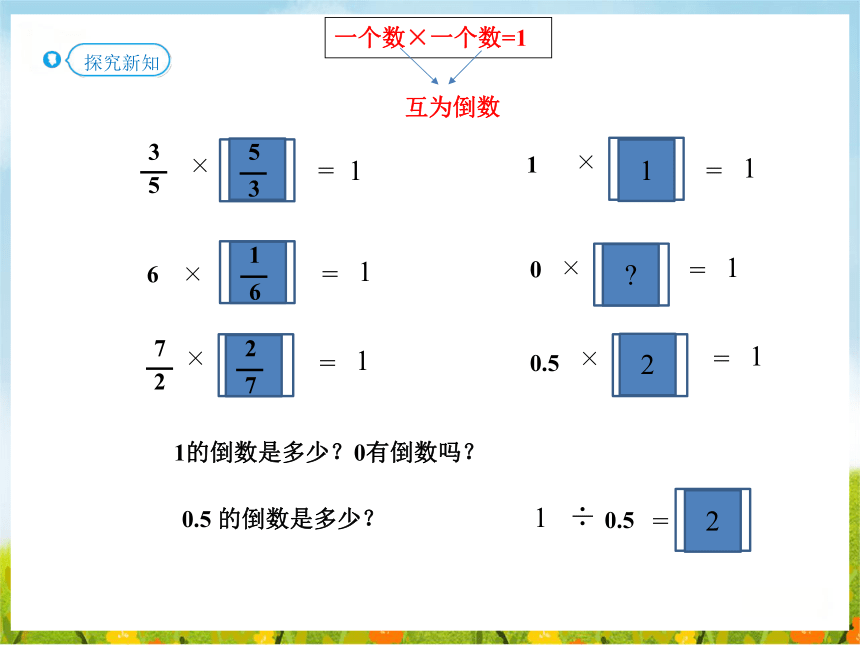
一个数×一个数=1
互为倒数
0.5
探究新知
1的倒数是多少?0有倒数吗?
一个数×一个数=1
互为倒数
5
3
×
=
1
6
×
=
1
1
×
=
1
2
7
=
1
×
0
×
=
1
0.5 的倒数是多少?
0.5
×
=
1
1
÷
=
0.5
3
5
6
1
7
2
1
2
2
探究新知
发现:
3. 因为1×1=1,所以1的倒数还是它本身。
4. 0与任何数相乘都不能等于1,所以0没有倒数。
5. 小数的倒数是用1除以这个小数。
问题:说说你是怎样写的?(反馈与交流)
写出下面各数的倒数。
9
16
11
4
35
8
7
15
4
探究新知
说说你的依据是什么?
1. 将互为倒数的两个数用线连起来。
7
6
3
13
13
3
8
1
8
6
7
26
25
100
100
1
59
99
99
59
25
26
基础练习
两个数相乘的积是1,这两个数互为倒数。
(1)0.8的倒数是( )或( )。
2. 写出下面各数的倒数。
1.25
4
5
(2) 的倒数是( )。
3
1
4
13
3
2. 找 的倒数,先要怎样做?
3
1
4
基础练习
5
4
(预设1: 0.8 ×1.25=1 预设2: 0.8= )
问题:1. 你是怎样想的?
先把 化成假分数,再写倒数。
3
1
4
(1) 与 的乘积为1,所以 和 互为倒数。( )
12
7
7
12
12
7
7
12
(4)一个数的倒数一定比这个数小。( )
(2) ,所以 、 、 互为倒数。( )
×
3
4
2
1
×
2
3
=1
2
1
3
4
2
3
(3)0的倒数还是0。( )
拓展练习
3. 下面的说法对不对?
√
×
×
×
问题:你认为谁说得对 说明你的理由。
4. 小兵和小丽谁说得对?
拓展练习
小兵说得对。乘积是1的两个数就互为倒数,这两个数可以是分数,也可以是小数或整数。
课堂小结
数学阅读
世界上最早期的分数,出现在埃及的阿默斯纸草卷。在阿默斯纸草卷中,我们见到了四千年前分数的一般记法,当时埃及人已经掌握了单分数——分子为1的分数的一般记法,并把单分数看作是整数的倒数。埃及人的这种认识以及对单分数的统计法,是十分了不起的,它告诉人们数不仅有整数,而且有它的倒数——单分数。
分数终究不只是单分数,大约在公元前5世纪,中国开始出现把两个整数相除的商看作分数的认识,这种认识正是现在的分数概念的基础。在这种认识下,一个除式也就表示一个分数,被除数放在除数的上面,最上面留放着商数,例如:若是假分数,化成带分数后与现在的记法不同的是,假分数的整数部分放在分数的上面,而不是放在左边。
大约在12世纪后期,在阿拉伯人的著作中,首先用一条短横线把分子、分母隔开来,这可以说是世界上最早的分数线;13世纪初,意大利数学家菲波那契在他的著作中介绍阿拉伯数字,也把分数的记法介绍到了欧洲。
西汉时期,张苍、耿寿昌等学者整理、删补自秦代以来的数学知识,编成了《九章算术》。在这本数学经典的《方田》章中,提出的完整的分数运算法则大约在15世纪才在欧洲流行。欧洲人普遍认为,这种算法起源于印度。实际上,印度在7世纪婆罗门笈多的著作中才开始有分数运算法则,这些法则都与《九章算术》中介绍的法则相同。而刘徽的《九章算术注》成书于魏景元四年(263年),所以,即使与刘徽的时代相比,印度也要比我们晚400年左右。
分数的起源
倒数的认识
探究新知
基础练习
拓展练习
课堂小结
数学阅读
人教版数学六年级上册 第三单元
复习导入
口算下面各题。
×
3
8
8
3
=
1
×
7
15
15
7
=
1
5×
5
1
=
1
×12
12
1
=
1
1
×
6
13
13
6
=
1
×
2
9
9
2
=
复习导入
×
2
9
9
2
=
问题:1. 观察上面各题,你有什么发现?
2. 请你再写出几个这样的算式。
(一)观察前面的口算算式,揭示课题
1
×
7
15
15
7
=
1
5×
5
1
=
1
×12
12
1
=
1
1
×
6
13
13
6
=
1
×
3
8
8
3
=
探究新知
(两个数的乘积都是1。相乘的两个数的分子和分母正好颠倒了位置。)
(二)出示概念,加深理解
2. 请你举例说说,什么是“互为”倒数?
乘积是1的两个数互为倒数。 和 互为倒数,就是指:
的倒数是 , 的倒数是 。
3
8
8
3
8
3
3
8
3
8
8
3
探究新知
1.你能说说什么是互为倒数吗?能说 是倒数吗?为什么?
7
3
7
7
3
两个数的乘积为1,那么这两个数就互为倒数。不能说 是倒数,因为倒数是相对两个数的关系而言的, 只是一个分数, 和 才互为倒数, 是 的倒数, 是 的倒数。
7
3
3
7
7
3
7
3
3
7
3
7
7
3
(三)自学概念,探究理解
问题:1. 怎样找一个数的倒数呢?
下面哪两个数互为倒数?
5
3
6
2
7
3
5
6
1
1
7
2
0
探究新知
因为乘积是1的两个数互为倒数,所以只要两个数相乘,积是1,那么这两个数就一定互为倒数。
一个数×一个数=1
互为倒数
0.5
探究新知
1的倒数是多少?0有倒数吗?
一个数×一个数=1
互为倒数
5
3
×
=
1
6
×
=
1
1
×
=
1
2
7
=
1
×
0
×
=
1
0.5 的倒数是多少?
0.5
×
=
1
1
÷
=
0.5
3
5
6
1
7
2
1
2
2
探究新知
发现:
3. 因为1×1=1,所以1的倒数还是它本身。
4. 0与任何数相乘都不能等于1,所以0没有倒数。
5. 小数的倒数是用1除以这个小数。
问题:说说你是怎样写的?(反馈与交流)
写出下面各数的倒数。
9
16
11
4
35
8
7
15
4
探究新知
说说你的依据是什么?
1. 将互为倒数的两个数用线连起来。
7
6
3
13
13
3
8
1
8
6
7
26
25
100
100
1
59
99
99
59
25
26
基础练习
两个数相乘的积是1,这两个数互为倒数。
(1)0.8的倒数是( )或( )。
2. 写出下面各数的倒数。
1.25
4
5
(2) 的倒数是( )。
3
1
4
13
3
2. 找 的倒数,先要怎样做?
3
1
4
基础练习
5
4
(预设1: 0.8 ×1.25=1 预设2: 0.8= )
问题:1. 你是怎样想的?
先把 化成假分数,再写倒数。
3
1
4
(1) 与 的乘积为1,所以 和 互为倒数。( )
12
7
7
12
12
7
7
12
(4)一个数的倒数一定比这个数小。( )
(2) ,所以 、 、 互为倒数。( )
×
3
4
2
1
×
2
3
=1
2
1
3
4
2
3
(3)0的倒数还是0。( )
拓展练习
3. 下面的说法对不对?
√
×
×
×
问题:你认为谁说得对 说明你的理由。
4. 小兵和小丽谁说得对?
拓展练习
小兵说得对。乘积是1的两个数就互为倒数,这两个数可以是分数,也可以是小数或整数。
课堂小结
数学阅读
世界上最早期的分数,出现在埃及的阿默斯纸草卷。在阿默斯纸草卷中,我们见到了四千年前分数的一般记法,当时埃及人已经掌握了单分数——分子为1的分数的一般记法,并把单分数看作是整数的倒数。埃及人的这种认识以及对单分数的统计法,是十分了不起的,它告诉人们数不仅有整数,而且有它的倒数——单分数。
分数终究不只是单分数,大约在公元前5世纪,中国开始出现把两个整数相除的商看作分数的认识,这种认识正是现在的分数概念的基础。在这种认识下,一个除式也就表示一个分数,被除数放在除数的上面,最上面留放着商数,例如:若是假分数,化成带分数后与现在的记法不同的是,假分数的整数部分放在分数的上面,而不是放在左边。
大约在12世纪后期,在阿拉伯人的著作中,首先用一条短横线把分子、分母隔开来,这可以说是世界上最早的分数线;13世纪初,意大利数学家菲波那契在他的著作中介绍阿拉伯数字,也把分数的记法介绍到了欧洲。
西汉时期,张苍、耿寿昌等学者整理、删补自秦代以来的数学知识,编成了《九章算术》。在这本数学经典的《方田》章中,提出的完整的分数运算法则大约在15世纪才在欧洲流行。欧洲人普遍认为,这种算法起源于印度。实际上,印度在7世纪婆罗门笈多的著作中才开始有分数运算法则,这些法则都与《九章算术》中介绍的法则相同。而刘徽的《九章算术注》成书于魏景元四年(263年),所以,即使与刘徽的时代相比,印度也要比我们晚400年左右。
分数的起源
