第三单元第7课时《分数除法的应用( 三)(P40例6)》教学课件--人教版六年级上册
文档属性
| 名称 | 第三单元第7课时《分数除法的应用( 三)(P40例6)》教学课件--人教版六年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
分数除法的应用( 三)
探究新知
基础练习
拓展练习
课堂小结
数学阅读
人教版数学六年级上册 第三单元
复习导入
看图回答问题:
①从图中你知道了什么?
女生人数
男生人数
②根据线段图,你能说说男、女生人数间的数量关系吗?
复习导入
看图回答问题:
女生人数
男生人数
③如果男生有x人,女生有多少人?你是怎样得到的?
复习导入
④如果女生有x人,男生有多少人?你是怎样得到的?
女生
男生
1
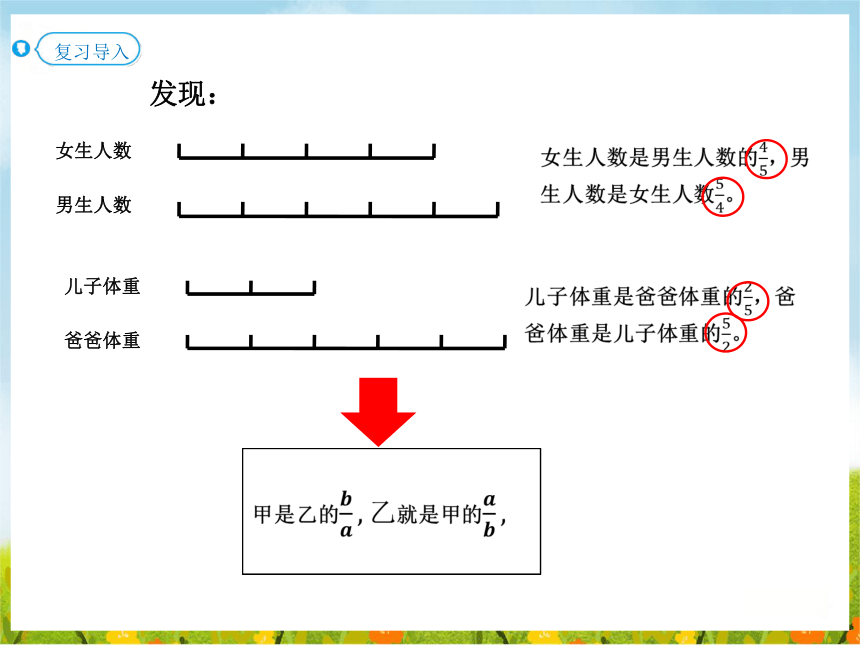
发现:
女生人数
男生人数
复习导入
儿子体重
爸爸体重
(一)阅读与理解
①从题目中你知道了什么?
③这道题怎样解答,请你根据题意画出线段图。
②怎样理解“下半场得分是上半场的一半”这句话?
探究新知
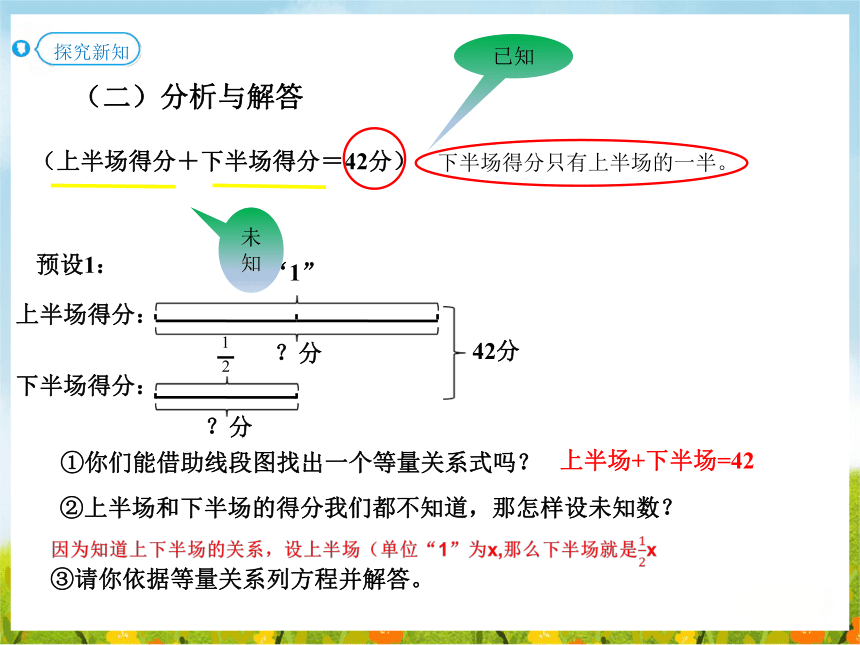
(二)分析与解答
①你们能借助线段图找出一个等量关系式吗?
②上半场和下半场的得分我们都不知道,那怎样设未知数?
(上半场得分+下半场得分=42分)
③请你依据等量关系列方程并解答。
上半场得分:
下半场得分:
“1”
?分
?分
2
1
42分
预设1:
探究新知
已知
未知
下半场得分只有上半场的一半。
上半场+下半场=42
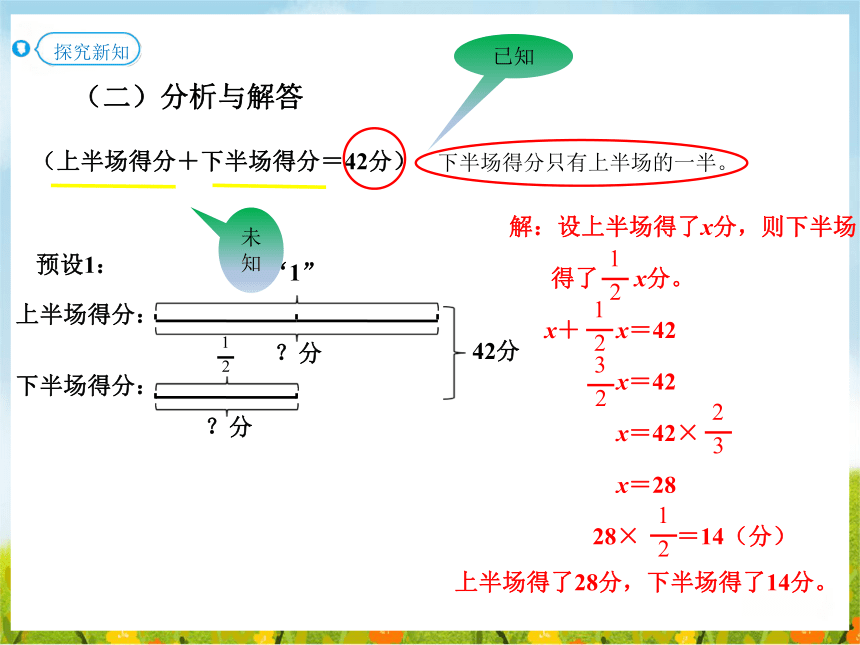
(二)分析与解答
(上半场得分+下半场得分=42分)
上半场得分:
下半场得分:
“1”
?分
?分
2
1
42分
预设1:
解:设上半场得了x分,则下半场
得了 x分。
x+ x=42
x=42
x=42×
x=28
28× =14(分)
2
1
2
1
2
3
3
2
2
1
探究新知
已知
未知
下半场得分只有上半场的一半。
上半场得了28分,下半场得了14分。
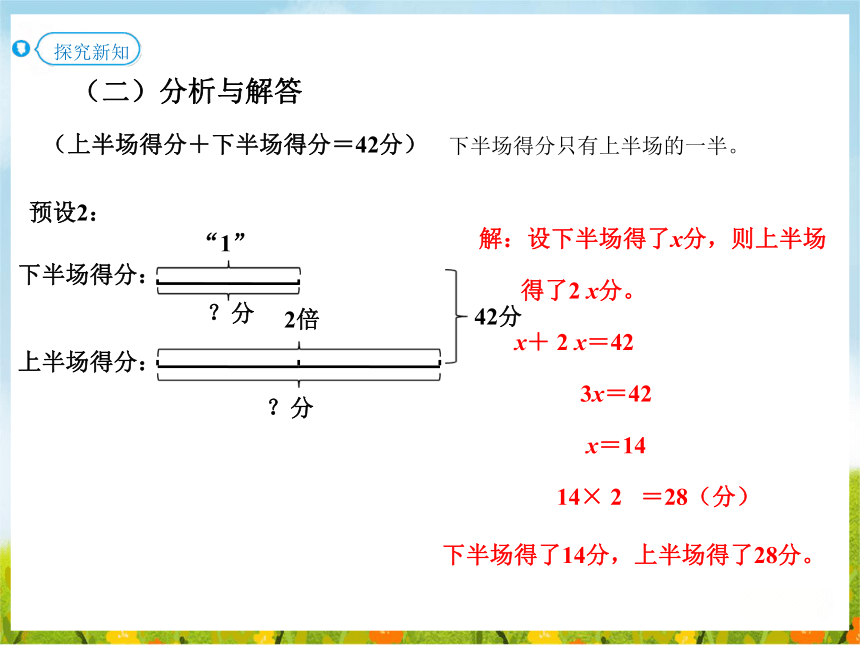
(二)分析与解答
①如果把下半场得分看作单位“1”,那么上半场得分是下半场的几倍?
②应该怎样设未知数?说说你列的方程。
预设2:
“1”
上半场得分:
下半场得分:
42分
?分
?分
2倍
探究新知
(上半场得分+下半场得分=42分)
下半场得分只有上半场的一半。
如果把下半场看成单位“1”,则上半场是下半场的2倍。
设下半场为x分,则上半场就是2x分。
(二)分析与解答
预设2:
“1”
上半场得分:
下半场得分:
42分
?分
?分
2倍
探究新知
(上半场得分+下半场得分=42分)
下半场得分只有上半场的一半。
解:设下半场得了x分,则上半场
得了2 x分。
x+ 2 x=42
3x=42
x=14
14× 2 =28(分)
下半场得了14分,上半场得了28分。
观察这两个方程,说一说在两个方程里,分别把谁看成单位”1”
解:设上半场得了x分,则下半场
得了 x分。
x+ x=42
x=42
x=42×
x=28
28× =14(分)
2
1
2
1
2
3
3
2
2
1
解:设下半场得了x分,则上半场
得了2x分。
x+2x=42
3x=42
x=42 ÷3
x=14
14× 2 =28(分)
探究新知
发现:
把上半场看成单位1
把下半场看成单位1
(三)回顾与反思
刚才同学们列出了两个不同的方程,分别求出了上、下半场的得分,那么对不对呢?可以怎样检验?
方法1:
看看上、下半场的得分和是不是42分
方法2:
看看下半场得分是不是上半场的
2
1
探究新知
28 +14 =42(分)
√
√
探究新知
(四)用算术方法解决和倍问题
什么是和倍问题?
已知两个数的和,同时知道一个数是另一个数的几分之几(或者知道一个数是另一数的几倍)
例如:
“1”
上半场得分:
下半场得分:
42分
?分
?分
2倍
如果把下半场得分看成单位1,上半场就是2倍的单位1,从图上可以看出一共是3个单位1,它们的量的和是42,那么单位1的量就是42÷3=14,即下半场的得分是14分,那么上半场得分就是:14×2=28(分)。
探究新知
(四)用算术方法解决和倍问题
什么是和倍问题?
已知两个数的和,同时知道一个数是另一个数的几分之几(或者知道一个数是另一数的几倍)
例如:
上半场得分:
下半场得分:
“1”
?分
?分
2
1
42分
探究新知
上面例题中,没有用方程,而是用算术的方法去解决,你能总结一下用算术方法解决和倍问题的方法吗?
用算术方法解决和倍问题,关系是找出单位“1”的总份数,然后用总量除以单位“1”的总份数,就能得到单位“1” 的量。
如在上面的例题中,如果把下半场看成单位“1”,那么上半场就相当于2个单位“1”,一共就是3个单位“1”,用总量42除以单位量的总份数,即42÷3=14,那么这个14就是单位“1”的量,即下半场的得分。
如果把上半场看成单位“1”,那么下半场就相当于个单位“1”,一共就是个单位“1”,用总量42除以单位量的总份数,即42÷ =28,那么这个28就是单位“1”的量,即上半场的得分。
探究新知
120-45=75(本)
小明的书
小华的书
“1”
小华的书:
小明的书:
120本
?本
?本
倍
探究新知
120-75=45(本)
“1”
小华的书:
小明的书:
120本
?本
?本
小华的书
小明的书
探究新知
120÷(1+ )=120÷ =120× =45(本)
把小明的书看成单位“1”,求小明的书:
120÷(1+ )=120÷ =120× =75(本)
把小华的书看成单位“1”,求小华的书:
观察这两个算式,你发现了什么?
都是用总量乘了一个分数,而且这两个分数 的分母相同,分子相加等于分母
这个分数是怎么来的,你知道吗?
1+ =
1+ =
都是根据它们两个之间的关系推理出来的。
探究新知
“1”
小华的书:
小明的书:
120本
?本
?本
120本是谁对应的量?
两个人对应的量
用图示法,你能表示两个的总量吗?
这是谁的书?
这是谁的书?
现在一共是多少份?
3+5=8
如果把这总量看成单位“1”,那么小明占几分之几 小华占几分之几?
你现在看明白这个分数是怎么得来的吗?
和倍问题小技巧
探究新知
通过刚才的观察,你能总结一下和倍问题的算术解法吗
知道两个数的和,并且知道两个数之间的倍数或者分数关系,比如甲是乙的显然是较小的数,那么它就占总份数的,乙是较大的数,那么它就占总份数的,我们用总量分别乘它们占总量的分率,就可以得出它们对应的量。
六年级一共40名学生,男生是女生的,男女生各有多少人?
1+3=4 男生占总量的 女生占总量的
提示:这种解题方法需要我们在解题前进行推理,需要把推理的过程全部写进去,别人才能理解,所以,这种方法一般只适合填空、选择或者判断,如果是应用题,我们一般都用方程解决。
108万台
“1”
下半年产量:
上半年产量:
?万台
?万台
上半年产量+下半年产量=全年产量
2.把下半年产量看成单位1,画出线段图。
某电视厂去年全年生产电视机108万台,其中上
半年产量是下半年的 。这个电视机厂去年上
半年和下半年的产量分别是多少万台?
5
4
解:设下半年生产x万台,则上
半年生产 x万台。
x+ x=108
x=108
x=60
60 × =48(万台)
5
4
5
4
5
9
5
4
基础练习
1.找等量关系式:
3.根据等量关系列方程。
如果把上半年的产量看作是单位“1”,那么下半年的产量是上半年的几分之几?应该怎样设未知数?
上半年产量+下半年产量=全年产量
2.把上半年产量看成单位1,画出线段图。
108万台
“1”
下半年产量:
上半年产量:
?万台
?万台
某电视厂去年全年生产电视机108万台,其中上
半年产量是下半年的 。这个电视机厂去年上
半年和下半年的产量分别是多少万台?
5
4
解:设上半年生产x万台,则下半
年生产 x万台。
x+ x=108
x=108
x=48
108-48=60(万台)
4
5
4
5
4
9
基础练习
1.找数量关系式:
3.根据等量关系列方程。
上衣价钱:
裤子价钱:
“1”
?元
?元
300元
预设1:
解:设上衣的价钱为x元,则裤
子的价钱为 x元。
x+ x=300
x=300
x=180
180 × =120(元)
3
2
3
2
3
5
3
2
拓展练习
上衣价钱:
裤子价钱:
“1”
?元
?元
300元
如果把裤子的价钱看作是单位“1”,那么上衣的价钱是裤子的几分之几?应该怎样设未知数?
问题:
预设2:
解:设裤子的价钱为x元,则上
衣的价钱为 x元。
x+ x=300
x=300
x=120
300-120=180(元)
2
3
2
3
2
5
拓展练习
课堂小结
数学阅读
清晨,甲、乙、丙、丁四个小朋友走进森林采蘑菇。九时的时候,他们准备往回走。走出森林之前,各人数了数篮子里的蘑菇,四个人加起来总共有72朵。但甲采的蘑菇有一半能吃。在往回走的路上,甲把有毒的蘑菇全都丢了;乙的篮子底坏了,漏下两朵,被丙拾起来放在篮子里。这时,他们三个人的蘑菇数正好相等。而丁呢,他在出森林的路上又采了一些,使篮子里的蘑菇增加了一倍。到走出森林后,他们坐下来,又每人各自数了数篮子里的蘑菇。这次,大家的数目都相等。你算算看,他们准备往回走出森林时,各人篮子里有多少蘑菇 走出森林后,又有多少蘑菇 聪明的你知道吗
采蘑菇的故事
分数除法的应用( 三)
探究新知
基础练习
拓展练习
课堂小结
数学阅读
人教版数学六年级上册 第三单元
复习导入
看图回答问题:
①从图中你知道了什么?
女生人数
男生人数
②根据线段图,你能说说男、女生人数间的数量关系吗?
复习导入
看图回答问题:
女生人数
男生人数
③如果男生有x人,女生有多少人?你是怎样得到的?
复习导入
④如果女生有x人,男生有多少人?你是怎样得到的?
女生
男生
1
发现:
女生人数
男生人数
复习导入
儿子体重
爸爸体重
(一)阅读与理解
①从题目中你知道了什么?
③这道题怎样解答,请你根据题意画出线段图。
②怎样理解“下半场得分是上半场的一半”这句话?
探究新知
(二)分析与解答
①你们能借助线段图找出一个等量关系式吗?
②上半场和下半场的得分我们都不知道,那怎样设未知数?
(上半场得分+下半场得分=42分)
③请你依据等量关系列方程并解答。
上半场得分:
下半场得分:
“1”
?分
?分
2
1
42分
预设1:
探究新知
已知
未知
下半场得分只有上半场的一半。
上半场+下半场=42
(二)分析与解答
(上半场得分+下半场得分=42分)
上半场得分:
下半场得分:
“1”
?分
?分
2
1
42分
预设1:
解:设上半场得了x分,则下半场
得了 x分。
x+ x=42
x=42
x=42×
x=28
28× =14(分)
2
1
2
1
2
3
3
2
2
1
探究新知
已知
未知
下半场得分只有上半场的一半。
上半场得了28分,下半场得了14分。
(二)分析与解答
①如果把下半场得分看作单位“1”,那么上半场得分是下半场的几倍?
②应该怎样设未知数?说说你列的方程。
预设2:
“1”
上半场得分:
下半场得分:
42分
?分
?分
2倍
探究新知
(上半场得分+下半场得分=42分)
下半场得分只有上半场的一半。
如果把下半场看成单位“1”,则上半场是下半场的2倍。
设下半场为x分,则上半场就是2x分。
(二)分析与解答
预设2:
“1”
上半场得分:
下半场得分:
42分
?分
?分
2倍
探究新知
(上半场得分+下半场得分=42分)
下半场得分只有上半场的一半。
解:设下半场得了x分,则上半场
得了2 x分。
x+ 2 x=42
3x=42
x=14
14× 2 =28(分)
下半场得了14分,上半场得了28分。
观察这两个方程,说一说在两个方程里,分别把谁看成单位”1”
解:设上半场得了x分,则下半场
得了 x分。
x+ x=42
x=42
x=42×
x=28
28× =14(分)
2
1
2
1
2
3
3
2
2
1
解:设下半场得了x分,则上半场
得了2x分。
x+2x=42
3x=42
x=42 ÷3
x=14
14× 2 =28(分)
探究新知
发现:
把上半场看成单位1
把下半场看成单位1
(三)回顾与反思
刚才同学们列出了两个不同的方程,分别求出了上、下半场的得分,那么对不对呢?可以怎样检验?
方法1:
看看上、下半场的得分和是不是42分
方法2:
看看下半场得分是不是上半场的
2
1
探究新知
28 +14 =42(分)
√
√
探究新知
(四)用算术方法解决和倍问题
什么是和倍问题?
已知两个数的和,同时知道一个数是另一个数的几分之几(或者知道一个数是另一数的几倍)
例如:
“1”
上半场得分:
下半场得分:
42分
?分
?分
2倍
如果把下半场得分看成单位1,上半场就是2倍的单位1,从图上可以看出一共是3个单位1,它们的量的和是42,那么单位1的量就是42÷3=14,即下半场的得分是14分,那么上半场得分就是:14×2=28(分)。
探究新知
(四)用算术方法解决和倍问题
什么是和倍问题?
已知两个数的和,同时知道一个数是另一个数的几分之几(或者知道一个数是另一数的几倍)
例如:
上半场得分:
下半场得分:
“1”
?分
?分
2
1
42分
探究新知
上面例题中,没有用方程,而是用算术的方法去解决,你能总结一下用算术方法解决和倍问题的方法吗?
用算术方法解决和倍问题,关系是找出单位“1”的总份数,然后用总量除以单位“1”的总份数,就能得到单位“1” 的量。
如在上面的例题中,如果把下半场看成单位“1”,那么上半场就相当于2个单位“1”,一共就是3个单位“1”,用总量42除以单位量的总份数,即42÷3=14,那么这个14就是单位“1”的量,即下半场的得分。
如果把上半场看成单位“1”,那么下半场就相当于个单位“1”,一共就是个单位“1”,用总量42除以单位量的总份数,即42÷ =28,那么这个28就是单位“1”的量,即上半场的得分。
探究新知
120-45=75(本)
小明的书
小华的书
“1”
小华的书:
小明的书:
120本
?本
?本
倍
探究新知
120-75=45(本)
“1”
小华的书:
小明的书:
120本
?本
?本
小华的书
小明的书
探究新知
120÷(1+ )=120÷ =120× =45(本)
把小明的书看成单位“1”,求小明的书:
120÷(1+ )=120÷ =120× =75(本)
把小华的书看成单位“1”,求小华的书:
观察这两个算式,你发现了什么?
都是用总量乘了一个分数,而且这两个分数 的分母相同,分子相加等于分母
这个分数是怎么来的,你知道吗?
1+ =
1+ =
都是根据它们两个之间的关系推理出来的。
探究新知
“1”
小华的书:
小明的书:
120本
?本
?本
120本是谁对应的量?
两个人对应的量
用图示法,你能表示两个的总量吗?
这是谁的书?
这是谁的书?
现在一共是多少份?
3+5=8
如果把这总量看成单位“1”,那么小明占几分之几 小华占几分之几?
你现在看明白这个分数是怎么得来的吗?
和倍问题小技巧
探究新知
通过刚才的观察,你能总结一下和倍问题的算术解法吗
知道两个数的和,并且知道两个数之间的倍数或者分数关系,比如甲是乙的显然是较小的数,那么它就占总份数的,乙是较大的数,那么它就占总份数的,我们用总量分别乘它们占总量的分率,就可以得出它们对应的量。
六年级一共40名学生,男生是女生的,男女生各有多少人?
1+3=4 男生占总量的 女生占总量的
提示:这种解题方法需要我们在解题前进行推理,需要把推理的过程全部写进去,别人才能理解,所以,这种方法一般只适合填空、选择或者判断,如果是应用题,我们一般都用方程解决。
108万台
“1”
下半年产量:
上半年产量:
?万台
?万台
上半年产量+下半年产量=全年产量
2.把下半年产量看成单位1,画出线段图。
某电视厂去年全年生产电视机108万台,其中上
半年产量是下半年的 。这个电视机厂去年上
半年和下半年的产量分别是多少万台?
5
4
解:设下半年生产x万台,则上
半年生产 x万台。
x+ x=108
x=108
x=60
60 × =48(万台)
5
4
5
4
5
9
5
4
基础练习
1.找等量关系式:
3.根据等量关系列方程。
如果把上半年的产量看作是单位“1”,那么下半年的产量是上半年的几分之几?应该怎样设未知数?
上半年产量+下半年产量=全年产量
2.把上半年产量看成单位1,画出线段图。
108万台
“1”
下半年产量:
上半年产量:
?万台
?万台
某电视厂去年全年生产电视机108万台,其中上
半年产量是下半年的 。这个电视机厂去年上
半年和下半年的产量分别是多少万台?
5
4
解:设上半年生产x万台,则下半
年生产 x万台。
x+ x=108
x=108
x=48
108-48=60(万台)
4
5
4
5
4
9
基础练习
1.找数量关系式:
3.根据等量关系列方程。
上衣价钱:
裤子价钱:
“1”
?元
?元
300元
预设1:
解:设上衣的价钱为x元,则裤
子的价钱为 x元。
x+ x=300
x=300
x=180
180 × =120(元)
3
2
3
2
3
5
3
2
拓展练习
上衣价钱:
裤子价钱:
“1”
?元
?元
300元
如果把裤子的价钱看作是单位“1”,那么上衣的价钱是裤子的几分之几?应该怎样设未知数?
问题:
预设2:
解:设裤子的价钱为x元,则上
衣的价钱为 x元。
x+ x=300
x=300
x=120
300-120=180(元)
2
3
2
3
2
5
拓展练习
课堂小结
数学阅读
清晨,甲、乙、丙、丁四个小朋友走进森林采蘑菇。九时的时候,他们准备往回走。走出森林之前,各人数了数篮子里的蘑菇,四个人加起来总共有72朵。但甲采的蘑菇有一半能吃。在往回走的路上,甲把有毒的蘑菇全都丢了;乙的篮子底坏了,漏下两朵,被丙拾起来放在篮子里。这时,他们三个人的蘑菇数正好相等。而丁呢,他在出森林的路上又采了一些,使篮子里的蘑菇增加了一倍。到走出森林后,他们坐下来,又每人各自数了数篮子里的蘑菇。这次,大家的数目都相等。你算算看,他们准备往回走出森林时,各人篮子里有多少蘑菇 走出森林后,又有多少蘑菇 聪明的你知道吗
采蘑菇的故事
