第五单元第4课时《圆的面积》教学课件--人教版六年级上册
文档属性
| 名称 | 第五单元第4课时《圆的面积》教学课件--人教版六年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 09:56:12 | ||
图片预览




文档简介
(共14张PPT)
圆的面积
探究新知
基础练习
拓展练习
课堂小结
数学阅读
人教版数学六年级上册 第五单元
复习导入
一、判断。
直径都是半径的2倍。 ( )
同一个圆中,半径都相等。 ( )
在连接圆上任意两点的线段中,直径最长。 ( )
画一个直径是4厘米的圆,圆规两脚应叉开4厘米。 ( )
5.水桶是圆形的。( )
6.所有的直径都相等。( )
7.圆的直径是半径的2倍。( )
8.两个圆的直径相等,它们的半径也一定相等。( )
复习导入
×
√
√
×
×
×
×
√
二、填空。
1.一个圆中最长的线段是6厘米,这个圆的周长是( )厘米。
2.一个圆的半径扩大到原来的2倍,周长扩大到原来( )倍。
3.一只大挂钟的时针长60厘米,一天内这只大挂钟时针尖端经过路程的总长是( ) 米。
4.把一个圆分割成两个相等的半圆后,它的周长增加了6厘米,原来这个圆的半径是( )厘米。
5.在一个长10厘米,宽5厘米的长方形里,画一个最大的圆,这个圆的半径是( )分米。
复习导入
2
9.0432
1.5
0.25
18.84
一、问题引入
探究新知
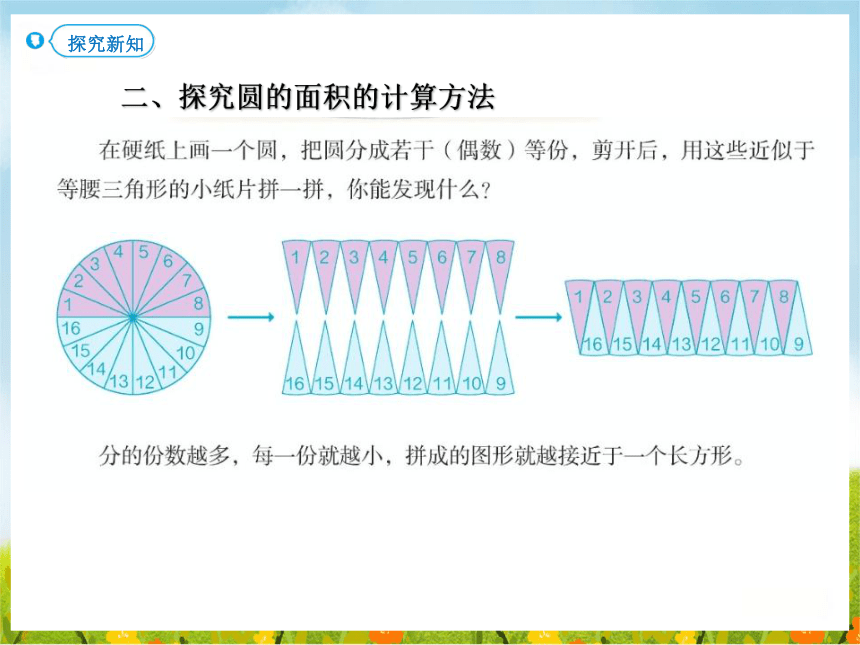
二、探究圆的面积的计算方法
探究新知
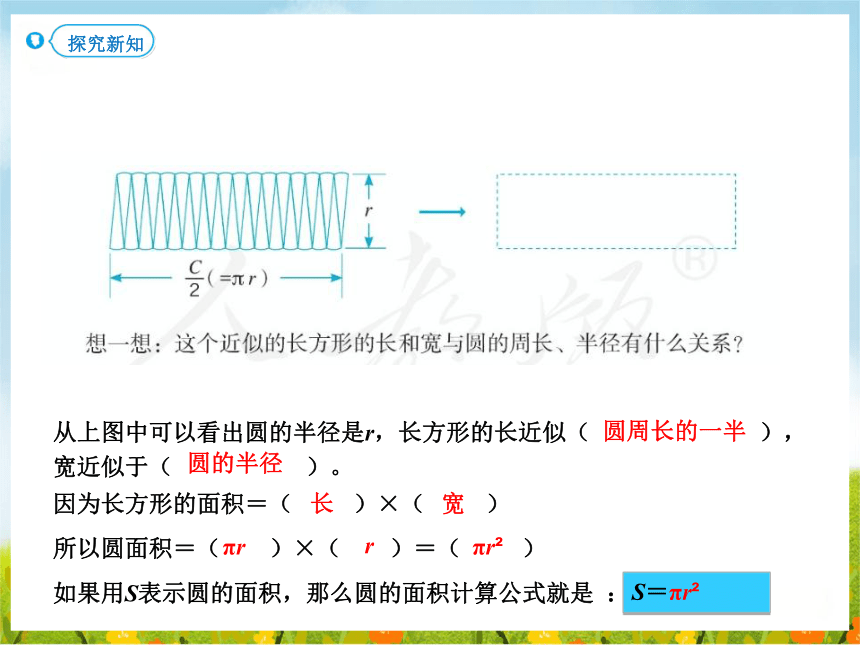
从上图中可以看出圆的半径是r,长方形的长近似( ),宽近似于( )。
因为长方形的面积=( )×( )
所以圆面积=( )×( )=( )
如果用S表示圆的面积,那么圆的面积计算公式就是 :
圆周长的一半
圆的半径
长
宽
πr
r
πr
S=πr
探究新知
圆形草坪的直径是20 m,每平方米草皮8元,铺满这个草坪需要多少钱?
20÷2=10(m)
314×8=2512(元)
3.14×10 =314(m )
答:铺满草皮需要2512元。
三、应用公式
探究新知
1.一个圆形桌面的直径是1m,它的面积是多少平方米?
1÷2=0.5(m)
3.14×0.5 =0.785(m )
答:它的面积是0.785m 。
基础练习
2.填空题。
1.把一个圆分成32等份,然后剪开拼成一个近似的长方形。这个长方形的长相当于( ),长方形的宽就是圆的
( )。因为长方形的面积是( ),所以圆的面积是( )。
2.一个圆的半径是6厘米,它的周长是( ),面积是
( )。
3.一个圆的周长是25.12分米,它的面积是( )。
基础练习
周长的一半(πr)
半径
长×宽(πr×r)
π
18.84厘米
113.03平方厘米
50.24平方分米
1.一个圆形花园的直径是16米,其中八分之三的面积种了玫瑰。种玫瑰的面积有多大?
拓展练习
3.14×米)
花园面积:
种玫瑰的面积:
拓展练习
O
2.图中正方形的面积是16平方厘米,那么圆的面积是多少平方厘米?
从正方形面积是16平方厘米,可以算出正方形边长为4厘米。正方形边长即为圆的半径。
答:圆的面积是50.24平方厘米。
课堂小结
数学阅读
面积概念的形成和人们对圆面积的探究
面积的概念很早就形成了。在古代埃及,尼罗河每年泛滥一次,洪水给两岸带来了肥沃的淤泥,但也抹掉了田地之间的界限标志。水退了,人们要重新划出田地的界限,就必须丈量和计算田地,于是逐渐有了面积的概念。
在数学上是这样来研究面积问题的:首先规定边长为1的正方形的面积为1,并将其作为不证自明的公理。然后用这样的所谓单位正方形来度量其他平面几何图形。较为简单的正方形和长方形的面积是很容易得到的,利用割补法可以把平行四边形的面积问题转化为长方形的面积问题,进而又可以得到三角形的面积。于是多边形的面积就可以转化为若干三角形的面积。
关于圆的面积的探究,古代数学家都做过很大的贡献:
我国古代的数学家祖冲之,从圆内接正六边形入手,让边数成倍增加,用圆内接正多边形的面积去逼近圆面积。
古希腊的数学家,从圆内接正多边形和外切正多边形同时入手,不断增加它们的边数,从里外两个方面去逼近圆面积。
古印度的数学家,采用类似切西瓜的办法,把圆切成许多小瓣,再把这些小瓣对接成一个长方形,用长方形的面积去代替圆面积。
众多的古代数学家煞费苦心,巧妙构思,为求圆面积作出了十分宝贵的贡献。为后人解决这个问题开辟了道路。
开普勒的求解方法
16世纪的德国天文学家开普勒,当过数学老师,他对求面积的问题非常感兴趣,曾进行过深入的研究。他想,古代数学家用分割的方法去求圆面积,所得到的结果都是近似值。为了提高近似程度,他们不断地增加分割的次数。但是,不管分割多少次,几千几万次,只要是有限次,所求出来的总是圆面积的近似值。要想求出圆面积的精确值,必须分割无穷多次,把圆分成无穷多等分才行。
圆的面积
探究新知
基础练习
拓展练习
课堂小结
数学阅读
人教版数学六年级上册 第五单元
复习导入
一、判断。
直径都是半径的2倍。 ( )
同一个圆中,半径都相等。 ( )
在连接圆上任意两点的线段中,直径最长。 ( )
画一个直径是4厘米的圆,圆规两脚应叉开4厘米。 ( )
5.水桶是圆形的。( )
6.所有的直径都相等。( )
7.圆的直径是半径的2倍。( )
8.两个圆的直径相等,它们的半径也一定相等。( )
复习导入
×
√
√
×
×
×
×
√
二、填空。
1.一个圆中最长的线段是6厘米,这个圆的周长是( )厘米。
2.一个圆的半径扩大到原来的2倍,周长扩大到原来( )倍。
3.一只大挂钟的时针长60厘米,一天内这只大挂钟时针尖端经过路程的总长是( ) 米。
4.把一个圆分割成两个相等的半圆后,它的周长增加了6厘米,原来这个圆的半径是( )厘米。
5.在一个长10厘米,宽5厘米的长方形里,画一个最大的圆,这个圆的半径是( )分米。
复习导入
2
9.0432
1.5
0.25
18.84
一、问题引入
探究新知
二、探究圆的面积的计算方法
探究新知
从上图中可以看出圆的半径是r,长方形的长近似( ),宽近似于( )。
因为长方形的面积=( )×( )
所以圆面积=( )×( )=( )
如果用S表示圆的面积,那么圆的面积计算公式就是 :
圆周长的一半
圆的半径
长
宽
πr
r
πr
S=πr
探究新知
圆形草坪的直径是20 m,每平方米草皮8元,铺满这个草坪需要多少钱?
20÷2=10(m)
314×8=2512(元)
3.14×10 =314(m )
答:铺满草皮需要2512元。
三、应用公式
探究新知
1.一个圆形桌面的直径是1m,它的面积是多少平方米?
1÷2=0.5(m)
3.14×0.5 =0.785(m )
答:它的面积是0.785m 。
基础练习
2.填空题。
1.把一个圆分成32等份,然后剪开拼成一个近似的长方形。这个长方形的长相当于( ),长方形的宽就是圆的
( )。因为长方形的面积是( ),所以圆的面积是( )。
2.一个圆的半径是6厘米,它的周长是( ),面积是
( )。
3.一个圆的周长是25.12分米,它的面积是( )。
基础练习
周长的一半(πr)
半径
长×宽(πr×r)
π
18.84厘米
113.03平方厘米
50.24平方分米
1.一个圆形花园的直径是16米,其中八分之三的面积种了玫瑰。种玫瑰的面积有多大?
拓展练习
3.14×米)
花园面积:
种玫瑰的面积:
拓展练习
O
2.图中正方形的面积是16平方厘米,那么圆的面积是多少平方厘米?
从正方形面积是16平方厘米,可以算出正方形边长为4厘米。正方形边长即为圆的半径。
答:圆的面积是50.24平方厘米。
课堂小结
数学阅读
面积概念的形成和人们对圆面积的探究
面积的概念很早就形成了。在古代埃及,尼罗河每年泛滥一次,洪水给两岸带来了肥沃的淤泥,但也抹掉了田地之间的界限标志。水退了,人们要重新划出田地的界限,就必须丈量和计算田地,于是逐渐有了面积的概念。
在数学上是这样来研究面积问题的:首先规定边长为1的正方形的面积为1,并将其作为不证自明的公理。然后用这样的所谓单位正方形来度量其他平面几何图形。较为简单的正方形和长方形的面积是很容易得到的,利用割补法可以把平行四边形的面积问题转化为长方形的面积问题,进而又可以得到三角形的面积。于是多边形的面积就可以转化为若干三角形的面积。
关于圆的面积的探究,古代数学家都做过很大的贡献:
我国古代的数学家祖冲之,从圆内接正六边形入手,让边数成倍增加,用圆内接正多边形的面积去逼近圆面积。
古希腊的数学家,从圆内接正多边形和外切正多边形同时入手,不断增加它们的边数,从里外两个方面去逼近圆面积。
古印度的数学家,采用类似切西瓜的办法,把圆切成许多小瓣,再把这些小瓣对接成一个长方形,用长方形的面积去代替圆面积。
众多的古代数学家煞费苦心,巧妙构思,为求圆面积作出了十分宝贵的贡献。为后人解决这个问题开辟了道路。
开普勒的求解方法
16世纪的德国天文学家开普勒,当过数学老师,他对求面积的问题非常感兴趣,曾进行过深入的研究。他想,古代数学家用分割的方法去求圆面积,所得到的结果都是近似值。为了提高近似程度,他们不断地增加分割的次数。但是,不管分割多少次,几千几万次,只要是有限次,所求出来的总是圆面积的近似值。要想求出圆面积的精确值,必须分割无穷多次,把圆分成无穷多等分才行。
