北师大版2025—2026学年八年级上册数学入学考试押题试卷(含答案)
文档属性
| 名称 | 北师大版2025—2026学年八年级上册数学入学考试押题试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 866.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 19:22:10 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
北师大版2025—2026学年八年级上册数学入学考试押题试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列计算正确的是( )
A. B.
C. D.
2.下列图案中不是轴对称图形的是( )
A.B.C. D.
3.下列事件中,是必然事件的是( )
A.车辆随机到达一个路口,遇到红灯
B.同一平面内三条直线相交,交点的个数为3个
C.掷一枚质地均匀的骰子,掷出的点数不超过6
D.用长度分别为的三根小木棒摆成一个三角形
4.小明在高架桥上试驾一辆新能源汽车,以每小时80千米的速度匀速行驶,行驶的路程随时间的变化而变化,在这个变化过程中,自变量是( )
A.汽车 B.路程 C.速度 D.时间
5.小明在坪山区中心公园沿着一条小路散步,小明两次拐弯后方向与原来相同,已知第一次拐的角,第二次拐的角是( )
A. B. C. D.
6.如图,四点在直线上,点在直线外,,若,,,则点到直线的距离是( )
A. B. C. D.
7.如图,在的正方形网格中,线段,的端点均在格点上,则和的数量关系是( )
A. B. C. D.
8.“宝剑锋从磨砺出,梅花香自苦寒来”.已知某种梅花的花粉直径是,这个用科学记数法表示的数据还原为小数是( )
A. B. C. D.
9.将一根长的铁丝按下列四个选项标记的长度剪开,能围成三角形的是( )
A.
B.
C.
D.
10.如图,给出下列条件:,,,,选择其中个条件,不能判断的是( )
A. B. C. D.
二、填空题(6小题,每题3分,共18分)
11.如图,在中,是的垂直平分线.若,,则的周长为 .
12.10名学生,每人做10次抛瓶盖的实验,实验数据如下表:
姓名 小王 小陈 小明 小红 小亮 小朵 小凡 小果 小凯 小梅
盖口向上的次数 6 4 6 7 7 8 9 7 5 8
根据表中数据,可以估计:抛一次瓶盖,落地后盖口向上的概率约为 .
13.若x2+y2=8,xy=2,则(x﹣y)2= .
14.在△ABC中,AB=AD=CD,且∠C=40°,则∠BAD的度数为 .
15.一个角的余角比它的补角的还少,则这个角余角的度数为 .
16.如图,在中,,是的中点,、相交于,设的面积为,的面积为,若的面积为12,则 .
第II卷
北师大版2025—2026学年八年级上册数学入学考试押题试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
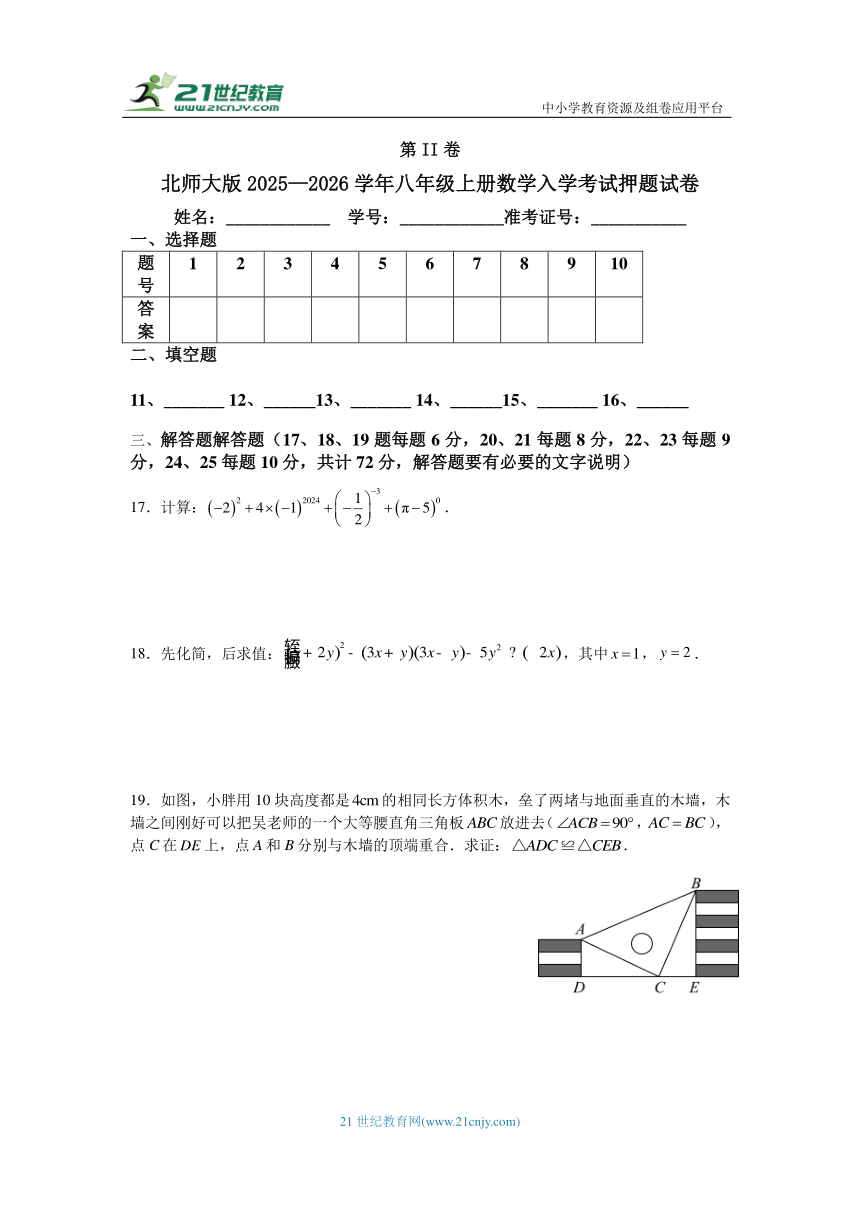
17.计算:.
18.先化简,后求值:,其中,.
19.如图,小胖用10块高度都是的相同长方体积木,垒了两堵与地面垂直的木墙,木墙之间刚好可以把吴老师的一个大等腰直角三角板放进去(,),点C在上,点A和B分别与木墙的顶端重合.求证:.
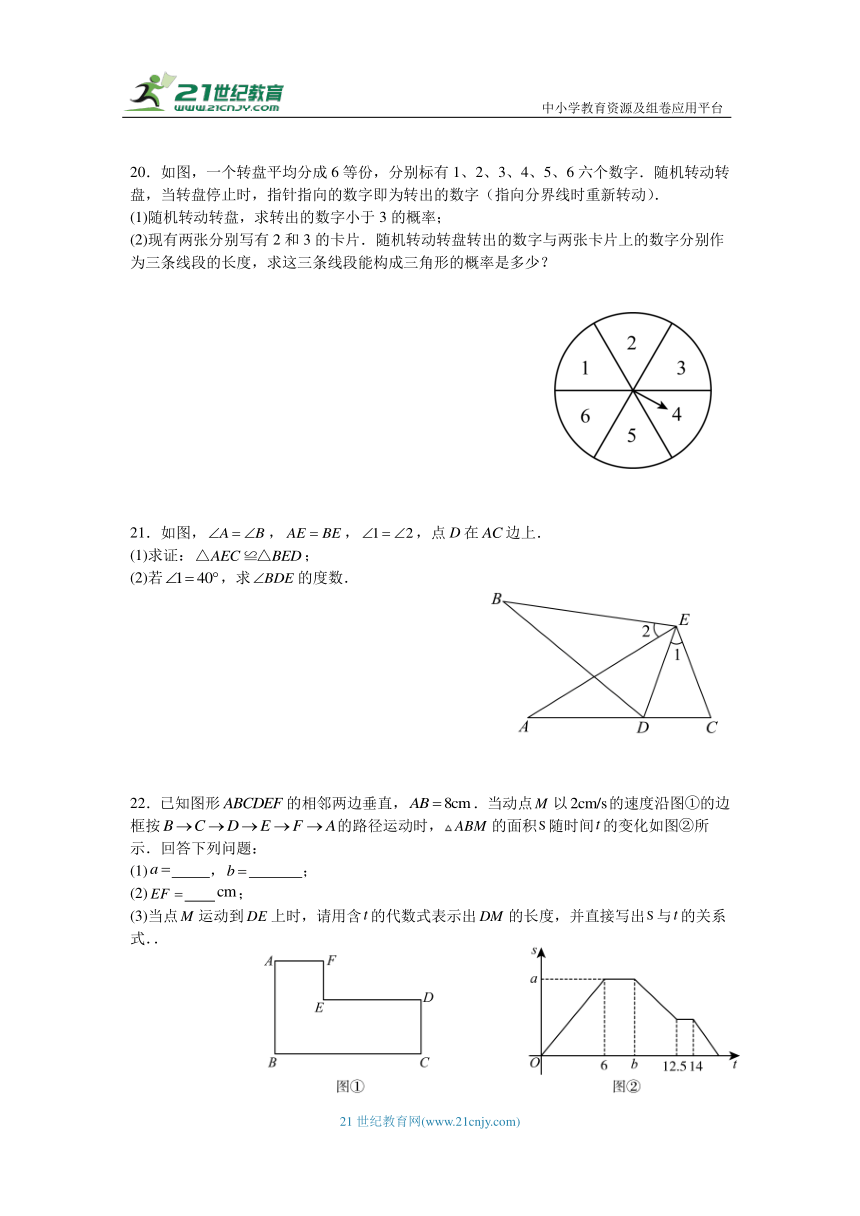
20.如图,一个转盘平均分成6等份,分别标有1、2、3、4、5、6六个数字.随机转动转盘,当转盘停止时,指针指向的数字即为转出的数字(指向分界线时重新转动).
(1)随机转动转盘,求转出的数字小于3的概率;
(2)现有两张分别写有2和3的卡片.随机转动转盘转出的数字与两张卡片上的数字分别作为三条线段的长度,求这三条线段能构成三角形的概率是多少?
21.如图,,,,点D在边上.
(1)求证:;
(2)若,求的度数.
22.已知图形的相邻两边垂直,.当动点以的速度沿图①的边框按的路径运动时,的面积随时间的变化如图②所示.回答下列问题:
(1) , ;
(2) ;
(3)当点运动到上时,请用含的代数式表示出的长度,并直接写出与的关系式..
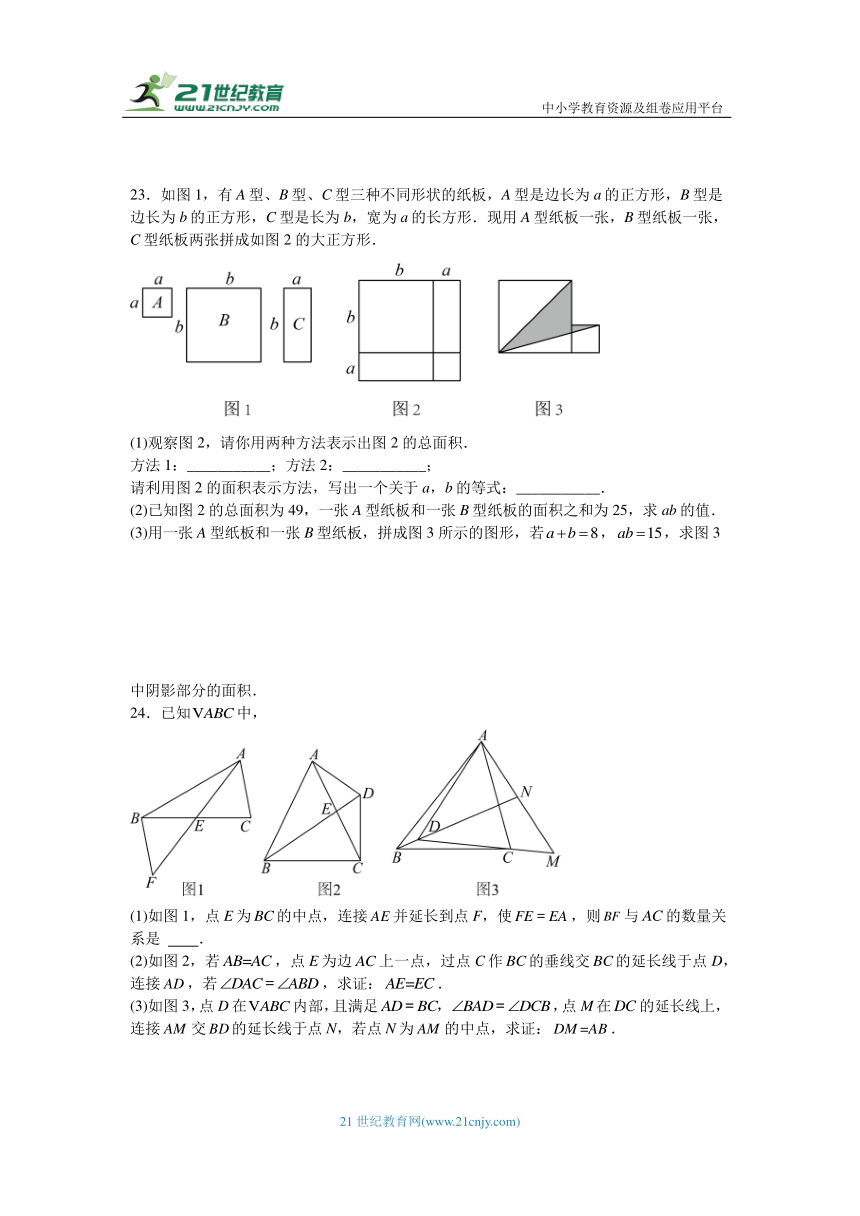
23.如图1,有A型、B型、C型三种不同形状的纸板,A型是边长为a的正方形,B型是边长为b的正方形,C型是长为b,宽为a的长方形.现用A型纸板一张,B型纸板一张,C型纸板两张拼成如图2的大正方形.
(1)观察图2,请你用两种方法表示出图2的总面积.
方法1:___________;方法2:___________;
请利用图2的面积表示方法,写出一个关于a,b的等式:___________.
(2)已知图2的总面积为49,一张A型纸板和一张B型纸板的面积之和为25,求ab的值.
(3)用一张A型纸板和一张B型纸板,拼成图3所示的图形,若,,求图3
中阴影部分的面积.
24.已知中,
(1)如图1,点E为的中点,连接并延长到点F,使,则与的数量关系是 .
(2)如图2,若,点E为边上一点,过点C作的垂线交的延长线于点D,连接,若,求证:.
(3)如图3,点D在内部,且满足,点M在的延长线上,连接交的延长线于点N,若点N为的中点,求证:.
25.综合运用
已知,
(1)化简A和B;
(2)若变量y满足,求出y与x之间的关系式;
(3)在(2)的条件下,求的值.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D D C D B A A A D C
二、填空题
11.【解】解:∵是的垂直平分线,
∴,
∴的周长.
故答案为:14.
12.【解】解:由题意得,,
故答案为:0.67.
13.【解】解:(x﹣y)2=
当x2+y2=8,xy=2,
原式=8-2×2=4
故答案为:4.
14.【解】
故答案为:20°.
15.【解】解:设这个角是,则它的余角为,它的补角为,由题意得:
,
解得:,
∴这个角的余角是:,
故答案为:.
16.【解】解:在中,,是的中点,的面积为12,
的面积为8,的面积为6,
的面积为,的面积为,
.
故答案为:2.
三、解答题
17.【解】解:
.
18.【解】解:
,
当,时,原式.
19.【解】证明:由题意得:,
,
,
,
在和中,
,
∴.
20.【解】(1)解:∵转盘中共有6个数字,小于3的数字有1和2,
∴转出的数字小于3的概率为;
(2)转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,
分别为:123,223,323,423,523,623,
其中能组成三角形的是223,323,423,共3种,
∴这三条线段能构成三角形的概率是.
21.【解】(1)解:∵,
∴,
∴,
在和中
∴.
(2)解:∵,
∴,
∴,
∵,
∴,
∴,
∴.
22.【解】(1)由图2得,5段函数分别是当点在、、、、上时,
第一段当时,点在上,
,
当点在点处时,,即,
第四段当时,点在上,
,
,
,
,
故答案为:48,8.5;
(2)由(1)求出,
故答案为:3;
(3)当点在上时,点的路程为,
,
;
当点在上时,点路程为,
,
,
当点在上时,,
设,把,,代入得,
,
,
.
23.【解】(1)解:用两种方法表示出图2的总面积为和,
关于,的等式,
故答案为:;;;
(2)解:由题意得,,,
;
(3)解:由题意得图3中阴影部分的面积为:
,
当,时,
图3中阴影部分的面积为:
.
24.【解】(1)解:∵点E为的中点,
∴,
在和中,
,
∴,
∴,
故答案为:;
(2)证明:如图2,过点A作于H,过点C作交的延长线于T,
∵,
∴,
在和中,
,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
在和中,
,
∴,
∴,
∴;
(3)证明:过点M作交的延长线于T,交于G,在上取一点K,使得,
连接.
∵,
∴,
在和中,
,
∴,
∴,
∵,
∴,
同理可得:,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴,
∵,
∴.
25.【解】(1)解:
,
(2)解:∵,
∴,
∴;
(3)解:∵,
∴
.
21世纪教育网(www.21cnjy.com)
北师大版2025—2026学年八年级上册数学入学考试押题试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列计算正确的是( )
A. B.
C. D.
2.下列图案中不是轴对称图形的是( )
A.B.C. D.
3.下列事件中,是必然事件的是( )
A.车辆随机到达一个路口,遇到红灯
B.同一平面内三条直线相交,交点的个数为3个
C.掷一枚质地均匀的骰子,掷出的点数不超过6
D.用长度分别为的三根小木棒摆成一个三角形
4.小明在高架桥上试驾一辆新能源汽车,以每小时80千米的速度匀速行驶,行驶的路程随时间的变化而变化,在这个变化过程中,自变量是( )
A.汽车 B.路程 C.速度 D.时间
5.小明在坪山区中心公园沿着一条小路散步,小明两次拐弯后方向与原来相同,已知第一次拐的角,第二次拐的角是( )
A. B. C. D.
6.如图,四点在直线上,点在直线外,,若,,,则点到直线的距离是( )
A. B. C. D.
7.如图,在的正方形网格中,线段,的端点均在格点上,则和的数量关系是( )
A. B. C. D.
8.“宝剑锋从磨砺出,梅花香自苦寒来”.已知某种梅花的花粉直径是,这个用科学记数法表示的数据还原为小数是( )
A. B. C. D.
9.将一根长的铁丝按下列四个选项标记的长度剪开,能围成三角形的是( )
A.
B.
C.
D.
10.如图,给出下列条件:,,,,选择其中个条件,不能判断的是( )
A. B. C. D.
二、填空题(6小题,每题3分,共18分)
11.如图,在中,是的垂直平分线.若,,则的周长为 .
12.10名学生,每人做10次抛瓶盖的实验,实验数据如下表:
姓名 小王 小陈 小明 小红 小亮 小朵 小凡 小果 小凯 小梅
盖口向上的次数 6 4 6 7 7 8 9 7 5 8
根据表中数据,可以估计:抛一次瓶盖,落地后盖口向上的概率约为 .
13.若x2+y2=8,xy=2,则(x﹣y)2= .
14.在△ABC中,AB=AD=CD,且∠C=40°,则∠BAD的度数为 .
15.一个角的余角比它的补角的还少,则这个角余角的度数为 .
16.如图,在中,,是的中点,、相交于,设的面积为,的面积为,若的面积为12,则 .
第II卷
北师大版2025—2026学年八年级上册数学入学考试押题试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.计算:.
18.先化简,后求值:,其中,.
19.如图,小胖用10块高度都是的相同长方体积木,垒了两堵与地面垂直的木墙,木墙之间刚好可以把吴老师的一个大等腰直角三角板放进去(,),点C在上,点A和B分别与木墙的顶端重合.求证:.
20.如图,一个转盘平均分成6等份,分别标有1、2、3、4、5、6六个数字.随机转动转盘,当转盘停止时,指针指向的数字即为转出的数字(指向分界线时重新转动).
(1)随机转动转盘,求转出的数字小于3的概率;
(2)现有两张分别写有2和3的卡片.随机转动转盘转出的数字与两张卡片上的数字分别作为三条线段的长度,求这三条线段能构成三角形的概率是多少?
21.如图,,,,点D在边上.
(1)求证:;
(2)若,求的度数.
22.已知图形的相邻两边垂直,.当动点以的速度沿图①的边框按的路径运动时,的面积随时间的变化如图②所示.回答下列问题:
(1) , ;
(2) ;
(3)当点运动到上时,请用含的代数式表示出的长度,并直接写出与的关系式..
23.如图1,有A型、B型、C型三种不同形状的纸板,A型是边长为a的正方形,B型是边长为b的正方形,C型是长为b,宽为a的长方形.现用A型纸板一张,B型纸板一张,C型纸板两张拼成如图2的大正方形.
(1)观察图2,请你用两种方法表示出图2的总面积.
方法1:___________;方法2:___________;
请利用图2的面积表示方法,写出一个关于a,b的等式:___________.
(2)已知图2的总面积为49,一张A型纸板和一张B型纸板的面积之和为25,求ab的值.
(3)用一张A型纸板和一张B型纸板,拼成图3所示的图形,若,,求图3
中阴影部分的面积.
24.已知中,
(1)如图1,点E为的中点,连接并延长到点F,使,则与的数量关系是 .
(2)如图2,若,点E为边上一点,过点C作的垂线交的延长线于点D,连接,若,求证:.
(3)如图3,点D在内部,且满足,点M在的延长线上,连接交的延长线于点N,若点N为的中点,求证:.
25.综合运用
已知,
(1)化简A和B;
(2)若变量y满足,求出y与x之间的关系式;
(3)在(2)的条件下,求的值.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D D C D B A A A D C
二、填空题
11.【解】解:∵是的垂直平分线,
∴,
∴的周长.
故答案为:14.
12.【解】解:由题意得,,
故答案为:0.67.
13.【解】解:(x﹣y)2=
当x2+y2=8,xy=2,
原式=8-2×2=4
故答案为:4.
14.【解】
故答案为:20°.
15.【解】解:设这个角是,则它的余角为,它的补角为,由题意得:
,
解得:,
∴这个角的余角是:,
故答案为:.
16.【解】解:在中,,是的中点,的面积为12,
的面积为8,的面积为6,
的面积为,的面积为,
.
故答案为:2.
三、解答题
17.【解】解:
.
18.【解】解:
,
当,时,原式.
19.【解】证明:由题意得:,
,
,
,
在和中,
,
∴.
20.【解】(1)解:∵转盘中共有6个数字,小于3的数字有1和2,
∴转出的数字小于3的概率为;
(2)转盘被平均分成6等份,转到每个数字的可能性相等,共有6种可能结果,
分别为:123,223,323,423,523,623,
其中能组成三角形的是223,323,423,共3种,
∴这三条线段能构成三角形的概率是.
21.【解】(1)解:∵,
∴,
∴,
在和中
∴.
(2)解:∵,
∴,
∴,
∵,
∴,
∴,
∴.
22.【解】(1)由图2得,5段函数分别是当点在、、、、上时,
第一段当时,点在上,
,
当点在点处时,,即,
第四段当时,点在上,
,
,
,
,
故答案为:48,8.5;
(2)由(1)求出,
故答案为:3;
(3)当点在上时,点的路程为,
,
;
当点在上时,点路程为,
,
,
当点在上时,,
设,把,,代入得,
,
,
.
23.【解】(1)解:用两种方法表示出图2的总面积为和,
关于,的等式,
故答案为:;;;
(2)解:由题意得,,,
;
(3)解:由题意得图3中阴影部分的面积为:
,
当,时,
图3中阴影部分的面积为:
.
24.【解】(1)解:∵点E为的中点,
∴,
在和中,
,
∴,
∴,
故答案为:;
(2)证明:如图2,过点A作于H,过点C作交的延长线于T,
∵,
∴,
在和中,
,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
在和中,
,
∴,
∴,
∴;
(3)证明:过点M作交的延长线于T,交于G,在上取一点K,使得,
连接.
∵,
∴,
在和中,
,
∴,
∴,
∵,
∴,
同理可得:,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∴,
∴,
∵,
∴.
25.【解】(1)解:
,
(2)解:∵,
∴,
∴;
(3)解:∵,
∴
.
21世纪教育网(www.21cnjy.com)
同课章节目录
