人教版2025—2026学年九年级上册数学第一次月考全真模拟试卷(含答案)
文档属性
| 名称 | 人教版2025—2026学年九年级上册数学第一次月考全真模拟试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 20:11:32 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版2025—2026学年九年级上册数学第一次月考全真模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.如图各交通标志中,不是中心对称图形的是( )
A. B. C. D.
2.下列方程中,属于一元二次方程的是( )
A. B.
C. D.
3.用配方法解方程时,配方后所得的方程为( )
A. B. C. D.
4.点关于原点对称的点的坐标是( )
A. B. C. D.
5.将函数y=2(x+1)2﹣3的图象向上平移2个单位,再向左平移1个单位,可得到的抛物线的解析式为( )
A.y=2(x﹣1)2﹣5 B.y=2x2﹣1
C.y=2(x+2)2﹣5 D.y=2(x+2)2﹣1
6.如图,抛物线与直线相交于点和,若,则的取值范围是( )
A. B. C.或 D.或
7.函数和(为常数,且),在同一平面直角坐标系中的大致图象可能是( )
A. B. C. D.
8.设方程的两个根为α,β, 那么的值等于( )
A. B. C.1 D.3
9.如图,绕点O顺时针旋转到的位置,已知,则等于( )
A. B. C. D.
10.对于二次函数,规定函数是它的相关函数.已知点M,N的坐标分别为,,连接,若线段与二次函数的相关函数的图象有两个公共点,则n的取值范围为( )
A.或 B.或
C.或 D.或
二、填空题(6小题,每题3分,共18分)
11.若关于的方程一个根是1,则另一根为 .
12.如图,在△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,则∠B′AC的度数为 .
13.要修一个圆形喷水池,在池中心竖直安装一根水管,水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为处达到最高,高度为,水柱落地处离池中心,水管高度应为 .
14.已知一个直角三角形的两条直角边长恰好是方程的两根,那么这个直角三角形斜边的长为 .
15.如图,在平面直角坐标系中,抛物线的对称轴为直线,与轴的一个交点为,则关于的方程的两根为 .
16.在平面直角坐标系中,抛物线与轴的一个交点坐标,对称轴为直线,其部分图象如图所示,下列结论:①抛物线过原点;②;③;④抛物线的顶点坐标为;⑤当时,随的增大而增大.其中结论正确的是 .
第II卷
人教版2025—2026学年九年级上册数学第一次月考全真模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
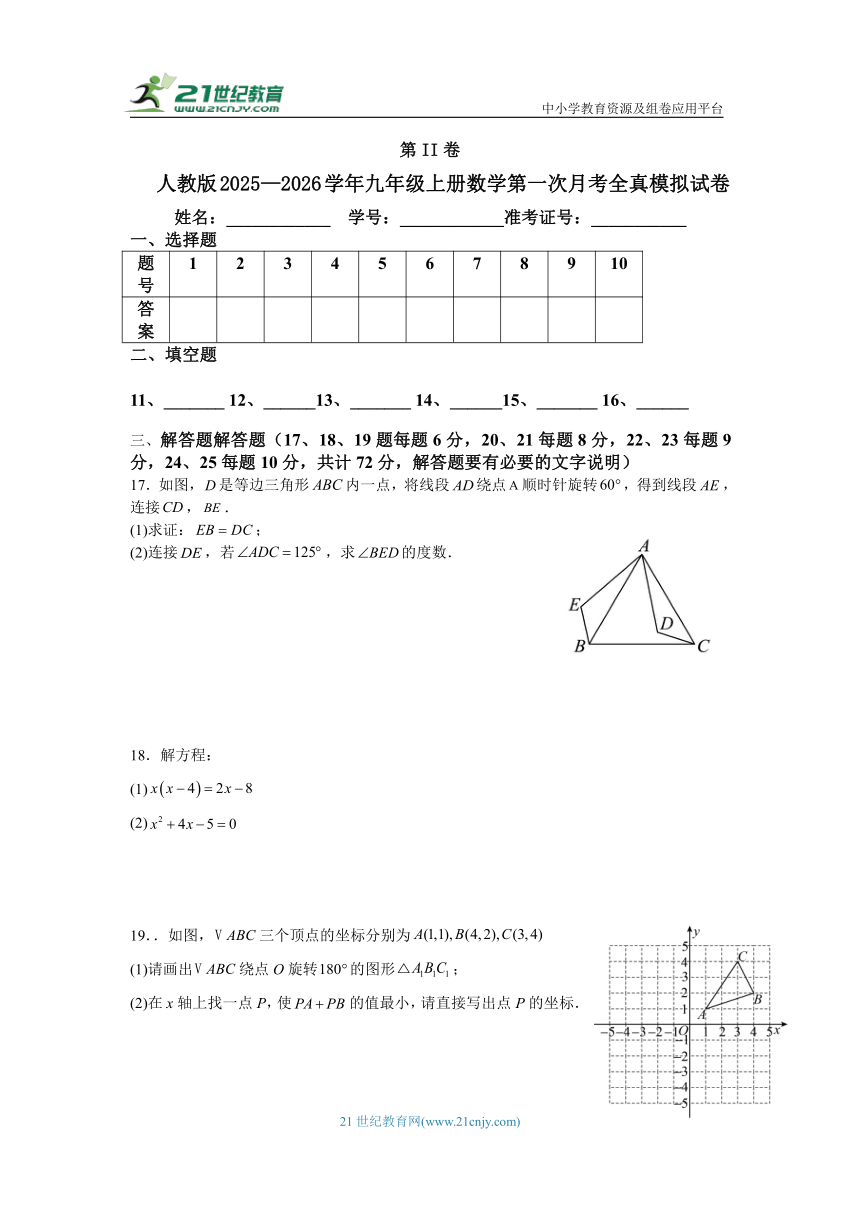
17.如图,是等边三角形内一点,将线段绕点顺时针旋转,得到线段,连接,.
(1)求证:;
(2)连接,若,求的度数.
18.解方程:
(1)
(2)
19..如图,三个顶点的坐标分别为
(1)请画出绕点O旋转的图形;
(2)在x轴上找一点P,使的值最小,请直接写出点P的坐标.
20.如图,在等腰直角中,是边上任意一点(不与重合),将线段绕点逆时针旋转得到线段,连接.
(1)求的度数;
(2)若,求的长.
21.2024年是农历甲辰龙年,含有“龙”元素的饰品深受大众喜爱.商场购进一批单价为70元的“吉祥龙”公仔,并以每个80元售出.由于销售火爆,公仔的销售单价经过两次调整后,上涨到每个125元,此时每天可售出75个.
(1)若销售单价每次上涨的百分率相同,求该百分率;
(2)市场调查发现:销售单价每降低1元,其销售量相应增加5个.那么销售单价应降低多少,才能使每天所获销售利润最大?最大利润是多少?
22.已知关于的一元二次方程.
(1)求证:无论取何值,方程都有两个不相等的实数根;
(2)如果方程的两个实数根为,且,求的值.
23.已知是抛物(b为常数)上的两点,当时,总有
(1)求b的值;
(2)将抛物线平移后得到抛物线.
探究下列问题:
①若抛物线与抛物线有一个交点,求m的取值范围;
②设抛物线与x轴交于A,B两点,与y轴交于点C,抛物线的顶点为点E,外接圆的圆心为点F,如果对抛物线上的任意一点P,在抛物线上总存在一点Q,使得点P、Q的纵坐标相等.求长的取值范围.
24.定义:如果抛物线的顶点在抛物线上,抛物线的顶点也在抛物线上,且抛物线与的顶点不重合,我们称抛物线与互为“伴随抛物线”.
(1)判断下列抛物线是否为抛物线的“伴随抛物线”,是的打“ √”,不是的打“ ”:
① ___;② ___;③ ___
(2)若抛物线(为实数且)与互为“伴随抛物线”,请问抛物线的图象是否经过定点?若经过,求出定点的坐标,否则,请说明理由;
(3)已知抛物线(为实数且)与轴交于点,抛物线:与轴交于点,若抛物线与互为“伴随抛物线”,且,请问是否为定值,若是,求出这个值; 若不是,请说明理由.
25.如图, 抛物线交x轴于点A、B两点,与y轴交于点,其顶点为点D.
(1)求a的值和顶点 D 的坐标;
(2)在x轴上有一动点,若点C、D以M为中心对称的对称点分别是、,请判断以C、D、、为顶点的四边形可能是正方形吗? 若存在,求出对应的点M的坐标; 若不存在,请说明理由;
(3)若N是直线 上的一动点,把绕点N旋转 ,原点O的对应点为,若点 恰好落在抛物线上,请求出所有符合条件的点N的坐标.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 A B D D D C D A D A
二、填空题
11.【解】解:由题意得:,
关于的方程一个根是1,
,
故答案为:.
12.【解】解:∵∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,
∴∠B′AC′=33°,∠BAB′=50°,
∴∠B′AC的度数=50° 33°=17°.
故答案为17°.
13.【解】解:设抛物线的解析式为
由题意可知抛物线的顶点坐标为,与轴的一个交点为,
,
解得:,
抛物线的解析式为:,
当时,,
水管的高度为,
故答案为:.
14.【解】∵,
∴,
∴,
∴直角三角形的两条直角边长分别为、,
∴这个直角三角形斜边的长为,
故答案为:.
15.【解】解:∵抛物线的对称轴为直线,与轴的一个交点为,
∴抛物线与轴的另一个交点坐标为,
∴关于的方程的解为,,
故答案为:,.
16.【解】解:抛物线与轴的一个交点坐标为,对称轴是直线,
抛物线与轴的另一个交点坐标为,因此①正确;
当时,,
由图象可知此时,即,因此②不正确;
对称轴是直线,即,
∴,而,
∴,故③正确;
对称轴是直线,即,
∴,而,
∴当时,,
∴顶点为,因此④正确;
在对称轴的左侧,随的增大而减小,
即:当时,随的增大而减小,因此⑤不正确;
综上所述,正确的结论有①③④,
故答案为:①③④.
三、解答题
17.【解】(1)证明:是等边三角形,
,,
将线段绕点顺时针旋转,得到线段,
,,
,
,
在和中,
,
,
;
(2)如图,连接,
,,
为等边三角形,
,
又,
,
.
18.【解】(1)解:,
,
,
,
令或,
解得:,;
(2)解:,
,
令或,
解得:,.
19.【解】(1)解: 如图所示,即为所求;
(2)解:作A点关于x轴的对称点,连接交x轴于点P,点P即为所求,
∴P点坐标为.
∴所围成的矩形燃放地面积不能为平方米,
21.【解】(1)解:设每次上涨的百分率为,列方程为:
,
解得:,(舍去),
答:每次上涨的百分率为;
(2)解:设销售单价降低元,销售利润为元,
,
∴当销售单价降低元,所获销售利润最大,最大为元.
22.【解】(1)证明:,
∵无论取何值,,恒成立,
∴无论取何值,方程都有两个不相等的实数根.
(2)解:∵是方程的两个实数根,
∴,,
∴,
解得:或.
23.【解】(1)解:由题可知:
时,总有,
.
则,
∴,
∴总成立,且,
;
(2)①注意到抛物线最大值和开口大小不变,m只影响图象左右平移下面考虑满足题意的两种临界情形:
(i)当抛物线过点时,如图所示,
此时,,解得或(舍).
(ii)当抛物线过点时,如图所示,
此时,,
解得或(舍),
综上,,
②同①考虑满足题意的两种临界情形:
(i)当抛物线过点时,如图所示,
此时,,解得或(舍).
(ii)当抛物线过点时,如图所示,
此时,,解得或0(舍).
综上,
如图,由圆的性质可知,点E、F在线段的垂直平分线上.
令,解得,
,
,
,
设,
,
,
,
,
,即,
.
,即,
,
24.【解】(1)解:二次函数的顶点坐标为,则有:
①把点代入明显成立,而二次函数的顶点坐标为,代入明显成立;故与是“伴随抛物线”;
②把点代入明显不成立,故与不是“伴随抛物线”;
③把点代入明显成立,而二次函数的顶点坐标为,代入明显成立;故与是“伴随抛物线”;
故答案为√,×,√;
(2)解:∵,
的顶点坐标为,
∵抛物线与互为“伴随抛物线”,
点在抛物线上,
∴,化简得,
抛物线化简为:,
令,
解得或,
抛物线过定点,坐标为、;
(3)解:抛物线,
∴抛物线的顶点为,
抛物线与互为“伴随抛物线”,
点在抛物线上,
∴,
化简得①,
∵,
∴,
代入①得:②,
抛物线与轴交于点,
∴是关于的一元二次方程的两根,
∴,
∵
,
同理可得,
,
为定值,定值为4.
25.【解】(1)解:将点代入解析式得,,解得,
∴ ,
则点;
(2)解:存在,理由如下,
∵点在x轴上,
∴点只能在x轴上方,点只能在x轴下方,
则四边形只能为,即对角线和相等,且关于点M对称,
∴,,
∵四边形为正方形,
∴ ,
∴ ,
即,解得,
故存在点M使得以C、D、 为顶点的四边形是正方形,点;
(3)解:令,则,解得或,则点,,
①当把绕点N逆时针旋转 ,原点O的对应点为,
∴,,
连接,过点作,如图,
则为等腰直角三角形,,
∵,
∴,
∴,
则,
设,则点,
∵点 恰好落在抛物线上,
∴,化简得,解得,
那么, ,;
②当把绕点N顺时针旋转 ,原点O的对应点为,
∴,,
过点作,如图,
同理可证,
则,
设,则点,
∵点 恰好落在抛物线上,
∴,化简得,解得,
那么, ,;
故所有符合条件的点N的坐标,,,.
21世纪教育网(www.21cnjy.com)
人教版2025—2026学年九年级上册数学第一次月考全真模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.如图各交通标志中,不是中心对称图形的是( )
A. B. C. D.
2.下列方程中,属于一元二次方程的是( )
A. B.
C. D.
3.用配方法解方程时,配方后所得的方程为( )
A. B. C. D.
4.点关于原点对称的点的坐标是( )
A. B. C. D.
5.将函数y=2(x+1)2﹣3的图象向上平移2个单位,再向左平移1个单位,可得到的抛物线的解析式为( )
A.y=2(x﹣1)2﹣5 B.y=2x2﹣1
C.y=2(x+2)2﹣5 D.y=2(x+2)2﹣1
6.如图,抛物线与直线相交于点和,若,则的取值范围是( )
A. B. C.或 D.或
7.函数和(为常数,且),在同一平面直角坐标系中的大致图象可能是( )
A. B. C. D.
8.设方程的两个根为α,β, 那么的值等于( )
A. B. C.1 D.3
9.如图,绕点O顺时针旋转到的位置,已知,则等于( )
A. B. C. D.
10.对于二次函数,规定函数是它的相关函数.已知点M,N的坐标分别为,,连接,若线段与二次函数的相关函数的图象有两个公共点,则n的取值范围为( )
A.或 B.或
C.或 D.或
二、填空题(6小题,每题3分,共18分)
11.若关于的方程一个根是1,则另一根为 .
12.如图,在△ABC中,∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,则∠B′AC的度数为 .
13.要修一个圆形喷水池,在池中心竖直安装一根水管,水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为处达到最高,高度为,水柱落地处离池中心,水管高度应为 .
14.已知一个直角三角形的两条直角边长恰好是方程的两根,那么这个直角三角形斜边的长为 .
15.如图,在平面直角坐标系中,抛物线的对称轴为直线,与轴的一个交点为,则关于的方程的两根为 .
16.在平面直角坐标系中,抛物线与轴的一个交点坐标,对称轴为直线,其部分图象如图所示,下列结论:①抛物线过原点;②;③;④抛物线的顶点坐标为;⑤当时,随的增大而增大.其中结论正确的是 .
第II卷
人教版2025—2026学年九年级上册数学第一次月考全真模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.如图,是等边三角形内一点,将线段绕点顺时针旋转,得到线段,连接,.
(1)求证:;
(2)连接,若,求的度数.
18.解方程:
(1)
(2)
19..如图,三个顶点的坐标分别为
(1)请画出绕点O旋转的图形;
(2)在x轴上找一点P,使的值最小,请直接写出点P的坐标.
20.如图,在等腰直角中,是边上任意一点(不与重合),将线段绕点逆时针旋转得到线段,连接.
(1)求的度数;
(2)若,求的长.
21.2024年是农历甲辰龙年,含有“龙”元素的饰品深受大众喜爱.商场购进一批单价为70元的“吉祥龙”公仔,并以每个80元售出.由于销售火爆,公仔的销售单价经过两次调整后,上涨到每个125元,此时每天可售出75个.
(1)若销售单价每次上涨的百分率相同,求该百分率;
(2)市场调查发现:销售单价每降低1元,其销售量相应增加5个.那么销售单价应降低多少,才能使每天所获销售利润最大?最大利润是多少?
22.已知关于的一元二次方程.
(1)求证:无论取何值,方程都有两个不相等的实数根;
(2)如果方程的两个实数根为,且,求的值.
23.已知是抛物(b为常数)上的两点,当时,总有
(1)求b的值;
(2)将抛物线平移后得到抛物线.
探究下列问题:
①若抛物线与抛物线有一个交点,求m的取值范围;
②设抛物线与x轴交于A,B两点,与y轴交于点C,抛物线的顶点为点E,外接圆的圆心为点F,如果对抛物线上的任意一点P,在抛物线上总存在一点Q,使得点P、Q的纵坐标相等.求长的取值范围.
24.定义:如果抛物线的顶点在抛物线上,抛物线的顶点也在抛物线上,且抛物线与的顶点不重合,我们称抛物线与互为“伴随抛物线”.
(1)判断下列抛物线是否为抛物线的“伴随抛物线”,是的打“ √”,不是的打“ ”:
① ___;② ___;③ ___
(2)若抛物线(为实数且)与互为“伴随抛物线”,请问抛物线的图象是否经过定点?若经过,求出定点的坐标,否则,请说明理由;
(3)已知抛物线(为实数且)与轴交于点,抛物线:与轴交于点,若抛物线与互为“伴随抛物线”,且,请问是否为定值,若是,求出这个值; 若不是,请说明理由.
25.如图, 抛物线交x轴于点A、B两点,与y轴交于点,其顶点为点D.
(1)求a的值和顶点 D 的坐标;
(2)在x轴上有一动点,若点C、D以M为中心对称的对称点分别是、,请判断以C、D、、为顶点的四边形可能是正方形吗? 若存在,求出对应的点M的坐标; 若不存在,请说明理由;
(3)若N是直线 上的一动点,把绕点N旋转 ,原点O的对应点为,若点 恰好落在抛物线上,请求出所有符合条件的点N的坐标.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 A B D D D C D A D A
二、填空题
11.【解】解:由题意得:,
关于的方程一个根是1,
,
故答案为:.
12.【解】解:∵∠BAC=33°,将△ABC绕点A按顺时针方向旋转50°,对应得到△AB′C′,
∴∠B′AC′=33°,∠BAB′=50°,
∴∠B′AC的度数=50° 33°=17°.
故答案为17°.
13.【解】解:设抛物线的解析式为
由题意可知抛物线的顶点坐标为,与轴的一个交点为,
,
解得:,
抛物线的解析式为:,
当时,,
水管的高度为,
故答案为:.
14.【解】∵,
∴,
∴,
∴直角三角形的两条直角边长分别为、,
∴这个直角三角形斜边的长为,
故答案为:.
15.【解】解:∵抛物线的对称轴为直线,与轴的一个交点为,
∴抛物线与轴的另一个交点坐标为,
∴关于的方程的解为,,
故答案为:,.
16.【解】解:抛物线与轴的一个交点坐标为,对称轴是直线,
抛物线与轴的另一个交点坐标为,因此①正确;
当时,,
由图象可知此时,即,因此②不正确;
对称轴是直线,即,
∴,而,
∴,故③正确;
对称轴是直线,即,
∴,而,
∴当时,,
∴顶点为,因此④正确;
在对称轴的左侧,随的增大而减小,
即:当时,随的增大而减小,因此⑤不正确;
综上所述,正确的结论有①③④,
故答案为:①③④.
三、解答题
17.【解】(1)证明:是等边三角形,
,,
将线段绕点顺时针旋转,得到线段,
,,
,
,
在和中,
,
,
;
(2)如图,连接,
,,
为等边三角形,
,
又,
,
.
18.【解】(1)解:,
,
,
,
令或,
解得:,;
(2)解:,
,
令或,
解得:,.
19.【解】(1)解: 如图所示,即为所求;
(2)解:作A点关于x轴的对称点,连接交x轴于点P,点P即为所求,
∴P点坐标为.
∴所围成的矩形燃放地面积不能为平方米,
21.【解】(1)解:设每次上涨的百分率为,列方程为:
,
解得:,(舍去),
答:每次上涨的百分率为;
(2)解:设销售单价降低元,销售利润为元,
,
∴当销售单价降低元,所获销售利润最大,最大为元.
22.【解】(1)证明:,
∵无论取何值,,恒成立,
∴无论取何值,方程都有两个不相等的实数根.
(2)解:∵是方程的两个实数根,
∴,,
∴,
解得:或.
23.【解】(1)解:由题可知:
时,总有,
.
则,
∴,
∴总成立,且,
;
(2)①注意到抛物线最大值和开口大小不变,m只影响图象左右平移下面考虑满足题意的两种临界情形:
(i)当抛物线过点时,如图所示,
此时,,解得或(舍).
(ii)当抛物线过点时,如图所示,
此时,,
解得或(舍),
综上,,
②同①考虑满足题意的两种临界情形:
(i)当抛物线过点时,如图所示,
此时,,解得或(舍).
(ii)当抛物线过点时,如图所示,
此时,,解得或0(舍).
综上,
如图,由圆的性质可知,点E、F在线段的垂直平分线上.
令,解得,
,
,
,
设,
,
,
,
,
,即,
.
,即,
,
24.【解】(1)解:二次函数的顶点坐标为,则有:
①把点代入明显成立,而二次函数的顶点坐标为,代入明显成立;故与是“伴随抛物线”;
②把点代入明显不成立,故与不是“伴随抛物线”;
③把点代入明显成立,而二次函数的顶点坐标为,代入明显成立;故与是“伴随抛物线”;
故答案为√,×,√;
(2)解:∵,
的顶点坐标为,
∵抛物线与互为“伴随抛物线”,
点在抛物线上,
∴,化简得,
抛物线化简为:,
令,
解得或,
抛物线过定点,坐标为、;
(3)解:抛物线,
∴抛物线的顶点为,
抛物线与互为“伴随抛物线”,
点在抛物线上,
∴,
化简得①,
∵,
∴,
代入①得:②,
抛物线与轴交于点,
∴是关于的一元二次方程的两根,
∴,
∵
,
同理可得,
,
为定值,定值为4.
25.【解】(1)解:将点代入解析式得,,解得,
∴ ,
则点;
(2)解:存在,理由如下,
∵点在x轴上,
∴点只能在x轴上方,点只能在x轴下方,
则四边形只能为,即对角线和相等,且关于点M对称,
∴,,
∵四边形为正方形,
∴ ,
∴ ,
即,解得,
故存在点M使得以C、D、 为顶点的四边形是正方形,点;
(3)解:令,则,解得或,则点,,
①当把绕点N逆时针旋转 ,原点O的对应点为,
∴,,
连接,过点作,如图,
则为等腰直角三角形,,
∵,
∴,
∴,
则,
设,则点,
∵点 恰好落在抛物线上,
∴,化简得,解得,
那么, ,;
②当把绕点N顺时针旋转 ,原点O的对应点为,
∴,,
过点作,如图,
同理可证,
则,
设,则点,
∵点 恰好落在抛物线上,
∴,化简得,解得,
那么, ,;
故所有符合条件的点N的坐标,,,.
21世纪教育网(www.21cnjy.com)
同课章节目录
