人教版2025—2026学年九年级上册数学第一次月考模拟试卷(含答案)
文档属性
| 名称 | 人教版2025—2026学年九年级上册数学第一次月考模拟试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1007.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 18:52:08 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版2025—2026学年九年级上册数学第一次月考模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。笞卷前,考生务必
将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,把答案填写在答题卡上对应题目的位置
,填空题填写在答题卡相应的位置写在本试卷上无效。
3.回答第II卷时,将答案写在第II卷答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列图形中,是中心对称图形的是( )
A.B.C. D.
2.抛物线的对称轴是( )
A.直线 B.直线 C.直线 D.直线
3.如图,将绕着点C顺时针旋转50°后得到,若,则∠BCA的度数是( )
A.120° B.30° C.20° D.10°
4.某公司今年销售一种产品,一月份获得利润5万元,由于产品畅销,利润逐月增加,一月份到二月份的增长率为x,二月份到三月份的增长率是,若三月份获得利润为7.8万元,则可列出方程为( )
A. B.
C. D.
5.将抛物线向下平移2个单位后,所得新抛物线的顶点式为( )
A. B. C. D.
6.已知是方程的两个根,则的值为( )
A. B.3 C. D.
7.设A(﹣2,y1),B(﹣1,y2),C(2,y3)是抛物线y=﹣(x+1)2+1上的三点,则y1,y2,y3的大小关系为( )
A.y2>y1>y3 B.y1>y3>y2 C.y3>y2>y1 D.y3>y1>y2
8.2022年北京冬奥会女子冰壶比赛有若干支队伍参加了单循环比赛,单循环比赛共进行了45场,共有多少支队伍参加比赛?( )
A.8 B.10 C.7 D.9
9.二次函数的图象如图所示,对称轴是直线,则过点和点的直线一定不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.对于二次函数,规定函数是它的相关函数.已知点的坐标分别为,,连接,若线段与二次函数的相关函数的图象有两个公共点,则n的取值范围为( )
A.或 B.或
C.或 D.或
二、填空题(6小题,每题3分,共18分)
11.如图,某小区要在长为,宽为的矩形空地上建造一个花坛,使花坛四周小路的宽度相等,且花坛所占面积为空地面积的一半,则小路宽为 .
12.在平面直角坐标系中,点关于原点的对称点的坐标是 .
13.关于x的一元二次方程(k-1)x2-2x+1=0有两个不相等的实数根,则实数k的取值范围是 .
14.若关于的一元二次方程的常数项为,则 .
15.如图,是绕点O顺时针旋转后得到的图形,点C恰好落在边上,若,则 .
16.如图,在中,,,,将绕点逆时针旋转得到,使点落在边上,连接.则的长为 .
第II卷
人教版2025—2026学年九年级上册数学第一次月考模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
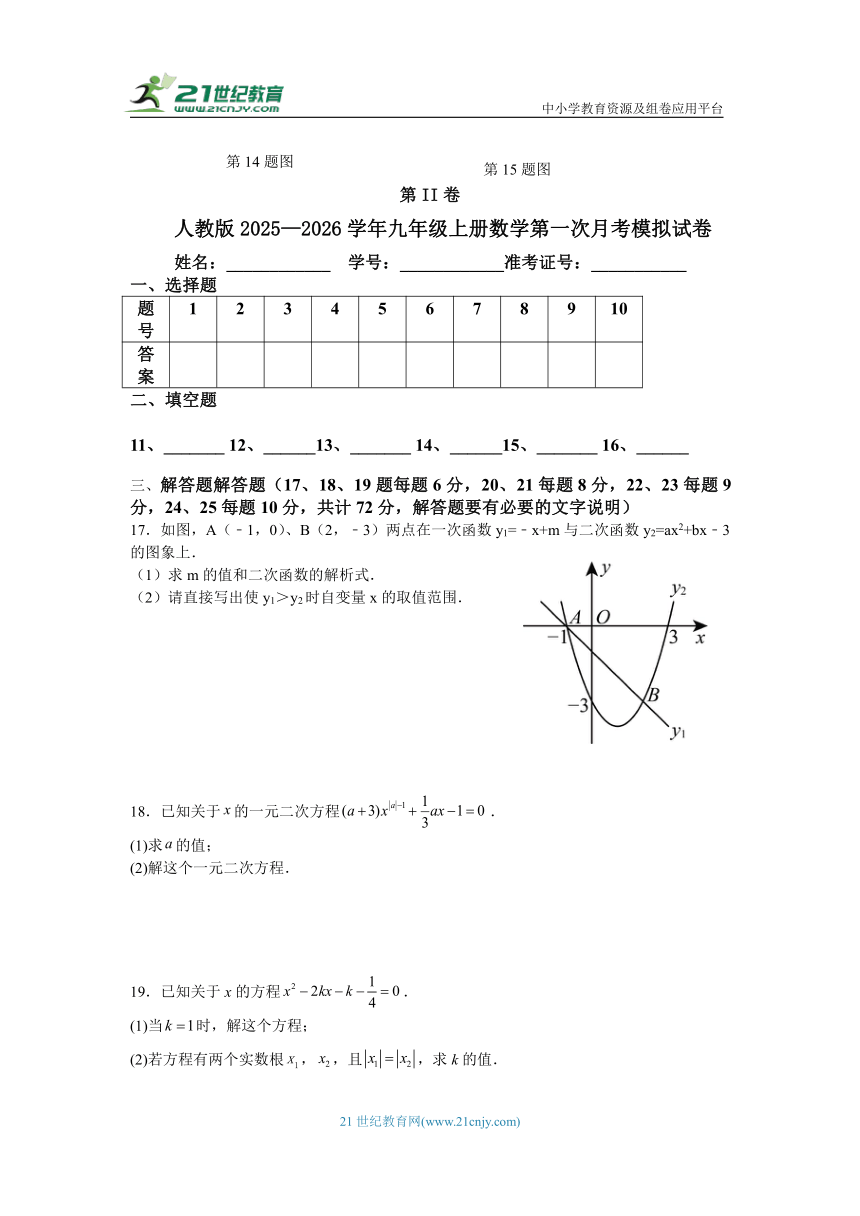
17.如图,A(﹣1,0)、B(2,﹣3)两点在一次函数y1=﹣x+m与二次函数y2=ax2+bx﹣3的图象上.
(1)求m的值和二次函数的解析式.
(2)请直接写出使y1>y2时自变量x的取值范围.
18.已知关于的一元二次方程.
(1)求的值;
(2)解这个一元二次方程.
19.已知关于x的方程.
(1)当时,解这个方程;
(2)若方程有两个实数根,,且,求k的值.
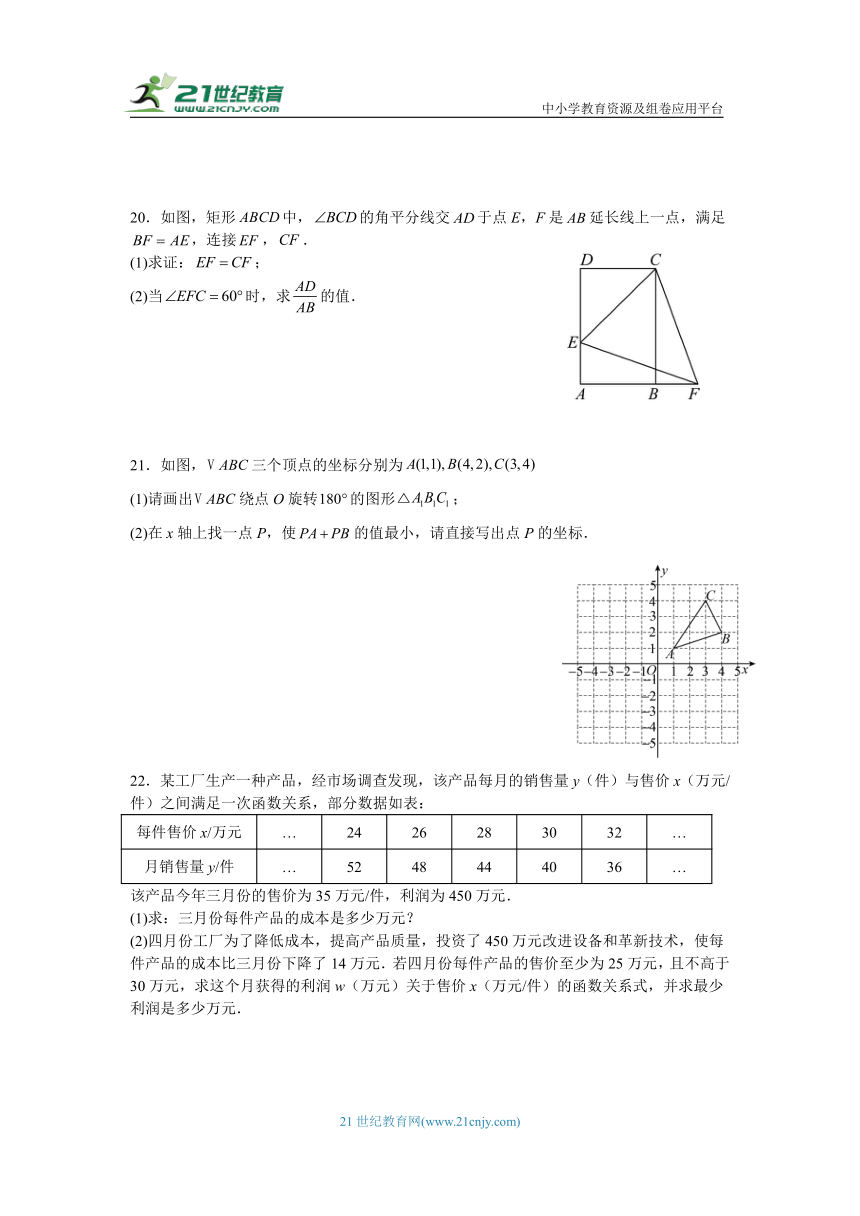
20.如图,矩形中,的角平分线交于点E,F是延长线上一点,满足,连接,.
(1)求证:;
(2)当时,求的值.
21.如图,三个顶点的坐标分别为
(1)请画出绕点O旋转的图形;
(2)在x轴上找一点P,使的值最小,请直接写出点P的坐标.
22.某工厂生产一种产品,经市场调查发现,该产品每月的销售量y(件)与售价x(万元/件)之间满足一次函数关系,部分数据如表:
每件售价x/万元 … 24 26 28 30 32 …
月销售量y/件 … 52 48 44 40 36 …
该产品今年三月份的售价为35万元/件,利润为450万元.
(1)求:三月份每件产品的成本是多少万元?
(2)四月份工厂为了降低成本,提高产品质量,投资了450万元改进设备和革新技术,使每件产品的成本比三月份下降了14万元.若四月份每件产品的售价至少为25万元,且不高于30万元,求这个月获得的利润w(万元)关于售价x(万元/件)的函数关系式,并求最少利润是多少万元.
23.在平面直角坐标系中,若关于的函数的图像记为,将的图像绕着原点旋转得到图像,我们把和合起来的总图像称为 的“青一对称”图像.
(1)若在 的“青一对称”图像上,则 ;
(2)若在 的“青一对称”图像上,求的值;
(3)当二次函数的“青一对称”图像与直线有且只有三个交点时,请求出的值或取值范围.
24.如图,已知抛物线经过两点,直线是抛物线的对称轴.
(1)求抛物线的函数解析式及顶点的坐标;
(2)设点是直线上的一个动点,当时,求点的坐标;
(3)已知与抛物线相交于点,连接,若,求的值.
25.定义:函数图象上的点的纵坐标与横坐标的差叫做点的“双减差”,图象上所有点的“双减差”中最小值称为函数图象的“幸福值”如:抛物线上有点,则点的“双减差”为12;而抛物线上所有点的“双减差”,即该抛物线的“幸福值”为.根据定义,解答下列问题:
(1)已知函数图象上点的横坐标,求点的“双减差”的值;
(2)若直线的“幸福值”为,求的值;
(3)设抛物线顶点的横坐标为,且该抛物线的顶点在直线上,当时,抛物线的“幸福值”是5,求该抛物线的解析式.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 A A B D A A A B C A
二、填空题
11.【解】解:设小路的宽为,则长方形花坛的长为,宽为,
由题意得,,
同理得,
解得或(舍去),
∴小路的宽为,
故答案为:.
12.【解】解:点关于原点对称点的坐标是.
故答案为:.
13.【解】解:∵关于x的一元二次方程(k-1)x2-2x+1=0有两个不相等的实数根,
∴k-1≠0且 =(-2)2-4(k-1)>0,
解得:k<2且k≠1.
故答案为:k<2且k≠1.
14.【解】解:∵常数项为0,
∴,
解得:或2,
又∵,即,
∴.
15.【解】解:∵是绕点O顺时针旋转后得到的图形,
∴,,
∴,
∴,
故答案为:.
16.【解】解:在中,,,
故,
由旋转的性质可知:,,
∴,
在中,,,
故.
故答案为:.
三、解答题
17.【解】(1)由于A(﹣1,0)在一次函数y1=﹣x+m的图象上,得:
﹣(﹣1)+m=0,即m=﹣1;
已知A(﹣1,0)、B(2,﹣3)在二次函数y2=ax2+bx﹣3的图象上,则有:
,解得
∴二次函数的解析式为y2=x2﹣2x﹣3;
(2)由两个函数的图象知:当y1>y2时,﹣1<x<2.
18.【解】(1)解:依题意,得,
解得.
∴a的值为3.
(2)解:把代入原方程,得,
,
,
解得,.
19.【解】(1)解:当时,方程化为,
配方得,
∴,
解得,.
(2)解:,
方程总有实数根,
又,
或,
当时,,解得;
当时,则,解得;
或0.
20.【解】(1)证明:矩形中,,,,
平分,
,又,
,又,
,即,
又,,
,
;
(2)解:,且,
为等边三角形,
,设,,
则,,
,整理得,
故,开方得,又,
,
.
21.【解】(1)解: 如图所示,即为所求;
(2)解:作A点关于x轴的对称点,连接交x轴于点P,点P即为所求,
∴P点坐标为.
22.【解】(1)解:设y与x的函数关系式为,将,代入,得:
,
解得,
∴y与x的函数关系式为;
将代入,得(件),
设三月份每件产品的成本是a万元,
由题意得,
解得,
即三月份每件产品的成本是20万元;
(2)解:四月份每件产品的成本比三月份下降了14万元,则此时的成本为,
由题意得:
,
则抛物线的对称轴为,且,开口向下,
则时,取得最小值,
此时,,
即四月份最少利润是500万元.
23.【解】(1)解:由题意得:图像的函数解析式为,
当时,,
,
故答案为:;
(2)解:,
顶点坐标为,
图像的顶点坐标为,
的解析式为,
在 的“青一对称”图像上,
当时,,
解得:或(舍去),
当时,,
解得:或,
的值为或或;
(3)解:,
顶点坐标为,
将的图像绕着原点旋转得到图像,
的顶点坐标为,
的解析式为,
①当直线与:相切时,即直线与的图像只有一个交点,则,
整理得:,
,
解得:,
此时的解析式为:,
联立直线与的解析式得:,
整理得:,
此时,
直线与的图像只有两个交点,
当时,二次函数的“青一对称”图像与直线有且只有三个交点;
②当时, 的解析式为,的解析式为,
联立直线与的解析式得:,
解得:或(不合题意,舍去),
此时直线与的图像只有一个交点,
联立直线与的解析式得:,
解得:或,
当时,的图像与直线有两个交点和,
当时,二次函数的“青一对称”图像与直线只有三个交点;
当时,的解析式为,的解析式为,
联立直线与的解析式得:,
解得:或,
此时直线与的图像只有两个交点和,
联立直线与的解析式得:,
解得:或,
此时直线与的图像只有两个交点和,,
当时,二次函数的“青一对称”图像与直线有四个交点;
当时,二次函数的“青一对称”图像与直线有且只有三个交点;
综上所述,的值或取值范围是或.
24.【解】(1)解:把代入,得,
解得,
抛物线的函数解析式为,
,
顶点的坐标为;
(2)解:设,则,
当时,,
解得,
;
(3)解:延长交轴于,
设,在中,,
即,
解得,
,
设直线的解析式为,
代入,得,
解得,
的解析式为,
联立,
解得(舍去),,
,
.
25.【解】(1)解:将代入得:,
∴
∴点的“双减差”的值为:
(2)解:由得:,
∵,
∴,
∴随的增大而增大.
故:当时,有最小值,且最小值为:,
∴,
解得:(舍去)
∴
(3)解:由题意得:抛物线的顶点坐标为:,
∴
∴
令,则其对称轴为直线;
∵,
∴,即:;
,此时(不符合题意);
,即:,
此时,当,取最小值,
则,
解得:(舍去),
∴;
,即:,
此时,当,取最小值,
则,
解得:(舍去),
综上所述,该抛物线的解析式为:;
21世纪教育网(www.21cnjy.com)
人教版2025—2026学年九年级上册数学第一次月考模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
注意事项:
1.本试卷分第I卷(选择题)和第II卷(非选择题)两部分。笞卷前,考生务必
将自己的姓名、准考证号填写在答题卡上。
2.回答第I卷时,选出每小题答案后,把答案填写在答题卡上对应题目的位置
,填空题填写在答题卡相应的位置写在本试卷上无效。
3.回答第II卷时,将答案写在第II卷答题卡上。
4.考试结束后,将本试卷和答题卡一并交回。
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.下列图形中,是中心对称图形的是( )
A.B.C. D.
2.抛物线的对称轴是( )
A.直线 B.直线 C.直线 D.直线
3.如图,将绕着点C顺时针旋转50°后得到,若,则∠BCA的度数是( )
A.120° B.30° C.20° D.10°
4.某公司今年销售一种产品,一月份获得利润5万元,由于产品畅销,利润逐月增加,一月份到二月份的增长率为x,二月份到三月份的增长率是,若三月份获得利润为7.8万元,则可列出方程为( )
A. B.
C. D.
5.将抛物线向下平移2个单位后,所得新抛物线的顶点式为( )
A. B. C. D.
6.已知是方程的两个根,则的值为( )
A. B.3 C. D.
7.设A(﹣2,y1),B(﹣1,y2),C(2,y3)是抛物线y=﹣(x+1)2+1上的三点,则y1,y2,y3的大小关系为( )
A.y2>y1>y3 B.y1>y3>y2 C.y3>y2>y1 D.y3>y1>y2
8.2022年北京冬奥会女子冰壶比赛有若干支队伍参加了单循环比赛,单循环比赛共进行了45场,共有多少支队伍参加比赛?( )
A.8 B.10 C.7 D.9
9.二次函数的图象如图所示,对称轴是直线,则过点和点的直线一定不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.对于二次函数,规定函数是它的相关函数.已知点的坐标分别为,,连接,若线段与二次函数的相关函数的图象有两个公共点,则n的取值范围为( )
A.或 B.或
C.或 D.或
二、填空题(6小题,每题3分,共18分)
11.如图,某小区要在长为,宽为的矩形空地上建造一个花坛,使花坛四周小路的宽度相等,且花坛所占面积为空地面积的一半,则小路宽为 .
12.在平面直角坐标系中,点关于原点的对称点的坐标是 .
13.关于x的一元二次方程(k-1)x2-2x+1=0有两个不相等的实数根,则实数k的取值范围是 .
14.若关于的一元二次方程的常数项为,则 .
15.如图,是绕点O顺时针旋转后得到的图形,点C恰好落在边上,若,则 .
16.如图,在中,,,,将绕点逆时针旋转得到,使点落在边上,连接.则的长为 .
第II卷
人教版2025—2026学年九年级上册数学第一次月考模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.如图,A(﹣1,0)、B(2,﹣3)两点在一次函数y1=﹣x+m与二次函数y2=ax2+bx﹣3的图象上.
(1)求m的值和二次函数的解析式.
(2)请直接写出使y1>y2时自变量x的取值范围.
18.已知关于的一元二次方程.
(1)求的值;
(2)解这个一元二次方程.
19.已知关于x的方程.
(1)当时,解这个方程;
(2)若方程有两个实数根,,且,求k的值.
20.如图,矩形中,的角平分线交于点E,F是延长线上一点,满足,连接,.
(1)求证:;
(2)当时,求的值.
21.如图,三个顶点的坐标分别为
(1)请画出绕点O旋转的图形;
(2)在x轴上找一点P,使的值最小,请直接写出点P的坐标.
22.某工厂生产一种产品,经市场调查发现,该产品每月的销售量y(件)与售价x(万元/件)之间满足一次函数关系,部分数据如表:
每件售价x/万元 … 24 26 28 30 32 …
月销售量y/件 … 52 48 44 40 36 …
该产品今年三月份的售价为35万元/件,利润为450万元.
(1)求:三月份每件产品的成本是多少万元?
(2)四月份工厂为了降低成本,提高产品质量,投资了450万元改进设备和革新技术,使每件产品的成本比三月份下降了14万元.若四月份每件产品的售价至少为25万元,且不高于30万元,求这个月获得的利润w(万元)关于售价x(万元/件)的函数关系式,并求最少利润是多少万元.
23.在平面直角坐标系中,若关于的函数的图像记为,将的图像绕着原点旋转得到图像,我们把和合起来的总图像称为 的“青一对称”图像.
(1)若在 的“青一对称”图像上,则 ;
(2)若在 的“青一对称”图像上,求的值;
(3)当二次函数的“青一对称”图像与直线有且只有三个交点时,请求出的值或取值范围.
24.如图,已知抛物线经过两点,直线是抛物线的对称轴.
(1)求抛物线的函数解析式及顶点的坐标;
(2)设点是直线上的一个动点,当时,求点的坐标;
(3)已知与抛物线相交于点,连接,若,求的值.
25.定义:函数图象上的点的纵坐标与横坐标的差叫做点的“双减差”,图象上所有点的“双减差”中最小值称为函数图象的“幸福值”如:抛物线上有点,则点的“双减差”为12;而抛物线上所有点的“双减差”,即该抛物线的“幸福值”为.根据定义,解答下列问题:
(1)已知函数图象上点的横坐标,求点的“双减差”的值;
(2)若直线的“幸福值”为,求的值;
(3)设抛物线顶点的横坐标为,且该抛物线的顶点在直线上,当时,抛物线的“幸福值”是5,求该抛物线的解析式.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 A A B D A A A B C A
二、填空题
11.【解】解:设小路的宽为,则长方形花坛的长为,宽为,
由题意得,,
同理得,
解得或(舍去),
∴小路的宽为,
故答案为:.
12.【解】解:点关于原点对称点的坐标是.
故答案为:.
13.【解】解:∵关于x的一元二次方程(k-1)x2-2x+1=0有两个不相等的实数根,
∴k-1≠0且 =(-2)2-4(k-1)>0,
解得:k<2且k≠1.
故答案为:k<2且k≠1.
14.【解】解:∵常数项为0,
∴,
解得:或2,
又∵,即,
∴.
15.【解】解:∵是绕点O顺时针旋转后得到的图形,
∴,,
∴,
∴,
故答案为:.
16.【解】解:在中,,,
故,
由旋转的性质可知:,,
∴,
在中,,,
故.
故答案为:.
三、解答题
17.【解】(1)由于A(﹣1,0)在一次函数y1=﹣x+m的图象上,得:
﹣(﹣1)+m=0,即m=﹣1;
已知A(﹣1,0)、B(2,﹣3)在二次函数y2=ax2+bx﹣3的图象上,则有:
,解得
∴二次函数的解析式为y2=x2﹣2x﹣3;
(2)由两个函数的图象知:当y1>y2时,﹣1<x<2.
18.【解】(1)解:依题意,得,
解得.
∴a的值为3.
(2)解:把代入原方程,得,
,
,
解得,.
19.【解】(1)解:当时,方程化为,
配方得,
∴,
解得,.
(2)解:,
方程总有实数根,
又,
或,
当时,,解得;
当时,则,解得;
或0.
20.【解】(1)证明:矩形中,,,,
平分,
,又,
,又,
,即,
又,,
,
;
(2)解:,且,
为等边三角形,
,设,,
则,,
,整理得,
故,开方得,又,
,
.
21.【解】(1)解: 如图所示,即为所求;
(2)解:作A点关于x轴的对称点,连接交x轴于点P,点P即为所求,
∴P点坐标为.
22.【解】(1)解:设y与x的函数关系式为,将,代入,得:
,
解得,
∴y与x的函数关系式为;
将代入,得(件),
设三月份每件产品的成本是a万元,
由题意得,
解得,
即三月份每件产品的成本是20万元;
(2)解:四月份每件产品的成本比三月份下降了14万元,则此时的成本为,
由题意得:
,
则抛物线的对称轴为,且,开口向下,
则时,取得最小值,
此时,,
即四月份最少利润是500万元.
23.【解】(1)解:由题意得:图像的函数解析式为,
当时,,
,
故答案为:;
(2)解:,
顶点坐标为,
图像的顶点坐标为,
的解析式为,
在 的“青一对称”图像上,
当时,,
解得:或(舍去),
当时,,
解得:或,
的值为或或;
(3)解:,
顶点坐标为,
将的图像绕着原点旋转得到图像,
的顶点坐标为,
的解析式为,
①当直线与:相切时,即直线与的图像只有一个交点,则,
整理得:,
,
解得:,
此时的解析式为:,
联立直线与的解析式得:,
整理得:,
此时,
直线与的图像只有两个交点,
当时,二次函数的“青一对称”图像与直线有且只有三个交点;
②当时, 的解析式为,的解析式为,
联立直线与的解析式得:,
解得:或(不合题意,舍去),
此时直线与的图像只有一个交点,
联立直线与的解析式得:,
解得:或,
当时,的图像与直线有两个交点和,
当时,二次函数的“青一对称”图像与直线只有三个交点;
当时,的解析式为,的解析式为,
联立直线与的解析式得:,
解得:或,
此时直线与的图像只有两个交点和,
联立直线与的解析式得:,
解得:或,
此时直线与的图像只有两个交点和,,
当时,二次函数的“青一对称”图像与直线有四个交点;
当时,二次函数的“青一对称”图像与直线有且只有三个交点;
综上所述,的值或取值范围是或.
24.【解】(1)解:把代入,得,
解得,
抛物线的函数解析式为,
,
顶点的坐标为;
(2)解:设,则,
当时,,
解得,
;
(3)解:延长交轴于,
设,在中,,
即,
解得,
,
设直线的解析式为,
代入,得,
解得,
的解析式为,
联立,
解得(舍去),,
,
.
25.【解】(1)解:将代入得:,
∴
∴点的“双减差”的值为:
(2)解:由得:,
∵,
∴,
∴随的增大而增大.
故:当时,有最小值,且最小值为:,
∴,
解得:(舍去)
∴
(3)解:由题意得:抛物线的顶点坐标为:,
∴
∴
令,则其对称轴为直线;
∵,
∴,即:;
,此时(不符合题意);
,即:,
此时,当,取最小值,
则,
解得:(舍去),
∴;
,即:,
此时,当,取最小值,
则,
解得:(舍去),
综上所述,该抛物线的解析式为:;
21世纪教育网(www.21cnjy.com)
同课章节目录
