22.3 实际问题与二次函数 同步练习 (含答案)2025-2026学年人教版数学九年级上册
文档属性
| 名称 | 22.3 实际问题与二次函数 同步练习 (含答案)2025-2026学年人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 408.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 12:32:05 | ||
图片预览

文档简介
22.3实际问题与二次函数 同步练习 2025-2026学年人教版数学九年级上册
一、单选题
1.共享单车为市民出行带来了方便,某单车公司第一个月投放辆单车,计划第三个月投放单车辆,如果第二个月的增长率是,第三个月的增长率是第二个月的2倍,那么与的函数关系是( )
A. B.
C. D.
2.某商店经营一种商品,在销售过程中,发现一周利润y(元)与每件销售价x(元)之间的关系满足,由于某种原因,价格只能,那么一周可获得最大利润是( )
A.1554 B.1556 C.1558 D.1560
3.如图,隧道的截面由抛物线和长方形构成.按照图中所示的平面直角坐标系,拋物线可以用表示.在抛物线型拱壁上需要安装两排灯,如果灯离地面的高度为.那么两排灯的水平距离是( )
A. B. C. D.
4.运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线可以看作是一条抛物线,不考虑空气阻力,足球距离地面的高度(单位:)与足球被踢出后经过的时间(单位:)近似满足函数关系.如图记录了3个时刻的数据,根据函数模型和所给数据,可推断出足球飞行到最高点时,最接近的时刻是( )
A.4 B.4.5 C.5 D.6
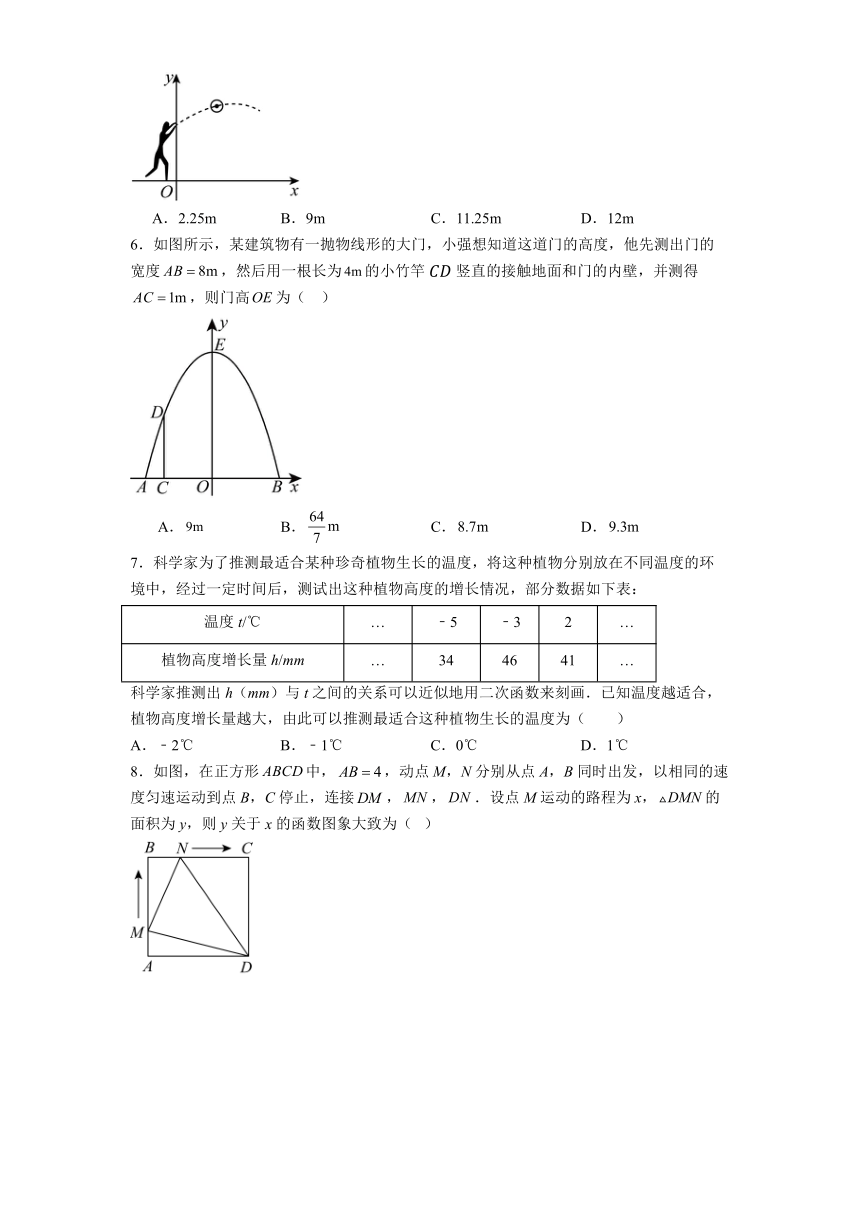
5.如图,一名运动员在水平地面上训练抛实心球,若以实心球出手时的正下方地面上一点O为原点建立平面直角坐标系,该运动员某次抛出去的实心球行进过程中的高度y(单位:m)与水平距离x(单位:m)之间的关系为,则该运动员这次抛出的水平距离为( )
A.2.25m B.9m C.11.25m D.12m
6.如图所示,某建筑物有一抛物线形的大门,小强想知道这道门的高度,他先测出门的宽度,然后用一根长为的小竹竿竖直的接触地面和门的内壁,并测得,则门高为( )
A. B. C. D.
7.科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况,部分数据如下表:
温度t/℃ … ﹣5 ﹣3 2 …
植物高度增长量h/mm … 34 46 41 …
科学家推测出h(mm)与t之间的关系可以近似地用二次函数来刻画.已知温度越适合,植物高度增长量越大,由此可以推测最适合这种植物生长的温度为( )
A.﹣2℃ B.﹣1℃ C.0℃ D.1℃
8.如图,在正方形中,,动点M,N分别从点A,B同时出发,以相同的速度匀速运动到点B,C停止,连接,,.设点M运动的路程为x,的面积为y,则y关于x的函数图象大致为( )
A. B.
C. D.
二、填空题
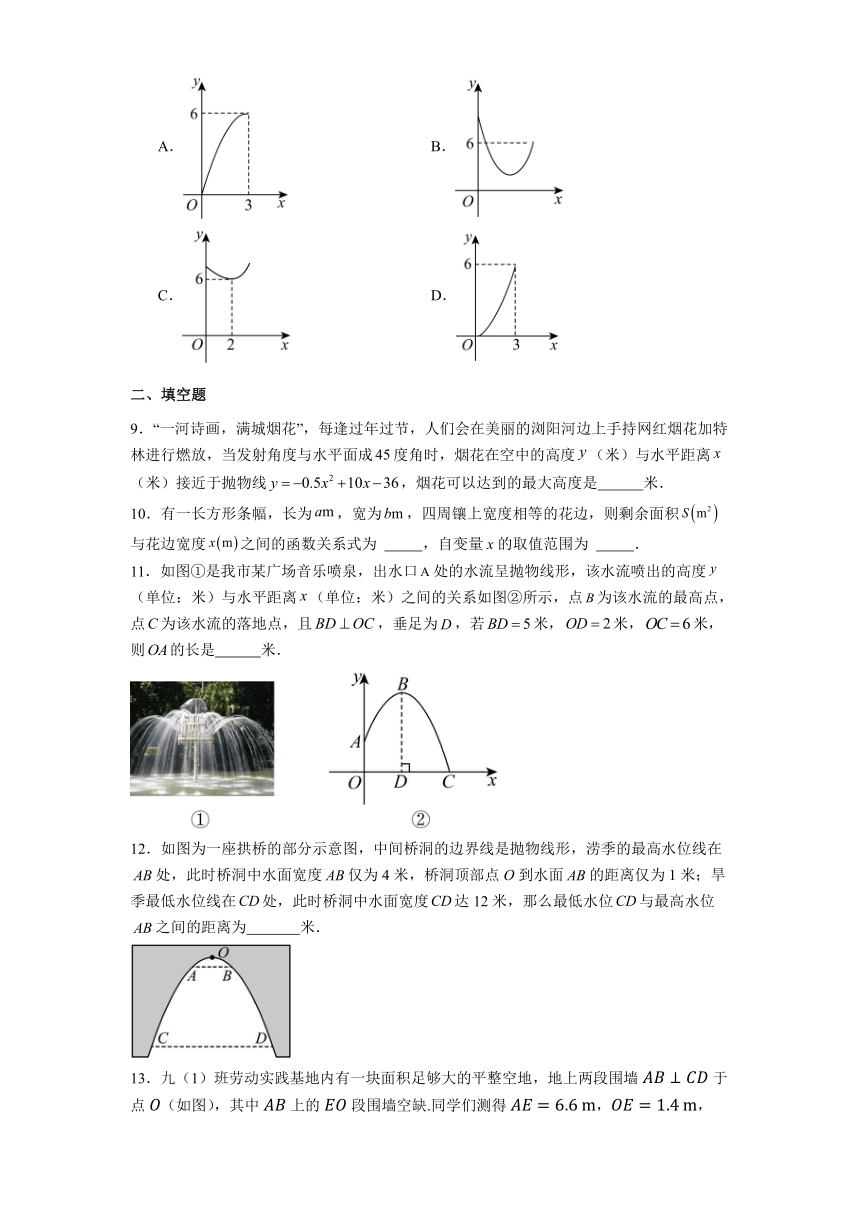
9.“一河诗画,满城烟花”,每逢过年过节,人们会在美丽的浏阳河边上手持网红烟花加特林进行燃放,当发射角度与水平面成度角时,烟花在空中的高度(米)与水平距离(米)接近于抛物线,烟花可以达到的最大高度是 米.
10.有一长方形条幅,长为,宽为,四周镶上宽度相等的花边,则剩余面积与花边宽度之间的函数关系式为 ,自变量x的取值范围为 .
11.如图①是我市某广场音乐喷泉,出水口处的水流呈抛物线形,该水流喷出的高度(单位:米)与水平距离(单位:米)之间的关系如图②所示,点为该水流的最高点,点为该水流的落地点,且,垂足为,若米,米,米,则的长是 米.
12.如图为一座拱桥的部分示意图,中间桥洞的边界线是抛物线形,涝季的最高水位线在处,此时桥洞中水面宽度仅为4米,桥洞顶部点O到水面的距离仅为1米;旱季最低水位线在处,此时桥洞中水面宽度达12米,那么最低水位与最高水位之间的距离为 米.
13.九(1)班劳动实践基地内有一块面积足够大的平整空地,地上两段围墙于点(如图),其中上的段围墙空缺.同学们测得,,,,,班长买来可切断的围栏,准备利用已有围墙,围出一块封闭的矩形菜地,则该菜地最大面积是____.
14.某超市购进一批拼装玩具,进价为每个10元,在销售过程中发现,日销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系,则该超市每天销售这款拼装玩具的最大利润为 元(利润=总销售额-总成本).
三、解答题
15.为了节省材料,某公司利用岸堤(岸堤足够长)为一边,用总长为80米的材料围成一个由三块面积相等的小矩形组成的矩形区域,如图为两个不同的方案.
(1)如图(1),若米,求矩形的面积(用含的代数式表示);
(2)如图(2),
①与的数量关系是 ;
②若米,求矩形的面积(用含的代数式表示),并求的最大值.
16.有一辆宽为的货车(如图(1)),要通过一条抛物线形隧道(如图(2)).为确保车辆安全通行,规定货车车顶左右两侧离隧道内壁的垂直高度至少为.已知隧道的跨度为,拱高为.
图(1) 图(2)
(1)若隧道为单车道,货车高为,该货车能否安全通行?为什么?
(2)若隧道为双车道,且两车道之间有的隔离带,通过计算说明该货车能够通行的最大安全高度.
17.嘉嘉和淇淇在玩沙包游戏.某同学借此情境编制了一道数学题,请解答这道题.
如图,在平面直角坐标系中,一个单位长度代表1 m长.嘉嘉在点A(6,1)处将沙包(看成点)抛出,其运动路线为抛物线C1:y=a(x-3)2+2 的一部分,淇淇恰在点B(0,c)处接住,然后跳起将沙包回传,其运动路线为抛物线C2:y=-x2+x+c+1的一部分.
(1)写出C1的最高点坐标,并求a,c的值.
(2)若嘉嘉在x轴上方1 m的高度上,且到点A水平距离不超过1 m的范围内可以接到沙包,求符合条件的n的整数值.
18.杭州第19届亚运会吉祥物组合名为“江南忆”,三个吉祥物以机器人作为整体造型,融合了杭州的历史人文、自然生态和创新基因,既有深厚的文化底蕴又充满了时代活力.某商家购进了A,B两种类型的吉祥物纪念品,已知每套A型纪念品比每套B型纪念品的进价多20元,1套A型纪念品与2套B型纪念品共200元.
(1)求A,B两种类型纪念品的进价;
(2)该商家准备购进A型纪念品套,均以每套元的价格全部售完,且与之间的关系满足一次函数,物价局规定该纪念品利润率不能高于,问的值为多少时,A型纪念品的销售总利润最大?最大利润是多少?
参考答案
1.A
2.B
3.D
4.B
5.B
6.B
7.B
8.C
9.
10. /
11.
12.8
13.46.4
14.800
15.,.由题意得, 矩形的面积为平方米.
① 根据题意知,,,,故答案为.
② 由题图(2)可知,.
,,,,,,, 当时,最大,最大值为300, 矩形的面积为平方米,最大值为300平方米.
16.货车能安全通行.理由如下:建立如图所示平面直角坐标系.
设抛物线的函数表达式为.将代入得,解得, 抛物线表达式为,当时,, 该货车能够安全通行.
(2) 时,, 货车能够通行的最大安全高度为.
17.(1)∵抛物线C1:y=a(x-3)2+2,∴C1的最高点坐标为(3,2).∵点A(6,1)在抛物线C1:y=a(x-3)2+2上,∴1=(6-3)2a+2,解得a=-,∴抛物线C1的解析式为y=-(x-3)2+2.令x=0,则c=-(0-3)2+2=1.
(2)∵嘉嘉在x轴上方1 m的高度上,且到点A水平距离不超过1 m的范围内可以接到沙包,∴可以接到沙包的位置的纵坐标为1,横坐标的取值范围为5≤x≤7.当抛物线C2经过(5,1)时,1=-×52+×5+1+1,解得n=;当抛物线C2经过(7,1)时,1=-×72+×7+1+1,解得n=,∴≤n≤,∴符合条件的n的整数值为4和5.
18.设A型纪念品的进价为元/套,B型纪念品的进价为元/套.
由题意得解得
答:A型纪念品的进价为80元/套,B型纪念品的进价为60元/套.
(2) 设A型纪念品的销售总利润为元.(元),的取值范围是.
根据题意得.
,, 当时,取最大值,最大值为,
故当的值为120时,A型纪念品的销售总利润最大,最大利润是1 200元.
第 page number 页,共 number of pages 页
一、单选题
1.共享单车为市民出行带来了方便,某单车公司第一个月投放辆单车,计划第三个月投放单车辆,如果第二个月的增长率是,第三个月的增长率是第二个月的2倍,那么与的函数关系是( )
A. B.
C. D.
2.某商店经营一种商品,在销售过程中,发现一周利润y(元)与每件销售价x(元)之间的关系满足,由于某种原因,价格只能,那么一周可获得最大利润是( )
A.1554 B.1556 C.1558 D.1560
3.如图,隧道的截面由抛物线和长方形构成.按照图中所示的平面直角坐标系,拋物线可以用表示.在抛物线型拱壁上需要安装两排灯,如果灯离地面的高度为.那么两排灯的水平距离是( )
A. B. C. D.
4.运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线可以看作是一条抛物线,不考虑空气阻力,足球距离地面的高度(单位:)与足球被踢出后经过的时间(单位:)近似满足函数关系.如图记录了3个时刻的数据,根据函数模型和所给数据,可推断出足球飞行到最高点时,最接近的时刻是( )
A.4 B.4.5 C.5 D.6
5.如图,一名运动员在水平地面上训练抛实心球,若以实心球出手时的正下方地面上一点O为原点建立平面直角坐标系,该运动员某次抛出去的实心球行进过程中的高度y(单位:m)与水平距离x(单位:m)之间的关系为,则该运动员这次抛出的水平距离为( )
A.2.25m B.9m C.11.25m D.12m
6.如图所示,某建筑物有一抛物线形的大门,小强想知道这道门的高度,他先测出门的宽度,然后用一根长为的小竹竿竖直的接触地面和门的内壁,并测得,则门高为( )
A. B. C. D.
7.科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况,部分数据如下表:
温度t/℃ … ﹣5 ﹣3 2 …
植物高度增长量h/mm … 34 46 41 …
科学家推测出h(mm)与t之间的关系可以近似地用二次函数来刻画.已知温度越适合,植物高度增长量越大,由此可以推测最适合这种植物生长的温度为( )
A.﹣2℃ B.﹣1℃ C.0℃ D.1℃
8.如图,在正方形中,,动点M,N分别从点A,B同时出发,以相同的速度匀速运动到点B,C停止,连接,,.设点M运动的路程为x,的面积为y,则y关于x的函数图象大致为( )
A. B.
C. D.
二、填空题
9.“一河诗画,满城烟花”,每逢过年过节,人们会在美丽的浏阳河边上手持网红烟花加特林进行燃放,当发射角度与水平面成度角时,烟花在空中的高度(米)与水平距离(米)接近于抛物线,烟花可以达到的最大高度是 米.
10.有一长方形条幅,长为,宽为,四周镶上宽度相等的花边,则剩余面积与花边宽度之间的函数关系式为 ,自变量x的取值范围为 .
11.如图①是我市某广场音乐喷泉,出水口处的水流呈抛物线形,该水流喷出的高度(单位:米)与水平距离(单位:米)之间的关系如图②所示,点为该水流的最高点,点为该水流的落地点,且,垂足为,若米,米,米,则的长是 米.
12.如图为一座拱桥的部分示意图,中间桥洞的边界线是抛物线形,涝季的最高水位线在处,此时桥洞中水面宽度仅为4米,桥洞顶部点O到水面的距离仅为1米;旱季最低水位线在处,此时桥洞中水面宽度达12米,那么最低水位与最高水位之间的距离为 米.
13.九(1)班劳动实践基地内有一块面积足够大的平整空地,地上两段围墙于点(如图),其中上的段围墙空缺.同学们测得,,,,,班长买来可切断的围栏,准备利用已有围墙,围出一块封闭的矩形菜地,则该菜地最大面积是____.
14.某超市购进一批拼装玩具,进价为每个10元,在销售过程中发现,日销售量y(个)与销售单价x(元)之间满足如图所示的一次函数关系,则该超市每天销售这款拼装玩具的最大利润为 元(利润=总销售额-总成本).
三、解答题
15.为了节省材料,某公司利用岸堤(岸堤足够长)为一边,用总长为80米的材料围成一个由三块面积相等的小矩形组成的矩形区域,如图为两个不同的方案.
(1)如图(1),若米,求矩形的面积(用含的代数式表示);
(2)如图(2),
①与的数量关系是 ;
②若米,求矩形的面积(用含的代数式表示),并求的最大值.
16.有一辆宽为的货车(如图(1)),要通过一条抛物线形隧道(如图(2)).为确保车辆安全通行,规定货车车顶左右两侧离隧道内壁的垂直高度至少为.已知隧道的跨度为,拱高为.
图(1) 图(2)
(1)若隧道为单车道,货车高为,该货车能否安全通行?为什么?
(2)若隧道为双车道,且两车道之间有的隔离带,通过计算说明该货车能够通行的最大安全高度.
17.嘉嘉和淇淇在玩沙包游戏.某同学借此情境编制了一道数学题,请解答这道题.
如图,在平面直角坐标系中,一个单位长度代表1 m长.嘉嘉在点A(6,1)处将沙包(看成点)抛出,其运动路线为抛物线C1:y=a(x-3)2+2 的一部分,淇淇恰在点B(0,c)处接住,然后跳起将沙包回传,其运动路线为抛物线C2:y=-x2+x+c+1的一部分.
(1)写出C1的最高点坐标,并求a,c的值.
(2)若嘉嘉在x轴上方1 m的高度上,且到点A水平距离不超过1 m的范围内可以接到沙包,求符合条件的n的整数值.
18.杭州第19届亚运会吉祥物组合名为“江南忆”,三个吉祥物以机器人作为整体造型,融合了杭州的历史人文、自然生态和创新基因,既有深厚的文化底蕴又充满了时代活力.某商家购进了A,B两种类型的吉祥物纪念品,已知每套A型纪念品比每套B型纪念品的进价多20元,1套A型纪念品与2套B型纪念品共200元.
(1)求A,B两种类型纪念品的进价;
(2)该商家准备购进A型纪念品套,均以每套元的价格全部售完,且与之间的关系满足一次函数,物价局规定该纪念品利润率不能高于,问的值为多少时,A型纪念品的销售总利润最大?最大利润是多少?
参考答案
1.A
2.B
3.D
4.B
5.B
6.B
7.B
8.C
9.
10. /
11.
12.8
13.46.4
14.800
15.,.由题意得, 矩形的面积为平方米.
① 根据题意知,,,,故答案为.
② 由题图(2)可知,.
,,,,,,, 当时,最大,最大值为300, 矩形的面积为平方米,最大值为300平方米.
16.货车能安全通行.理由如下:建立如图所示平面直角坐标系.
设抛物线的函数表达式为.将代入得,解得, 抛物线表达式为,当时,, 该货车能够安全通行.
(2) 时,, 货车能够通行的最大安全高度为.
17.(1)∵抛物线C1:y=a(x-3)2+2,∴C1的最高点坐标为(3,2).∵点A(6,1)在抛物线C1:y=a(x-3)2+2上,∴1=(6-3)2a+2,解得a=-,∴抛物线C1的解析式为y=-(x-3)2+2.令x=0,则c=-(0-3)2+2=1.
(2)∵嘉嘉在x轴上方1 m的高度上,且到点A水平距离不超过1 m的范围内可以接到沙包,∴可以接到沙包的位置的纵坐标为1,横坐标的取值范围为5≤x≤7.当抛物线C2经过(5,1)时,1=-×52+×5+1+1,解得n=;当抛物线C2经过(7,1)时,1=-×72+×7+1+1,解得n=,∴≤n≤,∴符合条件的n的整数值为4和5.
18.设A型纪念品的进价为元/套,B型纪念品的进价为元/套.
由题意得解得
答:A型纪念品的进价为80元/套,B型纪念品的进价为60元/套.
(2) 设A型纪念品的销售总利润为元.(元),的取值范围是.
根据题意得.
,, 当时,取最大值,最大值为,
故当的值为120时,A型纪念品的销售总利润最大,最大利润是1 200元.
第 page number 页,共 number of pages 页
同课章节目录
