3.4 一元一次方程的应用第3课时(共25张PPT)2025-2026学年数学湘教版(2024)七年级上册
文档属性
| 名称 | 3.4 一元一次方程的应用第3课时(共25张PPT)2025-2026学年数学湘教版(2024)七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
3.4 一元一次方程的应用
第3课时 方案问题和调配问题
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
空调是日常经常用到的家用电器,为我们的生活带来了极大的便利性,在选购的时候一定要重视.能效等级是衡量空调能效的重要指标之一,购买空调时要注意能效等级,选择能效等级低的空调可以更省电,但是能效等级低的空调一般价格也贵一些.
你能分析购买哪种空调综合费用较低吗?
壹
新知初探
贰
新知初探
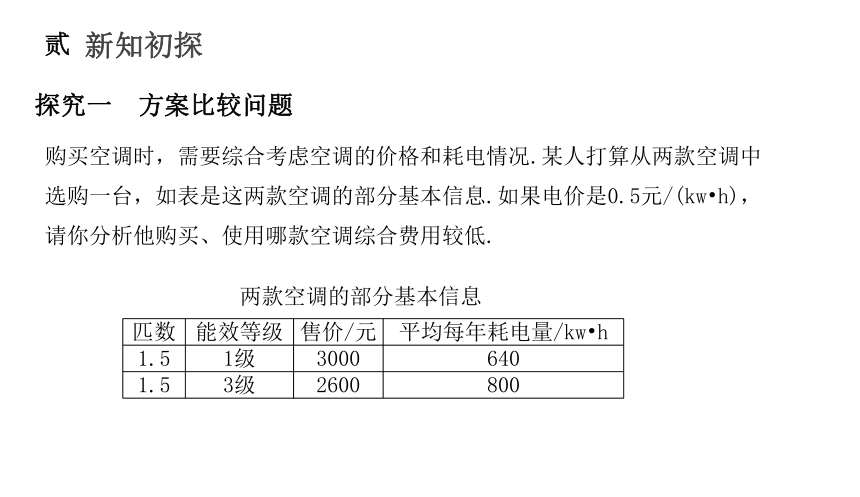
探究一 方案比较问题
购买空调时,需要综合考虑空调的价格和耗电情况.某人打算从两款空调中选购一台,如表是这两款空调的部分基本信息.如果电价是0.5元/(kw h),请你分析他购买、使用哪款空调综合费用较低.
两款空调的部分基本信息
匹数 能效等级 售价/元 平均每年耗电量/kw h
1.5 1级 3000 640
1.5 3级 2600 800
贰
选定一种空调后,售价是确定的,电费则与使用的时间有关.
设空调的使用年数是t,
则1级能效空调的综合费用(单位:元)是 .
3级能效空调的综合费用(单位:元)
是 .
3 000+320t
两款空调的部分基本信息
匹数 能效等级 售价/元 平均每年耗电量/kw h
1.5 1级 3000 640
1.5 3级 2600 800
购买空调时,需要综合考虑空调的价格和耗电情况.某人打算从两款空调中选购一台,如表是这两款空调的部分基本信息.如果电价是0.5元/(kw h),请你分析他购买、使用哪款空调综合费用较低.
问题1 在这个问题中,综合
费用= + .
空调的售价
电费
2 600+400t
解:列方程,得
3 000+320t=2 600+400t,
解得 t=5.
所以t取5时,两款空调的 综合费用相等.
两款空调的部分基本信息
匹数 能效等级 售价/元 平均每年耗电量/kw h
1.5 1级 3000 640
1.5 3级 2600 800
购买空调时,需要综合考虑空调的价格和耗电情况.某人打算从两款空调中选购一台,如表是这两款空调的部分基本信息.如果电价是0.5元/(kw h),请你分析他购买、使用哪款空调综合费用较低.
问题2 t取何值时,两款空调的综合费用相等?
问题3 t取何值时,哪款空调综合费用较低?
解:表示3级能效空调的综合费用的式子可变形为
2 600+400t
=3 000+320t+( )
=3 000+320t+80( ).
80t-400
t-5
当t<5时,80(t-5)是 数,这表明 级能效空调的综合费用较低;
当t>5时,80(t-5)是 数,这表明 级能效空调的综合费用较低;
负
3
正
1
由此可见,同样是1.5匹的空调,1级能效空调虽然售价高,但由于比较省电,使用年份长(超过5年)时综合费用反而低.根据相关行业标测空调的安全使用年限是10年(从生产日期计起),因此购买、使用1级能效空调更划算.
探究二 调配问题
3月12日植树节,为贯彻“绿水青山就是金山银山”的生态理念,学校组织植树活动.已知在甲处植树的有23人,在乙处植树的有17人.现调20人去支援,使在甲处植树的人数比乙处植树人数的2倍多3人,求应调往甲处的人数.
问题1 若设应调往甲处x人,根据题意填写表格.
调配前人数 调入人数 调配后人数
甲处 23 x
乙处 17
(20-x)
23+x
17+(20-x)
问题2 增派人数后甲处和乙处人数的数量关系是什么?可列出怎样的等式
答:增派人数后在甲处植树的人数比乙处植树人数的2倍多3人,
即23+x﹣2[17+(20﹣x)]=3.
问题3 你怎样就知道应调往甲处的人数?
解:设应调往甲处x人,则调往乙处(20﹣x)人,
根据题意得:23+x﹣2[17+(20﹣x)]=3,
解得:x=18.
答:应调往甲处18人.
探究三 例题讲解
例1 现有树苗若干棵,计划栽在一段公路的一侧,要求路的两端各栽1棵,并且相邻两棵树的间隔相等.
方案一:如果每隔5m栽1棵,则树苗缺21棵;
方案二:如果每隔5.5m栽1棵,则树苗正好用完.
根据以上方案,请算出原有树苗的棵数和这段路的长度.
分析观察植树示意图,想一想:
分析:
问题1 相邻两树的间隔长与应植树的棵数有什么关系?
答:相邻两树的间隔长的段数=植树棵数﹣1;
问题2 相邻两树的间隔长、应植树棵数与路长有怎样的数量关系?
答:路长=(植树棵数﹣1 )×间隔长.
方案 间隔/m 种植的树苗数 路长/m
一 5
二 5.5 x
问题3 设原有树苗x棵,填写下表:
问题4 两种方案下路长相等吗?根据路长关系列方程求解.
x+21
5(x+21-1)
5.5(x-1)
答:两种方案下路长是相等的.
解:设原有树苗x棵,根据题意,得,
5(x+21﹣1)=5.5(x﹣1),
解得:x=211,
因此,原有树苗211棵,这段公路长为
(211﹣1)×5.5=1155(米)
答:原有树苗211棵,这段路的长度为1155米.
例2 甲班有45人,乙班有39人.现在需要从甲、乙班各抽调一些同学去参加“歌唱祖国”歌咏比赛.如果从甲班抽调的人数比乙班多1人,那么甲班剩余人数恰好是乙班剩余人数的2倍.请问:从甲、乙两班各抽调了多少参加歌咏比赛?
分析:本题中有如下的等量关系:
(1)甲班抽调的人数-乙班抽调的人数=1;
(2)抽调之后甲班剩余人数=乙班剩余人数×2.
解:设从甲班抽调了x人,那么从乙班抽调了(x﹣1)人,
根据题意,得45﹣x=2[39﹣(x﹣1)],
解得:x=35,
于是x﹣1=35﹣1=34.
答:从甲班抽调了35人,从乙班抽调了34人参加歌咏比赛.
当堂达标
叁
当堂达标
1.某市对迎宾大道进行绿化,计划把某一段公路的一侧全部栽上桂花树,要求路的两端各栽一棵,并且每两棵树的间隔相等.如果每隔3米栽1棵,则树苗缺15棵;如果每隔4米栽1棵,则树苗缺1棵.则原有树苗的棵数是( )
A.41 B.42 C.43 D.44
2.某机械厂加工车间有33名工人,平均每名工人每天加工大齿轮5个或小齿轮15个,已知2个大齿轮和3个小齿轮配成一套,应安排 名工人加工大齿轮,才能刚好配套.
叁
B
22
4.某班打算买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售同样品牌的乒乓球和乒乓球拍,乒乓球拍每副定价30元,乒乓球每盒定价5元,经洽谈后,甲店买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠.该班需球拍5副,乒乓球若干盒(不小于5盒).问:
(1)当购买乒乓球15盒时,去哪家店购买比较优惠?
(2)当购买乒乓球多少盒时,两家店的付款一样多?
3.我国古代《孙子算经》记载了这样一个数学问题:“今有三人共车,二车空;二人共车,五人步.问车有几何?”意思是:每3人共乘一辆车,最终剩余2辆车;每2人共乘一辆车,最终有5人无车可乘,则车有 辆.
11
解:(1)甲:30×5+5×(15-5)=200(元)
乙:(30×5+5×15)×0.9=202.5(元)
因为200<202.5,
所以当购买乒乓球15盒时,去甲商店购买比较优惠,
答:当购买乒乓球15盒时,去甲商店购买比较优惠.
(2)设购买x 盒乒乓球时,两家店的付款一样多,根据题意得:
30×5+5(x-5)=(30×5+5x)×0.9,
解得:x=20,
答:当购买乒乓球20盒时,两家店的付款一样多.
课堂小结
肆
课堂小结
1.方案选择问题:方案选择问题可通过列方程或列式计算求解,再通过分类讨论或比较选择出最优方案.
2.调配问题:现实生活中,像“外部调配”“按比例调配”“内部调配”这样特殊的调配问题,由于其不同的调配等量关系页不相同,需要根据不同情况列出方程.
肆
课后作业
基础题:1.课后练习题 第 1,2题。
提高题:2.请学有余力的同学完成课后习题第7,8题
谢
谢
3.4 一元一次方程的应用
第3课时 方案问题和调配问题
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
空调是日常经常用到的家用电器,为我们的生活带来了极大的便利性,在选购的时候一定要重视.能效等级是衡量空调能效的重要指标之一,购买空调时要注意能效等级,选择能效等级低的空调可以更省电,但是能效等级低的空调一般价格也贵一些.
你能分析购买哪种空调综合费用较低吗?
壹
新知初探
贰
新知初探
探究一 方案比较问题
购买空调时,需要综合考虑空调的价格和耗电情况.某人打算从两款空调中选购一台,如表是这两款空调的部分基本信息.如果电价是0.5元/(kw h),请你分析他购买、使用哪款空调综合费用较低.
两款空调的部分基本信息
匹数 能效等级 售价/元 平均每年耗电量/kw h
1.5 1级 3000 640
1.5 3级 2600 800
贰
选定一种空调后,售价是确定的,电费则与使用的时间有关.
设空调的使用年数是t,
则1级能效空调的综合费用(单位:元)是 .
3级能效空调的综合费用(单位:元)
是 .
3 000+320t
两款空调的部分基本信息
匹数 能效等级 售价/元 平均每年耗电量/kw h
1.5 1级 3000 640
1.5 3级 2600 800
购买空调时,需要综合考虑空调的价格和耗电情况.某人打算从两款空调中选购一台,如表是这两款空调的部分基本信息.如果电价是0.5元/(kw h),请你分析他购买、使用哪款空调综合费用较低.
问题1 在这个问题中,综合
费用= + .
空调的售价
电费
2 600+400t
解:列方程,得
3 000+320t=2 600+400t,
解得 t=5.
所以t取5时,两款空调的 综合费用相等.
两款空调的部分基本信息
匹数 能效等级 售价/元 平均每年耗电量/kw h
1.5 1级 3000 640
1.5 3级 2600 800
购买空调时,需要综合考虑空调的价格和耗电情况.某人打算从两款空调中选购一台,如表是这两款空调的部分基本信息.如果电价是0.5元/(kw h),请你分析他购买、使用哪款空调综合费用较低.
问题2 t取何值时,两款空调的综合费用相等?
问题3 t取何值时,哪款空调综合费用较低?
解:表示3级能效空调的综合费用的式子可变形为
2 600+400t
=3 000+320t+( )
=3 000+320t+80( ).
80t-400
t-5
当t<5时,80(t-5)是 数,这表明 级能效空调的综合费用较低;
当t>5时,80(t-5)是 数,这表明 级能效空调的综合费用较低;
负
3
正
1
由此可见,同样是1.5匹的空调,1级能效空调虽然售价高,但由于比较省电,使用年份长(超过5年)时综合费用反而低.根据相关行业标测空调的安全使用年限是10年(从生产日期计起),因此购买、使用1级能效空调更划算.
探究二 调配问题
3月12日植树节,为贯彻“绿水青山就是金山银山”的生态理念,学校组织植树活动.已知在甲处植树的有23人,在乙处植树的有17人.现调20人去支援,使在甲处植树的人数比乙处植树人数的2倍多3人,求应调往甲处的人数.
问题1 若设应调往甲处x人,根据题意填写表格.
调配前人数 调入人数 调配后人数
甲处 23 x
乙处 17
(20-x)
23+x
17+(20-x)
问题2 增派人数后甲处和乙处人数的数量关系是什么?可列出怎样的等式
答:增派人数后在甲处植树的人数比乙处植树人数的2倍多3人,
即23+x﹣2[17+(20﹣x)]=3.
问题3 你怎样就知道应调往甲处的人数?
解:设应调往甲处x人,则调往乙处(20﹣x)人,
根据题意得:23+x﹣2[17+(20﹣x)]=3,
解得:x=18.
答:应调往甲处18人.
探究三 例题讲解
例1 现有树苗若干棵,计划栽在一段公路的一侧,要求路的两端各栽1棵,并且相邻两棵树的间隔相等.
方案一:如果每隔5m栽1棵,则树苗缺21棵;
方案二:如果每隔5.5m栽1棵,则树苗正好用完.
根据以上方案,请算出原有树苗的棵数和这段路的长度.
分析观察植树示意图,想一想:
分析:
问题1 相邻两树的间隔长与应植树的棵数有什么关系?
答:相邻两树的间隔长的段数=植树棵数﹣1;
问题2 相邻两树的间隔长、应植树棵数与路长有怎样的数量关系?
答:路长=(植树棵数﹣1 )×间隔长.
方案 间隔/m 种植的树苗数 路长/m
一 5
二 5.5 x
问题3 设原有树苗x棵,填写下表:
问题4 两种方案下路长相等吗?根据路长关系列方程求解.
x+21
5(x+21-1)
5.5(x-1)
答:两种方案下路长是相等的.
解:设原有树苗x棵,根据题意,得,
5(x+21﹣1)=5.5(x﹣1),
解得:x=211,
因此,原有树苗211棵,这段公路长为
(211﹣1)×5.5=1155(米)
答:原有树苗211棵,这段路的长度为1155米.
例2 甲班有45人,乙班有39人.现在需要从甲、乙班各抽调一些同学去参加“歌唱祖国”歌咏比赛.如果从甲班抽调的人数比乙班多1人,那么甲班剩余人数恰好是乙班剩余人数的2倍.请问:从甲、乙两班各抽调了多少参加歌咏比赛?
分析:本题中有如下的等量关系:
(1)甲班抽调的人数-乙班抽调的人数=1;
(2)抽调之后甲班剩余人数=乙班剩余人数×2.
解:设从甲班抽调了x人,那么从乙班抽调了(x﹣1)人,
根据题意,得45﹣x=2[39﹣(x﹣1)],
解得:x=35,
于是x﹣1=35﹣1=34.
答:从甲班抽调了35人,从乙班抽调了34人参加歌咏比赛.
当堂达标
叁
当堂达标
1.某市对迎宾大道进行绿化,计划把某一段公路的一侧全部栽上桂花树,要求路的两端各栽一棵,并且每两棵树的间隔相等.如果每隔3米栽1棵,则树苗缺15棵;如果每隔4米栽1棵,则树苗缺1棵.则原有树苗的棵数是( )
A.41 B.42 C.43 D.44
2.某机械厂加工车间有33名工人,平均每名工人每天加工大齿轮5个或小齿轮15个,已知2个大齿轮和3个小齿轮配成一套,应安排 名工人加工大齿轮,才能刚好配套.
叁
B
22
4.某班打算买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售同样品牌的乒乓球和乒乓球拍,乒乓球拍每副定价30元,乒乓球每盒定价5元,经洽谈后,甲店买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠.该班需球拍5副,乒乓球若干盒(不小于5盒).问:
(1)当购买乒乓球15盒时,去哪家店购买比较优惠?
(2)当购买乒乓球多少盒时,两家店的付款一样多?
3.我国古代《孙子算经》记载了这样一个数学问题:“今有三人共车,二车空;二人共车,五人步.问车有几何?”意思是:每3人共乘一辆车,最终剩余2辆车;每2人共乘一辆车,最终有5人无车可乘,则车有 辆.
11
解:(1)甲:30×5+5×(15-5)=200(元)
乙:(30×5+5×15)×0.9=202.5(元)
因为200<202.5,
所以当购买乒乓球15盒时,去甲商店购买比较优惠,
答:当购买乒乓球15盒时,去甲商店购买比较优惠.
(2)设购买x 盒乒乓球时,两家店的付款一样多,根据题意得:
30×5+5(x-5)=(30×5+5x)×0.9,
解得:x=20,
答:当购买乒乓球20盒时,两家店的付款一样多.
课堂小结
肆
课堂小结
1.方案选择问题:方案选择问题可通过列方程或列式计算求解,再通过分类讨论或比较选择出最优方案.
2.调配问题:现实生活中,像“外部调配”“按比例调配”“内部调配”这样特殊的调配问题,由于其不同的调配等量关系页不相同,需要根据不同情况列出方程.
肆
课后作业
基础题:1.课后练习题 第 1,2题。
提高题:2.请学有余力的同学完成课后习题第7,8题
谢
谢
同课章节目录
