4.3.1 角与角的大小比较(共32张PPT)2025-2026学年数学湘教版(2024)七年级上册
文档属性
| 名称 | 4.3.1 角与角的大小比较(共32张PPT)2025-2026学年数学湘教版(2024)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 16:36:47 | ||
图片预览









文档简介
(共32张PPT)
4.3 角
4.3.1 角与角的大小比较
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
观察左边的实物,你发现这些实物能抽象出什么样的共同形象?
——角
壹
新知初探
贰
新知初探
活动一 角的定义
观察与思考
问题1 观察以上角的图案,你能归纳出角的特点吗?尝试去描述一下角是由什么组成的图形?
贰
角的两边是由公共端点的两条射线组成的
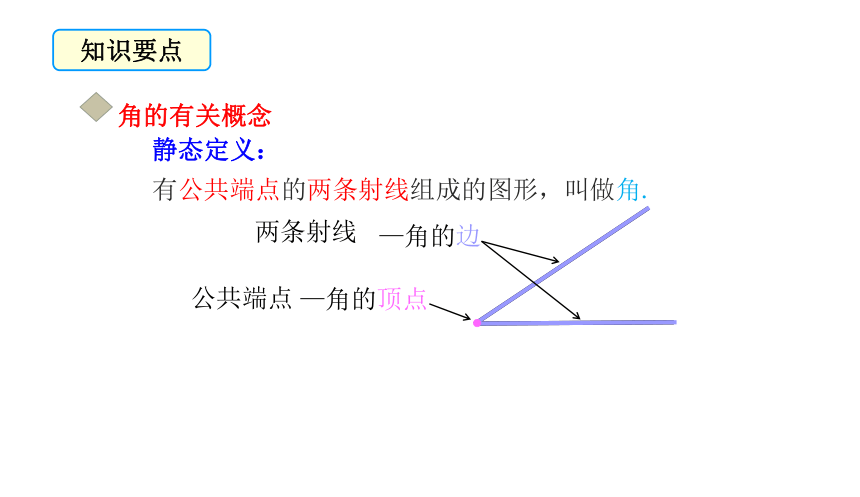
知识要点
静态定义:
有公共端点的两条射线组成的图形,叫做角.
公共端点
—角的顶点
两条射线
—角的边
角的有关概念
知识要点
角的有关概念
动态定义:角也可以看做由一条射线绕着它的端点旋转所形成的图形.
问题2 一条射线绕它的端点从一个位置旋转到另一位置时,形成的图形可以看作角吗?
答:可以看作角.射线的端点叫作角的顶点.射线原来所在的位置叫作角的始边,旋转后的位置叫作角的终边,统称角的边。从始边旋转到终边所扫过的区域,叫作角的内部。
始边
终边
O
A
B
(B)
平角
周角
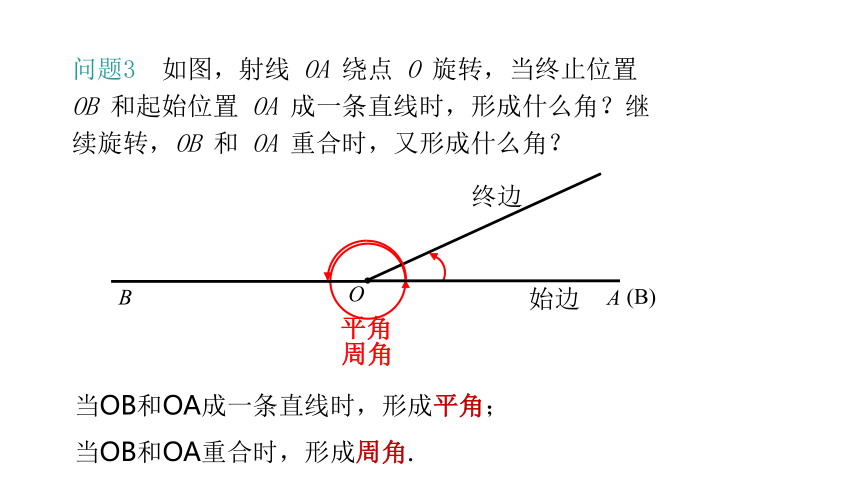
问题3 如图,射线 OA 绕点 O 旋转,当终止位置 OB 和起始位置 OA 成一条直线时,形成什么角?继续旋转,OB 和 OA 重合时,又形成什么角?
当OB和OA成一条直线时,形成平角;
当OB和OA重合时,形成周角.
(1)角的概念:有公共端点的两条射线组成的图形叫做角,
公共端点是角的顶点,两条射线是角的两条边.
(2)特殊的角:平角,周角.
归纳总结:
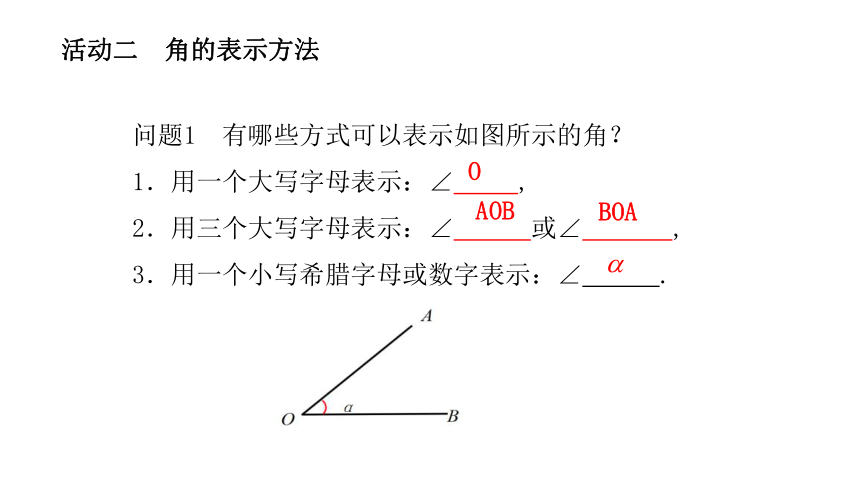
活动二 角的表示方法
问题1 有哪些方式可以表示如图所示的角?
1.用一个大写字母表示:∠ ,
2.用三个大写字母表示:∠ 或∠ ,
3.用一个小写希腊字母或数字表示:∠ .
O
AOB
BOA
问题2 下图中有哪些角?如何表示?还能用∠O表示∠AOB吗?
图中的角 、 、 ,
(填“能”或不能)用∠O表示∠AOB.
∠AOC(或∠1)
∠BOC(或∠α)
∠AOB
不能
要点归纳:
注意:
(1)当两个或两个以上的角共同一个顶点时,不能用一个大写字母表示;
(2)当用三个大写字母表示角时,必须把顶点字母放在中间;
(3)用数字或希腊字母表示角时,一定要在图形中用角弧标出.
角的表示方法:用一个大写字母表示,该大写字母表示的点为顶点;
用三个大写字母表示;用一个数字或一个小写希腊字母表示.
活动三 角的比较
问题1 如图,已知线段AB和线段CD,如何比较这两条线段的大小呢?
线段的大小可以用度量法和叠合法来比较.
(1)度量法
问题2 如图,已知∠ABC和∠DEF,类比线段的长短比较方法,你会比较角的大小吗?
A
B
C
D
E
F
2. 叠合法
A
B
O
(O' )
B'
(A' )
A
B
O
A
B
O
想一想:你能用图形和几何语言说明两个角的大小关系吗?( 两个角分别记作∠AOB,∠A'O'B' )
(O' )
B'
(A' )
∠AOB<∠A'O'B'
∠AOB =∠A'O'B'
∠AOB>∠A'O'B'
(O' )
(B' )
(A' )
3.张角比较法
如图设画出的两角分别为∠ABC,∠DEF.分别以两角的顶点B,E为圆心,以相同长度的半径画一段圆弧,与∠ABC,∠DEF的两边分别相交于点M,N及点P,Q,再将圆规尖移至点M处,使另一脚落在点N处.在不改变圆规张角的条件下,将圆规尖移至点P处.
如图 (1),若另一脚可与点Q重合,则∠ABC=∠DEF;
如图(2),若另一脚落在∠DEF内部,则∠ABC< ∠DEF;
如图(3),若另一脚落在∠DEF外部,则∠ABC>∠DEF.
活动四 角平分线
B
A
O
C
动手做一做:在纸上画∠AOB,然后将其剪下来,将其沿经过顶点的线对折,使边OA与OB重合.将角展开,折痕上任取一点记作点C.
类比线段中点的定义,填空:
∠AOC_____∠COB;
∠AOB=_____∠AOC.
=
2
【练习】
1.如图所示,写出图中符合下列条件的角.
(1)能用一个大写字母表示的角;
(2)以点A为顶点的角;
(3)所有小于180°的角.
解:(1)∠B,∠C.
(2)∠1(或∠CAD),∠2(或∠DAB),∠BAC.
(3)∠B,∠C,∠1,∠2,∠BAC,∠3,∠4.
2. 填写下表,将图中的角用不同方法表示出来.
∠1
∠3
∠4
∠ABC
∠ACB
∠BCE
∠5
∠BAC
∠BAD
∠2
2
1
3
4
5
B
A
D
C
E
2.(1)如图,射线OC、OD分别在∠AOB的内部、外部,下列各式错误的是( )
A.∠AOB<∠AOD B.∠BOC<∠AOB
C.∠COD<∠AOD D.∠AOB<∠AOC
(2)如图所示,其中最大的角是 ,∠DOC、∠DOB、∠DOA的大小关系是 .
D
∠AOD
∠DOA>∠DOB>∠DOC
3.在一张半透明的纸上通过折叠作出角的平分线.
解:(1)画图:在半透明纸上画出∠PQR;
(2)折纸:使∠PQR的两边QP和QR重合;
(3)展开:OH就是∠PQR的角平分线.
当堂达标
叁
当堂达标
1.下列说法正确的是( )
①平角就是直线;②角的大小与边的长短无关;③角的两边可以画一样长,也可以画一长一短;④角的两边是两条线段.
A.①② B.②③ C.②④ D.③④
2.下列说法中正确的是 ( )
A. 角的边可以一样长,也可以一长一短.B. 延长一个角的两边.
C. 反向延长射线OM得到一个平角 D. 周角是一条射线
B
C
叁
3.已知∠AOB,下列能说明射线OC是∠AOB的平分线的是 ( )
A. ∠AOB=2∠AOC B. ∠BOC=∠AOB
C. ∠AOC=∠BOC D. 以上都不对
4.∠α和∠β的顶点和一边都重合,另一边都在公共边的同侧,且∠α>∠β,那么∠α的另一边落在∠β的( )
A.另一边上 B.内部
C.外部 D.以上结论都不对
C
C
5.对于图中所表示的各个角,用“=”、“>”、“<”填空:
∠AOB ∠AOC,
∠BOC ∠DOB,
∠AOD ∠BOC,
∠AOD ∠DOA
<
<
>
=
5.如图所示:
A
B
C
4
3
2
1
O
(1) 图中共有多少个角?请写出能用一个字母表示的角;
答案:8个;∠A,∠O.
(2) 把图中所有的角都表示出来.
答案:∠A,∠O,∠1,∠2,∠3,∠4,∠ABC,∠ACB.
课堂小结
肆
课堂小结
1.角的概念:有公共端点的两条射线组成的图形
2.角的表示方法.
(1)三个大写字母或一个大写字母表示;
(2)一个数字表示;
(3)一个小写希腊字母表示.
3.角与角的大小比较
(1)度量法;(2)叠合法:(3)张角比较法
4.角的平分线的定义
肆
课后作业
基础题:1.课后练习 第 1,2,3题。
提高题:2.请学有余力的同学完成课后习题第1题
谢
谢
4.3 角
4.3.1 角与角的大小比较
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
观察左边的实物,你发现这些实物能抽象出什么样的共同形象?
——角
壹
新知初探
贰
新知初探
活动一 角的定义
观察与思考
问题1 观察以上角的图案,你能归纳出角的特点吗?尝试去描述一下角是由什么组成的图形?
贰
角的两边是由公共端点的两条射线组成的
知识要点
静态定义:
有公共端点的两条射线组成的图形,叫做角.
公共端点
—角的顶点
两条射线
—角的边
角的有关概念
知识要点
角的有关概念
动态定义:角也可以看做由一条射线绕着它的端点旋转所形成的图形.
问题2 一条射线绕它的端点从一个位置旋转到另一位置时,形成的图形可以看作角吗?
答:可以看作角.射线的端点叫作角的顶点.射线原来所在的位置叫作角的始边,旋转后的位置叫作角的终边,统称角的边。从始边旋转到终边所扫过的区域,叫作角的内部。
始边
终边
O
A
B
(B)
平角
周角
问题3 如图,射线 OA 绕点 O 旋转,当终止位置 OB 和起始位置 OA 成一条直线时,形成什么角?继续旋转,OB 和 OA 重合时,又形成什么角?
当OB和OA成一条直线时,形成平角;
当OB和OA重合时,形成周角.
(1)角的概念:有公共端点的两条射线组成的图形叫做角,
公共端点是角的顶点,两条射线是角的两条边.
(2)特殊的角:平角,周角.
归纳总结:
活动二 角的表示方法
问题1 有哪些方式可以表示如图所示的角?
1.用一个大写字母表示:∠ ,
2.用三个大写字母表示:∠ 或∠ ,
3.用一个小写希腊字母或数字表示:∠ .
O
AOB
BOA
问题2 下图中有哪些角?如何表示?还能用∠O表示∠AOB吗?
图中的角 、 、 ,
(填“能”或不能)用∠O表示∠AOB.
∠AOC(或∠1)
∠BOC(或∠α)
∠AOB
不能
要点归纳:
注意:
(1)当两个或两个以上的角共同一个顶点时,不能用一个大写字母表示;
(2)当用三个大写字母表示角时,必须把顶点字母放在中间;
(3)用数字或希腊字母表示角时,一定要在图形中用角弧标出.
角的表示方法:用一个大写字母表示,该大写字母表示的点为顶点;
用三个大写字母表示;用一个数字或一个小写希腊字母表示.
活动三 角的比较
问题1 如图,已知线段AB和线段CD,如何比较这两条线段的大小呢?
线段的大小可以用度量法和叠合法来比较.
(1)度量法
问题2 如图,已知∠ABC和∠DEF,类比线段的长短比较方法,你会比较角的大小吗?
A
B
C
D
E
F
2. 叠合法
A
B
O
(O' )
B'
(A' )
A
B
O
A
B
O
想一想:你能用图形和几何语言说明两个角的大小关系吗?( 两个角分别记作∠AOB,∠A'O'B' )
(O' )
B'
(A' )
∠AOB<∠A'O'B'
∠AOB =∠A'O'B'
∠AOB>∠A'O'B'
(O' )
(B' )
(A' )
3.张角比较法
如图设画出的两角分别为∠ABC,∠DEF.分别以两角的顶点B,E为圆心,以相同长度的半径画一段圆弧,与∠ABC,∠DEF的两边分别相交于点M,N及点P,Q,再将圆规尖移至点M处,使另一脚落在点N处.在不改变圆规张角的条件下,将圆规尖移至点P处.
如图 (1),若另一脚可与点Q重合,则∠ABC=∠DEF;
如图(2),若另一脚落在∠DEF内部,则∠ABC< ∠DEF;
如图(3),若另一脚落在∠DEF外部,则∠ABC>∠DEF.
活动四 角平分线
B
A
O
C
动手做一做:在纸上画∠AOB,然后将其剪下来,将其沿经过顶点的线对折,使边OA与OB重合.将角展开,折痕上任取一点记作点C.
类比线段中点的定义,填空:
∠AOC_____∠COB;
∠AOB=_____∠AOC.
=
2
【练习】
1.如图所示,写出图中符合下列条件的角.
(1)能用一个大写字母表示的角;
(2)以点A为顶点的角;
(3)所有小于180°的角.
解:(1)∠B,∠C.
(2)∠1(或∠CAD),∠2(或∠DAB),∠BAC.
(3)∠B,∠C,∠1,∠2,∠BAC,∠3,∠4.
2. 填写下表,将图中的角用不同方法表示出来.
∠1
∠3
∠4
∠ABC
∠ACB
∠BCE
∠5
∠BAC
∠BAD
∠2
2
1
3
4
5
B
A
D
C
E
2.(1)如图,射线OC、OD分别在∠AOB的内部、外部,下列各式错误的是( )
A.∠AOB<∠AOD B.∠BOC<∠AOB
C.∠COD<∠AOD D.∠AOB<∠AOC
(2)如图所示,其中最大的角是 ,∠DOC、∠DOB、∠DOA的大小关系是 .
D
∠AOD
∠DOA>∠DOB>∠DOC
3.在一张半透明的纸上通过折叠作出角的平分线.
解:(1)画图:在半透明纸上画出∠PQR;
(2)折纸:使∠PQR的两边QP和QR重合;
(3)展开:OH就是∠PQR的角平分线.
当堂达标
叁
当堂达标
1.下列说法正确的是( )
①平角就是直线;②角的大小与边的长短无关;③角的两边可以画一样长,也可以画一长一短;④角的两边是两条线段.
A.①② B.②③ C.②④ D.③④
2.下列说法中正确的是 ( )
A. 角的边可以一样长,也可以一长一短.B. 延长一个角的两边.
C. 反向延长射线OM得到一个平角 D. 周角是一条射线
B
C
叁
3.已知∠AOB,下列能说明射线OC是∠AOB的平分线的是 ( )
A. ∠AOB=2∠AOC B. ∠BOC=∠AOB
C. ∠AOC=∠BOC D. 以上都不对
4.∠α和∠β的顶点和一边都重合,另一边都在公共边的同侧,且∠α>∠β,那么∠α的另一边落在∠β的( )
A.另一边上 B.内部
C.外部 D.以上结论都不对
C
C
5.对于图中所表示的各个角,用“=”、“>”、“<”填空:
∠AOB ∠AOC,
∠BOC ∠DOB,
∠AOD ∠BOC,
∠AOD ∠DOA
<
<
>
=
5.如图所示:
A
B
C
4
3
2
1
O
(1) 图中共有多少个角?请写出能用一个字母表示的角;
答案:8个;∠A,∠O.
(2) 把图中所有的角都表示出来.
答案:∠A,∠O,∠1,∠2,∠3,∠4,∠ABC,∠ACB.
课堂小结
肆
课堂小结
1.角的概念:有公共端点的两条射线组成的图形
2.角的表示方法.
(1)三个大写字母或一个大写字母表示;
(2)一个数字表示;
(3)一个小写希腊字母表示.
3.角与角的大小比较
(1)度量法;(2)叠合法:(3)张角比较法
4.角的平分线的定义
肆
课后作业
基础题:1.课后练习 第 1,2,3题。
提高题:2.请学有余力的同学完成课后习题第1题
谢
谢
同课章节目录
