1.5.1 有理数的乘法(含2课时,共48张PPT)2025-2026学年数学湘教版(2024)七年级上册
文档属性
| 名称 | 1.5.1 有理数的乘法(含2课时,共48张PPT)2025-2026学年数学湘教版(2024)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 16:41:37 | ||
图片预览











文档简介
(共48张PPT)
1.5 有理数的乘法和除法
1.5.1 有理数的乘法
第1课时 有理数的乘法法则
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
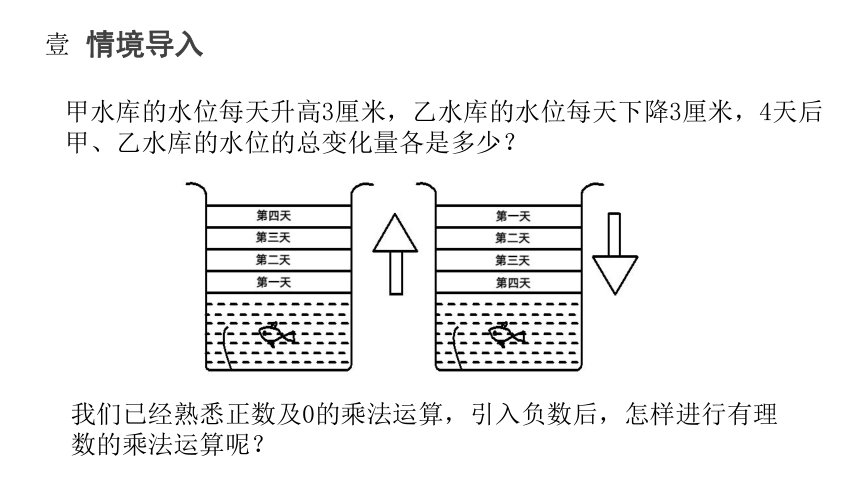
甲水库的水位每天升高3厘米,乙水库的水位每天下降3厘米,4天后
甲、乙水库的水位的总变化量各是多少?
我们已经熟悉正数及0的乘法运算,引入负数后,怎样进行有理数的乘法运算呢?
壹
新知初探
贰
探究一 有理数的乘法法则
新知初探
贰
(1)在运算过程中用了哪种运算律?
乘法对加法的分配律、
(2) 对于负有理数的乘法也适合这个乘法对加法的分配律吗
适合
(3) 3×(﹣5)应当规定为多少?你是怎么得到的?
3×(﹣5)=﹣(3×5)
小结:
正数与负数相乘得负数,并把绝对值相乘;0与负数相乘得0.
(5)(﹣5)×(﹣3)应当规定为多少?你是怎么得到的?
(﹣5)×(﹣3)=5×3.
小结:
负数与负数相乘得正数,并把绝对值相乘.
有理数乘法法则
1.同号两数相乘得正数,异号两数相乘得负数,并把绝对值相乘
2.任何数与0相乘,都得0.
问题1 设a,b为正有理数,c为任意有理数,则
(+a)×(+b)= ,(-a)×(-b)= ;
(-a)×(+b)= ,(+a)×(-b)= ;
c×0= ,0×c= .
思考:
0
a×b
a×b
-(a×b)
-(a×b)
0
问题2 (1)若a<0,b>0,则ab 0 ;
(2)若a<0,b<0,则ab 0 ;
(3)若ab>0,则a、b应满足什么条件?
(4)若ab<0,则a、b应满足什么条件?
<
>
a、b同号
a、b异号
两个有理数相乘,积是有理数吗
探究二 例题讲解
例1.确定乘积符号:
(1)5×(-11);(2)3×5;(3)(-2)×(-5);
(4)(-8)×0;(5)(﹣)×(-);(6)-2009×1;
有理数乘法积的符合确定:
(1)同号得正
(2)异号得负
解:(1)负;(2)正;(3)正;(4)0;(5)正;(6)负.
例2.计算:
(1)3×(-2) ; (2)( 8 )×5 ;
(3)0 ×(-6.18 ).
有理数乘法的求解步骤:
(1)先确定积的符号
(2)再确定积的绝对值
解:(1) 3×(-2)
=-(3×2)
=-6.
(2)(- 8 )×5
=﹣( 8 ×5)
=﹣40.
(3)0×(﹣6.18)
= 0 .
有理数乘法的求解步骤:
(1)先确定积的符号
(2)再确定积的绝对值
解:(4) (-)×0=0 .
(5)(- )×
=﹣( ×)
=﹣.
(6)(-)×(﹣)
= ×
=
(0)任何数与0相乘得0
3.用正负数表示气温的变化量,上升为正,下降为负.登山队攀登
一座山峰,每登高1km,气温的变化量为-6℃,攀登3km后,
气温有什么变化?
解:(-6)×3=-18
答:气温下降18℃.
当堂达标
叁
1.下列各式的计算结果中符号为正的是( )
A.(-5)×3 B.(+7)×(-6)
C.(-5)×0 D.(-5)×(-3.7)
2.下列说法中正确的有( )
①两数相乘,若积为正数,则这两个因数都是正数;
②两数相乘,若积为负数,则这两个数异号;
③两个数的积为0,则两个数都是0;
④互为相反数的数之积一定是负数.
(A)1个 (B)2个 (C)3个 (D)4个
当堂达标
D
A
叁
解:(1) (-3)×(-6)
=+(3×6)
=18.
3.计算:
(1)(-3)×(-6); (2)(- )× ;
(3)(-3.14)×0; (4)2 ×(- ).
(2)(- )×
=-( × )
=- .
(3)(-3.14)×0
=0.
(4)2 ×(- )
=-( × )
=- .
4.某冷库厂的一个冷库的室温是-1 ℃,现有一批食品需要低温
冷藏,如果冷库每小时可降温4 ℃,而连续降温6.5小时后,方可
达到所需冷藏温度,则这批食品需要冷藏的温度是多少 ℃
解:降温记作负.
(-4)×6.5=-26(℃)
所以(-1)+(-26)=-27(℃).
答:这批食品需要冷藏的温度是-27℃.
课堂小结
肆
课堂小结
1.有理数乘法法则:
(1)两数相乘,同号得正,异号得负,且积的绝对值等于乘数
的绝对值的积.
(2)任何数与0相乘,都得0.
2.乘积是1的两个数互为倒数
肆
课后作业
基础题:1.课后练习 第 1,2题。
提高题:2.若定义一种新的运算“*”,规定有理数a*b=4ab,
如2*3=4×2×3=24.
(1)求3*(-4)的值;
(2)求(-2)*(6*3)的值.
谢
谢
1.5有理数的乘法和除法
1.5.1 有理数的乘法
第2课时 有理数的乘法运算律
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
在小学里,我们都知道,数的乘法满足交换律、结合律和分配律,例如
3×5=5×3
(3×5)×2=3×(5×2)
3×(5+2)=3×5+3×2
学习了有理数后,这些运算律是否仍然适用呢?这就是这节课我们要研究的内容.
壹
新知初探
贰
新知初探
贰
问题1 阅读,并思考:
计算:(1)(﹣6)×[4+(-9)]= = ,
(﹣6)×4+(﹣6)×(-9)== = ,
(﹣6)×[4+(-9)] (﹣6)×4+(﹣6)×(-9).
(2)(﹣6)×[(-4)+9]= = ,
(﹣6)×(﹣4)+(﹣6)×9= = ,
(﹣6)×[(-4)+9] (﹣6)×(﹣4)+(﹣6)×9.
(-6)×(-5)
30
-24+54
30
=
(﹣6)×5
-30
24-54
-30
=
(3)(﹣6)×[(-4)+(-9)]= = ,
(﹣6)×(-4)+(﹣6)×(-9)== = ,
(﹣6)×[(-4)+(-9)] (﹣6)×(-4)+(﹣6)×(-9).
(-6)×(-13)
78
24+54
78
=
在上述运算过程中,你得到什么规律呢?
一个有理数与两个有理数的和相乘,等于把这个数分别与这两个数相乘,再把积相加.
分配律:
新知初探
(2)
(1)
问题2 计算下列各题.
贰
(﹣)×(-6)
(-6)×(﹣)
[(-2)×3]×(-4)
(-2)×[3×(-4)]
问题 比较它们的结果,你有什么发现?
乘法交换律:
一般地,有理数乘法中,两个数相乘,
交换乘数的位置,积不变.
(1)
乘数交换位置
a×b可以写成a b或ab,当用字母表示乘数时,“×” 可以写成“ ”或省略.
(-6)×(﹣)
1
(﹣)×(-6)
1
(3)
(4)
在有理数乘法中,三个数相乘,先把前两个数相乘,或者先把
后两个数相乘,积不变.
乘法结合律:
[(-2)×3]×(-4)
(-2)×[3×(-4)]
24
24
判断下列各式的积是正的还是负的?
2×3×4×(-5)
2×3×(-4)×(-5)
2×(-3)×(-4)×(-5)
(-2)×(-3)×(-4)×(-5)
7.8×(-8.1)×0×(-19.6)
负
正
负
正
零
问题:几个有理数相乘,因数都不为 0 时,积的符号怎样确定? 有一因数为 0 时,积是多少?
探究三 多个有理数的乘法法则
要点归纳:
几个不等于零的数相乘,
负的乘数的个数是 时,积为正数;
负的乘数的个数是 时,积为负数;
几个数相乘,如果其中有乘数为0,那么积为 .
偶数
奇数
}
奇负偶正
0
探究二 例题讲解
1. 计算:
(1)(﹣91)×(-);(2)(-85)×(-25)×(-4).
(2)(-85)×(-25)×(-4)
=(-85)×[(-25)×(-4)]
=(-85)×100
=-8500.
解:(1) (﹣91)×(-)
=(﹣91)×[(+(-)]
=(﹣91)×+(﹣91)×(-)
=﹣39+14
=﹣25
2.用两种方法计算:
解法一:
解法二:
【小结】
1.运用交换律时,在交换因数的位置时,要连同符号一起交换;
2.运用分配律时,要用括号外的因数乘括号内每一个因数,不能有遗漏;
3.三个以上的有理数相乘,可以任意交换因数的位置,或者把其中几个因数相乘.
4.括号外的因数是括号内所有分母的公倍数时,使用分配律.
例3 计算:
先确定积的符号
再确定积的绝对值
解:(1)
=-( )
=- .
(2)(-)×10×(-3.2 )×(-5)
=-(×10×3.2 ×5)
=-32.
当堂达标
叁
当堂达标
1.式子 中,运用的运算律是( )
A.乘法交换律及结合律B.乘法交换律及分配律
C.加法结合律及分配律D.乘法结合律及分配律
D
2.下列计算结果是负数的是( )
A.(-3)×4×(-5) B.(-3)×4×0
C.(-3)×4×(-5)×(-1) D.3×(-4)×(-5)
C
叁
4.计算:
(1)(-0.5)×20×(-0.8); (2)(-4)×(-6)×(-5).
解:(1)(-0.5)×20×(-0.8)
=0.5×20×0.8
=8.
3.在每一步算式的后面填上这一步所使用的运算律:
[(8×4)×125-5]×25
=[(4×8)×125-5]×25( )
=[4×(8×125)-5]×25( )
=4000×25-5×25( ).
乘法交换律
乘法结合律
乘法分配律
(2)(-4)×(-6)×(-5)
=-4×6×5
=-120.
5.运用运算律进行简便运算:
课堂小结
肆
课堂小结
1.有理数的乘法运算律:
(1)乘法交换律: ab=ba;
(2)乘法结合律: (ab)c=a(bc) ;
(3)乘法分配律: a(b+c)=ab+ac .
2.(1)多个有理数的乘法法则:
几个不是零的数相乘,负因数的个数为
(2)几个数相乘,若有因数为零,则积为零.
肆
课后作业
基础题:1.课后习题 第 1,2题。
提高题:2.请学有余力的同学完成课后习题第4,5题
谢
谢
1.5 有理数的乘法和除法
1.5.1 有理数的乘法
第1课时 有理数的乘法法则
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
甲水库的水位每天升高3厘米,乙水库的水位每天下降3厘米,4天后
甲、乙水库的水位的总变化量各是多少?
我们已经熟悉正数及0的乘法运算,引入负数后,怎样进行有理数的乘法运算呢?
壹
新知初探
贰
探究一 有理数的乘法法则
新知初探
贰
(1)在运算过程中用了哪种运算律?
乘法对加法的分配律、
(2) 对于负有理数的乘法也适合这个乘法对加法的分配律吗
适合
(3) 3×(﹣5)应当规定为多少?你是怎么得到的?
3×(﹣5)=﹣(3×5)
小结:
正数与负数相乘得负数,并把绝对值相乘;0与负数相乘得0.
(5)(﹣5)×(﹣3)应当规定为多少?你是怎么得到的?
(﹣5)×(﹣3)=5×3.
小结:
负数与负数相乘得正数,并把绝对值相乘.
有理数乘法法则
1.同号两数相乘得正数,异号两数相乘得负数,并把绝对值相乘
2.任何数与0相乘,都得0.
问题1 设a,b为正有理数,c为任意有理数,则
(+a)×(+b)= ,(-a)×(-b)= ;
(-a)×(+b)= ,(+a)×(-b)= ;
c×0= ,0×c= .
思考:
0
a×b
a×b
-(a×b)
-(a×b)
0
问题2 (1)若a<0,b>0,则ab 0 ;
(2)若a<0,b<0,则ab 0 ;
(3)若ab>0,则a、b应满足什么条件?
(4)若ab<0,则a、b应满足什么条件?
<
>
a、b同号
a、b异号
两个有理数相乘,积是有理数吗
探究二 例题讲解
例1.确定乘积符号:
(1)5×(-11);(2)3×5;(3)(-2)×(-5);
(4)(-8)×0;(5)(﹣)×(-);(6)-2009×1;
有理数乘法积的符合确定:
(1)同号得正
(2)异号得负
解:(1)负;(2)正;(3)正;(4)0;(5)正;(6)负.
例2.计算:
(1)3×(-2) ; (2)( 8 )×5 ;
(3)0 ×(-6.18 ).
有理数乘法的求解步骤:
(1)先确定积的符号
(2)再确定积的绝对值
解:(1) 3×(-2)
=-(3×2)
=-6.
(2)(- 8 )×5
=﹣( 8 ×5)
=﹣40.
(3)0×(﹣6.18)
= 0 .
有理数乘法的求解步骤:
(1)先确定积的符号
(2)再确定积的绝对值
解:(4) (-)×0=0 .
(5)(- )×
=﹣( ×)
=﹣.
(6)(-)×(﹣)
= ×
=
(0)任何数与0相乘得0
3.用正负数表示气温的变化量,上升为正,下降为负.登山队攀登
一座山峰,每登高1km,气温的变化量为-6℃,攀登3km后,
气温有什么变化?
解:(-6)×3=-18
答:气温下降18℃.
当堂达标
叁
1.下列各式的计算结果中符号为正的是( )
A.(-5)×3 B.(+7)×(-6)
C.(-5)×0 D.(-5)×(-3.7)
2.下列说法中正确的有( )
①两数相乘,若积为正数,则这两个因数都是正数;
②两数相乘,若积为负数,则这两个数异号;
③两个数的积为0,则两个数都是0;
④互为相反数的数之积一定是负数.
(A)1个 (B)2个 (C)3个 (D)4个
当堂达标
D
A
叁
解:(1) (-3)×(-6)
=+(3×6)
=18.
3.计算:
(1)(-3)×(-6); (2)(- )× ;
(3)(-3.14)×0; (4)2 ×(- ).
(2)(- )×
=-( × )
=- .
(3)(-3.14)×0
=0.
(4)2 ×(- )
=-( × )
=- .
4.某冷库厂的一个冷库的室温是-1 ℃,现有一批食品需要低温
冷藏,如果冷库每小时可降温4 ℃,而连续降温6.5小时后,方可
达到所需冷藏温度,则这批食品需要冷藏的温度是多少 ℃
解:降温记作负.
(-4)×6.5=-26(℃)
所以(-1)+(-26)=-27(℃).
答:这批食品需要冷藏的温度是-27℃.
课堂小结
肆
课堂小结
1.有理数乘法法则:
(1)两数相乘,同号得正,异号得负,且积的绝对值等于乘数
的绝对值的积.
(2)任何数与0相乘,都得0.
2.乘积是1的两个数互为倒数
肆
课后作业
基础题:1.课后练习 第 1,2题。
提高题:2.若定义一种新的运算“*”,规定有理数a*b=4ab,
如2*3=4×2×3=24.
(1)求3*(-4)的值;
(2)求(-2)*(6*3)的值.
谢
谢
1.5有理数的乘法和除法
1.5.1 有理数的乘法
第2课时 有理数的乘法运算律
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
在小学里,我们都知道,数的乘法满足交换律、结合律和分配律,例如
3×5=5×3
(3×5)×2=3×(5×2)
3×(5+2)=3×5+3×2
学习了有理数后,这些运算律是否仍然适用呢?这就是这节课我们要研究的内容.
壹
新知初探
贰
新知初探
贰
问题1 阅读,并思考:
计算:(1)(﹣6)×[4+(-9)]= = ,
(﹣6)×4+(﹣6)×(-9)== = ,
(﹣6)×[4+(-9)] (﹣6)×4+(﹣6)×(-9).
(2)(﹣6)×[(-4)+9]= = ,
(﹣6)×(﹣4)+(﹣6)×9= = ,
(﹣6)×[(-4)+9] (﹣6)×(﹣4)+(﹣6)×9.
(-6)×(-5)
30
-24+54
30
=
(﹣6)×5
-30
24-54
-30
=
(3)(﹣6)×[(-4)+(-9)]= = ,
(﹣6)×(-4)+(﹣6)×(-9)== = ,
(﹣6)×[(-4)+(-9)] (﹣6)×(-4)+(﹣6)×(-9).
(-6)×(-13)
78
24+54
78
=
在上述运算过程中,你得到什么规律呢?
一个有理数与两个有理数的和相乘,等于把这个数分别与这两个数相乘,再把积相加.
分配律:
新知初探
(2)
(1)
问题2 计算下列各题.
贰
(﹣)×(-6)
(-6)×(﹣)
[(-2)×3]×(-4)
(-2)×[3×(-4)]
问题 比较它们的结果,你有什么发现?
乘法交换律:
一般地,有理数乘法中,两个数相乘,
交换乘数的位置,积不变.
(1)
乘数交换位置
a×b可以写成a b或ab,当用字母表示乘数时,“×” 可以写成“ ”或省略.
(-6)×(﹣)
1
(﹣)×(-6)
1
(3)
(4)
在有理数乘法中,三个数相乘,先把前两个数相乘,或者先把
后两个数相乘,积不变.
乘法结合律:
[(-2)×3]×(-4)
(-2)×[3×(-4)]
24
24
判断下列各式的积是正的还是负的?
2×3×4×(-5)
2×3×(-4)×(-5)
2×(-3)×(-4)×(-5)
(-2)×(-3)×(-4)×(-5)
7.8×(-8.1)×0×(-19.6)
负
正
负
正
零
问题:几个有理数相乘,因数都不为 0 时,积的符号怎样确定? 有一因数为 0 时,积是多少?
探究三 多个有理数的乘法法则
要点归纳:
几个不等于零的数相乘,
负的乘数的个数是 时,积为正数;
负的乘数的个数是 时,积为负数;
几个数相乘,如果其中有乘数为0,那么积为 .
偶数
奇数
}
奇负偶正
0
探究二 例题讲解
1. 计算:
(1)(﹣91)×(-);(2)(-85)×(-25)×(-4).
(2)(-85)×(-25)×(-4)
=(-85)×[(-25)×(-4)]
=(-85)×100
=-8500.
解:(1) (﹣91)×(-)
=(﹣91)×[(+(-)]
=(﹣91)×+(﹣91)×(-)
=﹣39+14
=﹣25
2.用两种方法计算:
解法一:
解法二:
【小结】
1.运用交换律时,在交换因数的位置时,要连同符号一起交换;
2.运用分配律时,要用括号外的因数乘括号内每一个因数,不能有遗漏;
3.三个以上的有理数相乘,可以任意交换因数的位置,或者把其中几个因数相乘.
4.括号外的因数是括号内所有分母的公倍数时,使用分配律.
例3 计算:
先确定积的符号
再确定积的绝对值
解:(1)
=-( )
=- .
(2)(-)×10×(-3.2 )×(-5)
=-(×10×3.2 ×5)
=-32.
当堂达标
叁
当堂达标
1.式子 中,运用的运算律是( )
A.乘法交换律及结合律B.乘法交换律及分配律
C.加法结合律及分配律D.乘法结合律及分配律
D
2.下列计算结果是负数的是( )
A.(-3)×4×(-5) B.(-3)×4×0
C.(-3)×4×(-5)×(-1) D.3×(-4)×(-5)
C
叁
4.计算:
(1)(-0.5)×20×(-0.8); (2)(-4)×(-6)×(-5).
解:(1)(-0.5)×20×(-0.8)
=0.5×20×0.8
=8.
3.在每一步算式的后面填上这一步所使用的运算律:
[(8×4)×125-5]×25
=[(4×8)×125-5]×25( )
=[4×(8×125)-5]×25( )
=4000×25-5×25( ).
乘法交换律
乘法结合律
乘法分配律
(2)(-4)×(-6)×(-5)
=-4×6×5
=-120.
5.运用运算律进行简便运算:
课堂小结
肆
课堂小结
1.有理数的乘法运算律:
(1)乘法交换律: ab=ba;
(2)乘法结合律: (ab)c=a(bc) ;
(3)乘法分配律: a(b+c)=ab+ac .
2.(1)多个有理数的乘法法则:
几个不是零的数相乘,负因数的个数为
(2)几个数相乘,若有因数为零,则积为零.
肆
课后作业
基础题:1.课后习题 第 1,2题。
提高题:2.请学有余力的同学完成课后习题第4,5题
谢
谢
同课章节目录
