1.5.3 有理数的乘除(共21张PPT)2025-2026学年数学湘教版(2024)七年级上册
文档属性
| 名称 | 1.5.3 有理数的乘除(共21张PPT)2025-2026学年数学湘教版(2024)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 16:42:30 | ||
图片预览






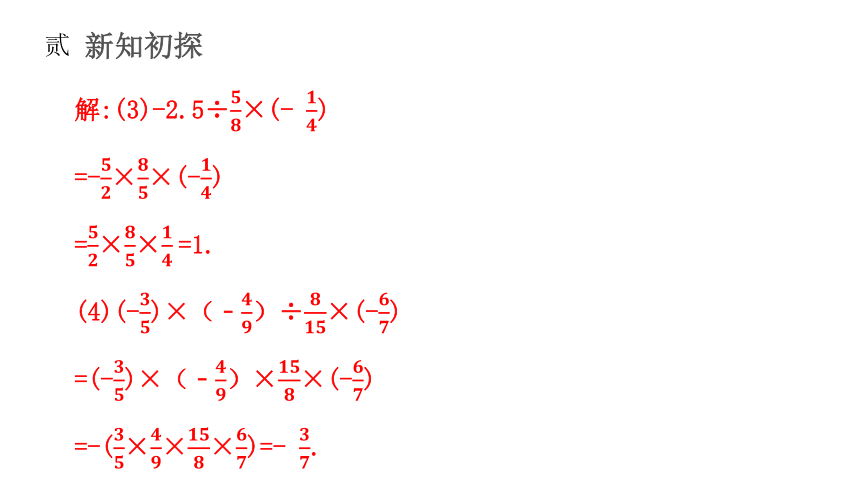

文档简介
(共21张PPT)
1.5 有理数的乘法和除法
1.5.3 有理数的乘除
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
问题1:小学的四则混合运算的顺序是怎样的?
先乘除,后加减,同级运算从左至右,有括号先算括号内,再算括号外.括号计算顺序:先小括号,再中括号,最后大括号.
问题2:我们目前都学习了哪些运算?
加法、减法、乘法、除法.
一个运算中,含有有理数的加、减、乘、除、等多种运算,称为有理数的混合运算.
壹
新知初探
贰
新知初探
活动一 有理数的乘除混合运算
贰
1.计算:
(1)(﹣10)÷[(﹣5)×(﹣2)];
(2)(﹣56)÷(﹣2)÷(﹣8);
(3)-2.5÷××(- );
(4)(- )×(﹣)÷×(- ).
新知初探
贰
解:(1)(﹣10)÷[(﹣5)×(﹣2)];
=(﹣10)÷10
=﹣1;
(2)(﹣56)÷(﹣2)÷(﹣8);
=28÷(﹣8)
=﹣;
新知初探
贰
解:(3)-2.5÷×(- )
=-××(-)
=××=1.
(4)(-)×(﹣)÷×(-)
=(-)×(﹣)××(-)
=-(×××)=- .
问题 观察上面的乘除混合运算,运算顺序是什么
你能得出什么结论
小结:
(1)乘除混合运算时,有括号的先计算括号内的运算.
(2)乘除混合运算往往先将除法化为乘法,然后确定积的符号,
最后求出结果(乘除混合运算按从左到右的顺序进行计算).
(3)有理数除法化为有理数乘法以后,可以利用有理数乘法
的运算律简化运算.
活动二 有理数的乘除混合运算的实际应用
2.(1)一辆汽车匀速行驶3小时行驶了240千米,以同样的速度,行驶5小时可以行驶多少千米?
(2)一种药瓶的包装上写着:90片,每片10克.医生开的处方上写着:每天吃3次,每次20克.这瓶药按医生的处方,可以吃多少天?
解:(1)240÷3×5=80×=440
答:可以行驶440千米.
(2)(10×90)÷(20×3)=900÷60=15(天),
答:可以吃15天.
1.计算器是一种方便实用的计算工具,用计算器进行比较复杂的数的计算比笔算要快捷得多.
2.提倡在明确算理的情况下,恰当地使用计算器进行一些比较复杂的有理数加减乘除法的混合运算.
当堂达标
叁
当堂达标
1.下列计算正确的是( )
A.-3.5÷ ×(- )=-3
B.-2÷3×3=-
C.(-6)÷(-4)÷(+ )=
D.
2.当a=-3,b=-2,c=5时,a÷|b|÷c的值为 .
C
叁
3.计算:
(3)(- )×(- )÷[(- )×].
(3)(-)×(- )÷[(-)×
=(﹣)×(﹣)÷(﹣)
=(﹣)×(﹣)×(﹣)
=﹣.
4.小明有5张写着不同数字的卡片,完成下列各问题:
﹣2.5,3,,﹣4,5.
(1)把卡片上的5个数在数轴上表示出来;
(2)从中取出3张卡片,将这3张卡片上的数字相乘,乘积的最大值为多少;
(3)从中取出2张卡片,将这2张卡片上的数字相除,商的最小值为多少.
(3)-4.325×(-0.012)-2.31÷(-5.315)≈0.49.
解:(1)将各数表示到数轴上如图所示:
;
(2)取出3张卡片,使这3张卡片上数的乘积最大,
当两负一正时:﹣2.5×(﹣4)×5=50,
当三个都是正数时:3×5× = ,
因为 <50 ,所以乘积的最大值为50;
(3)因为取出2张卡片,商的最小,
所以分别取所给数中正负数的最小值,即﹣4÷=﹣8.
课堂小结
肆
课堂小结
11.在只有有理数的乘法和除考运算时,如果没有括号,则按照从左到右的顺序依次计算,并可以把除法转化为乘法,然后再按照乘法法则进行计算;如果有括号,就先做括号内的运算.
2.进行有理数的乘除混合运算时应注意运用运算律进行简化计算.
肆
课后作业
基础题:1.课后练习 第1,2题。
提高题:2.请学有余力的同学完成课后习题第9题
谢
谢
1.5 有理数的乘法和除法
1.5.3 有理数的乘除
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
情境导入
问题1:小学的四则混合运算的顺序是怎样的?
先乘除,后加减,同级运算从左至右,有括号先算括号内,再算括号外.括号计算顺序:先小括号,再中括号,最后大括号.
问题2:我们目前都学习了哪些运算?
加法、减法、乘法、除法.
一个运算中,含有有理数的加、减、乘、除、等多种运算,称为有理数的混合运算.
壹
新知初探
贰
新知初探
活动一 有理数的乘除混合运算
贰
1.计算:
(1)(﹣10)÷[(﹣5)×(﹣2)];
(2)(﹣56)÷(﹣2)÷(﹣8);
(3)-2.5÷××(- );
(4)(- )×(﹣)÷×(- ).
新知初探
贰
解:(1)(﹣10)÷[(﹣5)×(﹣2)];
=(﹣10)÷10
=﹣1;
(2)(﹣56)÷(﹣2)÷(﹣8);
=28÷(﹣8)
=﹣;
新知初探
贰
解:(3)-2.5÷×(- )
=-××(-)
=××=1.
(4)(-)×(﹣)÷×(-)
=(-)×(﹣)××(-)
=-(×××)=- .
问题 观察上面的乘除混合运算,运算顺序是什么
你能得出什么结论
小结:
(1)乘除混合运算时,有括号的先计算括号内的运算.
(2)乘除混合运算往往先将除法化为乘法,然后确定积的符号,
最后求出结果(乘除混合运算按从左到右的顺序进行计算).
(3)有理数除法化为有理数乘法以后,可以利用有理数乘法
的运算律简化运算.
活动二 有理数的乘除混合运算的实际应用
2.(1)一辆汽车匀速行驶3小时行驶了240千米,以同样的速度,行驶5小时可以行驶多少千米?
(2)一种药瓶的包装上写着:90片,每片10克.医生开的处方上写着:每天吃3次,每次20克.这瓶药按医生的处方,可以吃多少天?
解:(1)240÷3×5=80×=440
答:可以行驶440千米.
(2)(10×90)÷(20×3)=900÷60=15(天),
答:可以吃15天.
1.计算器是一种方便实用的计算工具,用计算器进行比较复杂的数的计算比笔算要快捷得多.
2.提倡在明确算理的情况下,恰当地使用计算器进行一些比较复杂的有理数加减乘除法的混合运算.
当堂达标
叁
当堂达标
1.下列计算正确的是( )
A.-3.5÷ ×(- )=-3
B.-2÷3×3=-
C.(-6)÷(-4)÷(+ )=
D.
2.当a=-3,b=-2,c=5时,a÷|b|÷c的值为 .
C
叁
3.计算:
(3)(- )×(- )÷[(- )×].
(3)(-)×(- )÷[(-)×
=(﹣)×(﹣)÷(﹣)
=(﹣)×(﹣)×(﹣)
=﹣.
4.小明有5张写着不同数字的卡片,完成下列各问题:
﹣2.5,3,,﹣4,5.
(1)把卡片上的5个数在数轴上表示出来;
(2)从中取出3张卡片,将这3张卡片上的数字相乘,乘积的最大值为多少;
(3)从中取出2张卡片,将这2张卡片上的数字相除,商的最小值为多少.
(3)-4.325×(-0.012)-2.31÷(-5.315)≈0.49.
解:(1)将各数表示到数轴上如图所示:
;
(2)取出3张卡片,使这3张卡片上数的乘积最大,
当两负一正时:﹣2.5×(﹣4)×5=50,
当三个都是正数时:3×5× = ,
因为 <50 ,所以乘积的最大值为50;
(3)因为取出2张卡片,商的最小,
所以分别取所给数中正负数的最小值,即﹣4÷=﹣8.
课堂小结
肆
课堂小结
11.在只有有理数的乘法和除考运算时,如果没有括号,则按照从左到右的顺序依次计算,并可以把除法转化为乘法,然后再按照乘法法则进行计算;如果有括号,就先做括号内的运算.
2.进行有理数的乘除混合运算时应注意运用运算律进行简化计算.
肆
课后作业
基础题:1.课后练习 第1,2题。
提高题:2.请学有余力的同学完成课后习题第9题
谢
谢
同课章节目录
