九年级数学上册人教版第24.3节《正多边形和圆》课时练习题(含答案)
文档属性
| 名称 | 九年级数学上册人教版第24.3节《正多边形和圆》课时练习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 899.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 17:02:44 | ||
图片预览


文档简介
九年级数学上册人教版第24.3节《正多边形和圆》课时练习题
一、单选题
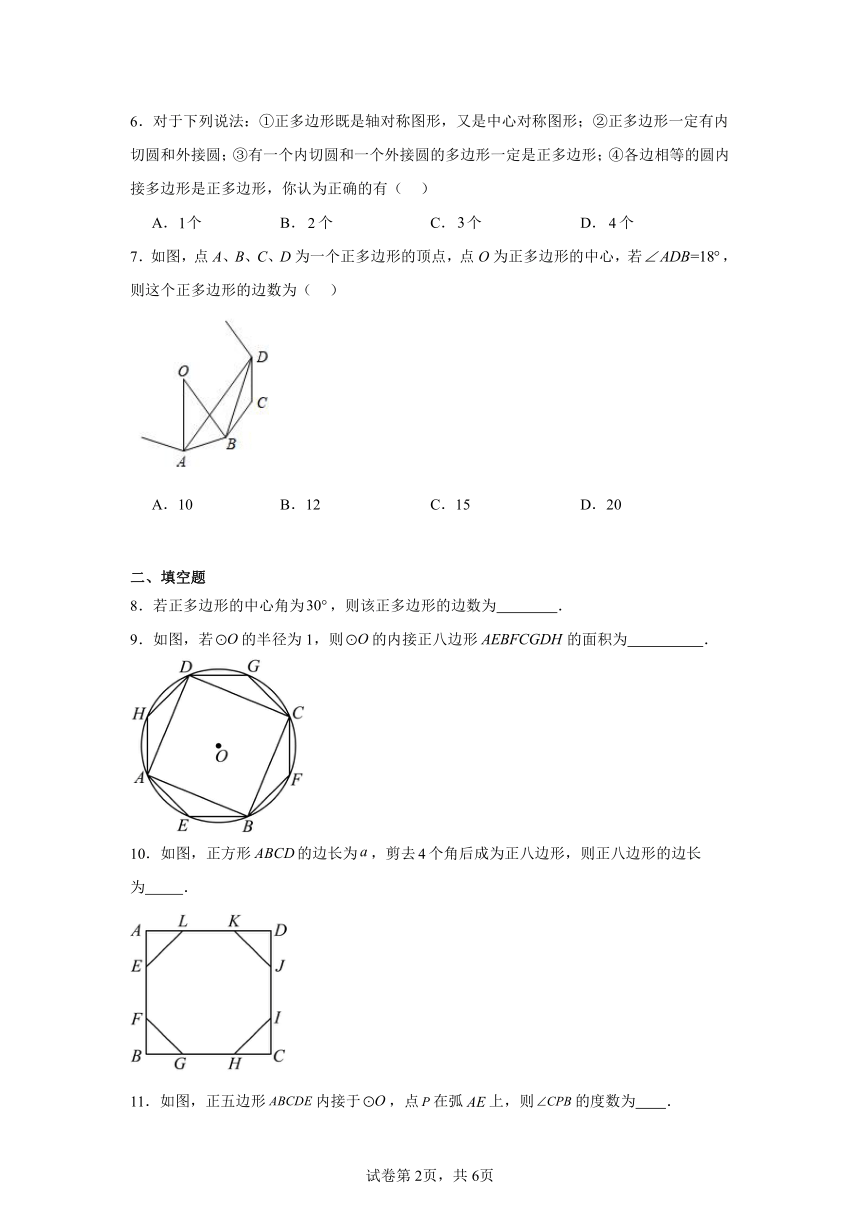
1.如图,以点为圆心的两个同心圆把以为半径的大圆的面积三等分,这两个圆的半径分别为,.则的值是( )
A. B. C. D.
2.若正多边形的一个外角为,则这个正多边形的中心角的度数是( )
A. B. C. D.
3.如图所示,某同学作了一个圆内接正十二边形.若的半径为1,则这个圆内接正十二边形的面积为( )
A.1 B.3 C. D.
4.同一个圆的内角正三角形、正方形、正六边形的边心距的比为( )
A. B. C. D.
5.如图,的半径为, ABC是的内接等边三角形,点在上.四边形为平行四边形,则平行四边形的面积是( )
A.4 B.4 C.2 D.2
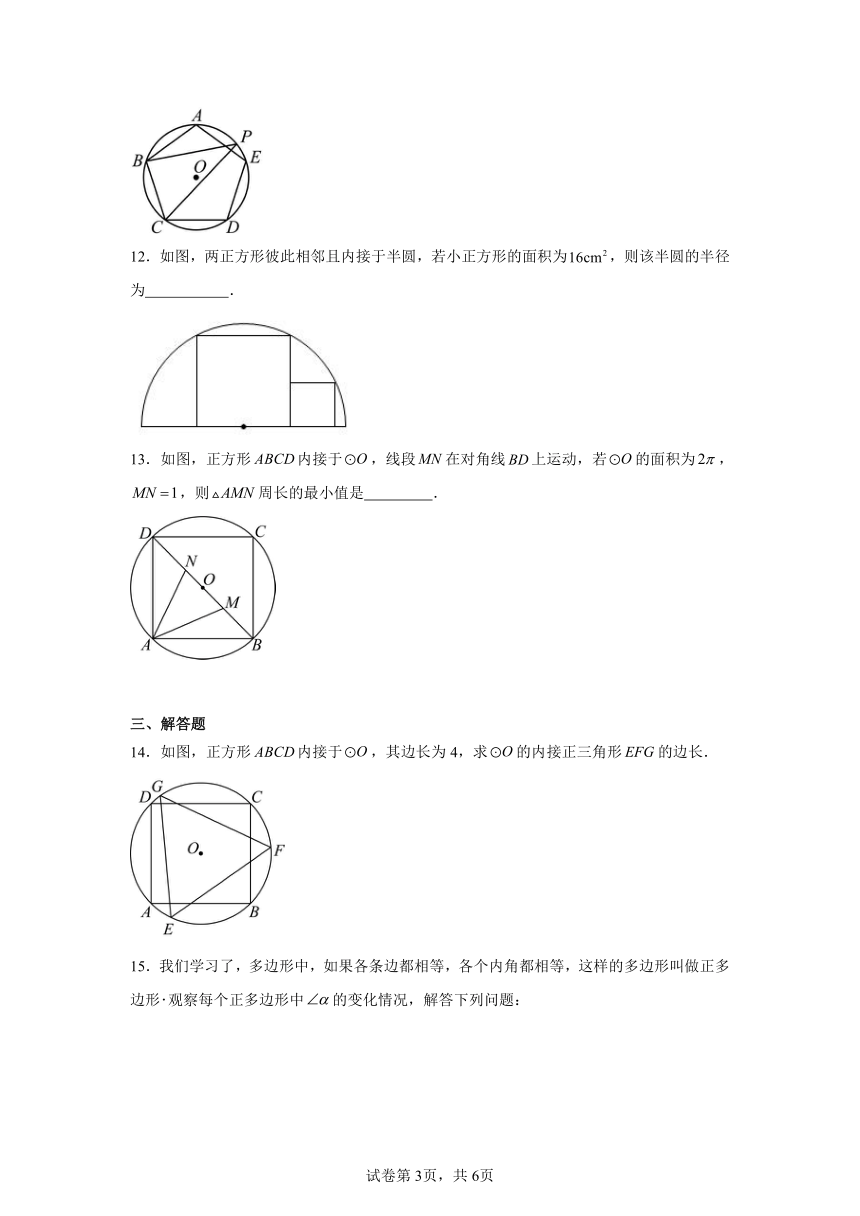
6.对于下列说法:①正多边形既是轴对称图形,又是中心对称图形;②正多边形一定有内切圆和外接圆;③有一个内切圆和一个外接圆的多边形一定是正多边形;④各边相等的圆内接多边形是正多边形,你认为正确的有( )
A.个 B.个 C.个 D.个
7.如图,点A、B、C、D为一个正多边形的顶点,点O为正多边形的中心,若,则这个正多边形的边数为( )
A.10 B.12 C.15 D.20
二、填空题
8.若正多边形的中心角为,则该正多边形的边数为 .
9.如图,若的半径为1,则的内接正八边形的面积为 .
10.如图,正方形的边长为,剪去个角后成为正八边形,则正八边形的边长为 .
11.如图,正五边形内接于,点在弧上,则的度数为 .
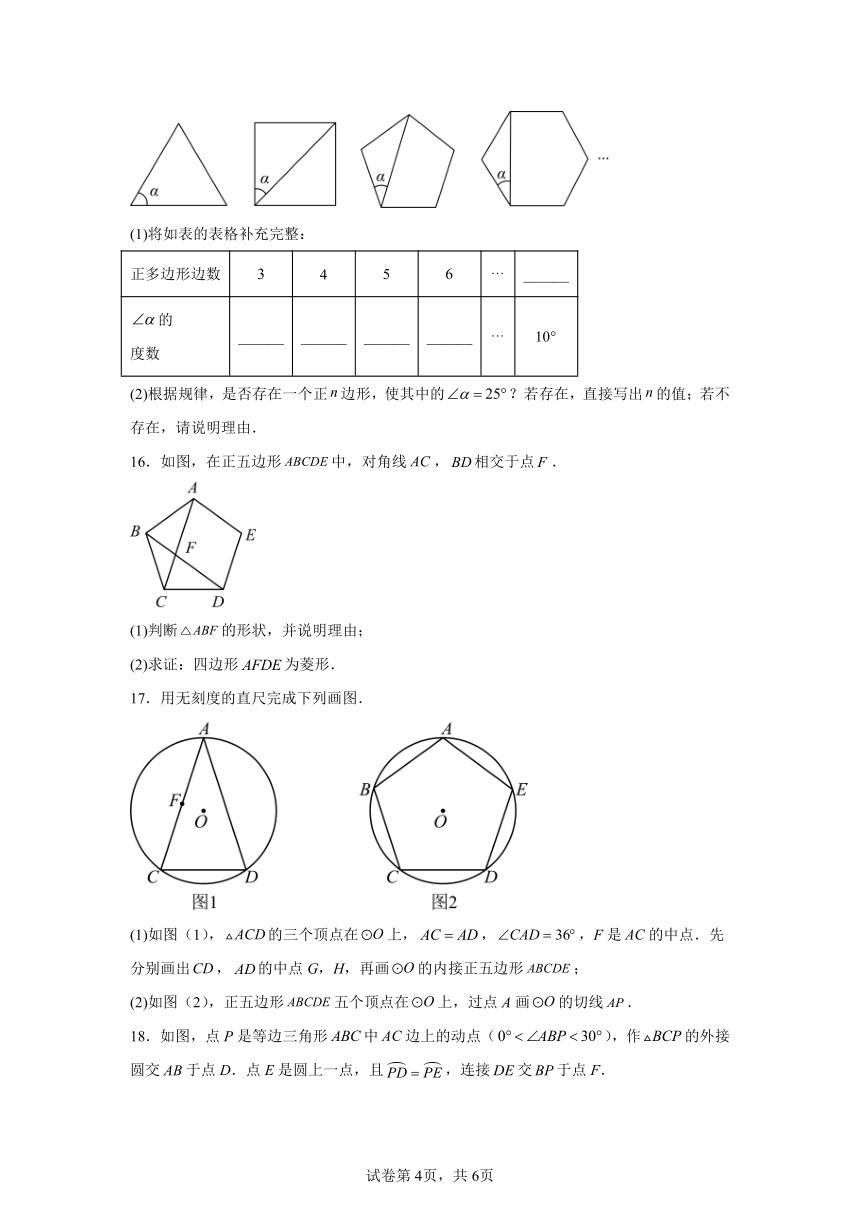
12.如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为,则该半圆的半径为 .
13.如图,正方形内接于,线段在对角线上运动,若的面积为,,则周长的最小值是 .
三、解答题
14.如图,正方形内接于,其边长为4,求的内接正三角形的边长.
15.我们学习了,多边形中,如果各条边都相等,各个内角都相等,这样的多边形叫做正多边形观察每个正多边形中的变化情况,解答下列问题:
(1)将如表的表格补充完整:
正多边形边数 ______
的 度数 ______ ______ ______ ______
(2)根据规律,是否存在一个正边形,使其中的?若存在,直接写出的值;若不存在,请说明理由.
16.如图,在正五边形中,对角线,相交于点.
(1)判断的形状,并说明理由;
(2)求证:四边形为菱形.
17.用无刻度的直尺完成下列画图.
(1)如图(1),的三个顶点在上,,,F是的中点.先分别画出,的中点G,H,再画的内接正五边形;
(2)如图(2),正五边形五个顶点在上,过点A画的切线.
18.如图,点P是等边三角形中边上的动点(),作的外接圆交于点D.点E是圆上一点,且,连接交于点F.
(1)求证:
(2)当点P运动变化时,的度数是否发生变化?若变化,请说明理由;若不变,求的度数.
(3)探究线段、、之间的数量关系,并证明.
19.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,连结EB,交OD于点F.
(1)求证:OD⊥BE.
(2)若DE=,AB=6,求AE的长.
(3)若△CDE的面积是△OBF面积的,求线段BC与AC长度之间的等量关系,并说明理由.
20.有两个内角分别是它们对角的一半的四边形叫做半对角四边形
(1)如图1,在半对角四边形中,,,求与的度数之和;
(2)如图2,锐角 ABC内接于,若边上存在一点,使得,的平分线交于点,连结并延长交于点,.求证:四边形是半对角四边形;
(3)如图3,在(2)的条件下,过点作于点,交于点,当时,求的直径.
试卷第1页,共3页
试卷第1页,共3页
《九年级数学上册人教版第24.3节《正多边形和圆》课时练习题》参考答案
题号 1 2 3 4 5 6 7
答案 C C B A A B A
8.
9.
10.
11./36度
12.
13.4
14.
15.(1)解:正三角形中的度数是正三角形的内角度数,即,
正方形中的度数为,即,
正五边形中的度数为,即,
正六边形中的度数为,即,
正边形中的度数为,即,
当时,即,
解得,
故答案为:,,,,;
(2)由(1)得,正边形中,
当时,即,
解得不是整数,
所以不存在一个正边形,使其中的.
16.(1)∵在正五边形中
∴,
∴
同理可得,
∴
∴
∴
∴
∴是等腰三角形;
(2)由(1)中同理可得,,
∴
∴
∴
∵在正五边形中
∴
∵
∴
∴四边形为菱形.
17.(1)解:如图即为所求.
理由如下:∵,
∴,,
∴,,
∴为的中点,
∵为的中点,
∴过的交点的线段为的中线,
∴为的中点,
∴,,
∴,
∵,
∴为,
∴的度数为,
∴,
∴,
∴五边形为的内角正五边形.
(2)解:如图,延长交于,连接交于,连接并延长交于,过作直线,直线即为所求;
理由:由圆和正五边形的对称性可知,为的中点,
∵正五边形每个内角为,
,
,
,
,
,
,
,
,
,
,
,
,
,
是的半径,
∴直线是的切线.
18.(1)证明:连接PE,
∵△ABC是等边三角形,
∴AB=BC,∠A=∠ACB=60°,
∴∠PEB=∠ACB=60°,
∴∠A=∠PEB,
∵,
∴∠PBD=∠PBE,
∵BP=BP,
∴△ABP≌△EBP(AAS),
∴AB=EB,
∴EB=BC;
(2)解:当点P运动时,∠BFD的度数不会变化,
∵,
∴∠DEP=∠EBP,
∵∠BFD=∠EBP+∠DEB,
∴∠BFD=∠DEP+∠DEB
=∠PEB
=60°,
∴∠BFD的度数为60°;
(3),理由如下:
延长交于点,
,
,
,
是等边三角形,
,
在和中,
,,
,
连接,
四边形是圆的内接四边形,
,
,
,
,
是等边三角形,
,
,即,
在和中,
,
,
,
,
即.
19.(1)连接AD,
∵AB是直径,
∴∠AEB=∠ADB=90°,
∵AB=AC,
∴∠CAD=∠BAD,BD=CD,
∴,
∴OD⊥BE;
(2)∵∠AEB=90°,
∴∠BEC=90°,
∵BD=CD,
∴BC=2DE=2,
∵四边形ABDE内接于⊙O,
∴∠BAC+∠BDE=180°,
∵∠CDE+∠BDE=180°,
∴∠CDE=∠BAC,
∵∠C=∠C,
∴△CDE∽△CAB,
∴,即,
∴CE=2,
∴AE=AC-CE=AB-CE=4;
(3)∵BD=CD,
∴S△CDE=S△BDE,
∵BD=CD,AO=BO,
∴OD∥AC,
∵△OBF∽△ABE,
∴,
∴S△ABE=4S△OBF,
∵,
∴S△ABE=4S△OBF=6S△CDE,
∴S△CAB=S△CDE+S△BDE+S△ABE=8S△CDE,
∵△CDE∽△CAB,
∴,
∴,
∵BD=CD,AB=AC,
∴,即AC=BC.
20.(1)在半对角四边形中,,,
,
,
,
即与的度数和为;
(2)在和中
,
,
,
,
连接,
设,则,
,
,
,
,
,
四边形是半对角四边形;
(3)过点作于,
四边形是半对角四边形,
,
,
,
,
,
,,
,
,
的直径为.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,以点为圆心的两个同心圆把以为半径的大圆的面积三等分,这两个圆的半径分别为,.则的值是( )
A. B. C. D.
2.若正多边形的一个外角为,则这个正多边形的中心角的度数是( )
A. B. C. D.
3.如图所示,某同学作了一个圆内接正十二边形.若的半径为1,则这个圆内接正十二边形的面积为( )
A.1 B.3 C. D.
4.同一个圆的内角正三角形、正方形、正六边形的边心距的比为( )
A. B. C. D.
5.如图,的半径为, ABC是的内接等边三角形,点在上.四边形为平行四边形,则平行四边形的面积是( )
A.4 B.4 C.2 D.2
6.对于下列说法:①正多边形既是轴对称图形,又是中心对称图形;②正多边形一定有内切圆和外接圆;③有一个内切圆和一个外接圆的多边形一定是正多边形;④各边相等的圆内接多边形是正多边形,你认为正确的有( )
A.个 B.个 C.个 D.个
7.如图,点A、B、C、D为一个正多边形的顶点,点O为正多边形的中心,若,则这个正多边形的边数为( )
A.10 B.12 C.15 D.20
二、填空题
8.若正多边形的中心角为,则该正多边形的边数为 .
9.如图,若的半径为1,则的内接正八边形的面积为 .
10.如图,正方形的边长为,剪去个角后成为正八边形,则正八边形的边长为 .
11.如图,正五边形内接于,点在弧上,则的度数为 .
12.如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为,则该半圆的半径为 .
13.如图,正方形内接于,线段在对角线上运动,若的面积为,,则周长的最小值是 .
三、解答题
14.如图,正方形内接于,其边长为4,求的内接正三角形的边长.
15.我们学习了,多边形中,如果各条边都相等,各个内角都相等,这样的多边形叫做正多边形观察每个正多边形中的变化情况,解答下列问题:
(1)将如表的表格补充完整:
正多边形边数 ______
的 度数 ______ ______ ______ ______
(2)根据规律,是否存在一个正边形,使其中的?若存在,直接写出的值;若不存在,请说明理由.
16.如图,在正五边形中,对角线,相交于点.
(1)判断的形状,并说明理由;
(2)求证:四边形为菱形.
17.用无刻度的直尺完成下列画图.
(1)如图(1),的三个顶点在上,,,F是的中点.先分别画出,的中点G,H,再画的内接正五边形;
(2)如图(2),正五边形五个顶点在上,过点A画的切线.
18.如图,点P是等边三角形中边上的动点(),作的外接圆交于点D.点E是圆上一点,且,连接交于点F.
(1)求证:
(2)当点P运动变化时,的度数是否发生变化?若变化,请说明理由;若不变,求的度数.
(3)探究线段、、之间的数量关系,并证明.
19.如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,连结EB,交OD于点F.
(1)求证:OD⊥BE.
(2)若DE=,AB=6,求AE的长.
(3)若△CDE的面积是△OBF面积的,求线段BC与AC长度之间的等量关系,并说明理由.
20.有两个内角分别是它们对角的一半的四边形叫做半对角四边形
(1)如图1,在半对角四边形中,,,求与的度数之和;
(2)如图2,锐角 ABC内接于,若边上存在一点,使得,的平分线交于点,连结并延长交于点,.求证:四边形是半对角四边形;
(3)如图3,在(2)的条件下,过点作于点,交于点,当时,求的直径.
试卷第1页,共3页
试卷第1页,共3页
《九年级数学上册人教版第24.3节《正多边形和圆》课时练习题》参考答案
题号 1 2 3 4 5 6 7
答案 C C B A A B A
8.
9.
10.
11./36度
12.
13.4
14.
15.(1)解:正三角形中的度数是正三角形的内角度数,即,
正方形中的度数为,即,
正五边形中的度数为,即,
正六边形中的度数为,即,
正边形中的度数为,即,
当时,即,
解得,
故答案为:,,,,;
(2)由(1)得,正边形中,
当时,即,
解得不是整数,
所以不存在一个正边形,使其中的.
16.(1)∵在正五边形中
∴,
∴
同理可得,
∴
∴
∴
∴
∴是等腰三角形;
(2)由(1)中同理可得,,
∴
∴
∴
∵在正五边形中
∴
∵
∴
∴四边形为菱形.
17.(1)解:如图即为所求.
理由如下:∵,
∴,,
∴,,
∴为的中点,
∵为的中点,
∴过的交点的线段为的中线,
∴为的中点,
∴,,
∴,
∵,
∴为,
∴的度数为,
∴,
∴,
∴五边形为的内角正五边形.
(2)解:如图,延长交于,连接交于,连接并延长交于,过作直线,直线即为所求;
理由:由圆和正五边形的对称性可知,为的中点,
∵正五边形每个内角为,
,
,
,
,
,
,
,
,
,
,
,
,
,
是的半径,
∴直线是的切线.
18.(1)证明:连接PE,
∵△ABC是等边三角形,
∴AB=BC,∠A=∠ACB=60°,
∴∠PEB=∠ACB=60°,
∴∠A=∠PEB,
∵,
∴∠PBD=∠PBE,
∵BP=BP,
∴△ABP≌△EBP(AAS),
∴AB=EB,
∴EB=BC;
(2)解:当点P运动时,∠BFD的度数不会变化,
∵,
∴∠DEP=∠EBP,
∵∠BFD=∠EBP+∠DEB,
∴∠BFD=∠DEP+∠DEB
=∠PEB
=60°,
∴∠BFD的度数为60°;
(3),理由如下:
延长交于点,
,
,
,
是等边三角形,
,
在和中,
,,
,
连接,
四边形是圆的内接四边形,
,
,
,
,
是等边三角形,
,
,即,
在和中,
,
,
,
,
即.
19.(1)连接AD,
∵AB是直径,
∴∠AEB=∠ADB=90°,
∵AB=AC,
∴∠CAD=∠BAD,BD=CD,
∴,
∴OD⊥BE;
(2)∵∠AEB=90°,
∴∠BEC=90°,
∵BD=CD,
∴BC=2DE=2,
∵四边形ABDE内接于⊙O,
∴∠BAC+∠BDE=180°,
∵∠CDE+∠BDE=180°,
∴∠CDE=∠BAC,
∵∠C=∠C,
∴△CDE∽△CAB,
∴,即,
∴CE=2,
∴AE=AC-CE=AB-CE=4;
(3)∵BD=CD,
∴S△CDE=S△BDE,
∵BD=CD,AO=BO,
∴OD∥AC,
∵△OBF∽△ABE,
∴,
∴S△ABE=4S△OBF,
∵,
∴S△ABE=4S△OBF=6S△CDE,
∴S△CAB=S△CDE+S△BDE+S△ABE=8S△CDE,
∵△CDE∽△CAB,
∴,
∴,
∵BD=CD,AB=AC,
∴,即AC=BC.
20.(1)在半对角四边形中,,,
,
,
,
即与的度数和为;
(2)在和中
,
,
,
,
连接,
设,则,
,
,
,
,
,
四边形是半对角四边形;
(3)过点作于,
四边形是半对角四边形,
,
,
,
,
,
,,
,
,
的直径为.
答案第1页,共2页
答案第1页,共2页
同课章节目录
