(小升初开学分班考)小升初开学择校分班摸底冲刺卷-2025年秋六年级数学人教版(含答案解析)
文档属性
| 名称 | (小升初开学分班考)小升初开学择校分班摸底冲刺卷-2025年秋六年级数学人教版(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 120.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 22:49:50 | ||
图片预览




文档简介
/ 让学习更有效 小升初备考 | 数学学科
2025年秋六年级数学小升初开学择校分班摸底冲刺卷(人教版)
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题
1.已知a、b均是大于1的自然数,且a是b的倍数,则下面的说法,错误的是( )
A.b是a的因数
B.a是a与b的公倍数
C.a与b的和一定是偶数
D.a与b的积一定不是质数
2.有两个相关联的量,它们的关系如图所示,这两个量可能是( )
A.一个人的身高和她的年龄 B.x和y,并且满足
C.圆的周长和它的直径 D.圆柱的底面积和它的高(它的体积一定)
3.小亮同学分别用8个1cm3的正方体测量了4个盒子的容积(如图),第( )个盒子的容积最大。
A. B.
C. D.
4.小红买了a千克西红柿,每千克5元;又买了b千克黄瓜,每千克6元。那么5a﹣6b表示( )
A.买西红柿和黄瓜共付的钱数
B.买黄瓜比西红柿少付的钱数
C.西红柿比黄瓜重的千克数
D.每千克西红柿比每千克黄瓜贵的钱数
5.如图,将圆柱形玻璃杯的水倒入下面编号为( )号圆锥形容器里,正好倒满(单位:厘米)。
A. B. C. D.
6.在带有正、负数的直线上表示0.3、﹣1、、,其中与0最接近的是( )
A.0.3 B.﹣1 C. D.
7.丁丁花15元钱买了5块橡皮。冬冬比丁丁多花3元钱,买了2支彩笔。冬冬花了多少钱?解答这个问题需要用到的信息是 ( )
A.15元、5块、3元、2支 B.15元、3元、2支
C.15元、3元 D.3元
8.一个三角形,三个内角度数的比是1:2:3,这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等边三角形
9.抽签表演节目(其中:讲故事2张、唱歌9张、跳舞3张、魔术1张),如果小红在这些节目中任意抽一张,根据可能性大小判断,最有可能抽到( )
A.讲故事 B.唱歌 C.跳舞 D.魔术
10.图显示了甲、乙两台电脑的价格以及它们已使用的年数,从图中可以知道( )
A.甲比乙旧,且甲比乙价格便宜
B.甲比乙新,且甲比乙价格便宜
C.甲比乙旧,且甲比乙价格贵
D.甲比乙新,且甲比乙价格贵
二.填空题
11.2021年增城区全区实现地区生产总值一千二百六十六亿六千六百万元,横线上的数写作 。2021年增城区常住人口1466300人,横线上的数改写成用“万”作单位的数是 万人(结果保留整数)。
12.:0.25的最简整数比是 ,比值是 。
13.(1)一个自然数既是3的倍数,又是15的因数,这个数是 或是 。
(2)六年级同学做操,无论是每16人一行还是每12人一行,都正好排完,已知六年级不超60人,六年级有 人。
14.在如图中,圆锥、圆柱、正方体的底面积相等,高也相等。正方体的体积是 dm3,圆柱的底面积是 dm2。
15.这是小红做的一道作业题:5.98÷0.23=2.51。你认为她算对了吗?如果不列竖式进行笔算,你有办法判断出小红的计算结果是否正确吗?说说你的想法: 。
16.一个数由1个亿、4个百万、3个十、6个0.1组成,这个数写作 ,读作 ,省略万位后的尾数得到 万。
17.4000dm2= m2 8.3L= mL 2时30分= 时
18.张叔叔的劳务收入是1.5万元,按规定需缴纳20%的个人所得税,张叔叔实际得到了 元。
19.去年“五一”劳动节当天,某公园的游客数量约2万人次。今年“五一”当天的游客数量比去年增加了八成,今年“五一”当天的游客数量是 万人次。
20.爷爷今年80岁,爸爸年龄是爷爷的,而我的年龄恰巧是爸爸的。我今年 岁。
21.张老师带100元去书店买词典。每本词典18.5元,他最多可以买 本。
22.一个直角三角形两条直角边分别是3cm和2cm,以3cm的直角边为轴旋转一周,可得到一个 ,体积是 cm3。(用含π的式子表示最简结果)
三.判断题
23.一个底面直径和高相等的圆柱,侧面沿高展开后得到一个正方形。
24.长方形、正方形、三角形、圆和梯形都是轴对称图形. .
25.在含盐30%的盐水中,加入6克盐和14克水,这时盐水的含盐百分比是30%. .
26.一种商品提价10%后,销量大减,于是商家又降价10%出售.现在的价格比最初的价格降低. .
27.三天后一定会下雪。
28.一根木头锯4段用12分,如果锯6段,那么要用20分。
四.计算题
29.直接写出得数。
8.4 70×40%= 30
5.7﹣3.12= 1 7.4+6=
3.6÷0.4=
30.解比例。
(1) (2)x::10
31.计算下列各题,能用简便方法的要用简便方法计算。
(1)20.5﹣6 (2)12
(3)2 []
五.操作题(共1小题)
32.如图每个小正方形的边长表示1cm。
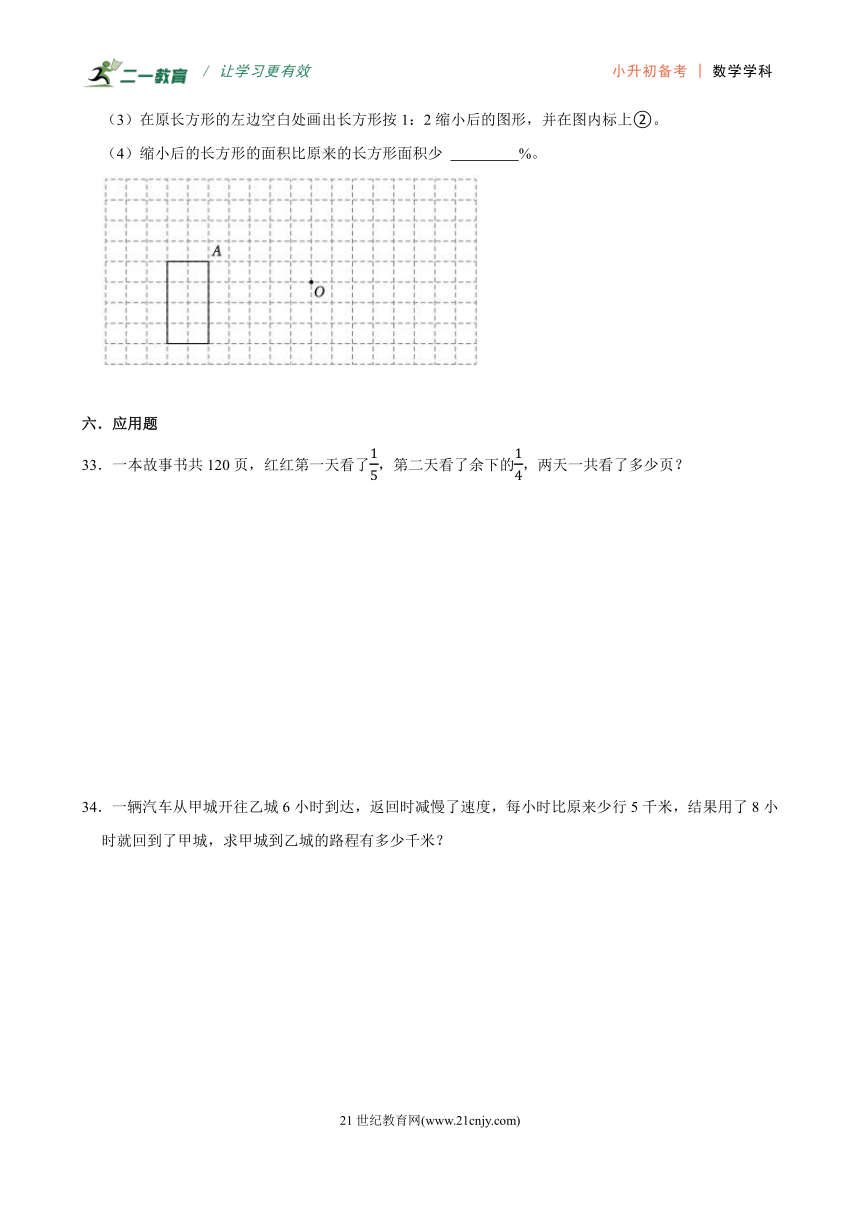
(1)画出长方形绕点A顺时针旋转90°后的图形,并在图内标上①。
(2)以点O为圆心,画一个半径是3cm的圆。
(3)在原长方形的左边空白处画出长方形按1:2缩小后的图形,并在图内标上②。
(4)缩小后的长方形的面积比原来的长方形面积少 %。
六.应用题
33.一本故事书共120页,红红第一天看了,第二天看了余下的,两天一共看了多少页?
34.一辆汽车从甲城开往乙城6小时到达,返回时减慢了速度,每小时比原来少行5千米,结果用了8小时就回到了甲城,求甲城到乙城的路程有多少千米?
35.王大伯屋后有一棵桃树,他调皮的孙子每天从树上摘下一些桃子和邻居的小伙伴分吃。第一天摘下桃子总个数的,以后的8天分别摘下当天现有桃子的、、、,摘了9天,树上还留下10个桃子。树上原来有多少个桃子?
36.布艺兴趣小组用8米布制作一批帽子,每顶帽子用布米,将这些帽子的送给养老院。送给养老院多少顶帽子?
37.学校有象棋、跳棋共26副,2名学生下1副象棋,6名学生下1副跳棋,恰好可以同时供120名学生活动.象棋与跳棋各有多少副?
38.学校组织同学参观爱国主义图片展,每60名同学聘请2名讲解员作介绍。全校960名同学参观,需要聘请几名讲解员?(用比例知识解答)
参考答案及试题解析
一.选择题
1.【考点】因数和倍数的意义;合数与质数的初步认识;奇数与偶数的初步认识.
【答案】C
【思路分析】若整数a能够被b整除,a叫做b的倍数,b就叫做a的因数,因数与倍数是相互依存的,据此解答。
【解答】解:A.已知a、b均是大于1的自然数,且a是b的倍数,说明b是a的因数,说法正确;
B.a是a的最小倍数,也是b的倍数,因此a是它们的公倍数,说法正确;
D.a与b的积至少有1和a和b这3个因数,因此一定不是质数,说法正确。
只有选项C说法错误,a与b的和可能是偶数,也可能是奇数。
故选:C。
【名师点评】本题主要考查因数与倍数的意义,注意因数与倍数是相互依存的。
2.【考点】辨识成正比例的量与成反比例的量;圆柱的侧面积、表面积和体积.
【答案】C
【思路分析】由图像是一条经过原点的直线可知,这两个相关联的量成正比例关系,判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。据此解答。
【解答】解:A.一个人的身高和她的年龄不成比例,通常在生长期,人的身高是随着年龄的增长而增长,但是生长期过了后,骨膜会闭合,停止长高;
B.因为,所以xy=6(一定),乘积一定,所以x和y成反比例;
C.圆的周长÷它的直径=π(一定),商一定,所以圆的周长和它的直径成正比例;
D.圆柱的底面积×它的高=圆柱的体积(一定),乘积一定,所以圆柱的底面积和它的高成反比例。
故选:C。
【名师点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
3.【考点】体积、容积及其单位;长方体和正方体的体积.
【答案】A
【思路分析】根据长方体的体积=长×宽×高,求出体积,再比较大小即可。
【解答】解:的容积=4×3×3=36(立方厘米);的容积=5×4×1=20(立方厘米);的容积=4×4×2=32(立方厘米);的容积=3×2×3=18(立方厘米)。
所以的容积最大。
故选:A。
【名师点评】熟练掌握长方体的体积公式,是解答此题的关键。
4.【考点】用字母表示数.
【答案】B
【思路分析】根据题意,找出5a和6b的意义,完成选择。
【解答】解:5a表示5千克西红柿的钱数;6b表示6千克黄瓜的钱数。
所以5a﹣6b表示买6千克黄瓜比买5千克西红柿少付的钱数。
故选:B。
【名师点评】本题主要考查字母表示数。
5.【考点】圆锥的体积;圆柱的侧面积、表面积和体积.
【答案】C
【思路分析】等底等高的圆柱的体积是圆锥体积的3倍,根据求一个数的几倍是多少,用乘法解答。
【解答】解:6×3=18(厘米)
选择高为18厘米的圆锥形容器。
故选:C。
【名师点评】此题考查的目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及应用。
6.【考点】数轴的认识;正、负数大小的比较.
【答案】D
【思路分析】从原点出发,朝正方向的射线(正半轴)上的点对应正数,相反方向的射线(负半轴)上的点对应负数,原点对应零;在数轴上表示的两个数,右边的数总比左边的数大;正数都大于0,负数都小于0,正数大于一切负数。据此解答。
【解答】解:
通过数轴发现与0最接近。
故选:D。
【名师点评】本题是考查数轴的认识.数轴是规定了原点(0点)、方向和单位长度的一条直线。
7.【考点】“提问题”、“填条件”应用题.
【答案】C
【思路分析】冬冬花的钱数=丁丁花的钱数+3元,据此解答即可。
【解答】解:15+3=18(元)
答:冬冬花了18元。
故选:C。
【名师点评】找出题目中的数量关系,是解答此题的关键。
8.【考点】三角形的分类;三角形的内角和;按比例分配应用题.
【答案】B
【思路分析】因为三角形的内角度数和是180°,三角形的最大的角的度数占内角度数和的,根据一个数乘分数的意义,求出最大角,进而判断即可.
【解答】解:1+2+3=6,
最大的角:180°90°,所以这个三角形是直角三角形;
故选:B。
【名师点评】解答此题应明确三角形的内角度数的和是180°,求出最大的角的度数,然后根据三角形的分类判定类型.
9.【考点】可能性的大小.
【答案】B
【思路分析】不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小,数量相同,可能性也相同。
【解答】解:因为写有唱歌的签最多,所以小红在这些节目中任意抽一张,根据可能性大小判断,最有可能抽到唱歌。
故选:B。
【名师点评】本题考查可能性大小的判断,解题关键是理解并掌握影响可能性大小的因素,理解哪种节目的卡片多,抽到哪种节目的可能性就大,反之则越小。
10.【考点】从统计图表中获取信息.
【答案】D
【思路分析】根据图可以看出,横轴代表年份,纵轴代表价格,横轴的位置离交点越远则年份越多,纵轴的位置离交点越远则价格越高,据此可以解答。
【解答】解:横轴的位置离交点越远则年份越多,纵轴的位置离交点越远则价格越高,所以甲比乙新,且甲比乙价格贵。
故选:D。
【名师点评】此题考查了学生通过观察统计图从统计图中获取信息的能力。
二.填空题
11.【考点】亿以上数的改写与近似.
【答案】126666000000,147。
【思路分析】根据整数的写法,从高位到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0;改写成用“万”作单位的数,就是把千位上的数进行四舍五入,再在数的后面写上“万”字;结果保留整数,就是将十分位上的数四舍五入到个位。
【解答】解:2021年增城区全区实现地区生产总值一千二百六十六亿六千六百万元,横线上的数写作126666000000。2021年增城区常住人口1466300人,横线上的数改写成用“万”作单位的数是147万人(结果保留整数)。
故答案为:126666000000,147。
【名师点评】本题主要考查整数的写法和求近似数,求近似数时要注意带计数单位。
12.【考点】求比值和化简比.
【答案】见试题解答内容
【思路分析】根据比的基本性质,:0.25的前、后项都乘8即可将此比化成最简整数比;根据比值的意义,比的前项除以后项的商就是比值。
【解答】解::0.25=3:2
=3:2
=3÷2
=1.5
答::0.25的最简整数比是3:2,比值是1.5。
故答案为:3:2,1.5。
【名师点评】此题是考查比的化简与求比值,属于基础知识,要掌握。
13.【考点】找一个数的倍数的方法;公因数和公倍数应用题;找一个数的因数的方法.
【答案】3,15;48。
【思路分析】(1)15以内,3的倍数有3、6、9、12、15。15的因数有1、3、5、15。找出既是3的倍数,又是15的因数即可解答。
(2)根据求最小公倍数的方法,求出16和12的最小公倍数,找出小于60人的倍数即可。
【解答】解:(1)3的倍数有3、6、9、12、15……。15的因数有1、3、5、1^既是3的倍数,又是15的因数,这个数是3或是15。
(2)16=2×2×2×2,12=2×2×3,16和12的最小公倍数是2×2×2×2×3=48;
48×2=96
96>60
48<60
六年级有48人。
故答案为:3,15;48。
【名师点评】本题考查公因数和公倍数的计算及应用。
14.【考点】圆柱的侧面积、表面积和体积;长方体和正方体的体积.
【答案】1000,100。
【思路分析】从图上可得:正方体的棱长是10dm,因为圆柱的底面积和正方体的底面积相同,所以根据正方形面积公式S=边长×边长,正方体的体积公式:V=棱长×棱长×棱长,将数据代入,即可得出答案。
【解答】解:10×10×10
=100×10
=1000(dm3)
10×10=100(dm2)
答:正方体的体积是1000dm3,圆柱的底面积是100dm2。
故答案为:1000,100。
【名师点评】本题考查学生对正方形面积和正方体体积的运用,要求学生熟练掌握公式。
15.【考点】小数除法.
【答案】用2.51×0.23验算,2.51和0.23都是两位数小数,则它们的积是4位小数,而5.98只有两位小数,所以是错的。(答案不唯一)
【思路分析】可以用商×除数=被除数的方法进行验算。
【解答】解:用2.51×0.23验算,2.51和0.23都是两位数小数,则它们的积是4位小数,而5.98只有两位小数,所以是错的。(答案不唯一)
故答案为:用2.51×0.23验算,2.51和0.23都是两位数小数,则它们的积是4位小数,而5.98只有两位小数,所以是错的。(答案不唯一)
【名师点评】本题主要考查了通过不计算判断小数除法算式是否正确,可以通过用乘法验算的方法进行判定。
16.【考点】小数的读写、意义及分类;小数的近似数及其求法.
【答案】104000030.6,一亿零四百万零三十点六,10400万。
【思路分析】小数的写法:整数部分按照整数的写法来写(整数部分是零的写作“0”),小数点点在个位的右下角,小数部分顺次写出每一个数位上的数字;
小数的读法:整数部分按整数的读法来读,小数点读作点,小数部分要依次读出每个数字;
省略“万”后面的尾数求它的近似数,要把万位的下一位千位上的数进行四舍五入,再在数的后面带上“万”字;
由此求解。
【解答】解:一个数由1个亿、4个百万、3个十、6个0.1组成,这个数写作104000030.6,读作一亿零四百万零三十点六,省略万位后的尾数得到10400万。
故答案为:104000030.6,一亿零四百万零三十点六,10400万。
【名师点评】本题主要考查小数读、写和求近似数,注意找清楚每一个数位上数字是多少。
17.【考点】小面积单位间的进率及单位换算;体积、容积进率及单位换算;时、分、秒及其关系、单位换算与计算.
【答案】40,8300,2.5。
【思路分析】低级单位平方分米化高级单位平方米除以进率100;
高级单位升化低级单位毫升乘进率1000;
把30分除以进率60化成0.5时,再加2时。
【解答】解:
4000dm2=40m2 8.3L=8300mL 2时30分=2.5时
故答案为:40,8300,2.5。
【名师点评】单位换算首先要弄清是由高级单位化低级单位还是由低级单位化高级单位,其次记住单位间的进率;由高级单位化低级单位乘进率,由低级单位化高级单位除以进率。
18.【考点】存款利息与纳税相关问题.
【答案】12000。
【思路分析】把1.5万元看作单位“1”,1.5万元=15000元,按规定应缴纳20%的个人所得税后剩余的钱就是实际得到的奖金,列式为15000×(1﹣20%),解决问题。
【解答】解:15000×(1﹣20%)
=15000×80%
=12000(元)
答:张叔叔实际得到奖金12000元。
故答案为:12000。
【名师点评】或者用总钱数扣除20%的个人所得税,列式为15000﹣15000×20%。
19.【考点】百分数的实际应用.
【答案】3.6
【思路分析】根据题意:把去年“五一”劳动节当天,公园的游客数量看作单位“1”,根据已知条件可知:今年“五一”当天的游客数量是去年的1+80%=180%,然后根据百分数乘法的意义,求一个数的百分之几用乘法计算,解答此题。
【解答】解:2×(1+80%)
=2×1.8
=3.6(万人次)
答:今年“五一”当天的游客数量是3.6万人次。
故答案为:3.6。
【名师点评】完成本题的关键是熟记关系式:比单位“1”多的公式为:单位“1”的量×(1+百分之几)。
20.【考点】分数乘法应用题.
【答案】12。
【思路分析】把爷爷的年龄看作单位“1”,用爷爷的年龄,可以计算出爸爸的年龄,再用爸爸的年龄乘,可以计算出我的年龄。
【解答】解:
=12(岁)
答:我今年12岁。
故答案为:12。
【名师点评】本题考查分数乘法应用题,解题关键是先找出题目中的单位“1”是哪个量,再根据一个数乘分数的意义,列式计算。
21.【考点】整数、小数复合应用题.
【答案】5。
【思路分析】根据总价÷单价=数量,代入数值即可求出可以买多少本,结尾用去尾法保留整数。
【解答】解:100÷18.5≈5(本)
答:他最多可以买5本。
故答案为:5。
【名师点评】本题主要考查了小数除法的实际应用,注意结尾用去尾法保留整数。
22.【考点】圆锥的体积.
【答案】圆锥体;12.56。
【思路分析】根据题意可知,以直角三角形以3cm的直角边所在直线为轴旋转一周,可以得到一个底面半径是2厘米,高是3厘米的圆锥,根据圆锥的体积=底面积×高÷3,把数据代入公式解答。
【解答】解:3.14×2×2×3÷3
=12.56×3÷3
=12.56(立方厘米)
答:可得到一个圆锥体,体积是12.56cm3。
故答案为:圆锥体;12.56。
【名师点评】此题考查的目的是理解掌握圆锥的特征,以及圆锥体积公式的灵活运用,关键是熟记公式。
三.判断题
23.【考点】圆柱的展开图.
【答案】×
【思路分析】因为将圆柱沿高展开后得到一个长方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高,由此再根据“一个圆柱的侧面展开是一个正方形,”知道圆柱的底面周长与圆柱的高相等。
【解答】解:一个底面周长和高相等的圆柱,侧面沿高展开后得到一个正方形。原题说法错误。
故答案为:×。
【名师点评】此题主要考查了圆柱与圆柱的侧面展开图之间的关系。
24.【考点】轴对称图形的辨识.
【答案】见试题解答内容
【思路分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;进行判断即可.
【解答】解:根据轴对称图形的意义可知:正方形、长方形、圆都是轴对称图形,
而三角形和梯形不一定是轴对称图形,只有等腰三角形和等腰梯形是轴对称图形;
故答案为:×.
【名师点评】此题考查了轴对称图形的意义,判断轴对称图形的关键是寻找对称轴,看图形对折后两部分是否完全重合.
25.【考点】百分数的实际应用.
【答案】见试题解答内容
【思路分析】含盐百分比是指含盐的重量占盐水总重量的百分之几,求出后来加入的盐水的含盐百分比然后与30%比较即可.
【解答】解:6÷(6+14)×100%,
=6÷20×100%,
=30%;
加入的盐水的含盐百分比30%,与原来相同,所以后来的含盐百分比也是30%.
故答案为:√.
【名师点评】本题关键是理解含盐百分比,找出其计算的方法,只要加入的盐水的含盐百分比也是30%,那么后来的盐水的含盐百分比就是30%.
26.【考点】百分数的实际应用.
【答案】见试题解答内容
【思路分析】第一个单位“1”是原价,提价后的价格就是原价的1+10%;第二个10%的单位“1”是提价后的价格,现价是提价后价格的1﹣10%,求出现价再与原价比较即可.
【解答】解:设原价是1,则提价后的价格是:
1×(1+10%)=110%;
现价是:110%×(1﹣10%)
=110%×90%,
=99%;
99%<1,即现价低于原价.
故答案为:√.
【名师点评】解答此题的关键是分清两个单位“1”的区别,找清各自以谁为标准,再把数据设出,根据数量关系求解.
27.【考点】事件的确定性与不确定性.
【答案】×
【思路分析】事件可分为确定事件和不确定事件,确定事件可分为必然事件和不可能事件,不确定事件又称为随机事件。
【解答】解:三天后会不会下雪是未确定事件,所以不能用一定描述,应说三天后可能会下雪。原题说法错误。
故答案为:×。
【名师点评】此题应根据可能性的大小进行分析、解答。
28.【考点】植树问题.
【答案】√
【思路分析】一根木头锯4段,需要锯(4﹣1)次,由此计算出平均每次需要时间,然后计算锯6段的时间,由此解答本题。
【解答】解:12÷(4﹣1)
=12÷3
=4(分)
4×(6﹣1)
=4×5
=20(分)
答:如果锯6段,那么要用20分。
本题说法正确。
故答案为:√。
【名师点评】解决本题的关键是找出题中数量关系。
四.计算题
29.【考点】分数乘除混合运算;分数的四则混合运算;分数除法.
【答案】2.1;28;36;2.58;;13.4;9;;。
【思路分析】计算小数加减法,要相同数位对齐,从低位算起;
小数除法的计算,根据商不变的性质,先移动除数的小数点使它变成整数,再根据除数是整数的除法算出商;
分数乘法的计算法则,分子相乘的积做分子,分母相乘的积做分母;
分数除法的计算法则,除以一个不为0的数等于乘这个数的倒数;
异分母分数相加减,要先通分,化成同分母分数后再计算。
【解答】解:
8.42.1 70×40%=28 3036
5.7﹣3.12=2.58 1 7.4+6=13.4
3.6÷0.4=9
【名师点评】本题解题关键是熟练掌握分数、小数四则运算的计算方法。
30.【考点】解比例.
【答案】(1)x=21;
(2)x。
【思路分析】(1)根据比例的基本性质的性质,把原式化为4x=3×28,然后方程的两边同时除以4求解;
(2)根据比例的基本性质的性质,把原式化为10x,然后方程的两边同时除以10求解。
【解答】解:(1)
4x=3×28
4x÷4=3×28÷4
x=21
(2)x::10
10x
10x÷1010
x
【名师点评】本题考查解方程和解比例,解题的关键是掌握等式的性质与比例的基本性质:方程两边同时加上或减去相同的数,等式仍然成立;方程两边同时乘(或除以)相同的数(0除外),等式仍然成立;两个外项的积等于两个内项的积。
31.【考点】运算定律与简便运算.
【答案】(1)4.5;
(2);
(3)0;
(4)。
【思路分析】(1)先算除法,再算减法;
(2)根据乘法分配律进行计算;
(3)先算除法,再根据减法的性质进行计算;
(4)先算小括号里面的减法,再算中括号里面的除法,最后算括号外面的乘法。
【解答】解:(1)20.5﹣6
=20.5﹣16
=4.5
(2)12
=()
(3)2
=2
=2﹣()
=2﹣2
=0
(4)[]
[]
【名师点评】考查了运算定律与简便运算,四则混合运算。注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
五.操作题(共1小题)
32.【考点】作旋转一定角度后的图形;图形的放大与缩小.
【答案】(1)~(3);
(4)75。
【思路分析】(1)根据旋转的特征,长方形绕点A顺时针旋转90°,点A的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形①。
(2)画圆时,“圆心定位置,半径定大小”,以确定的点O为圆心,以3厘米为半径画圆即可。
(3)根据图形放大与缩小的意义,把长方形的长、宽均缩小到原来的,所得到的图形就是原长方形按1:2缩小后的图形②。
(4)根据长方形的面积计算公式“S=ab”分别计算出原来长方形的面积、缩小后长方形的面积,再用原长方形面积与缩小后长方形面积的差除以原长方形的面积。
【解答】解:(1)~(3)画图如下:
(4)(4×2﹣2×1)÷(4×2)
=(8﹣2)÷8
=6÷8
=0.75
=75%
答:缩小后的长方形的面积比原来的长方形面积少75%。
故答案为:75。
【名师点评】此题考查了作旋转一定度数后的图形、图形的放大与缩小、画圆、百分数的应用。
六.应用题
33.【考点】分数四则复合应用题.
【答案】48页。
【思路分析】根据乘数的意义,第一天看的页数=全书的页数;第二天看的页数=余下的页数;余下的页数=全书页数﹣第一天看的页数;第一天的页数+第二天的页数=两天一共看的页数。
【解答】解:120(120﹣120)
=24+(120﹣24)
=24+96
=24+24
=48(页)
答:两天一共看了48页。
【名师点评】分析题目数量之间的关系,根据数量之间的关系列出数量关系式,根据数量关系式解决问题。
34.【考点】简单的行程问题.
【答案】120千米。
【思路分析】根据题意,这道题的等量关系是:去时的速度×时间=返回时的速度×时间,根据这个等量关系,列方程解答。
【解答】解:设原来每小时行x千米。
6x=(x﹣5)×8
6x=8x﹣40
8x﹣6x=40
2x=40
x=20
20×6=120(千米)
答:甲城到乙城的路程有120千米。
【名师点评】本题考查行程问题的解题方法,用方程解答比较简便,解题关键是找出题目中的等量关系:去时的速度×时间=返回时的速度×时间,列方程解答。
35.【考点】逆推问题.
【答案】100个。
【思路分析】根据题意,把当天桃子总数看作单位“1”,则第9天摘之前树上的桃子数是10÷(1),同理,第8天摘之前树上的桃子是第9天桃子总数(第8天剩下的桃子数)的(1),依此类推,用除法求出桃子总数即可。
【解答】解:10÷(1)÷(1)÷……÷(1)
=10
=10×2
=10×10
=100(个)
答:树上原来有100个桃子。
【名师点评】本题主要考查逆推问题,关键求摘之前树上桃子的数量。
36.【考点】分数四则复合应用题.
【答案】15顶。
【思路分析】先依据顶数=布的长度÷每顶帽子用布长度,求出可制作帽子顶数,并把此看作单位“1”,运用分数乘法意义即可解答。
【解答】解:8
=20
=15(顶)
答:送给养老院15顶帽子。
【名师点评】分数乘法意义是解答本题的依据,关键是求出制作帽子顶数。
37.【考点】鸡兔同笼.
【答案】见试题解答内容
【思路分析】假设全部为跳棋,一共有:26×6=156人,比实际多了156﹣120=36人,这是因为我们把下象棋的人当作了下跳棋的人,每副多算了:6﹣2=4人;所以有象棋:36÷4=9(副),那么跳棋就为:26﹣9=17(副);据此解答.
【解答】解:假设全部为跳棋,
象棋:(26×6﹣120)÷(6﹣2)
=36÷4
=9(副)
跳棋:26﹣9=17(副)
答:象棋有9副,跳棋有17副.
【名师点评】解决鸡兔同笼问题往往用假设法解答,有些应用题中有两个或两个以上的未知量,思考问题时,可以假设要求的两个或两个以上的未知量相等,或假设它们为同一种量,然后按照题中的已知条件进行推算,如果数量上出现矛盾,可适当调整,以求出正确的结果.
38.【考点】正、反比例应用题.
【答案】32名。
【思路分析】根据每60名同学聘请2名讲解员作介绍,那么每(60÷2)名同学聘请1名讲解员作介绍(一定),学生人数与讲解员成正比例;设全校960名同学参观,需要聘请x名讲解员,即可列出比例解答。
【解答】解:设全校960名同学参观,需要聘请x名讲解员。
960:x=60:2
60x=960×2
60x=1920
x=32
答:需要聘请32名讲解员。
【名师点评】确定正、反比例是解答关键。
21世纪教育网(www.21cnjy.com)
2025年秋六年级数学小升初开学择校分班摸底冲刺卷(人教版)
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题
1.已知a、b均是大于1的自然数,且a是b的倍数,则下面的说法,错误的是( )
A.b是a的因数
B.a是a与b的公倍数
C.a与b的和一定是偶数
D.a与b的积一定不是质数
2.有两个相关联的量,它们的关系如图所示,这两个量可能是( )
A.一个人的身高和她的年龄 B.x和y,并且满足
C.圆的周长和它的直径 D.圆柱的底面积和它的高(它的体积一定)
3.小亮同学分别用8个1cm3的正方体测量了4个盒子的容积(如图),第( )个盒子的容积最大。
A. B.
C. D.
4.小红买了a千克西红柿,每千克5元;又买了b千克黄瓜,每千克6元。那么5a﹣6b表示( )
A.买西红柿和黄瓜共付的钱数
B.买黄瓜比西红柿少付的钱数
C.西红柿比黄瓜重的千克数
D.每千克西红柿比每千克黄瓜贵的钱数
5.如图,将圆柱形玻璃杯的水倒入下面编号为( )号圆锥形容器里,正好倒满(单位:厘米)。
A. B. C. D.
6.在带有正、负数的直线上表示0.3、﹣1、、,其中与0最接近的是( )
A.0.3 B.﹣1 C. D.
7.丁丁花15元钱买了5块橡皮。冬冬比丁丁多花3元钱,买了2支彩笔。冬冬花了多少钱?解答这个问题需要用到的信息是 ( )
A.15元、5块、3元、2支 B.15元、3元、2支
C.15元、3元 D.3元
8.一个三角形,三个内角度数的比是1:2:3,这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等边三角形
9.抽签表演节目(其中:讲故事2张、唱歌9张、跳舞3张、魔术1张),如果小红在这些节目中任意抽一张,根据可能性大小判断,最有可能抽到( )
A.讲故事 B.唱歌 C.跳舞 D.魔术
10.图显示了甲、乙两台电脑的价格以及它们已使用的年数,从图中可以知道( )
A.甲比乙旧,且甲比乙价格便宜
B.甲比乙新,且甲比乙价格便宜
C.甲比乙旧,且甲比乙价格贵
D.甲比乙新,且甲比乙价格贵
二.填空题
11.2021年增城区全区实现地区生产总值一千二百六十六亿六千六百万元,横线上的数写作 。2021年增城区常住人口1466300人,横线上的数改写成用“万”作单位的数是 万人(结果保留整数)。
12.:0.25的最简整数比是 ,比值是 。
13.(1)一个自然数既是3的倍数,又是15的因数,这个数是 或是 。
(2)六年级同学做操,无论是每16人一行还是每12人一行,都正好排完,已知六年级不超60人,六年级有 人。
14.在如图中,圆锥、圆柱、正方体的底面积相等,高也相等。正方体的体积是 dm3,圆柱的底面积是 dm2。
15.这是小红做的一道作业题:5.98÷0.23=2.51。你认为她算对了吗?如果不列竖式进行笔算,你有办法判断出小红的计算结果是否正确吗?说说你的想法: 。
16.一个数由1个亿、4个百万、3个十、6个0.1组成,这个数写作 ,读作 ,省略万位后的尾数得到 万。
17.4000dm2= m2 8.3L= mL 2时30分= 时
18.张叔叔的劳务收入是1.5万元,按规定需缴纳20%的个人所得税,张叔叔实际得到了 元。
19.去年“五一”劳动节当天,某公园的游客数量约2万人次。今年“五一”当天的游客数量比去年增加了八成,今年“五一”当天的游客数量是 万人次。
20.爷爷今年80岁,爸爸年龄是爷爷的,而我的年龄恰巧是爸爸的。我今年 岁。
21.张老师带100元去书店买词典。每本词典18.5元,他最多可以买 本。
22.一个直角三角形两条直角边分别是3cm和2cm,以3cm的直角边为轴旋转一周,可得到一个 ,体积是 cm3。(用含π的式子表示最简结果)
三.判断题
23.一个底面直径和高相等的圆柱,侧面沿高展开后得到一个正方形。
24.长方形、正方形、三角形、圆和梯形都是轴对称图形. .
25.在含盐30%的盐水中,加入6克盐和14克水,这时盐水的含盐百分比是30%. .
26.一种商品提价10%后,销量大减,于是商家又降价10%出售.现在的价格比最初的价格降低. .
27.三天后一定会下雪。
28.一根木头锯4段用12分,如果锯6段,那么要用20分。
四.计算题
29.直接写出得数。
8.4 70×40%= 30
5.7﹣3.12= 1 7.4+6=
3.6÷0.4=
30.解比例。
(1) (2)x::10
31.计算下列各题,能用简便方法的要用简便方法计算。
(1)20.5﹣6 (2)12
(3)2 []
五.操作题(共1小题)
32.如图每个小正方形的边长表示1cm。
(1)画出长方形绕点A顺时针旋转90°后的图形,并在图内标上①。
(2)以点O为圆心,画一个半径是3cm的圆。
(3)在原长方形的左边空白处画出长方形按1:2缩小后的图形,并在图内标上②。
(4)缩小后的长方形的面积比原来的长方形面积少 %。
六.应用题
33.一本故事书共120页,红红第一天看了,第二天看了余下的,两天一共看了多少页?
34.一辆汽车从甲城开往乙城6小时到达,返回时减慢了速度,每小时比原来少行5千米,结果用了8小时就回到了甲城,求甲城到乙城的路程有多少千米?
35.王大伯屋后有一棵桃树,他调皮的孙子每天从树上摘下一些桃子和邻居的小伙伴分吃。第一天摘下桃子总个数的,以后的8天分别摘下当天现有桃子的、、、,摘了9天,树上还留下10个桃子。树上原来有多少个桃子?
36.布艺兴趣小组用8米布制作一批帽子,每顶帽子用布米,将这些帽子的送给养老院。送给养老院多少顶帽子?
37.学校有象棋、跳棋共26副,2名学生下1副象棋,6名学生下1副跳棋,恰好可以同时供120名学生活动.象棋与跳棋各有多少副?
38.学校组织同学参观爱国主义图片展,每60名同学聘请2名讲解员作介绍。全校960名同学参观,需要聘请几名讲解员?(用比例知识解答)
参考答案及试题解析
一.选择题
1.【考点】因数和倍数的意义;合数与质数的初步认识;奇数与偶数的初步认识.
【答案】C
【思路分析】若整数a能够被b整除,a叫做b的倍数,b就叫做a的因数,因数与倍数是相互依存的,据此解答。
【解答】解:A.已知a、b均是大于1的自然数,且a是b的倍数,说明b是a的因数,说法正确;
B.a是a的最小倍数,也是b的倍数,因此a是它们的公倍数,说法正确;
D.a与b的积至少有1和a和b这3个因数,因此一定不是质数,说法正确。
只有选项C说法错误,a与b的和可能是偶数,也可能是奇数。
故选:C。
【名师点评】本题主要考查因数与倍数的意义,注意因数与倍数是相互依存的。
2.【考点】辨识成正比例的量与成反比例的量;圆柱的侧面积、表面积和体积.
【答案】C
【思路分析】由图像是一条经过原点的直线可知,这两个相关联的量成正比例关系,判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。据此解答。
【解答】解:A.一个人的身高和她的年龄不成比例,通常在生长期,人的身高是随着年龄的增长而增长,但是生长期过了后,骨膜会闭合,停止长高;
B.因为,所以xy=6(一定),乘积一定,所以x和y成反比例;
C.圆的周长÷它的直径=π(一定),商一定,所以圆的周长和它的直径成正比例;
D.圆柱的底面积×它的高=圆柱的体积(一定),乘积一定,所以圆柱的底面积和它的高成反比例。
故选:C。
【名师点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
3.【考点】体积、容积及其单位;长方体和正方体的体积.
【答案】A
【思路分析】根据长方体的体积=长×宽×高,求出体积,再比较大小即可。
【解答】解:的容积=4×3×3=36(立方厘米);的容积=5×4×1=20(立方厘米);的容积=4×4×2=32(立方厘米);的容积=3×2×3=18(立方厘米)。
所以的容积最大。
故选:A。
【名师点评】熟练掌握长方体的体积公式,是解答此题的关键。
4.【考点】用字母表示数.
【答案】B
【思路分析】根据题意,找出5a和6b的意义,完成选择。
【解答】解:5a表示5千克西红柿的钱数;6b表示6千克黄瓜的钱数。
所以5a﹣6b表示买6千克黄瓜比买5千克西红柿少付的钱数。
故选:B。
【名师点评】本题主要考查字母表示数。
5.【考点】圆锥的体积;圆柱的侧面积、表面积和体积.
【答案】C
【思路分析】等底等高的圆柱的体积是圆锥体积的3倍,根据求一个数的几倍是多少,用乘法解答。
【解答】解:6×3=18(厘米)
选择高为18厘米的圆锥形容器。
故选:C。
【名师点评】此题考查的目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及应用。
6.【考点】数轴的认识;正、负数大小的比较.
【答案】D
【思路分析】从原点出发,朝正方向的射线(正半轴)上的点对应正数,相反方向的射线(负半轴)上的点对应负数,原点对应零;在数轴上表示的两个数,右边的数总比左边的数大;正数都大于0,负数都小于0,正数大于一切负数。据此解答。
【解答】解:
通过数轴发现与0最接近。
故选:D。
【名师点评】本题是考查数轴的认识.数轴是规定了原点(0点)、方向和单位长度的一条直线。
7.【考点】“提问题”、“填条件”应用题.
【答案】C
【思路分析】冬冬花的钱数=丁丁花的钱数+3元,据此解答即可。
【解答】解:15+3=18(元)
答:冬冬花了18元。
故选:C。
【名师点评】找出题目中的数量关系,是解答此题的关键。
8.【考点】三角形的分类;三角形的内角和;按比例分配应用题.
【答案】B
【思路分析】因为三角形的内角度数和是180°,三角形的最大的角的度数占内角度数和的,根据一个数乘分数的意义,求出最大角,进而判断即可.
【解答】解:1+2+3=6,
最大的角:180°90°,所以这个三角形是直角三角形;
故选:B。
【名师点评】解答此题应明确三角形的内角度数的和是180°,求出最大的角的度数,然后根据三角形的分类判定类型.
9.【考点】可能性的大小.
【答案】B
【思路分析】不确定事件发生的可能性的大小与事物的数量有关,数量越多,可能性越大,反之则越小,数量相同,可能性也相同。
【解答】解:因为写有唱歌的签最多,所以小红在这些节目中任意抽一张,根据可能性大小判断,最有可能抽到唱歌。
故选:B。
【名师点评】本题考查可能性大小的判断,解题关键是理解并掌握影响可能性大小的因素,理解哪种节目的卡片多,抽到哪种节目的可能性就大,反之则越小。
10.【考点】从统计图表中获取信息.
【答案】D
【思路分析】根据图可以看出,横轴代表年份,纵轴代表价格,横轴的位置离交点越远则年份越多,纵轴的位置离交点越远则价格越高,据此可以解答。
【解答】解:横轴的位置离交点越远则年份越多,纵轴的位置离交点越远则价格越高,所以甲比乙新,且甲比乙价格贵。
故选:D。
【名师点评】此题考查了学生通过观察统计图从统计图中获取信息的能力。
二.填空题
11.【考点】亿以上数的改写与近似.
【答案】126666000000,147。
【思路分析】根据整数的写法,从高位到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0;改写成用“万”作单位的数,就是把千位上的数进行四舍五入,再在数的后面写上“万”字;结果保留整数,就是将十分位上的数四舍五入到个位。
【解答】解:2021年增城区全区实现地区生产总值一千二百六十六亿六千六百万元,横线上的数写作126666000000。2021年增城区常住人口1466300人,横线上的数改写成用“万”作单位的数是147万人(结果保留整数)。
故答案为:126666000000,147。
【名师点评】本题主要考查整数的写法和求近似数,求近似数时要注意带计数单位。
12.【考点】求比值和化简比.
【答案】见试题解答内容
【思路分析】根据比的基本性质,:0.25的前、后项都乘8即可将此比化成最简整数比;根据比值的意义,比的前项除以后项的商就是比值。
【解答】解::0.25=3:2
=3:2
=3÷2
=1.5
答::0.25的最简整数比是3:2,比值是1.5。
故答案为:3:2,1.5。
【名师点评】此题是考查比的化简与求比值,属于基础知识,要掌握。
13.【考点】找一个数的倍数的方法;公因数和公倍数应用题;找一个数的因数的方法.
【答案】3,15;48。
【思路分析】(1)15以内,3的倍数有3、6、9、12、15。15的因数有1、3、5、15。找出既是3的倍数,又是15的因数即可解答。
(2)根据求最小公倍数的方法,求出16和12的最小公倍数,找出小于60人的倍数即可。
【解答】解:(1)3的倍数有3、6、9、12、15……。15的因数有1、3、5、1^既是3的倍数,又是15的因数,这个数是3或是15。
(2)16=2×2×2×2,12=2×2×3,16和12的最小公倍数是2×2×2×2×3=48;
48×2=96
96>60
48<60
六年级有48人。
故答案为:3,15;48。
【名师点评】本题考查公因数和公倍数的计算及应用。
14.【考点】圆柱的侧面积、表面积和体积;长方体和正方体的体积.
【答案】1000,100。
【思路分析】从图上可得:正方体的棱长是10dm,因为圆柱的底面积和正方体的底面积相同,所以根据正方形面积公式S=边长×边长,正方体的体积公式:V=棱长×棱长×棱长,将数据代入,即可得出答案。
【解答】解:10×10×10
=100×10
=1000(dm3)
10×10=100(dm2)
答:正方体的体积是1000dm3,圆柱的底面积是100dm2。
故答案为:1000,100。
【名师点评】本题考查学生对正方形面积和正方体体积的运用,要求学生熟练掌握公式。
15.【考点】小数除法.
【答案】用2.51×0.23验算,2.51和0.23都是两位数小数,则它们的积是4位小数,而5.98只有两位小数,所以是错的。(答案不唯一)
【思路分析】可以用商×除数=被除数的方法进行验算。
【解答】解:用2.51×0.23验算,2.51和0.23都是两位数小数,则它们的积是4位小数,而5.98只有两位小数,所以是错的。(答案不唯一)
故答案为:用2.51×0.23验算,2.51和0.23都是两位数小数,则它们的积是4位小数,而5.98只有两位小数,所以是错的。(答案不唯一)
【名师点评】本题主要考查了通过不计算判断小数除法算式是否正确,可以通过用乘法验算的方法进行判定。
16.【考点】小数的读写、意义及分类;小数的近似数及其求法.
【答案】104000030.6,一亿零四百万零三十点六,10400万。
【思路分析】小数的写法:整数部分按照整数的写法来写(整数部分是零的写作“0”),小数点点在个位的右下角,小数部分顺次写出每一个数位上的数字;
小数的读法:整数部分按整数的读法来读,小数点读作点,小数部分要依次读出每个数字;
省略“万”后面的尾数求它的近似数,要把万位的下一位千位上的数进行四舍五入,再在数的后面带上“万”字;
由此求解。
【解答】解:一个数由1个亿、4个百万、3个十、6个0.1组成,这个数写作104000030.6,读作一亿零四百万零三十点六,省略万位后的尾数得到10400万。
故答案为:104000030.6,一亿零四百万零三十点六,10400万。
【名师点评】本题主要考查小数读、写和求近似数,注意找清楚每一个数位上数字是多少。
17.【考点】小面积单位间的进率及单位换算;体积、容积进率及单位换算;时、分、秒及其关系、单位换算与计算.
【答案】40,8300,2.5。
【思路分析】低级单位平方分米化高级单位平方米除以进率100;
高级单位升化低级单位毫升乘进率1000;
把30分除以进率60化成0.5时,再加2时。
【解答】解:
4000dm2=40m2 8.3L=8300mL 2时30分=2.5时
故答案为:40,8300,2.5。
【名师点评】单位换算首先要弄清是由高级单位化低级单位还是由低级单位化高级单位,其次记住单位间的进率;由高级单位化低级单位乘进率,由低级单位化高级单位除以进率。
18.【考点】存款利息与纳税相关问题.
【答案】12000。
【思路分析】把1.5万元看作单位“1”,1.5万元=15000元,按规定应缴纳20%的个人所得税后剩余的钱就是实际得到的奖金,列式为15000×(1﹣20%),解决问题。
【解答】解:15000×(1﹣20%)
=15000×80%
=12000(元)
答:张叔叔实际得到奖金12000元。
故答案为:12000。
【名师点评】或者用总钱数扣除20%的个人所得税,列式为15000﹣15000×20%。
19.【考点】百分数的实际应用.
【答案】3.6
【思路分析】根据题意:把去年“五一”劳动节当天,公园的游客数量看作单位“1”,根据已知条件可知:今年“五一”当天的游客数量是去年的1+80%=180%,然后根据百分数乘法的意义,求一个数的百分之几用乘法计算,解答此题。
【解答】解:2×(1+80%)
=2×1.8
=3.6(万人次)
答:今年“五一”当天的游客数量是3.6万人次。
故答案为:3.6。
【名师点评】完成本题的关键是熟记关系式:比单位“1”多的公式为:单位“1”的量×(1+百分之几)。
20.【考点】分数乘法应用题.
【答案】12。
【思路分析】把爷爷的年龄看作单位“1”,用爷爷的年龄,可以计算出爸爸的年龄,再用爸爸的年龄乘,可以计算出我的年龄。
【解答】解:
=12(岁)
答:我今年12岁。
故答案为:12。
【名师点评】本题考查分数乘法应用题,解题关键是先找出题目中的单位“1”是哪个量,再根据一个数乘分数的意义,列式计算。
21.【考点】整数、小数复合应用题.
【答案】5。
【思路分析】根据总价÷单价=数量,代入数值即可求出可以买多少本,结尾用去尾法保留整数。
【解答】解:100÷18.5≈5(本)
答:他最多可以买5本。
故答案为:5。
【名师点评】本题主要考查了小数除法的实际应用,注意结尾用去尾法保留整数。
22.【考点】圆锥的体积.
【答案】圆锥体;12.56。
【思路分析】根据题意可知,以直角三角形以3cm的直角边所在直线为轴旋转一周,可以得到一个底面半径是2厘米,高是3厘米的圆锥,根据圆锥的体积=底面积×高÷3,把数据代入公式解答。
【解答】解:3.14×2×2×3÷3
=12.56×3÷3
=12.56(立方厘米)
答:可得到一个圆锥体,体积是12.56cm3。
故答案为:圆锥体;12.56。
【名师点评】此题考查的目的是理解掌握圆锥的特征,以及圆锥体积公式的灵活运用,关键是熟记公式。
三.判断题
23.【考点】圆柱的展开图.
【答案】×
【思路分析】因为将圆柱沿高展开后得到一个长方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高,由此再根据“一个圆柱的侧面展开是一个正方形,”知道圆柱的底面周长与圆柱的高相等。
【解答】解:一个底面周长和高相等的圆柱,侧面沿高展开后得到一个正方形。原题说法错误。
故答案为:×。
【名师点评】此题主要考查了圆柱与圆柱的侧面展开图之间的关系。
24.【考点】轴对称图形的辨识.
【答案】见试题解答内容
【思路分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;进行判断即可.
【解答】解:根据轴对称图形的意义可知:正方形、长方形、圆都是轴对称图形,
而三角形和梯形不一定是轴对称图形,只有等腰三角形和等腰梯形是轴对称图形;
故答案为:×.
【名师点评】此题考查了轴对称图形的意义,判断轴对称图形的关键是寻找对称轴,看图形对折后两部分是否完全重合.
25.【考点】百分数的实际应用.
【答案】见试题解答内容
【思路分析】含盐百分比是指含盐的重量占盐水总重量的百分之几,求出后来加入的盐水的含盐百分比然后与30%比较即可.
【解答】解:6÷(6+14)×100%,
=6÷20×100%,
=30%;
加入的盐水的含盐百分比30%,与原来相同,所以后来的含盐百分比也是30%.
故答案为:√.
【名师点评】本题关键是理解含盐百分比,找出其计算的方法,只要加入的盐水的含盐百分比也是30%,那么后来的盐水的含盐百分比就是30%.
26.【考点】百分数的实际应用.
【答案】见试题解答内容
【思路分析】第一个单位“1”是原价,提价后的价格就是原价的1+10%;第二个10%的单位“1”是提价后的价格,现价是提价后价格的1﹣10%,求出现价再与原价比较即可.
【解答】解:设原价是1,则提价后的价格是:
1×(1+10%)=110%;
现价是:110%×(1﹣10%)
=110%×90%,
=99%;
99%<1,即现价低于原价.
故答案为:√.
【名师点评】解答此题的关键是分清两个单位“1”的区别,找清各自以谁为标准,再把数据设出,根据数量关系求解.
27.【考点】事件的确定性与不确定性.
【答案】×
【思路分析】事件可分为确定事件和不确定事件,确定事件可分为必然事件和不可能事件,不确定事件又称为随机事件。
【解答】解:三天后会不会下雪是未确定事件,所以不能用一定描述,应说三天后可能会下雪。原题说法错误。
故答案为:×。
【名师点评】此题应根据可能性的大小进行分析、解答。
28.【考点】植树问题.
【答案】√
【思路分析】一根木头锯4段,需要锯(4﹣1)次,由此计算出平均每次需要时间,然后计算锯6段的时间,由此解答本题。
【解答】解:12÷(4﹣1)
=12÷3
=4(分)
4×(6﹣1)
=4×5
=20(分)
答:如果锯6段,那么要用20分。
本题说法正确。
故答案为:√。
【名师点评】解决本题的关键是找出题中数量关系。
四.计算题
29.【考点】分数乘除混合运算;分数的四则混合运算;分数除法.
【答案】2.1;28;36;2.58;;13.4;9;;。
【思路分析】计算小数加减法,要相同数位对齐,从低位算起;
小数除法的计算,根据商不变的性质,先移动除数的小数点使它变成整数,再根据除数是整数的除法算出商;
分数乘法的计算法则,分子相乘的积做分子,分母相乘的积做分母;
分数除法的计算法则,除以一个不为0的数等于乘这个数的倒数;
异分母分数相加减,要先通分,化成同分母分数后再计算。
【解答】解:
8.42.1 70×40%=28 3036
5.7﹣3.12=2.58 1 7.4+6=13.4
3.6÷0.4=9
【名师点评】本题解题关键是熟练掌握分数、小数四则运算的计算方法。
30.【考点】解比例.
【答案】(1)x=21;
(2)x。
【思路分析】(1)根据比例的基本性质的性质,把原式化为4x=3×28,然后方程的两边同时除以4求解;
(2)根据比例的基本性质的性质,把原式化为10x,然后方程的两边同时除以10求解。
【解答】解:(1)
4x=3×28
4x÷4=3×28÷4
x=21
(2)x::10
10x
10x÷1010
x
【名师点评】本题考查解方程和解比例,解题的关键是掌握等式的性质与比例的基本性质:方程两边同时加上或减去相同的数,等式仍然成立;方程两边同时乘(或除以)相同的数(0除外),等式仍然成立;两个外项的积等于两个内项的积。
31.【考点】运算定律与简便运算.
【答案】(1)4.5;
(2);
(3)0;
(4)。
【思路分析】(1)先算除法,再算减法;
(2)根据乘法分配律进行计算;
(3)先算除法,再根据减法的性质进行计算;
(4)先算小括号里面的减法,再算中括号里面的除法,最后算括号外面的乘法。
【解答】解:(1)20.5﹣6
=20.5﹣16
=4.5
(2)12
=()
(3)2
=2
=2﹣()
=2﹣2
=0
(4)[]
[]
【名师点评】考查了运算定律与简便运算,四则混合运算。注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
五.操作题(共1小题)
32.【考点】作旋转一定角度后的图形;图形的放大与缩小.
【答案】(1)~(3);
(4)75。
【思路分析】(1)根据旋转的特征,长方形绕点A顺时针旋转90°,点A的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形①。
(2)画圆时,“圆心定位置,半径定大小”,以确定的点O为圆心,以3厘米为半径画圆即可。
(3)根据图形放大与缩小的意义,把长方形的长、宽均缩小到原来的,所得到的图形就是原长方形按1:2缩小后的图形②。
(4)根据长方形的面积计算公式“S=ab”分别计算出原来长方形的面积、缩小后长方形的面积,再用原长方形面积与缩小后长方形面积的差除以原长方形的面积。
【解答】解:(1)~(3)画图如下:
(4)(4×2﹣2×1)÷(4×2)
=(8﹣2)÷8
=6÷8
=0.75
=75%
答:缩小后的长方形的面积比原来的长方形面积少75%。
故答案为:75。
【名师点评】此题考查了作旋转一定度数后的图形、图形的放大与缩小、画圆、百分数的应用。
六.应用题
33.【考点】分数四则复合应用题.
【答案】48页。
【思路分析】根据乘数的意义,第一天看的页数=全书的页数;第二天看的页数=余下的页数;余下的页数=全书页数﹣第一天看的页数;第一天的页数+第二天的页数=两天一共看的页数。
【解答】解:120(120﹣120)
=24+(120﹣24)
=24+96
=24+24
=48(页)
答:两天一共看了48页。
【名师点评】分析题目数量之间的关系,根据数量之间的关系列出数量关系式,根据数量关系式解决问题。
34.【考点】简单的行程问题.
【答案】120千米。
【思路分析】根据题意,这道题的等量关系是:去时的速度×时间=返回时的速度×时间,根据这个等量关系,列方程解答。
【解答】解:设原来每小时行x千米。
6x=(x﹣5)×8
6x=8x﹣40
8x﹣6x=40
2x=40
x=20
20×6=120(千米)
答:甲城到乙城的路程有120千米。
【名师点评】本题考查行程问题的解题方法,用方程解答比较简便,解题关键是找出题目中的等量关系:去时的速度×时间=返回时的速度×时间,列方程解答。
35.【考点】逆推问题.
【答案】100个。
【思路分析】根据题意,把当天桃子总数看作单位“1”,则第9天摘之前树上的桃子数是10÷(1),同理,第8天摘之前树上的桃子是第9天桃子总数(第8天剩下的桃子数)的(1),依此类推,用除法求出桃子总数即可。
【解答】解:10÷(1)÷(1)÷……÷(1)
=10
=10×2
=10×10
=100(个)
答:树上原来有100个桃子。
【名师点评】本题主要考查逆推问题,关键求摘之前树上桃子的数量。
36.【考点】分数四则复合应用题.
【答案】15顶。
【思路分析】先依据顶数=布的长度÷每顶帽子用布长度,求出可制作帽子顶数,并把此看作单位“1”,运用分数乘法意义即可解答。
【解答】解:8
=20
=15(顶)
答:送给养老院15顶帽子。
【名师点评】分数乘法意义是解答本题的依据,关键是求出制作帽子顶数。
37.【考点】鸡兔同笼.
【答案】见试题解答内容
【思路分析】假设全部为跳棋,一共有:26×6=156人,比实际多了156﹣120=36人,这是因为我们把下象棋的人当作了下跳棋的人,每副多算了:6﹣2=4人;所以有象棋:36÷4=9(副),那么跳棋就为:26﹣9=17(副);据此解答.
【解答】解:假设全部为跳棋,
象棋:(26×6﹣120)÷(6﹣2)
=36÷4
=9(副)
跳棋:26﹣9=17(副)
答:象棋有9副,跳棋有17副.
【名师点评】解决鸡兔同笼问题往往用假设法解答,有些应用题中有两个或两个以上的未知量,思考问题时,可以假设要求的两个或两个以上的未知量相等,或假设它们为同一种量,然后按照题中的已知条件进行推算,如果数量上出现矛盾,可适当调整,以求出正确的结果.
38.【考点】正、反比例应用题.
【答案】32名。
【思路分析】根据每60名同学聘请2名讲解员作介绍,那么每(60÷2)名同学聘请1名讲解员作介绍(一定),学生人数与讲解员成正比例;设全校960名同学参观,需要聘请x名讲解员,即可列出比例解答。
【解答】解:设全校960名同学参观,需要聘请x名讲解员。
960:x=60:2
60x=960×2
60x=1920
x=32
答:需要聘请32名讲解员。
【名师点评】确定正、反比例是解答关键。
21世纪教育网(www.21cnjy.com)
同课章节目录
