(小升初开学分班考)小升初开学分班考摸底押题卷-2025年秋六年级数学人教版(含答案解析)
文档属性
| 名称 | (小升初开学分班考)小升初开学分班考摸底押题卷-2025年秋六年级数学人教版(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 182.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 23:08:09 | ||
图片预览



文档简介
/ 让学习更有效 小升初备考 | 数学学科
2025年秋六年级数学小升初开学分班考摸底押题卷(人教版)
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题
1.电梯上升记为正,下降记为负。从一楼开始,电梯经过如下四次运动:+11层,﹣5层,﹣7层,+15层。现在电梯停在( )楼。
A.15 B.1 C.14 D.﹣1
2.设“●”、“▲”、“■”表示三种不同的物体,用天平比较它们的大小,两次情况如图所示,那么三种物品的重量从大到小的顺序排列为( )
A.■●▲ B.■▲● C.▲●■ D.▲■●
3.把一个三角形按比例放大或缩小后,( )不变。
A.边长 B.内角大小 C.周长 D.面积
4.在2:3中,如果前项增加10,要使比值不变,后项应增加( )
A.12 B.13 C.14 D.15
5.安安想知道花都区2020年5月份整月的气温变化情况,她要搜集的数据是( )
A.2020年各个季度平均气温 B.2020年各月平均气温
C.2020年5月每天的平均气温 D.2020年5月1日的各个时刻的气温
6.吸烟不仅有害健康而且浪费钱财。如果一位吸烟者每天吸一包28元的香烟,那么他每年花在吸烟上的钱大约是( )元
A.20000 B.10000 C.8000 D.5000
7.东东、青青、芳芳三人分一包糖果,准备按3:2:5或1:2:3来分配,两种分法中( )分得的一样多。
A.东东 B.青青 C.芳芳 D.无法确定
8.如图,以图书馆为观察点,游乐场在( )
A.东偏南30° B.南偏东30° C.西偏北30° D.北偏西30°
9.六(3)班同学的位置设了8列,每列位置一样多,第八列最后一名同学的位置是(8,6),则六(3)班共有同学( )
A.56人 B.48人 C.64人
10.用5个大小相等的小正方体搭成下面三个立体图形,从( )看这三个立体图形所看到的形状是完全一样的.
A. B. C.
二.填空题
11.六(1)班同学参加体育达标检测,6人未达标,达标率为88%。六(1)班有学生 人。
12.把2.5升油,倒入容积是300毫升的瓶子里,至少需要 个这样的瓶子。
13.把25克盐溶解在100克水中,盐与水的比是 ,盐占盐水的 %。
14.如图有 条对称轴,如果每个圆的周长是25.12cm,长方形的面积是 cm2.
15.一幅地图的比例尺是1:3000000;图上距离3cm的距离表示实际 km的距离,如果实际距离是150km,在这幅图上应画 cm.
16.一张正方形桌坐4个人(每个圆圈表示1个人),两张桌子排在一起能坐6个人,按照这样的规律,8张桌子排在一起,能坐 个人。
17.一本故事书有100页,小明每天看12页,看了a天,还剩 页没看。当a=7时,还剩 页没看。
18.一个等腰三角形的顶角是50°,它的其中一个底角是 °.
19.在一幅地图上,图上距离3厘米表示实际距离120米,这幅地图的比例尺是 。
20.把87%、、0.86、0.8这四个数,按从小到大的顺序进行排列是: < <_______ <
21.跑同一段路,小兰跑完全程需要5小时,小宁跑完全程需要三小时,小兰和小宁速度的最简比是 。
22.商场有香蕉a千克,比葡萄的4倍少20千克,则葡萄有 千克。如果香蕉有100千克,则葡萄有 千克。
三.判断题
23.小麦的出粉率一定,小麦的总重量和面粉的重量成正比例关系. .
24.圆柱体的体积与圆锥体的体积比是3:1. .
25.在和之间只有一个最简真分数。
26.长方形、正方形、等腰三角形、直角梯形和圆都是轴对称图形。
27.如果n是自然数,那么2n+2一定是偶数. .
28.一个数的因数都比这个数的倍数小. .
四.计算题
29.直接写出得数。
305﹣199= 31×197≈ 510÷30= 0.22=
3.5×0.2=
30.解方程
(1)x:10: (2)7x+5×0.7=8.4
31.用你喜欢的方法计算。
12.7×99+12.7
五.操作题
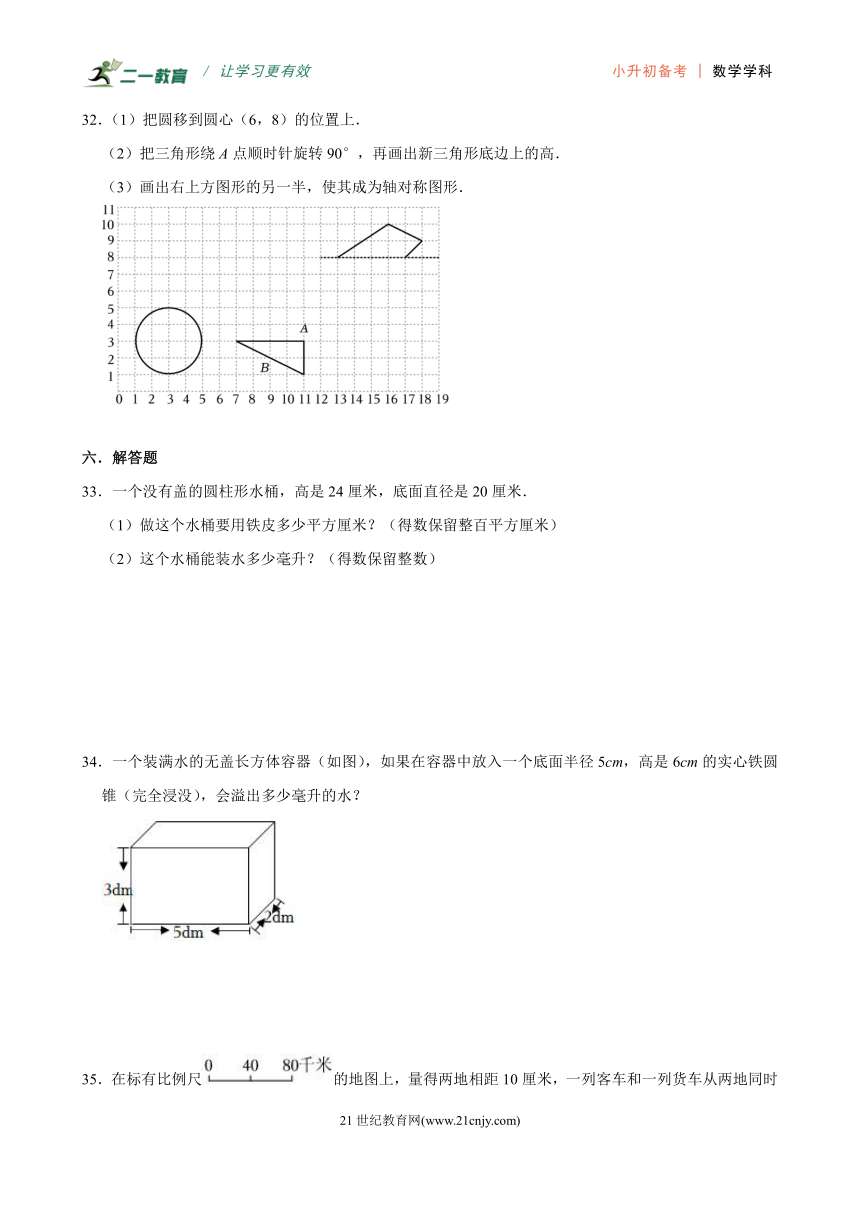
32.(1)把圆移到圆心(6,8)的位置上.
(2)把三角形绕A点顺时针旋转90°,再画出新三角形底边上的高.
(3)画出右上方图形的另一半,使其成为轴对称图形.
六.解答题
33.一个没有盖的圆柱形水桶,高是24厘米,底面直径是20厘米.
(1)做这个水桶要用铁皮多少平方厘米?(得数保留整百平方厘米)
(2)这个水桶能装水多少毫升?(得数保留整数)
34.一个装满水的无盖长方体容器(如图),如果在容器中放入一个底面半径5cm,高是6cm的实心铁圆锥(完全浸没),会溢出多少毫升的水?
35.在标有比例尺的地图上,量得两地相距10厘米,一列客车和一列货车从两地同时相向而行,客车每小时行60千米,货车每小时行40千米,两车经过多少小时相遇?
36.如图所示为一个棱长6厘米的正方体,从正方体的底面向内挖去一个最大的圆锥体,剩下的体积是多少立方厘米?
37.一幢教学楼的平面图上,量的楼长16厘米,宽7.2厘米.已知比例尺是1:250,这幢教学楼的实际面积是多少平方米?
38.一列客车和一列货车同时从两个城市相对开出,客车每小时行40千米,货车的速度是客车的,两车开出2.5小时后相遇,两城相距多少千米?
39.客车和货车分别从甲乙两站同时相向开出,5小时后相遇,相遇后两车仍按原速度前进,当他们相距196千米时,客车行了全程的,货车行了全程的80%.
(1)全程是多少千米?
(2)货车行完全程需要多少个小时?
参考答案及试题解析
一.选择题
1.【考点】负数的意义及其应用.
【答案】A
【思路分析】把数据相加,得出最后的数,然后根据“上升记为正,下降记为负”计算到达楼层即可。
【解答】解:+11﹣5﹣7+15=+14
1+14=15(楼)
答:现在电梯停在15楼。
故选:A。
【名师点评】此题主要考查正负数的意义,要熟练掌握。
2.【考点】简单的等量代换问题.
【答案】B
【思路分析】根据题目中的图形就可以得到一个不等关系:□>△,一个相等关系:2个圆=1个△,就可以得到三个物体的质量的大小.
【解答】解:由第一个图可知:■>▲,
由第二个图可知:2●=▲,
所以■>▲>●,
故选:B.
【名师点评】此题主要考查了一元一次不等式组的应用,读懂图中列出不等式关系式即可求解.
3.【考点】图形的放大与缩小.
【答案】B
【思路分析】缩小后和放大后的图形与原图形相比,形状相同、大小不相同,据此解答。
【解答】解:把一个三角形按比例放大或缩小后,内角大小不变,但是边长、周长和面积都变了。
故选:B。
【名师点评】本题主要考查图形的放大与缩小的特征。
4.【考点】比的性质.
【答案】D
【思路分析】如果前项增加10,变成12,相当于前项乘6,要使比值不变,那么后项应乘6,相当于增加3的5倍,是15。
【解答】解:10+2=12
3×(12÷2﹣1)
=3×5
=15
要使比值不变,那么后项应增加15。
故选:D。
【名师点评】此题考查了比的性质,要熟练掌握。
5.【考点】设计统计活动.
【答案】C
【思路分析】根据题意安安想知道花都区2020年5月份整月的气温变化情况,因此他要做的就是把5月份每天的平均气温都要搜集出来。
【解答】解:安安想知道花都区2020年5月份整月的气温变化情况,她要搜集的数据是2020年5月每天的平均气温。
故选:C。
【名师点评】本题考查了数据整理前必需要做好数据的收集。
6.【考点】数的估算.
【答案】B
【思路分析】根据题目中的数据,据整数乘法的估算方法:把相乘的因数看成最接近它的整十、整百数来算;28≈30,365≈370,所以与28×365≈11100,11100≈1000,据此选择即可。
【解答】解:28×365≈30×370≈10000(元)
故选:B。
【名师点评】此题考查了整数乘法的估算方法,注意把相乘的数看成最接近它的整十数和几百几十的数。
7.【考点】按比例分配应用题.
【答案】C
【思路分析】根据题意可知,这一包糖为单位“1”不变,只是分的份数不同,因此求出每个人两次分得这包糖的几分之几,分率一样的即可判断分得一样多。
【解答】解:东东:3÷(3+2+5),1÷(1+2+3),两次分得不一样多,不符合题意;
青青:2÷(3+2+5),2÷(1+2+3),两次分得不一样多,不符合题意;
芳芳:5÷(3+2+5),3÷(1+2+3),两次分得一样多,符合题意。
通过以上分析可知,芳芳两次分得糖果都是,也就是这包糖果的一半,一样多。
故选:C。
【名师点评】解答此题的关键明白不管怎么分,单位“1”始终不变。
8.【考点】用角度表示方向.
【答案】C
【思路分析】依据地图上的方向辨别方法,即“上北下南、左西右东”,以及图上标注的其他信息,即可进行解答.
【解答】解:如图,以图书馆为观察点,游乐场在西偏北30°;
故选:C。
【名师点评】此题主要考查地图上的方向辨别方法的灵活应用.
9.【考点】数对与位置.
【答案】B
【思路分析】根据“第八列最后一名同学的位置是(8,6),”知道此教室里一共坐了6行同学,又知道六(3)班同学的位置设了8列,由此根据整数乘法的意义,列数即可解答.
【解答】解:8×6=48(人);
答:六(3)班共有同学48人.
故选:B。
【名师点评】此题考查了数对的意义,即数对中的第一个数表示列数;数对中的第二个数表示行数.
10.【考点】从不同方向观察物体和几何体.
【答案】A
【思路分析】分别得到3个立体图形从正面、上面、侧面所看到的图形,找到其中形状是完全一样的即可.
【解答】解:从正面、上面、侧面所看到的图形如下:
观察图形,只有从正面看所看到的立体图形的形状是完全一样的.
故选:A.
【名师点评】此题考查了从不同方向观察物体和几何体,应注意小正方形的数目及位置.
二.填空题
11.【考点】百分率应用题.
【答案】50。
【思路分析】先明确达标率,即达标学生人数占全班总人数的百分之几,把全班人数看作单位“1”,达标率为88%,则未达标的人数占总人数的1﹣88%,然后再根据百分数除法的意义进行计算即可。
【解答】解:6÷(1﹣88%)
=6÷12%
=50(人)
答:六(1)班有学生50人。
故答案为:50。
【名师点评】解答此题应先判断出单位“1”,然后根据求一个数是另一个数的百分之几,用除法计算即可.
12.【考点】有余数的除法应用题.
【答案】9。
【思路分析】根据题意,也就是求2.5升(2500毫升)里面有几个300毫升,用除法计算。
【解答】解:2.5升=2500毫升
2500÷300≈9(瓶)
答:至少需要9个这样的瓶子。
故答案为:9。
【名师点评】此题考查有余数的除法应用题,解决此题的关键是:理解“进一法”的意义,即无论结果剩多少毫升,都要再多装1瓶。
13.【考点】比的意义;百分数的意义、读写及应用.
【答案】1:4,20。
【思路分析】盐与水的比是25:100,前项后项同时除以25,化简得1:4。那么盐占盐水的1÷(1+4)×100%,计算即可。
【解答】解:25:100=1:4
1÷(1+4)×100%
=0.2×100%
=20%
答:盐与水的比是1:4,盐占盐水的20%。
故答案为:1:4,20。
【名师点评】此题主要考查了比的意义和百分数的意义,要熟练掌握。
14.【考点】确定轴对称图形的对称轴条数及位置;圆、圆环的周长;圆、圆环的面积.
【答案】见试题解答内容
【思路分析】①根据轴对称图形的定义:一个图形沿一条直线对折,直线两旁的部分能够完全重合,则这个图形就是轴对称图形,这条直线就是这个图形的一条对称轴,据此即可解答.
②根据圆的直径是C÷π,求出圆的直径,然后根据长方形的面积公式解答即可.
【解答】解:
25.12÷3.14=8(厘米)
8×2=16(厘米)
8×16=128(平方厘米)
答:如图有 2条对称轴,如果每个圆的周长是25.12cm,长方形的面积是128cm2;
故答案为:2,128
【名师点评】此题主要考查如何确定轴对称图形的对称轴条数及位置以及圆的周长和长方形面积计算方法.
15.【考点】比例尺应用题.
【答案】见试题解答内容
【思路分析】(1)已知比例尺和图上距离,要求实际距离,应根据关系式:图上距离÷比例尺=实际距离,进行解答,列式为3.
(2)已知比例尺和实际距离,要求图上距离,应根据关系式:实际距离×比例尺=图上距离,进行解答,列式为15000000.
【解答】解:(1)3,
=3×3000000,
=9000000(cm),
=90(km);
答:图上距离3cm的距离表示实际90km的距离.
(2)150km=15000000cm,
150000005(cm).
答:实际距离是150km,在这幅图上应画5cm.
故答案为:90,5.
【名师点评】此题主要考查比例尺、图上距离、实际距离三者之间的数量关系:比例尺=图上距离÷实际距离,灵活变形列式解决问题.
16.【考点】数与形结合的规律.
【答案】18。
【思路分析】观察三个图形得到一张正方形桌子可坐4人,二张正方形桌子可坐(4+2×1)人,则每增加一个桌子就可多坐两个人,于是得到n张正方形桌子可坐[4+2(n﹣1)]人。
【解答】解:由分析可得:
4+2×(8﹣1)
=4+2×7
=4+14
=18(人)
答:8张桌子排在一起,能坐18个人。
故答案为:18。
【名师点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力。
17.【考点】用字母表示数.
【答案】(100﹣12a);16。
【思路分析】根据题干,每天看12页,看了a天,则已经看了12a页,用总页数减去已经看完的页数,即可得到剩下的页数,再把a=7代入计算即可解答问题。
【解答】解:还剩下(100﹣12a)页
当a=7时
100﹣12×7
=100﹣84
=16(页)
答:还剩(100﹣12a)页没看,当a=7时,还剩16页没看。
故答案为:(100﹣12a);16。
【名师点评】做这类用字母表示数的题目时,解题关键是根据已知条件,把未知的数用字母正确的表示出来,然后根据题意列式计算即可得解。
18.【考点】三角形的内角和;等腰三角形与等边三角形.
【答案】见试题解答内容
【思路分析】因为等腰三角形的两个底角相等,三角形的内角和是180度,所以底角的度数=(180°﹣顶角)÷2,代入数据计算即可.
【解答】解:(180°﹣50°)÷2
=130°÷2
=65°;
答:它的其中一个底角是65°.
故答案为:65.
【名师点评】此题根据三角形内角和等于180度和等腰三角形的特点进行解答.
19.【考点】比例尺.
【答案】1:4000。
【思路分析】根据比例尺=图上距离:实际距离,代入数据解答即可。
【解答】解:3cm:120m
=3cm:12000cm
=1:4000
答:这幅地图的比例尺是1:4000。
故答案为:1:4000。
【名师点评】解答此题的关键是掌握比例尺=图上距离:实际距离这个公式。
20.【考点】小数大小的比较.
【答案】0.86,0.87,,0.8。
【思路分析】首先根据小数、分数和百分数之间的互化的方法,把其中的分数和百分数都化成小数,然后根据小数大小比较的方法,把各数按从小到大的顺序排列即可。
【解答】解:87%=0.87
0.875
0.80.8777......
0.86<0.870.8
故答案为:0.86,0.87,,0.8。
【名师点评】此题主要考查了小数、分数和百分数之间的互化的方法,以及小数大小比较的方法,要熟练掌握。
21.【考点】比的意义.
【答案】3:5。
【思路分析】把路的总米数看作单位“1”,根据小兰、小宁跑完分别需要的小时数,先分别求出小兰、小宁的速度,进而写比并化简比。
【解答】解:(1÷5):(1÷3)
:
=3:5
答:小兰和小宁速度的最简比是3:5。
故答案为:3:5。
【名师点评】本题主要考查了比的意义,用到速度=路程÷时间。
22.【考点】用字母表示数.
【答案】(a+20)÷4,30。
【思路分析】用香蕉得千克数加20千克,再除以4,即可得葡萄的千克数。把香蕉的千克数代入,计算即可。
【解答】解:(a+20)÷4
答:葡萄有(a+20)÷4千克。
(100+20)÷4
=120÷4
=30(千克)
答:如果香蕉有100千克,则葡萄有30千克。
故答案为:(a+20)÷4,30。
【名师点评】本题主要考查了用字母表示数和含字母式子求值,要分清数量关系。
三.判断题
23.【考点】正比例和反比例的意义.
【答案】见试题解答内容
【思路分析】判断小麦的总重量和面粉的重量是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果不是比值一定或比值不一定,就不成正比例.
【解答】解:面粉的重量÷小麦的总重量×100%=小麦的出粉率(一定),是比值一定,小麦的总重量和面粉的重量成正比例.
故判断为:正确.
【名师点评】此题属于辨识成正比例的量,就看这两种量是否是对应的比值一定,再做出判断.
24.【考点】圆柱的侧面积、表面积和体积;圆锥的体积.
【答案】×
【思路分析】圆柱的体积=底面积×高,圆锥的体积底面积×高,当底面积与高相等时,圆柱的体积与圆锥的体积之比是3:1,由此即可进行判断.
【解答】解:根据圆柱与圆锥的体积公式可知:当底面积与高相等时,圆柱的体积与圆锥的体积之比是3:1,
原题中没有说“等底等高”,所以原题说法错误.
故答案为:×.
【名师点评】此题考查了等底等高的圆柱与圆锥体积的倍数关系,这里要注意数学语言的严密性.
25.【考点】分数大小的比较.
【答案】×
【思路分析】根据分数的大小比较方法,大于而小于,分母为5的真分数只有一个;但是根据分数的基本性质,把这两个分数的分子、分母同时乘、同时乘3、4、5……,这两个分数之间的分数也随之增加,所以这两个分数之间有无数个。据此判断。
【解答】解:在和之间只有一个最简真分数有无数个,所以原题说法错误。
故答案为:×。
【名师点评】两个小数之间有无数个小数,两个分数之间也有无数个分数。
26.【考点】轴对称图形的辨识.
【答案】×
【思路分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;进行判断即可。
【解答】解:长方形、正方形、等腰三角形和圆都是轴对称图形,直角梯形不是轴对称图形,故原题说法错误。
故答案为:×。
【名师点评】此题考查了轴对称图形的意义,判断轴对称图形的关键是寻找对称轴,看图形对折后两部分是否完全重合。
27.【考点】用字母表示数;奇数与偶数的初步认识.
【答案】√
【思路分析】在自然数中,能被2整除的数叫作偶数,n为自然数,2n+2能被2整除,所以2n+2为偶数.
【解答】解:2n+2=2(n+1),
2(n+1)÷2=(n+1),
所以2n+2为偶数,
故答案为:√.
【名师点评】此题主要考查的是偶数的含义.
28.【考点】因数和倍数的意义.
【答案】见试题解答内容
【思路分析】一个数既是它本身的最小倍数,又是它本身的最大因数.如:5的最小倍数是5,最大因数也是5.由此即可解答.
【解答】解:因为一数既是它本身的最小倍数,又是它本身的最大因数,所以此题干不正确;
故答案为:×.
【名师点评】此题重点是考察因数和倍数的意义,要知道一数既是它本身的最小倍数,又是它本身的最大因数.
四.计算题
29.【考点】求比值和化简比;千以内加减法;数的估算;小数乘法;分数的加法和减法;分数乘法.
【答案】106;0;6000;17;0.04;0.7;;2;;25。
【思路分析】根据整数加减乘除法、小数乘除法、分数加减乘除法的计算方法计算即可;
估算时,把数看作与之接近的整十数来估算;
求比值,用比的前项除以后项即可。
【解答】解:
305﹣199=106 0 31×197≈6000 510÷30=17 0.22=0.04
3.5×0.2=0.7 2 25
【名师点评】本题考查口算,注意计算的准确性。
30.【考点】分数方程求解;解比例.
【答案】x=5;x=0.7。
【思路分析】(1)根据比例的基本性质,把原式化为x=10,然后方程的两边同时除以求解。
(2)先计算5×0.7=3.5,根据等式的性质,方程的两边同时减去3.5,然后方程的两边同时除以7求解。
【解答】解:(1)x:10:
x=10
x10
x=5
(2)7x+5×0.7=8.4
7x+3.5=8.4
7x+3.5﹣3.5=8.4﹣3.5
7x=4.9
7x÷7=4.9÷7
x=0.7
【名师点评】本题考查解方程和解比例,解题的关键是掌握等式的性质与比例的基本性质:方程两边同时加上或减去相同的数,等式仍然成立;方程两边同时乘(或除以)相同的数(0除外),等式仍然成立;两个外项的积等于两个内项的积。
31.【考点】分数的四则混合运算;分数的简便计算(运算定律的分数应用);小数乘法(推广整数乘法运算定律).
【答案】1270;21;4;20.2。
【思路分析】按照乘法分配律计算;
按照乘法分配律计算;
按照加法交换律以及减法的性质计算;
先算小括号里面的除法,再算小括号里面的加法,最后算减法。
【解答】解:12.7×99+12.7
=12.7×(99+1)
=12.7×100
=1270
=3636
=27﹣6
=21
=4()
=5﹣1
=4
=28.8﹣(7.6+1)
=28.8﹣8.6
=20.2
【名师点评】本题考查了四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
五.操作题
32.【考点】作平移后的图形;作旋转一定角度后的图形;数对与位置;作三角形的高;作轴对称图形.
【答案】见试题解答内容
【思路分析】(1)根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,即可把圆心移到(6,8)的位置上.
(2)根据旋转的特征,三角形绕点A顺时针旋转90°,点A的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形.这是一直角三角形,一条直角边是以另一条直角边为底的高,只需画出斜边上的高即可,过斜边所对角的顶点作斜边的垂直线段就是斜边上的高.
(3)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的下边画出上图的关键对称点,依次连接即可.
【解答】解:(1)把圆移到圆心(6,8)的位置上(图中红色部分).
(2)把三角形绕A点顺时针旋转90°(图中绿色部分),再画出新三角形底边上的高(图中虚线部分).
(3)画出右上方图形的另一半,使其成为轴对称图形(图中蓝色部分).
【名师点评】此题考查的知识有:数对与位置,作旋转一定度数后的图形、作三角形的高、作轴对称图形等.
六.解答题
33.【考点】关于圆柱的应用题.
【答案】见试题解答内容
【思路分析】(1)先根据水桶的底面直径依次求出半径和底面面积,然后再根据直径和高求出水桶的侧面积,用底面面积加上侧面积即可.
(2)根据已求出的底面面积(314平方厘米)和已知高(24厘米),底面积×高=容积.
【解答】解:(1)3.143.14×20×24,
=314+1507.2,
=1821.2(平方厘米),
≈1900平方厘米.
(2)(3.14)×24,
=314×24,
=7536(毫升).
答:做这个水桶需要铁皮1900平方厘米;这个水桶能装水7536毫升.
【名师点评】此题主要考查圆柱体的体积计算公式:V=πr2h和表面积,解答时一定要注意分清题目中条件,灵活解答.
34.【考点】圆锥的体积.
【答案】157毫升。
【思路分析】由题意可知,把这个圆锥放入容器中,溢出水的体积就等于这个圆锥的体积,根据圆锥的体积公式:Vπr2h,把数据代入公式解答。
【解答】解:3.14×52×6
3.14×25×6
=157(立方厘米)
157立方厘米=157毫升
答:会溢出157毫升的水。
【名师点评】此题主要考查圆锥体积公式的灵活运用,关键是熟记公式。
35.【考点】比例尺应用题.
【答案】4小时。
【思路分析】由线段比例尺可知1厘米代表40千米,量得两地间相距10厘米,也就是10个40千米,用乘法求出两地的路程,进而根据“路程÷速度之和=相遇时间”,代入数值,解答即可。
【解答】解:10×40=400(千米)
400÷(60+40)
=400÷100
=4(小时)
答:两车经过4小时相遇。
【名师点评】此题主要考查利用线段比例尺求出实际距离的方法,再根据路程、相遇时间和速度之和三者之间的关系解答。
36.【考点】简单的立方体切拼问题;长方体和正方体的体积;圆锥的体积.
【答案】见试题解答内容
【思路分析】剩下的体积就是这个棱长为6厘米的正方体的体积与高为6厘米的圆锥的体积之差,由此只要求得圆锥的底面半径即可解决问题:圆锥的底面在正方体的底面上,根据正方形内最大圆的特点可知:圆锥的底面半径为6÷2=3厘米.
【解答】解:6×6×63.146,
=2163.14×9×6,
=216﹣56.52,
=159.48(立方厘米),
答:剩下部分的体积是159.48立方厘米.
【名师点评】此题考查了正方体与圆锥的体积公式的灵活应用,这里正确得出正方体内最大的圆锥的底面半径与高是解决此类问题的关键.
37.【考点】图上距离与实际距离的换算(比例尺的应用).
【答案】见试题解答内容
【思路分析】图上距离和比例尺已知,先依据“实际距离=图上距离÷比例尺”分别求出长和宽的实际距离,进而利用长方形的面积公式即可求解.
【解答】解:164000(厘米)=40(米)
7.21800(厘米)=18(米)
40×18=720(平方米)
答:这幢教学楼的实际面积是720平方米.
【名师点评】分别求出长和宽的实际距离,是解答本题的关键.
38.【考点】相遇问题.
【答案】见试题解答内容
【思路分析】已知客车每小时行40千米,货车的速度是客车的,根据求一个数的几分之几是多少用乘法计算,可求出货车的速度,再根据路程=速度和×时间,可求出两地之间的路程,据此解答.
【解答】解:(40+40)×2.5
=(40+32)×2.5
=72×2.5
=180(千米)
答:两城相距180千米.
【名师点评】本题的重点是先求出货车的速度,进而根据路程=速度和×时间,可求出两地之间的路程.
39.【考点】简单的行程问题;分数、百分数复合应用题.
【答案】见试题解答内容
【思路分析】(1)根据题意,客车行了全程的,货车行了全程的80%,可知两车是相遇后又分开196千米,因此全程是196÷(80%﹣1),计算即可;
(2)客车、货车的速度比为:80%=3:4,则货车速度为:(490÷5)56(千米),那么货车行完全程需要的时间是:490÷56,计算即可.
【解答】解:(1)196÷(80%﹣1),
=196÷(0.6+0.8﹣1),
=196÷0.4,
=490(千米);
答:全程是490千米.
(2)客货速度比为:
:80%=3:4;
则货车速度为:
(490÷5),
=98,
=56(千米);
货车行完全程需要的时间是:
490÷56=8(小时).
答:货车行完全程需要8小时.
【名师点评】此题在解答第二问时,关键是求出客、货两车的速度比,进而求出货车速度,根据货车的速度求得货车行完全程需要的时间.
21世纪教育网(www.21cnjy.com)
2025年秋六年级数学小升初开学分班考摸底押题卷(人教版)
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题
1.电梯上升记为正,下降记为负。从一楼开始,电梯经过如下四次运动:+11层,﹣5层,﹣7层,+15层。现在电梯停在( )楼。
A.15 B.1 C.14 D.﹣1
2.设“●”、“▲”、“■”表示三种不同的物体,用天平比较它们的大小,两次情况如图所示,那么三种物品的重量从大到小的顺序排列为( )
A.■●▲ B.■▲● C.▲●■ D.▲■●
3.把一个三角形按比例放大或缩小后,( )不变。
A.边长 B.内角大小 C.周长 D.面积
4.在2:3中,如果前项增加10,要使比值不变,后项应增加( )
A.12 B.13 C.14 D.15
5.安安想知道花都区2020年5月份整月的气温变化情况,她要搜集的数据是( )
A.2020年各个季度平均气温 B.2020年各月平均气温
C.2020年5月每天的平均气温 D.2020年5月1日的各个时刻的气温
6.吸烟不仅有害健康而且浪费钱财。如果一位吸烟者每天吸一包28元的香烟,那么他每年花在吸烟上的钱大约是( )元
A.20000 B.10000 C.8000 D.5000
7.东东、青青、芳芳三人分一包糖果,准备按3:2:5或1:2:3来分配,两种分法中( )分得的一样多。
A.东东 B.青青 C.芳芳 D.无法确定
8.如图,以图书馆为观察点,游乐场在( )
A.东偏南30° B.南偏东30° C.西偏北30° D.北偏西30°
9.六(3)班同学的位置设了8列,每列位置一样多,第八列最后一名同学的位置是(8,6),则六(3)班共有同学( )
A.56人 B.48人 C.64人
10.用5个大小相等的小正方体搭成下面三个立体图形,从( )看这三个立体图形所看到的形状是完全一样的.
A. B. C.
二.填空题
11.六(1)班同学参加体育达标检测,6人未达标,达标率为88%。六(1)班有学生 人。
12.把2.5升油,倒入容积是300毫升的瓶子里,至少需要 个这样的瓶子。
13.把25克盐溶解在100克水中,盐与水的比是 ,盐占盐水的 %。
14.如图有 条对称轴,如果每个圆的周长是25.12cm,长方形的面积是 cm2.
15.一幅地图的比例尺是1:3000000;图上距离3cm的距离表示实际 km的距离,如果实际距离是150km,在这幅图上应画 cm.
16.一张正方形桌坐4个人(每个圆圈表示1个人),两张桌子排在一起能坐6个人,按照这样的规律,8张桌子排在一起,能坐 个人。
17.一本故事书有100页,小明每天看12页,看了a天,还剩 页没看。当a=7时,还剩 页没看。
18.一个等腰三角形的顶角是50°,它的其中一个底角是 °.
19.在一幅地图上,图上距离3厘米表示实际距离120米,这幅地图的比例尺是 。
20.把87%、、0.86、0.8这四个数,按从小到大的顺序进行排列是: < <_______ <
21.跑同一段路,小兰跑完全程需要5小时,小宁跑完全程需要三小时,小兰和小宁速度的最简比是 。
22.商场有香蕉a千克,比葡萄的4倍少20千克,则葡萄有 千克。如果香蕉有100千克,则葡萄有 千克。
三.判断题
23.小麦的出粉率一定,小麦的总重量和面粉的重量成正比例关系. .
24.圆柱体的体积与圆锥体的体积比是3:1. .
25.在和之间只有一个最简真分数。
26.长方形、正方形、等腰三角形、直角梯形和圆都是轴对称图形。
27.如果n是自然数,那么2n+2一定是偶数. .
28.一个数的因数都比这个数的倍数小. .
四.计算题
29.直接写出得数。
305﹣199= 31×197≈ 510÷30= 0.22=
3.5×0.2=
30.解方程
(1)x:10: (2)7x+5×0.7=8.4
31.用你喜欢的方法计算。
12.7×99+12.7
五.操作题
32.(1)把圆移到圆心(6,8)的位置上.
(2)把三角形绕A点顺时针旋转90°,再画出新三角形底边上的高.
(3)画出右上方图形的另一半,使其成为轴对称图形.
六.解答题
33.一个没有盖的圆柱形水桶,高是24厘米,底面直径是20厘米.
(1)做这个水桶要用铁皮多少平方厘米?(得数保留整百平方厘米)
(2)这个水桶能装水多少毫升?(得数保留整数)
34.一个装满水的无盖长方体容器(如图),如果在容器中放入一个底面半径5cm,高是6cm的实心铁圆锥(完全浸没),会溢出多少毫升的水?
35.在标有比例尺的地图上,量得两地相距10厘米,一列客车和一列货车从两地同时相向而行,客车每小时行60千米,货车每小时行40千米,两车经过多少小时相遇?
36.如图所示为一个棱长6厘米的正方体,从正方体的底面向内挖去一个最大的圆锥体,剩下的体积是多少立方厘米?
37.一幢教学楼的平面图上,量的楼长16厘米,宽7.2厘米.已知比例尺是1:250,这幢教学楼的实际面积是多少平方米?
38.一列客车和一列货车同时从两个城市相对开出,客车每小时行40千米,货车的速度是客车的,两车开出2.5小时后相遇,两城相距多少千米?
39.客车和货车分别从甲乙两站同时相向开出,5小时后相遇,相遇后两车仍按原速度前进,当他们相距196千米时,客车行了全程的,货车行了全程的80%.
(1)全程是多少千米?
(2)货车行完全程需要多少个小时?
参考答案及试题解析
一.选择题
1.【考点】负数的意义及其应用.
【答案】A
【思路分析】把数据相加,得出最后的数,然后根据“上升记为正,下降记为负”计算到达楼层即可。
【解答】解:+11﹣5﹣7+15=+14
1+14=15(楼)
答:现在电梯停在15楼。
故选:A。
【名师点评】此题主要考查正负数的意义,要熟练掌握。
2.【考点】简单的等量代换问题.
【答案】B
【思路分析】根据题目中的图形就可以得到一个不等关系:□>△,一个相等关系:2个圆=1个△,就可以得到三个物体的质量的大小.
【解答】解:由第一个图可知:■>▲,
由第二个图可知:2●=▲,
所以■>▲>●,
故选:B.
【名师点评】此题主要考查了一元一次不等式组的应用,读懂图中列出不等式关系式即可求解.
3.【考点】图形的放大与缩小.
【答案】B
【思路分析】缩小后和放大后的图形与原图形相比,形状相同、大小不相同,据此解答。
【解答】解:把一个三角形按比例放大或缩小后,内角大小不变,但是边长、周长和面积都变了。
故选:B。
【名师点评】本题主要考查图形的放大与缩小的特征。
4.【考点】比的性质.
【答案】D
【思路分析】如果前项增加10,变成12,相当于前项乘6,要使比值不变,那么后项应乘6,相当于增加3的5倍,是15。
【解答】解:10+2=12
3×(12÷2﹣1)
=3×5
=15
要使比值不变,那么后项应增加15。
故选:D。
【名师点评】此题考查了比的性质,要熟练掌握。
5.【考点】设计统计活动.
【答案】C
【思路分析】根据题意安安想知道花都区2020年5月份整月的气温变化情况,因此他要做的就是把5月份每天的平均气温都要搜集出来。
【解答】解:安安想知道花都区2020年5月份整月的气温变化情况,她要搜集的数据是2020年5月每天的平均气温。
故选:C。
【名师点评】本题考查了数据整理前必需要做好数据的收集。
6.【考点】数的估算.
【答案】B
【思路分析】根据题目中的数据,据整数乘法的估算方法:把相乘的因数看成最接近它的整十、整百数来算;28≈30,365≈370,所以与28×365≈11100,11100≈1000,据此选择即可。
【解答】解:28×365≈30×370≈10000(元)
故选:B。
【名师点评】此题考查了整数乘法的估算方法,注意把相乘的数看成最接近它的整十数和几百几十的数。
7.【考点】按比例分配应用题.
【答案】C
【思路分析】根据题意可知,这一包糖为单位“1”不变,只是分的份数不同,因此求出每个人两次分得这包糖的几分之几,分率一样的即可判断分得一样多。
【解答】解:东东:3÷(3+2+5),1÷(1+2+3),两次分得不一样多,不符合题意;
青青:2÷(3+2+5),2÷(1+2+3),两次分得不一样多,不符合题意;
芳芳:5÷(3+2+5),3÷(1+2+3),两次分得一样多,符合题意。
通过以上分析可知,芳芳两次分得糖果都是,也就是这包糖果的一半,一样多。
故选:C。
【名师点评】解答此题的关键明白不管怎么分,单位“1”始终不变。
8.【考点】用角度表示方向.
【答案】C
【思路分析】依据地图上的方向辨别方法,即“上北下南、左西右东”,以及图上标注的其他信息,即可进行解答.
【解答】解:如图,以图书馆为观察点,游乐场在西偏北30°;
故选:C。
【名师点评】此题主要考查地图上的方向辨别方法的灵活应用.
9.【考点】数对与位置.
【答案】B
【思路分析】根据“第八列最后一名同学的位置是(8,6),”知道此教室里一共坐了6行同学,又知道六(3)班同学的位置设了8列,由此根据整数乘法的意义,列数即可解答.
【解答】解:8×6=48(人);
答:六(3)班共有同学48人.
故选:B。
【名师点评】此题考查了数对的意义,即数对中的第一个数表示列数;数对中的第二个数表示行数.
10.【考点】从不同方向观察物体和几何体.
【答案】A
【思路分析】分别得到3个立体图形从正面、上面、侧面所看到的图形,找到其中形状是完全一样的即可.
【解答】解:从正面、上面、侧面所看到的图形如下:
观察图形,只有从正面看所看到的立体图形的形状是完全一样的.
故选:A.
【名师点评】此题考查了从不同方向观察物体和几何体,应注意小正方形的数目及位置.
二.填空题
11.【考点】百分率应用题.
【答案】50。
【思路分析】先明确达标率,即达标学生人数占全班总人数的百分之几,把全班人数看作单位“1”,达标率为88%,则未达标的人数占总人数的1﹣88%,然后再根据百分数除法的意义进行计算即可。
【解答】解:6÷(1﹣88%)
=6÷12%
=50(人)
答:六(1)班有学生50人。
故答案为:50。
【名师点评】解答此题应先判断出单位“1”,然后根据求一个数是另一个数的百分之几,用除法计算即可.
12.【考点】有余数的除法应用题.
【答案】9。
【思路分析】根据题意,也就是求2.5升(2500毫升)里面有几个300毫升,用除法计算。
【解答】解:2.5升=2500毫升
2500÷300≈9(瓶)
答:至少需要9个这样的瓶子。
故答案为:9。
【名师点评】此题考查有余数的除法应用题,解决此题的关键是:理解“进一法”的意义,即无论结果剩多少毫升,都要再多装1瓶。
13.【考点】比的意义;百分数的意义、读写及应用.
【答案】1:4,20。
【思路分析】盐与水的比是25:100,前项后项同时除以25,化简得1:4。那么盐占盐水的1÷(1+4)×100%,计算即可。
【解答】解:25:100=1:4
1÷(1+4)×100%
=0.2×100%
=20%
答:盐与水的比是1:4,盐占盐水的20%。
故答案为:1:4,20。
【名师点评】此题主要考查了比的意义和百分数的意义,要熟练掌握。
14.【考点】确定轴对称图形的对称轴条数及位置;圆、圆环的周长;圆、圆环的面积.
【答案】见试题解答内容
【思路分析】①根据轴对称图形的定义:一个图形沿一条直线对折,直线两旁的部分能够完全重合,则这个图形就是轴对称图形,这条直线就是这个图形的一条对称轴,据此即可解答.
②根据圆的直径是C÷π,求出圆的直径,然后根据长方形的面积公式解答即可.
【解答】解:
25.12÷3.14=8(厘米)
8×2=16(厘米)
8×16=128(平方厘米)
答:如图有 2条对称轴,如果每个圆的周长是25.12cm,长方形的面积是128cm2;
故答案为:2,128
【名师点评】此题主要考查如何确定轴对称图形的对称轴条数及位置以及圆的周长和长方形面积计算方法.
15.【考点】比例尺应用题.
【答案】见试题解答内容
【思路分析】(1)已知比例尺和图上距离,要求实际距离,应根据关系式:图上距离÷比例尺=实际距离,进行解答,列式为3.
(2)已知比例尺和实际距离,要求图上距离,应根据关系式:实际距离×比例尺=图上距离,进行解答,列式为15000000.
【解答】解:(1)3,
=3×3000000,
=9000000(cm),
=90(km);
答:图上距离3cm的距离表示实际90km的距离.
(2)150km=15000000cm,
150000005(cm).
答:实际距离是150km,在这幅图上应画5cm.
故答案为:90,5.
【名师点评】此题主要考查比例尺、图上距离、实际距离三者之间的数量关系:比例尺=图上距离÷实际距离,灵活变形列式解决问题.
16.【考点】数与形结合的规律.
【答案】18。
【思路分析】观察三个图形得到一张正方形桌子可坐4人,二张正方形桌子可坐(4+2×1)人,则每增加一个桌子就可多坐两个人,于是得到n张正方形桌子可坐[4+2(n﹣1)]人。
【解答】解:由分析可得:
4+2×(8﹣1)
=4+2×7
=4+14
=18(人)
答:8张桌子排在一起,能坐18个人。
故答案为:18。
【名师点评】本题考查了图形的变化类问题,主要培养学生的观察能力和总结能力。
17.【考点】用字母表示数.
【答案】(100﹣12a);16。
【思路分析】根据题干,每天看12页,看了a天,则已经看了12a页,用总页数减去已经看完的页数,即可得到剩下的页数,再把a=7代入计算即可解答问题。
【解答】解:还剩下(100﹣12a)页
当a=7时
100﹣12×7
=100﹣84
=16(页)
答:还剩(100﹣12a)页没看,当a=7时,还剩16页没看。
故答案为:(100﹣12a);16。
【名师点评】做这类用字母表示数的题目时,解题关键是根据已知条件,把未知的数用字母正确的表示出来,然后根据题意列式计算即可得解。
18.【考点】三角形的内角和;等腰三角形与等边三角形.
【答案】见试题解答内容
【思路分析】因为等腰三角形的两个底角相等,三角形的内角和是180度,所以底角的度数=(180°﹣顶角)÷2,代入数据计算即可.
【解答】解:(180°﹣50°)÷2
=130°÷2
=65°;
答:它的其中一个底角是65°.
故答案为:65.
【名师点评】此题根据三角形内角和等于180度和等腰三角形的特点进行解答.
19.【考点】比例尺.
【答案】1:4000。
【思路分析】根据比例尺=图上距离:实际距离,代入数据解答即可。
【解答】解:3cm:120m
=3cm:12000cm
=1:4000
答:这幅地图的比例尺是1:4000。
故答案为:1:4000。
【名师点评】解答此题的关键是掌握比例尺=图上距离:实际距离这个公式。
20.【考点】小数大小的比较.
【答案】0.86,0.87,,0.8。
【思路分析】首先根据小数、分数和百分数之间的互化的方法,把其中的分数和百分数都化成小数,然后根据小数大小比较的方法,把各数按从小到大的顺序排列即可。
【解答】解:87%=0.87
0.875
0.80.8777......
0.86<0.870.8
故答案为:0.86,0.87,,0.8。
【名师点评】此题主要考查了小数、分数和百分数之间的互化的方法,以及小数大小比较的方法,要熟练掌握。
21.【考点】比的意义.
【答案】3:5。
【思路分析】把路的总米数看作单位“1”,根据小兰、小宁跑完分别需要的小时数,先分别求出小兰、小宁的速度,进而写比并化简比。
【解答】解:(1÷5):(1÷3)
:
=3:5
答:小兰和小宁速度的最简比是3:5。
故答案为:3:5。
【名师点评】本题主要考查了比的意义,用到速度=路程÷时间。
22.【考点】用字母表示数.
【答案】(a+20)÷4,30。
【思路分析】用香蕉得千克数加20千克,再除以4,即可得葡萄的千克数。把香蕉的千克数代入,计算即可。
【解答】解:(a+20)÷4
答:葡萄有(a+20)÷4千克。
(100+20)÷4
=120÷4
=30(千克)
答:如果香蕉有100千克,则葡萄有30千克。
故答案为:(a+20)÷4,30。
【名师点评】本题主要考查了用字母表示数和含字母式子求值,要分清数量关系。
三.判断题
23.【考点】正比例和反比例的意义.
【答案】见试题解答内容
【思路分析】判断小麦的总重量和面粉的重量是否成正比例,就看这两种量是否是对应的比值一定,如果是比值一定,就成正比例,如果不是比值一定或比值不一定,就不成正比例.
【解答】解:面粉的重量÷小麦的总重量×100%=小麦的出粉率(一定),是比值一定,小麦的总重量和面粉的重量成正比例.
故判断为:正确.
【名师点评】此题属于辨识成正比例的量,就看这两种量是否是对应的比值一定,再做出判断.
24.【考点】圆柱的侧面积、表面积和体积;圆锥的体积.
【答案】×
【思路分析】圆柱的体积=底面积×高,圆锥的体积底面积×高,当底面积与高相等时,圆柱的体积与圆锥的体积之比是3:1,由此即可进行判断.
【解答】解:根据圆柱与圆锥的体积公式可知:当底面积与高相等时,圆柱的体积与圆锥的体积之比是3:1,
原题中没有说“等底等高”,所以原题说法错误.
故答案为:×.
【名师点评】此题考查了等底等高的圆柱与圆锥体积的倍数关系,这里要注意数学语言的严密性.
25.【考点】分数大小的比较.
【答案】×
【思路分析】根据分数的大小比较方法,大于而小于,分母为5的真分数只有一个;但是根据分数的基本性质,把这两个分数的分子、分母同时乘、同时乘3、4、5……,这两个分数之间的分数也随之增加,所以这两个分数之间有无数个。据此判断。
【解答】解:在和之间只有一个最简真分数有无数个,所以原题说法错误。
故答案为:×。
【名师点评】两个小数之间有无数个小数,两个分数之间也有无数个分数。
26.【考点】轴对称图形的辨识.
【答案】×
【思路分析】根据轴对称图形的意义:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴;进行判断即可。
【解答】解:长方形、正方形、等腰三角形和圆都是轴对称图形,直角梯形不是轴对称图形,故原题说法错误。
故答案为:×。
【名师点评】此题考查了轴对称图形的意义,判断轴对称图形的关键是寻找对称轴,看图形对折后两部分是否完全重合。
27.【考点】用字母表示数;奇数与偶数的初步认识.
【答案】√
【思路分析】在自然数中,能被2整除的数叫作偶数,n为自然数,2n+2能被2整除,所以2n+2为偶数.
【解答】解:2n+2=2(n+1),
2(n+1)÷2=(n+1),
所以2n+2为偶数,
故答案为:√.
【名师点评】此题主要考查的是偶数的含义.
28.【考点】因数和倍数的意义.
【答案】见试题解答内容
【思路分析】一个数既是它本身的最小倍数,又是它本身的最大因数.如:5的最小倍数是5,最大因数也是5.由此即可解答.
【解答】解:因为一数既是它本身的最小倍数,又是它本身的最大因数,所以此题干不正确;
故答案为:×.
【名师点评】此题重点是考察因数和倍数的意义,要知道一数既是它本身的最小倍数,又是它本身的最大因数.
四.计算题
29.【考点】求比值和化简比;千以内加减法;数的估算;小数乘法;分数的加法和减法;分数乘法.
【答案】106;0;6000;17;0.04;0.7;;2;;25。
【思路分析】根据整数加减乘除法、小数乘除法、分数加减乘除法的计算方法计算即可;
估算时,把数看作与之接近的整十数来估算;
求比值,用比的前项除以后项即可。
【解答】解:
305﹣199=106 0 31×197≈6000 510÷30=17 0.22=0.04
3.5×0.2=0.7 2 25
【名师点评】本题考查口算,注意计算的准确性。
30.【考点】分数方程求解;解比例.
【答案】x=5;x=0.7。
【思路分析】(1)根据比例的基本性质,把原式化为x=10,然后方程的两边同时除以求解。
(2)先计算5×0.7=3.5,根据等式的性质,方程的两边同时减去3.5,然后方程的两边同时除以7求解。
【解答】解:(1)x:10:
x=10
x10
x=5
(2)7x+5×0.7=8.4
7x+3.5=8.4
7x+3.5﹣3.5=8.4﹣3.5
7x=4.9
7x÷7=4.9÷7
x=0.7
【名师点评】本题考查解方程和解比例,解题的关键是掌握等式的性质与比例的基本性质:方程两边同时加上或减去相同的数,等式仍然成立;方程两边同时乘(或除以)相同的数(0除外),等式仍然成立;两个外项的积等于两个内项的积。
31.【考点】分数的四则混合运算;分数的简便计算(运算定律的分数应用);小数乘法(推广整数乘法运算定律).
【答案】1270;21;4;20.2。
【思路分析】按照乘法分配律计算;
按照乘法分配律计算;
按照加法交换律以及减法的性质计算;
先算小括号里面的除法,再算小括号里面的加法,最后算减法。
【解答】解:12.7×99+12.7
=12.7×(99+1)
=12.7×100
=1270
=3636
=27﹣6
=21
=4()
=5﹣1
=4
=28.8﹣(7.6+1)
=28.8﹣8.6
=20.2
【名师点评】本题考查了四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
五.操作题
32.【考点】作平移后的图形;作旋转一定角度后的图形;数对与位置;作三角形的高;作轴对称图形.
【答案】见试题解答内容
【思路分析】(1)根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,即可把圆心移到(6,8)的位置上.
(2)根据旋转的特征,三角形绕点A顺时针旋转90°,点A的位置不动,其余各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形.这是一直角三角形,一条直角边是以另一条直角边为底的高,只需画出斜边上的高即可,过斜边所对角的顶点作斜边的垂直线段就是斜边上的高.
(3)根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的下边画出上图的关键对称点,依次连接即可.
【解答】解:(1)把圆移到圆心(6,8)的位置上(图中红色部分).
(2)把三角形绕A点顺时针旋转90°(图中绿色部分),再画出新三角形底边上的高(图中虚线部分).
(3)画出右上方图形的另一半,使其成为轴对称图形(图中蓝色部分).
【名师点评】此题考查的知识有:数对与位置,作旋转一定度数后的图形、作三角形的高、作轴对称图形等.
六.解答题
33.【考点】关于圆柱的应用题.
【答案】见试题解答内容
【思路分析】(1)先根据水桶的底面直径依次求出半径和底面面积,然后再根据直径和高求出水桶的侧面积,用底面面积加上侧面积即可.
(2)根据已求出的底面面积(314平方厘米)和已知高(24厘米),底面积×高=容积.
【解答】解:(1)3.143.14×20×24,
=314+1507.2,
=1821.2(平方厘米),
≈1900平方厘米.
(2)(3.14)×24,
=314×24,
=7536(毫升).
答:做这个水桶需要铁皮1900平方厘米;这个水桶能装水7536毫升.
【名师点评】此题主要考查圆柱体的体积计算公式:V=πr2h和表面积,解答时一定要注意分清题目中条件,灵活解答.
34.【考点】圆锥的体积.
【答案】157毫升。
【思路分析】由题意可知,把这个圆锥放入容器中,溢出水的体积就等于这个圆锥的体积,根据圆锥的体积公式:Vπr2h,把数据代入公式解答。
【解答】解:3.14×52×6
3.14×25×6
=157(立方厘米)
157立方厘米=157毫升
答:会溢出157毫升的水。
【名师点评】此题主要考查圆锥体积公式的灵活运用,关键是熟记公式。
35.【考点】比例尺应用题.
【答案】4小时。
【思路分析】由线段比例尺可知1厘米代表40千米,量得两地间相距10厘米,也就是10个40千米,用乘法求出两地的路程,进而根据“路程÷速度之和=相遇时间”,代入数值,解答即可。
【解答】解:10×40=400(千米)
400÷(60+40)
=400÷100
=4(小时)
答:两车经过4小时相遇。
【名师点评】此题主要考查利用线段比例尺求出实际距离的方法,再根据路程、相遇时间和速度之和三者之间的关系解答。
36.【考点】简单的立方体切拼问题;长方体和正方体的体积;圆锥的体积.
【答案】见试题解答内容
【思路分析】剩下的体积就是这个棱长为6厘米的正方体的体积与高为6厘米的圆锥的体积之差,由此只要求得圆锥的底面半径即可解决问题:圆锥的底面在正方体的底面上,根据正方形内最大圆的特点可知:圆锥的底面半径为6÷2=3厘米.
【解答】解:6×6×63.146,
=2163.14×9×6,
=216﹣56.52,
=159.48(立方厘米),
答:剩下部分的体积是159.48立方厘米.
【名师点评】此题考查了正方体与圆锥的体积公式的灵活应用,这里正确得出正方体内最大的圆锥的底面半径与高是解决此类问题的关键.
37.【考点】图上距离与实际距离的换算(比例尺的应用).
【答案】见试题解答内容
【思路分析】图上距离和比例尺已知,先依据“实际距离=图上距离÷比例尺”分别求出长和宽的实际距离,进而利用长方形的面积公式即可求解.
【解答】解:164000(厘米)=40(米)
7.21800(厘米)=18(米)
40×18=720(平方米)
答:这幢教学楼的实际面积是720平方米.
【名师点评】分别求出长和宽的实际距离,是解答本题的关键.
38.【考点】相遇问题.
【答案】见试题解答内容
【思路分析】已知客车每小时行40千米,货车的速度是客车的,根据求一个数的几分之几是多少用乘法计算,可求出货车的速度,再根据路程=速度和×时间,可求出两地之间的路程,据此解答.
【解答】解:(40+40)×2.5
=(40+32)×2.5
=72×2.5
=180(千米)
答:两城相距180千米.
【名师点评】本题的重点是先求出货车的速度,进而根据路程=速度和×时间,可求出两地之间的路程.
39.【考点】简单的行程问题;分数、百分数复合应用题.
【答案】见试题解答内容
【思路分析】(1)根据题意,客车行了全程的,货车行了全程的80%,可知两车是相遇后又分开196千米,因此全程是196÷(80%﹣1),计算即可;
(2)客车、货车的速度比为:80%=3:4,则货车速度为:(490÷5)56(千米),那么货车行完全程需要的时间是:490÷56,计算即可.
【解答】解:(1)196÷(80%﹣1),
=196÷(0.6+0.8﹣1),
=196÷0.4,
=490(千米);
答:全程是490千米.
(2)客货速度比为:
:80%=3:4;
则货车速度为:
(490÷5),
=98,
=56(千米);
货车行完全程需要的时间是:
490÷56=8(小时).
答:货车行完全程需要8小时.
【名师点评】此题在解答第二问时,关键是求出客、货两车的速度比,进而求出货车速度,根据货车的速度求得货车行完全程需要的时间.
21世纪教育网(www.21cnjy.com)
同课章节目录
