2026年中考数学一轮复习 图形认识初步(含解析)
文档属性
| 名称 | 2026年中考数学一轮复习 图形认识初步(含解析) | 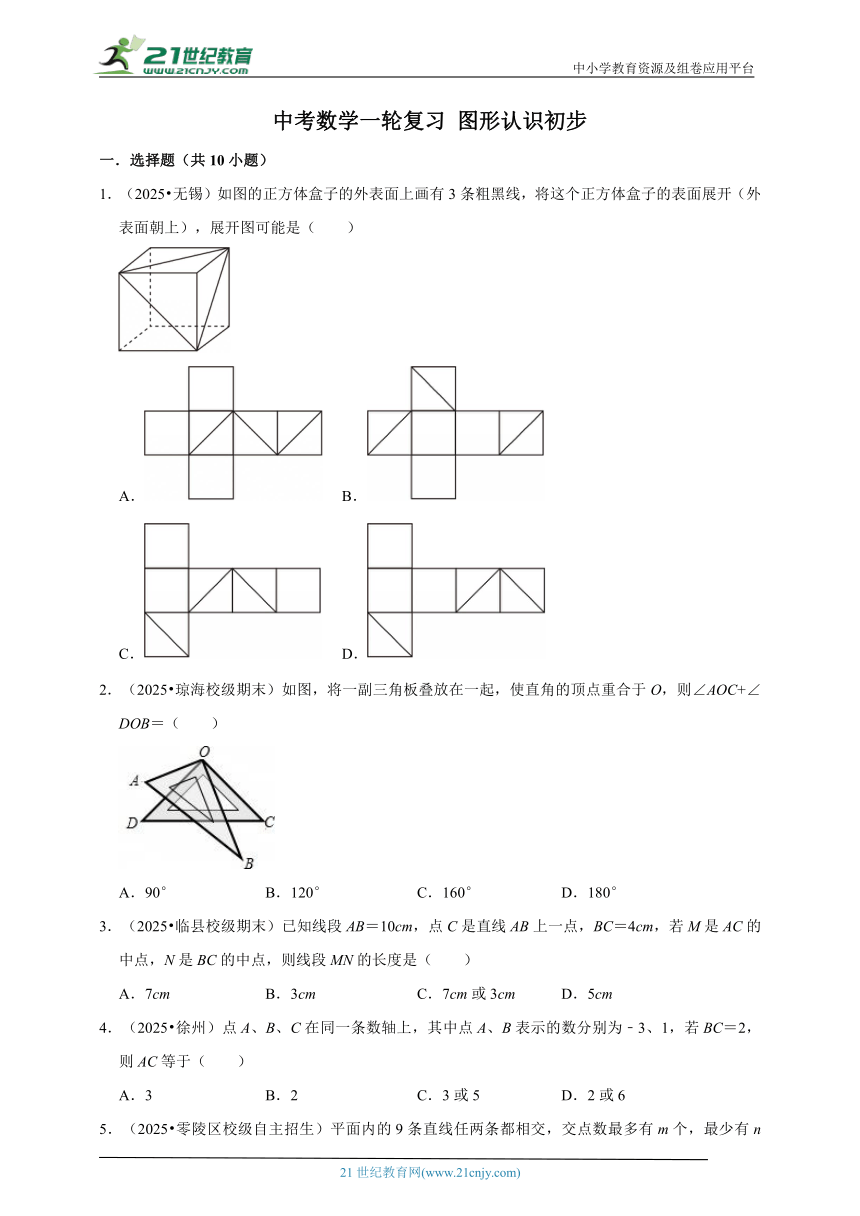 | |
| 格式 | docx | ||
| 文件大小 | 686.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 05:39:04 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中考数学一轮复习 图形认识初步
一.选择题(共10小题)
1.(2025 无锡)如图的正方体盒子的外表面上画有3条粗黑线,将这个正方体盒子的表面展开(外表面朝上),展开图可能是( )
A. B.
C. D.
2.(2025 琼海校级期末)如图,将一副三角板叠放在一起,使直角的顶点重合于O,则∠AOC+∠DOB=( )
A.90° B.120° C.160° D.180°
3.(2025 临县校级期末)已知线段AB=10cm,点C是直线AB上一点,BC=4cm,若M是AC的中点,N是BC的中点,则线段MN的长度是( )
A.7cm B.3cm C.7cm或3cm D.5cm
4.(2025 徐州)点A、B、C在同一条数轴上,其中点A、B表示的数分别为﹣3、1,若BC=2,则AC等于( )
A.3 B.2 C.3或5 D.2或6
5.(2025 零陵区校级自主招生)平面内的9条直线任两条都相交,交点数最多有m个,最少有n个,则m+n等于( )
A.36 B.37 C.38 D.39
6.(2025 霍林郭勒市期末)在下列生活、生产现象中,可以用基本事实“两点确定一条直线”来解释的是( )
①用两颗钉子就可以把木条固定在墙上;
②把笔尖看成一个点,当这个点运动时便得到一条线;
③把弯曲的公路改直,就能缩短路程;
④植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上.
A.①③ B.②④ C.①④ D.②③
7.(2025 滨州)如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,如果∠AOB=40°,∠COE=60°,则∠BOD的度数为( )
A.50° B.60° C.65° D.70°
8.(2025 金华)如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是( )
A.两点确定一条直线
B.两点之间线段最短
C.垂线段最短
D.在同一平面内,过一点有且只有一条直线与已知直线垂直
9.(2025 西宁)如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°;③(∠α+∠β);④(∠α﹣∠β).正确的有( )
A.4个 B.3个 C.2个 D.1个
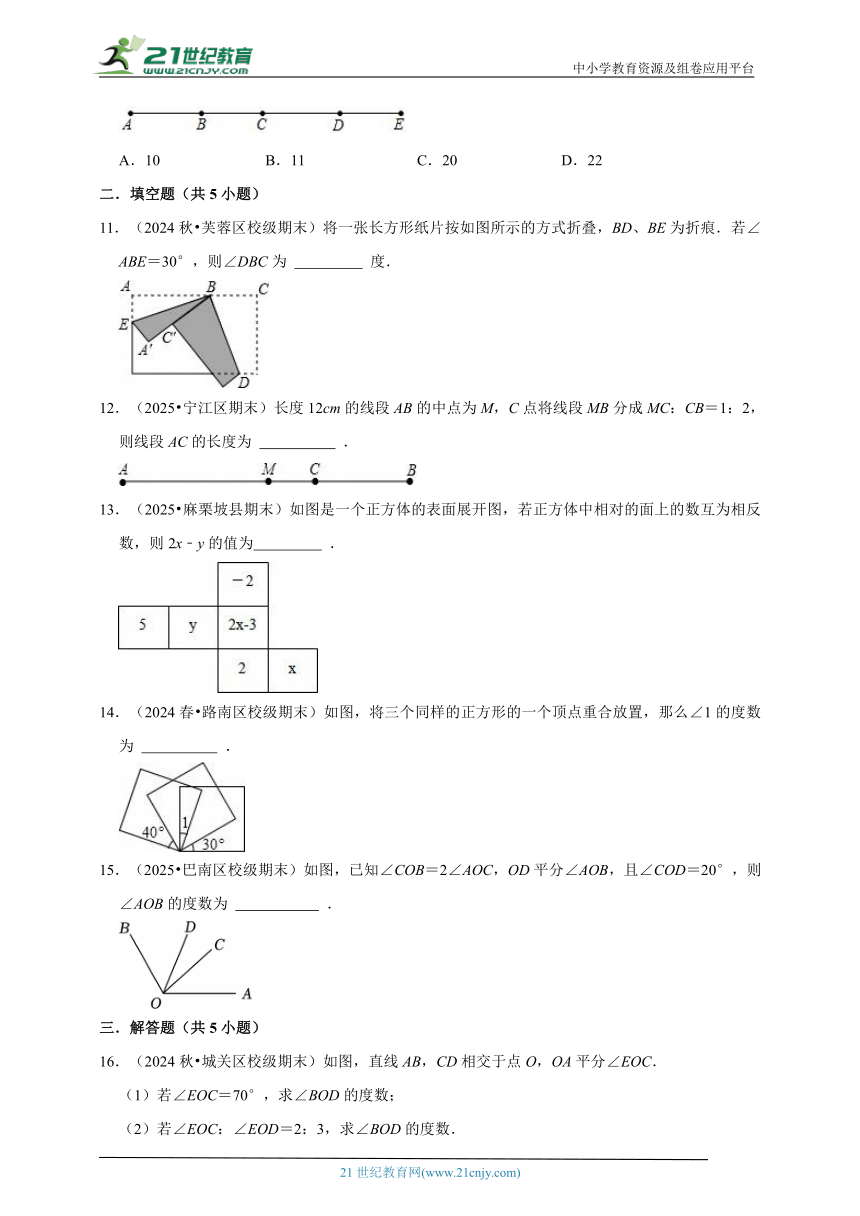
10.(2024秋 管城区校级期末)如图,AE是一段高铁行驶路线图,图中字母表示的5个点表示5个车站在这段路线上往返行车,需印制( )种车票.
A.10 B.11 C.20 D.22
二.填空题(共5小题)
11.(2024秋 芙蓉区校级期末)将一张长方形纸片按如图所示的方式折叠,BD、BE为折痕.若∠ABE=30°,则∠DBC为 度.
12.(2025 宁江区期末)长度12cm的线段AB的中点为M,C点将线段MB分成MC:CB=1:2,则线段AC的长度为 .
13.(2025 麻栗坡县期末)如图是一个正方体的表面展开图,若正方体中相对的面上的数互为相反数,则2x﹣y的值为 .
14.(2024春 路南区校级期末)如图,将三个同样的正方形的一个顶点重合放置,那么∠1的度数为 .
15.(2025 巴南区校级期末)如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=20°,则∠AOB的度数为 .
三.解答题(共5小题)
16.(2024秋 城关区校级期末)如图,直线AB,CD相交于点O,OA平分∠EOC.
(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
17.(2024 迎泽区校级开学)如图,已知线段AB和CD的公共部分BDABCD,线段AB、CD的中点E、F之间距离是10cm,求AB,CD的长.
18.(2024秋 恩施市期末)【背景知识】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点A、点B表示的数分别为a、b,则A,B两点之间的距离AB=|a﹣b|,线段AB的中点表示的数为.
【问题情境】如图,数轴上点A表示的数为﹣2,点B表示的数为8,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
【综合运用】
(1)填空:
①A、B两点间的距离AB= ,线段AB的中点表示的数为 ;
②用含t的代数式表示:t秒后,点P表示的数为 ;点Q表示的数为 .
(2)求当t为何值时,P、Q两点相遇,并写出相遇点所表示的数;
(3)求当t为何值时,PQAB;
(4)若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.
19.(2025 五华县期末)如图,OM是∠AOC的平分线,ON是∠BOC的平分线.
(1)如图1,当∠AOB是直角,∠BOC=60°时,∠MON的度数是多少?
(2)如图2,当∠AOB=α,∠BOC=60°时,猜想∠MON与α的数量关系;
(3)如图3,当∠AOB=α,∠BOC=β时,猜想∠MON与α、β有数量关系吗?如果有,指出结论并说明理由.
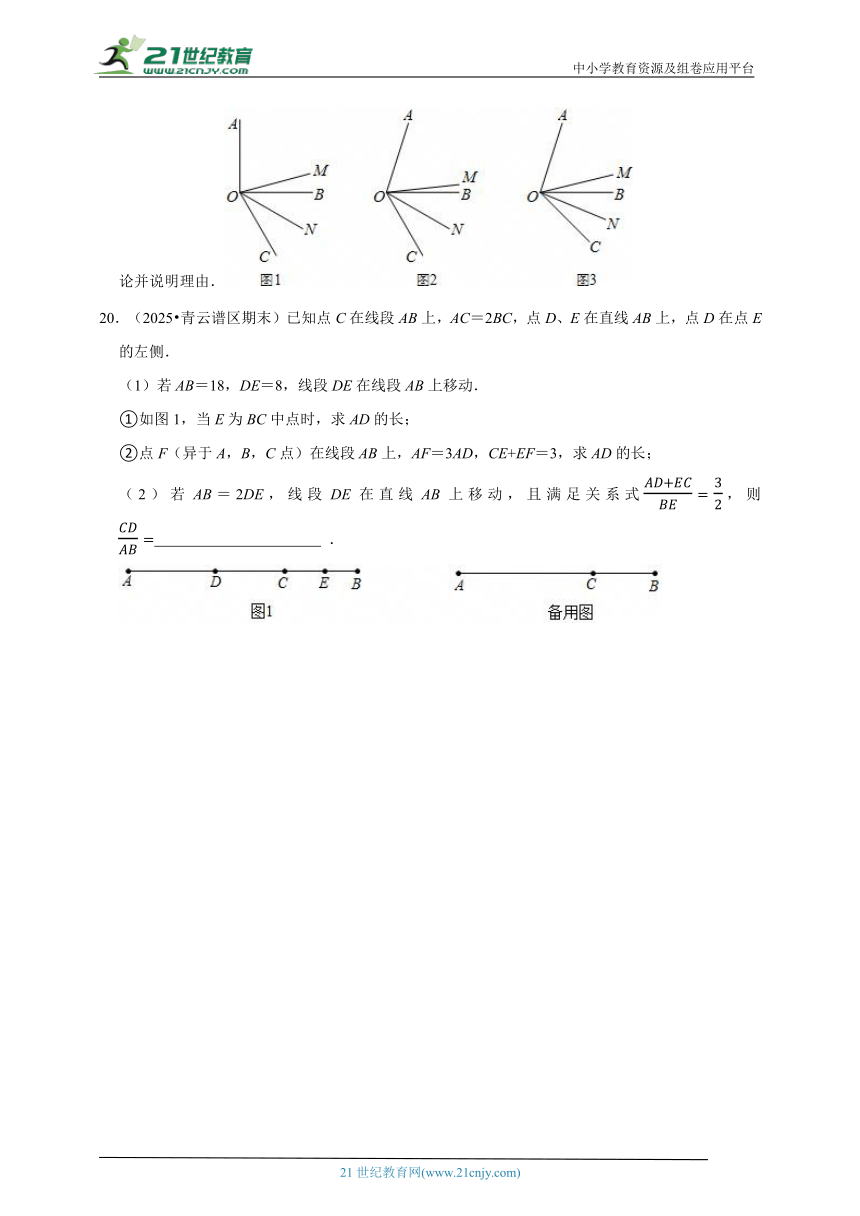
20.(2025 青云谱区期末)已知点C在线段AB上,AC=2BC,点D、E在直线AB上,点D在点E的左侧.
(1)若AB=18,DE=8,线段DE在线段AB上移动.
①如图1,当E为BC中点时,求AD的长;
②点F(异于A,B,C点)在线段AB上,AF=3AD,CE+EF=3,求AD的长;
(2)若AB=2DE,线段DE在直线AB上移动,且满足关系式,则 .
中考数学一轮复习 图形认识初步
一.选择题(共10小题)
1.(2025 无锡)如图的正方体盒子的外表面上画有3条粗黑线,将这个正方体盒子的表面展开(外表面朝上),展开图可能是( )
A. B.
C. D.
【考点】几何体的展开图.
【答案】D
【分析】根据正方体的表面展开图进行分析解答即可.
【解答】解:根据正方体的表面展开图,两条黑线在一列,故A错误,且两条相邻成直角,故B错误,正视图的斜线方向相反,故C错误,只有D选项符合条件,
故选:D.
【点评】本题主要考查了几何体的展开图,注意正方体的空间图形,从相对面入手,分析及解答问题.
2.(2025 琼海校级期末)如图,将一副三角板叠放在一起,使直角的顶点重合于O,则∠AOC+∠DOB=( )
A.90° B.120° C.160° D.180°
【考点】角的计算.
【答案】D
【分析】因为本题中∠AOC始终在变化,因此可以采用“设而不求”的解题技巧进行求解.
【解答】解:设∠AOD=a,∠AOC=90°+a,∠BOD=90°﹣a,
所以∠AOC+∠BOD=90°+a+90°﹣a=180°.
故选:D.
【点评】本题考查了角度的计算问题,在本题中要注意∠AOC始终在变化,因此可以采用“设而不求”的解题技巧进行求解.
3.(2025 临县校级期末)已知线段AB=10cm,点C是直线AB上一点,BC=4cm,若M是AC的中点,N是BC的中点,则线段MN的长度是( )
A.7cm B.3cm C.7cm或3cm D.5cm
【考点】比较线段的长短.
【专题】分类讨论;推理能力.
【答案】D
【分析】本题应考虑到A、B、C三点之间的位置关系的多种可能,即当点C在线段AB上时和当点C在线段AB的延长线上时.
【解答】解:(1)当点C在线段AB上时,则MNACBCAB=5cm;
(2)当点C在线段AB的延长线上时,则MNACBC=7﹣2=5cm.
综合上述情况,线段MN的长度是5cm.
故选:D.
【点评】首先要根据题意,考虑所有可能情况,画出正确图形.再根据中点的概念,进行线段的计算.
4.(2025 徐州)点A、B、C在同一条数轴上,其中点A、B表示的数分别为﹣3、1,若BC=2,则AC等于( )
A.3 B.2 C.3或5 D.2或6
【考点】两点间的距离;数轴.
【专题】压轴题.
【答案】D
【分析】要求学生分情况讨论A,B,C三点的位置关系,即点C在线段AB内,点C在线段AB外.
【解答】解:此题画图时会出现两种情况,即点C在线段AB内,点C在线段AB外,所以要分两种情况计算.
点A、B表示的数分别为﹣3、1,
AB=4.
第一种情况:在线段AB外,
AC=4+2=6;
第二种情况:在线段AB内,
AC=4﹣2=2.
故选:D.
【点评】在未画图类问题中,正确画图很重要.本题渗透了分类讨论的思想,体现了思维的严密性,在今后解决类似的问题时,要防止漏解.
5.(2025 零陵区校级自主招生)平面内的9条直线任两条都相交,交点数最多有m个,最少有n个,则m+n等于( )
A.36 B.37 C.38 D.39
【考点】直线、射线、线段.
【专题】压轴题;规律型.
【答案】B
【分析】求出平面内的9条直线任两条都相交,交点数最多的个数,再求得最少的个数;则即可求得m+n的值.
【解答】解:三条最多交点数的情况.就是第三条与前面两条都相交:1+2
四条最多交点数的情况.就是第四条与前面三条都相交:1+2+3
五条最多交点数的情况.就是第五条与前面四条都相交:1+2+3+4
六条最多交点数的情况.就是第六条与前面五条都相交:1+2+3+4+5
七条最多交点数的情况.就是第七条与前面六条都相交:1+2+3+4+5+6
八条最多交点数的情况.就是第八条与前面七条都相交:1+2+3+4+5+6+7
九条最多交点数的情况.就是第九条与前面八条都相交:1+2+3+4+5+6+7+8=36
当平面内的9条直线相交于同一点时,交点数最少,即n=1
则m+n=1+36=37
故选:B.
【点评】此题考查了平面图形,主要培养学生的观察能力和几何想象能力.
6.(2025 霍林郭勒市期末)在下列生活、生产现象中,可以用基本事实“两点确定一条直线”来解释的是( )
①用两颗钉子就可以把木条固定在墙上;
②把笔尖看成一个点,当这个点运动时便得到一条线;
③把弯曲的公路改直,就能缩短路程;
④植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上.
A.①③ B.②④ C.①④ D.②③
【考点】直线的性质:两点确定一条直线.
【专题】平移、旋转与对称;推理能力.
【答案】C
【分析】直接利用直线的性质以及线段的性质分析得出答案.
【解答】解:①用两颗钉子就可以把木条固定在墙上,可以用基本事实“两点确定一条直线”来解释;
②把笔尖看成一个点,当这个点运动时便得到一条线,可以用基本事实“无数个点组成线”来解释;
③把弯曲的公路改直,就能缩短路程,可以用基本事实“两点之间线段最短”来解释;
④植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上,可以用基本事实“两点确定一条直线”来解释.
故选:C.
【点评】此题主要考查了直线的性质以及线段的性质,正确把握相关性质是解题关键.
7.(2025 滨州)如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,如果∠AOB=40°,∠COE=60°,则∠BOD的度数为( )
A.50° B.60° C.65° D.70°
【考点】角的计算;角平分线的定义.
【专题】计算题.
【答案】D
【分析】先根据OB是∠AOC的角平分线,OD是∠COE的角平分线,∠AOB=40°,∠COE=60°求出∠BOC与∠COD的度数,再根据∠BOD=∠BOC+∠COD即可得出结论.
【解答】解:∵OB是∠AOC的角平分线,OD是∠COE的角平分线,∠AOB=40°,∠COE=60°,
∴∠BOC=∠AOB=40°,∠COD∠COE60°=30°,
∴∠BOD=∠BOC+∠COD=40°+30°=70°.
故选:D.
【点评】本题考查的是角的计算,熟知角平分线的定义是解答此题的关键.
8.(2025 金华)如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是( )
A.两点确定一条直线
B.两点之间线段最短
C.垂线段最短
D.在同一平面内,过一点有且只有一条直线与已知直线垂直
【考点】直线的性质:两点确定一条直线.
【专题】应用题.
【答案】A
【分析】根据公理“两点确定一条直线”来解答即可.
【解答】解:经过刨平的木板上的两个点,能弹出一条笔直的墨线,此操作的依据是两点确定一条直线.
故选:A.
【点评】此题考查的是直线的性质在实际生活中的运用,此类题目有利于培养学生生活联系实际的能力.
9.(2025 西宁)如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°;③(∠α+∠β);④(∠α﹣∠β).正确的有( )
A.4个 B.3个 C.2个 D.1个
【考点】余角和补角.
【专题】压轴题.
【答案】B
【分析】根据角的性质,互补两角之和为180°,互余两角之和为90°,可将,①②③④中的式子化为含有∠α+∠β的式子,再将∠α+∠β=180°代入即可解出此题.
【解答】解:∵∠α和∠β互补,
∴∠α+∠β=180°.因为90°﹣∠β+∠β=90°,所以①正确;
又∠α﹣90°+∠β=∠α+∠β﹣90°=180°﹣90°=90°,②也正确;
(∠α+∠β)+∠β180°+∠β=90°+∠β≠90°,所以③错误;
(∠α﹣∠β)+∠β(∠α+∠β)180°=90°,所以④正确.
综上可知,①②④均正确.
故选:B.
【点评】本题考查了角之间互补与互余的关系,互补两角之和为180°,互余两角之和为90°.
10.(2024秋 管城区校级期末)如图,AE是一段高铁行驶路线图,图中字母表示的5个点表示5个车站在这段路线上往返行车,需印制( )种车票.
A.10 B.11 C.20 D.22
【考点】直线、射线、线段.
【专题】推理填空题;模型思想.
【答案】C
【分析】观察可以发现,每个车站作为起始站,可以到达除本站外的任何一个站,需要印制(5﹣1)种车票,而有5个起始站,故可以直接列出算式.
【解答】解:图中线段有AB,AC,AD,AE,BC,BD,BE,CD,CE,DE,共10条,单程要10种车票,往返就是20种,即5×(5﹣1)=20,
故选:C.
【点评】本题在线段的基础上,考查了排列与组合的知识,解题关键是要理解题意,每个车站都既可以作为起始站,可以到达除本站外的任何一个站.
二.填空题(共5小题)
11.(2024秋 芙蓉区校级期末)将一张长方形纸片按如图所示的方式折叠,BD、BE为折痕.若∠ABE=30°,则∠DBC为 60 度.
【考点】角的计算.
【专题】推理填空题;线段、角、相交线与平行线;推理能力.
【答案】见试题解答内容
【分析】根据折叠思想,通过角的和差计算即可求解.
【解答】解:∵BD、BE为折痕,∴BD、BE分别平分∠CBC′、∠ABA′
∴∠A′BE=∠ABE=30°,
∠DBC=∠DBC′
∵∠A′BE+∠ABE+∠DBC+∠DBC′=180°
∴∠ABE+∠DBC=90°
∴∠DBC=60°.
故答案为:60.
【点评】本题考查了角的计算,用正确角分线是解决本题的关键.
12.(2025 宁江区期末)长度12cm的线段AB的中点为M,C点将线段MB分成MC:CB=1:2,则线段AC的长度为 8cm .
【考点】比较线段的长短.
【专题】计算题.
【答案】见试题解答内容
【分析】先由中点的定义求出AM,BM的长,再根据MC:CB=1:2的关系,求MC的长,最后利用AC=AM+MC得其长度.
【解答】解:∵线段AB的中点为M,
∴AM=BM=6cm
设MC=x,则CB=2x,
∴x+2x=6,解得x=2
即MC=2cm.
∴AC=AM+MC=6+2=8cm.
【点评】利用中点性质转化线段之间的倍分关系是解题的关键,同时灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点.
13.(2025 麻栗坡县期末)如图是一个正方体的表面展开图,若正方体中相对的面上的数互为相反数,则2x﹣y的值为 ﹣3 .
【考点】专题:正方体相对两个面上的文字.
【专题】图表型.
【答案】见试题解答内容
【分析】根据正方体的展开图中相对面不存在公共点可找出5对面的数字,从而可根据相反数的定义求得x的值,进一步求得y的值,最后代入计算即可.
【解答】解:∵“5”与“2x﹣3”是对面,“x”与“y”是对面,
∴2x﹣3=﹣5,y=﹣x,
解得x=﹣1,y=1,
∴2x﹣y=﹣2﹣1=﹣3.
故答案为:﹣3.
【点评】本题主要考查的是正方体相对面上的文字,掌握正方体的展开图中相对面不存在公共点是解题的关键.
14.(2024春 路南区校级期末)如图,将三个同样的正方形的一个顶点重合放置,那么∠1的度数为 20° .
【考点】角的计算.
【专题】计算题.
【答案】见试题解答内容
【分析】根据∠1=∠BOD+EOC﹣∠BOE,利用正方形的角都是直角,即可求得∠BOD和∠EOC的度数从而求解.
【解答】解:∵∠BOD=90°﹣∠AOB=90°﹣30°=60°
∠EOC=90°﹣∠EOF=90°﹣40°=50°
又∵∠1=∠BOD+∠EOC﹣∠BOE
∴∠1=60°+50°﹣90°=20°
故答案为:20°.
【点评】本题主要考查了角度的计算,正确理解∠1=∠BOD+EOC﹣∠BOE这一关系是解决本题的关键.
15.(2025 巴南区校级期末)如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=20°,则∠AOB的度数为 120° .
【考点】角的计算;角平分线的定义.
【答案】见试题解答内容
【分析】根据角平分线的性质得出∠COB=2∠AOC=2x,∠AOD=∠BOD=1.5x,进而求出x的值,即可得出答案.
【解答】解:∵∠COB=2∠AOC,OD平分∠AOB,且∠COD=20°,
∴设∠COB=2∠AOC=2x,∠AOD=∠BOD=1.5x,
∴∠COD=0.5x=20°,
∴x=40°,
∴∠AOB的度数为:3×40°=120°.
故答案为:120°.
【点评】此题主要考查了角平分线的性质,根据题意得出∠COD=0.5x是解题关键.
三.解答题(共5小题)
16.(2024秋 城关区校级期末)如图,直线AB,CD相交于点O,OA平分∠EOC.
(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
【考点】角的计算.
【专题】计算题.
【答案】见试题解答内容
【分析】(1)根据角平分线定义得到∠AOC∠EOC70°=35°,然后根据对顶角相等得到∠BOD=∠AOC=35°;
(2)先设∠EOC=2x,∠EOD=3x,根据平角的定义得2x+3x=180°,解得x=36°,则∠EOC=2x=72°,然后与(1)的计算方法一样.
【解答】解:(1)∵OA平分∠EOC,
∴∠AOC∠EOC70°=35°,
∴∠BOD=∠AOC=35°;
(2)设∠EOC=2x,∠EOD=3x,根据题意得2x+3x=180°,解得x=36°,
∴∠EOC=2x=72°,
∴∠AOC∠EOC72°=36°,
∴∠BOD=∠AOC=36°.
【点评】考查了角的计算:1直角=90°;1平角=180°.也考查了角平分线的定义和对顶角的性质.
17.(2024 迎泽区校级开学)如图,已知线段AB和CD的公共部分BDABCD,线段AB、CD的中点E、F之间距离是10cm,求AB,CD的长.
【考点】两点间的距离.
【专题】方程思想.
【答案】见试题解答内容
【分析】先设BD=xcm,由题意得AB=3xcm,CD=4xcm,AC=6xcm,再根据中点的定义,用含x的式子表示出AE和CF,再根据EF=AC﹣AE﹣CF=2.5x,且E、F之间距离是10cm,所以2.5x=10,解方程求得x的值,即可求AB,CD的长.
【解答】解:设BD=xcm,则AB=3xcm,CD=4xcm,AC=6xcm.
∵点E、点F分别为AB、CD的中点,∴AEAB=1.5xcm,CFCD=2xcm.
∴EF=AC﹣AE﹣CF=6x﹣1.5x﹣2x=2.5xcm.∵EF=10cm,∴2.5x=10,解得:x=4.
∴AB=12cm,CD=16cm.
【点评】本题主要考查了两点间的距离和中点的定义,注意运用数形结合思想和方程思想.
18.(2024秋 恩施市期末)【背景知识】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点A、点B表示的数分别为a、b,则A,B两点之间的距离AB=|a﹣b|,线段AB的中点表示的数为.
【问题情境】如图,数轴上点A表示的数为﹣2,点B表示的数为8,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
【综合运用】
(1)填空:
①A、B两点间的距离AB= 10 ,线段AB的中点表示的数为 3 ;
②用含t的代数式表示:t秒后,点P表示的数为 ﹣2+3t ;点Q表示的数为 8﹣2t .
(2)求当t为何值时,P、Q两点相遇,并写出相遇点所表示的数;
(3)求当t为何值时,PQAB;
(4)若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.
【考点】两点间的距离;数轴;绝对值;一元一次方程的应用.
【答案】见试题解答内容
【分析】(1)根据题意即可得到结论;
(2)当P、Q两点相遇时,P、Q表示的数相等列方程得到t=2,于是得到当t=2时,P、Q相遇,即可得到结论;
(3)由t秒后,点P表示的数﹣2+3t,点Q表示的数为8﹣2t,于是得到PQ=|(﹣2+3t)﹣(8﹣2t)|=|5t﹣10|,列方程即可得到结论;
(4)由点M表示的数为 2,点N表示的数为 3,即可得到结论.
【解答】解:(1)①10,3;
②﹣2+3t,8﹣2t;
(2)∵当P、Q两点相遇时,P、Q表示的数相等
∴﹣2+3t=8﹣2t,
解得:t=2,
∴当t=2时,P、Q相遇,
此时,﹣2+3t=﹣2+3×2=4,
∴相遇点表示的数为4;
(3)∵t秒后,点P表示的数﹣2+3t,点Q表示的数为8﹣2t,
∴PQ=|(﹣2+3t)﹣(8﹣2t)|=|5t﹣10|,
又PQAB10=5,
∴|5t﹣10|=5,
解得:t=1或3,
∴当:t=1或3时,PQAB;
(4)不变.
∵点M表示的数为 2,
点N表示的数为 3,
∴MN=|(2)﹣(3)|=|23|=5.
【点评】本题考查了一元一次方程的应用和数轴,解题的关键是掌握点的移动与点所表示的数之间的关系,根据题目给出的条件,找出合适的等量关系列出方程,再求解.
19.(2025 五华县期末)如图,OM是∠AOC的平分线,ON是∠BOC的平分线.
(1)如图1,当∠AOB是直角,∠BOC=60°时,∠MON的度数是多少?
(2)如图2,当∠AOB=α,∠BOC=60°时,猜想∠MON与α的数量关系;
(3)如图3,当∠AOB=α,∠BOC=β时,猜想∠MON与α、β有数量关系吗?如果有,指出结论并说明理由.
【考点】角的计算;角平分线的定义.
【答案】见试题解答内容
【分析】(1)求出∠AOC度数,求出∠MOC和∠NOC的度数,代入∠MON=∠MOC﹣∠NOC求出即可;
(2)求出∠AOC度数,求出∠MOC和∠NOC的度数,代入∠MON=∠MOC﹣∠NOC求出即可;
(3)求出∠AOC度数,求出∠MOC和∠NOC的度数,代入∠MON=∠MOC﹣∠NOC求出即可.
【解答】解:(1)如图1,∵∠AOB=90°,∠BOC=60°,
∴∠AOC=90°+60°=150°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC∠AOC=75°,∠NOC∠BOC=30°
∴∠MON=∠MOC﹣∠NOC=45°.
(2)如图2,∠MONα,
理由是:∵∠AOB=α,∠BOC=60°,
∴∠AOC=α+60°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC∠AOCα+30°,∠NOC∠BOC=30°
∴∠MON=∠MOC﹣∠NOC=(α+30°)﹣30°α.
(3)如图3,∠MONα,与β的大小无关.
理由:∵∠AOB=α,∠BOC=β,
∴∠AOC=α+β.
∵OM是∠AOC的平分线,ON是∠BOC的平分线,
∴∠MOC∠AOC(α+β),
∠NOC∠BOCβ,
∴∠MON=∠MOC﹣∠NOC
(α+β)β
α
即∠MONα.
【点评】本题考查了角平分线定义和角的有关计算,关键是求出∠AOC、∠MOC、∠NOC的度数和得出∠MON=∠MOC﹣∠NOC.
20.(2025 青云谱区期末)已知点C在线段AB上,AC=2BC,点D、E在直线AB上,点D在点E的左侧.
(1)若AB=18,DE=8,线段DE在线段AB上移动.
①如图1,当E为BC中点时,求AD的长;
②点F(异于A,B,C点)在线段AB上,AF=3AD,CE+EF=3,求AD的长;
(2)若AB=2DE,线段DE在直线AB上移动,且满足关系式,则 或 .
【考点】两点间的距离.
【专题】压轴题;线段、角、相交线与平行线;运算能力;推理能力.
【答案】见试题解答内容
【分析】(1)根据AC=2BC,AB=18,DE=8,线段DE在线段AB上移动.
①如图1,当E为BC中点时,根据中点定义即可求AD的长;
②点F(异于A,B,C点)在线段AB上,AF=3AD,CE+EF=3,确定点F是BC的中点,即可求AD的长;
(2)根据AC=2BC,AB=2DE,线段DE在直线AB上移动,满足关系式,可以设CE=x,DC=y,用含x和y的式子表示线段长,从而得出x与y的等量关系,即可求出的值.
【解答】解:(1)AC=2BC,AB=18,DE=8,
∴BC=6,AC=12,
①如图,
∵E为BC中点,
∴CE=3,
∴CD=5,
∴AD=AB﹣DB=18﹣11=7;
②如图,
Ⅰ、当点E在点F的左侧,
∵CE+EF=3,BC=6,
∴点F是BC的中点,
∴CF=BF=3,
∴AF=AB﹣BF=18﹣3=15,
∴ADAF=5;
Ⅱ、当点E在点F的右侧,
∵AC=12,CE+EF=CF=3,
∴AF=AC﹣CF=9,
∴AF=3AD=9,
∴AD=3.
其他情况不存在,舍去.
综上所述:AD的长为3或5;
(2)∵AC=2BC,AB=2DE,满足关系式,
Ⅰ、当点E在点C右侧时,如图,
设CE=x,DC=y,
则DE=x+y,
∴AB=2(x+y)
ACAB(x+y)
∴AD=AC﹣DCxy
BCAB(x+y)
∴BE=BC﹣CEyx
∴AD+ECxy
∵2(AD+EC)=3BE
∴2(xy)=3(yx)
解得,17x=4y,
∴.
Ⅱ、当点E在点A左侧时,如图,
设CE=x,DC=y,
则DE=y﹣x,
∴AB=2(y﹣x)
ACAB(y﹣x)
∴AD=DC﹣ACxy
BCAB(y﹣x)
∴BE=BC+CEyx
∴AD+ECxy
∵2(AD+EC)=3BE
∴2(xy)=3(yx)
解得,11x=8y,
∴.
点D在C点右侧,及点D在B点右侧,
无解,不符合题意;
当DE在线段AC内部时,如图,
设CE=x,DC=y,
则DE=y﹣x,
∴AB=2(y﹣x),
ACAB(y﹣x),
∴AD=AC﹣DCyx,
BCAB(y﹣x),
∴BE=BC+CEyx,
∴AD+ECxy,
∵2(AD+EC)=3BE
∴2(xy)=3(yx),
解得,﹣5x=4y(不符合题意,舍去),
∴,不符合题意,舍去.
其他情况不存在,舍去.
故答案为或.
【点评】本题考查了两点间的距离,比较难,需要仔细思考和解答.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考数学一轮复习 图形认识初步
一.选择题(共10小题)
1.(2025 无锡)如图的正方体盒子的外表面上画有3条粗黑线,将这个正方体盒子的表面展开(外表面朝上),展开图可能是( )
A. B.
C. D.
2.(2025 琼海校级期末)如图,将一副三角板叠放在一起,使直角的顶点重合于O,则∠AOC+∠DOB=( )
A.90° B.120° C.160° D.180°
3.(2025 临县校级期末)已知线段AB=10cm,点C是直线AB上一点,BC=4cm,若M是AC的中点,N是BC的中点,则线段MN的长度是( )
A.7cm B.3cm C.7cm或3cm D.5cm
4.(2025 徐州)点A、B、C在同一条数轴上,其中点A、B表示的数分别为﹣3、1,若BC=2,则AC等于( )
A.3 B.2 C.3或5 D.2或6
5.(2025 零陵区校级自主招生)平面内的9条直线任两条都相交,交点数最多有m个,最少有n个,则m+n等于( )
A.36 B.37 C.38 D.39
6.(2025 霍林郭勒市期末)在下列生活、生产现象中,可以用基本事实“两点确定一条直线”来解释的是( )
①用两颗钉子就可以把木条固定在墙上;
②把笔尖看成一个点,当这个点运动时便得到一条线;
③把弯曲的公路改直,就能缩短路程;
④植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上.
A.①③ B.②④ C.①④ D.②③
7.(2025 滨州)如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,如果∠AOB=40°,∠COE=60°,则∠BOD的度数为( )
A.50° B.60° C.65° D.70°
8.(2025 金华)如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是( )
A.两点确定一条直线
B.两点之间线段最短
C.垂线段最短
D.在同一平面内,过一点有且只有一条直线与已知直线垂直
9.(2025 西宁)如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°;③(∠α+∠β);④(∠α﹣∠β).正确的有( )
A.4个 B.3个 C.2个 D.1个
10.(2024秋 管城区校级期末)如图,AE是一段高铁行驶路线图,图中字母表示的5个点表示5个车站在这段路线上往返行车,需印制( )种车票.
A.10 B.11 C.20 D.22
二.填空题(共5小题)
11.(2024秋 芙蓉区校级期末)将一张长方形纸片按如图所示的方式折叠,BD、BE为折痕.若∠ABE=30°,则∠DBC为 度.
12.(2025 宁江区期末)长度12cm的线段AB的中点为M,C点将线段MB分成MC:CB=1:2,则线段AC的长度为 .
13.(2025 麻栗坡县期末)如图是一个正方体的表面展开图,若正方体中相对的面上的数互为相反数,则2x﹣y的值为 .
14.(2024春 路南区校级期末)如图,将三个同样的正方形的一个顶点重合放置,那么∠1的度数为 .
15.(2025 巴南区校级期末)如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=20°,则∠AOB的度数为 .
三.解答题(共5小题)
16.(2024秋 城关区校级期末)如图,直线AB,CD相交于点O,OA平分∠EOC.
(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
17.(2024 迎泽区校级开学)如图,已知线段AB和CD的公共部分BDABCD,线段AB、CD的中点E、F之间距离是10cm,求AB,CD的长.
18.(2024秋 恩施市期末)【背景知识】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点A、点B表示的数分别为a、b,则A,B两点之间的距离AB=|a﹣b|,线段AB的中点表示的数为.
【问题情境】如图,数轴上点A表示的数为﹣2,点B表示的数为8,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
【综合运用】
(1)填空:
①A、B两点间的距离AB= ,线段AB的中点表示的数为 ;
②用含t的代数式表示:t秒后,点P表示的数为 ;点Q表示的数为 .
(2)求当t为何值时,P、Q两点相遇,并写出相遇点所表示的数;
(3)求当t为何值时,PQAB;
(4)若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.
19.(2025 五华县期末)如图,OM是∠AOC的平分线,ON是∠BOC的平分线.
(1)如图1,当∠AOB是直角,∠BOC=60°时,∠MON的度数是多少?
(2)如图2,当∠AOB=α,∠BOC=60°时,猜想∠MON与α的数量关系;
(3)如图3,当∠AOB=α,∠BOC=β时,猜想∠MON与α、β有数量关系吗?如果有,指出结论并说明理由.
20.(2025 青云谱区期末)已知点C在线段AB上,AC=2BC,点D、E在直线AB上,点D在点E的左侧.
(1)若AB=18,DE=8,线段DE在线段AB上移动.
①如图1,当E为BC中点时,求AD的长;
②点F(异于A,B,C点)在线段AB上,AF=3AD,CE+EF=3,求AD的长;
(2)若AB=2DE,线段DE在直线AB上移动,且满足关系式,则 .
中考数学一轮复习 图形认识初步
一.选择题(共10小题)
1.(2025 无锡)如图的正方体盒子的外表面上画有3条粗黑线,将这个正方体盒子的表面展开(外表面朝上),展开图可能是( )
A. B.
C. D.
【考点】几何体的展开图.
【答案】D
【分析】根据正方体的表面展开图进行分析解答即可.
【解答】解:根据正方体的表面展开图,两条黑线在一列,故A错误,且两条相邻成直角,故B错误,正视图的斜线方向相反,故C错误,只有D选项符合条件,
故选:D.
【点评】本题主要考查了几何体的展开图,注意正方体的空间图形,从相对面入手,分析及解答问题.
2.(2025 琼海校级期末)如图,将一副三角板叠放在一起,使直角的顶点重合于O,则∠AOC+∠DOB=( )
A.90° B.120° C.160° D.180°
【考点】角的计算.
【答案】D
【分析】因为本题中∠AOC始终在变化,因此可以采用“设而不求”的解题技巧进行求解.
【解答】解:设∠AOD=a,∠AOC=90°+a,∠BOD=90°﹣a,
所以∠AOC+∠BOD=90°+a+90°﹣a=180°.
故选:D.
【点评】本题考查了角度的计算问题,在本题中要注意∠AOC始终在变化,因此可以采用“设而不求”的解题技巧进行求解.
3.(2025 临县校级期末)已知线段AB=10cm,点C是直线AB上一点,BC=4cm,若M是AC的中点,N是BC的中点,则线段MN的长度是( )
A.7cm B.3cm C.7cm或3cm D.5cm
【考点】比较线段的长短.
【专题】分类讨论;推理能力.
【答案】D
【分析】本题应考虑到A、B、C三点之间的位置关系的多种可能,即当点C在线段AB上时和当点C在线段AB的延长线上时.
【解答】解:(1)当点C在线段AB上时,则MNACBCAB=5cm;
(2)当点C在线段AB的延长线上时,则MNACBC=7﹣2=5cm.
综合上述情况,线段MN的长度是5cm.
故选:D.
【点评】首先要根据题意,考虑所有可能情况,画出正确图形.再根据中点的概念,进行线段的计算.
4.(2025 徐州)点A、B、C在同一条数轴上,其中点A、B表示的数分别为﹣3、1,若BC=2,则AC等于( )
A.3 B.2 C.3或5 D.2或6
【考点】两点间的距离;数轴.
【专题】压轴题.
【答案】D
【分析】要求学生分情况讨论A,B,C三点的位置关系,即点C在线段AB内,点C在线段AB外.
【解答】解:此题画图时会出现两种情况,即点C在线段AB内,点C在线段AB外,所以要分两种情况计算.
点A、B表示的数分别为﹣3、1,
AB=4.
第一种情况:在线段AB外,
AC=4+2=6;
第二种情况:在线段AB内,
AC=4﹣2=2.
故选:D.
【点评】在未画图类问题中,正确画图很重要.本题渗透了分类讨论的思想,体现了思维的严密性,在今后解决类似的问题时,要防止漏解.
5.(2025 零陵区校级自主招生)平面内的9条直线任两条都相交,交点数最多有m个,最少有n个,则m+n等于( )
A.36 B.37 C.38 D.39
【考点】直线、射线、线段.
【专题】压轴题;规律型.
【答案】B
【分析】求出平面内的9条直线任两条都相交,交点数最多的个数,再求得最少的个数;则即可求得m+n的值.
【解答】解:三条最多交点数的情况.就是第三条与前面两条都相交:1+2
四条最多交点数的情况.就是第四条与前面三条都相交:1+2+3
五条最多交点数的情况.就是第五条与前面四条都相交:1+2+3+4
六条最多交点数的情况.就是第六条与前面五条都相交:1+2+3+4+5
七条最多交点数的情况.就是第七条与前面六条都相交:1+2+3+4+5+6
八条最多交点数的情况.就是第八条与前面七条都相交:1+2+3+4+5+6+7
九条最多交点数的情况.就是第九条与前面八条都相交:1+2+3+4+5+6+7+8=36
当平面内的9条直线相交于同一点时,交点数最少,即n=1
则m+n=1+36=37
故选:B.
【点评】此题考查了平面图形,主要培养学生的观察能力和几何想象能力.
6.(2025 霍林郭勒市期末)在下列生活、生产现象中,可以用基本事实“两点确定一条直线”来解释的是( )
①用两颗钉子就可以把木条固定在墙上;
②把笔尖看成一个点,当这个点运动时便得到一条线;
③把弯曲的公路改直,就能缩短路程;
④植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上.
A.①③ B.②④ C.①④ D.②③
【考点】直线的性质:两点确定一条直线.
【专题】平移、旋转与对称;推理能力.
【答案】C
【分析】直接利用直线的性质以及线段的性质分析得出答案.
【解答】解:①用两颗钉子就可以把木条固定在墙上,可以用基本事实“两点确定一条直线”来解释;
②把笔尖看成一个点,当这个点运动时便得到一条线,可以用基本事实“无数个点组成线”来解释;
③把弯曲的公路改直,就能缩短路程,可以用基本事实“两点之间线段最短”来解释;
④植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上,可以用基本事实“两点确定一条直线”来解释.
故选:C.
【点评】此题主要考查了直线的性质以及线段的性质,正确把握相关性质是解题关键.
7.(2025 滨州)如图,OB是∠AOC的角平分线,OD是∠COE的角平分线,如果∠AOB=40°,∠COE=60°,则∠BOD的度数为( )
A.50° B.60° C.65° D.70°
【考点】角的计算;角平分线的定义.
【专题】计算题.
【答案】D
【分析】先根据OB是∠AOC的角平分线,OD是∠COE的角平分线,∠AOB=40°,∠COE=60°求出∠BOC与∠COD的度数,再根据∠BOD=∠BOC+∠COD即可得出结论.
【解答】解:∵OB是∠AOC的角平分线,OD是∠COE的角平分线,∠AOB=40°,∠COE=60°,
∴∠BOC=∠AOB=40°,∠COD∠COE60°=30°,
∴∠BOD=∠BOC+∠COD=40°+30°=70°.
故选:D.
【点评】本题考查的是角的计算,熟知角平分线的定义是解答此题的关键.
8.(2025 金华)如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是( )
A.两点确定一条直线
B.两点之间线段最短
C.垂线段最短
D.在同一平面内,过一点有且只有一条直线与已知直线垂直
【考点】直线的性质:两点确定一条直线.
【专题】应用题.
【答案】A
【分析】根据公理“两点确定一条直线”来解答即可.
【解答】解:经过刨平的木板上的两个点,能弹出一条笔直的墨线,此操作的依据是两点确定一条直线.
故选:A.
【点评】此题考查的是直线的性质在实际生活中的运用,此类题目有利于培养学生生活联系实际的能力.
9.(2025 西宁)如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°;③(∠α+∠β);④(∠α﹣∠β).正确的有( )
A.4个 B.3个 C.2个 D.1个
【考点】余角和补角.
【专题】压轴题.
【答案】B
【分析】根据角的性质,互补两角之和为180°,互余两角之和为90°,可将,①②③④中的式子化为含有∠α+∠β的式子,再将∠α+∠β=180°代入即可解出此题.
【解答】解:∵∠α和∠β互补,
∴∠α+∠β=180°.因为90°﹣∠β+∠β=90°,所以①正确;
又∠α﹣90°+∠β=∠α+∠β﹣90°=180°﹣90°=90°,②也正确;
(∠α+∠β)+∠β180°+∠β=90°+∠β≠90°,所以③错误;
(∠α﹣∠β)+∠β(∠α+∠β)180°=90°,所以④正确.
综上可知,①②④均正确.
故选:B.
【点评】本题考查了角之间互补与互余的关系,互补两角之和为180°,互余两角之和为90°.
10.(2024秋 管城区校级期末)如图,AE是一段高铁行驶路线图,图中字母表示的5个点表示5个车站在这段路线上往返行车,需印制( )种车票.
A.10 B.11 C.20 D.22
【考点】直线、射线、线段.
【专题】推理填空题;模型思想.
【答案】C
【分析】观察可以发现,每个车站作为起始站,可以到达除本站外的任何一个站,需要印制(5﹣1)种车票,而有5个起始站,故可以直接列出算式.
【解答】解:图中线段有AB,AC,AD,AE,BC,BD,BE,CD,CE,DE,共10条,单程要10种车票,往返就是20种,即5×(5﹣1)=20,
故选:C.
【点评】本题在线段的基础上,考查了排列与组合的知识,解题关键是要理解题意,每个车站都既可以作为起始站,可以到达除本站外的任何一个站.
二.填空题(共5小题)
11.(2024秋 芙蓉区校级期末)将一张长方形纸片按如图所示的方式折叠,BD、BE为折痕.若∠ABE=30°,则∠DBC为 60 度.
【考点】角的计算.
【专题】推理填空题;线段、角、相交线与平行线;推理能力.
【答案】见试题解答内容
【分析】根据折叠思想,通过角的和差计算即可求解.
【解答】解:∵BD、BE为折痕,∴BD、BE分别平分∠CBC′、∠ABA′
∴∠A′BE=∠ABE=30°,
∠DBC=∠DBC′
∵∠A′BE+∠ABE+∠DBC+∠DBC′=180°
∴∠ABE+∠DBC=90°
∴∠DBC=60°.
故答案为:60.
【点评】本题考查了角的计算,用正确角分线是解决本题的关键.
12.(2025 宁江区期末)长度12cm的线段AB的中点为M,C点将线段MB分成MC:CB=1:2,则线段AC的长度为 8cm .
【考点】比较线段的长短.
【专题】计算题.
【答案】见试题解答内容
【分析】先由中点的定义求出AM,BM的长,再根据MC:CB=1:2的关系,求MC的长,最后利用AC=AM+MC得其长度.
【解答】解:∵线段AB的中点为M,
∴AM=BM=6cm
设MC=x,则CB=2x,
∴x+2x=6,解得x=2
即MC=2cm.
∴AC=AM+MC=6+2=8cm.
【点评】利用中点性质转化线段之间的倍分关系是解题的关键,同时灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点.
13.(2025 麻栗坡县期末)如图是一个正方体的表面展开图,若正方体中相对的面上的数互为相反数,则2x﹣y的值为 ﹣3 .
【考点】专题:正方体相对两个面上的文字.
【专题】图表型.
【答案】见试题解答内容
【分析】根据正方体的展开图中相对面不存在公共点可找出5对面的数字,从而可根据相反数的定义求得x的值,进一步求得y的值,最后代入计算即可.
【解答】解:∵“5”与“2x﹣3”是对面,“x”与“y”是对面,
∴2x﹣3=﹣5,y=﹣x,
解得x=﹣1,y=1,
∴2x﹣y=﹣2﹣1=﹣3.
故答案为:﹣3.
【点评】本题主要考查的是正方体相对面上的文字,掌握正方体的展开图中相对面不存在公共点是解题的关键.
14.(2024春 路南区校级期末)如图,将三个同样的正方形的一个顶点重合放置,那么∠1的度数为 20° .
【考点】角的计算.
【专题】计算题.
【答案】见试题解答内容
【分析】根据∠1=∠BOD+EOC﹣∠BOE,利用正方形的角都是直角,即可求得∠BOD和∠EOC的度数从而求解.
【解答】解:∵∠BOD=90°﹣∠AOB=90°﹣30°=60°
∠EOC=90°﹣∠EOF=90°﹣40°=50°
又∵∠1=∠BOD+∠EOC﹣∠BOE
∴∠1=60°+50°﹣90°=20°
故答案为:20°.
【点评】本题主要考查了角度的计算,正确理解∠1=∠BOD+EOC﹣∠BOE这一关系是解决本题的关键.
15.(2025 巴南区校级期末)如图,已知∠COB=2∠AOC,OD平分∠AOB,且∠COD=20°,则∠AOB的度数为 120° .
【考点】角的计算;角平分线的定义.
【答案】见试题解答内容
【分析】根据角平分线的性质得出∠COB=2∠AOC=2x,∠AOD=∠BOD=1.5x,进而求出x的值,即可得出答案.
【解答】解:∵∠COB=2∠AOC,OD平分∠AOB,且∠COD=20°,
∴设∠COB=2∠AOC=2x,∠AOD=∠BOD=1.5x,
∴∠COD=0.5x=20°,
∴x=40°,
∴∠AOB的度数为:3×40°=120°.
故答案为:120°.
【点评】此题主要考查了角平分线的性质,根据题意得出∠COD=0.5x是解题关键.
三.解答题(共5小题)
16.(2024秋 城关区校级期末)如图,直线AB,CD相交于点O,OA平分∠EOC.
(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
【考点】角的计算.
【专题】计算题.
【答案】见试题解答内容
【分析】(1)根据角平分线定义得到∠AOC∠EOC70°=35°,然后根据对顶角相等得到∠BOD=∠AOC=35°;
(2)先设∠EOC=2x,∠EOD=3x,根据平角的定义得2x+3x=180°,解得x=36°,则∠EOC=2x=72°,然后与(1)的计算方法一样.
【解答】解:(1)∵OA平分∠EOC,
∴∠AOC∠EOC70°=35°,
∴∠BOD=∠AOC=35°;
(2)设∠EOC=2x,∠EOD=3x,根据题意得2x+3x=180°,解得x=36°,
∴∠EOC=2x=72°,
∴∠AOC∠EOC72°=36°,
∴∠BOD=∠AOC=36°.
【点评】考查了角的计算:1直角=90°;1平角=180°.也考查了角平分线的定义和对顶角的性质.
17.(2024 迎泽区校级开学)如图,已知线段AB和CD的公共部分BDABCD,线段AB、CD的中点E、F之间距离是10cm,求AB,CD的长.
【考点】两点间的距离.
【专题】方程思想.
【答案】见试题解答内容
【分析】先设BD=xcm,由题意得AB=3xcm,CD=4xcm,AC=6xcm,再根据中点的定义,用含x的式子表示出AE和CF,再根据EF=AC﹣AE﹣CF=2.5x,且E、F之间距离是10cm,所以2.5x=10,解方程求得x的值,即可求AB,CD的长.
【解答】解:设BD=xcm,则AB=3xcm,CD=4xcm,AC=6xcm.
∵点E、点F分别为AB、CD的中点,∴AEAB=1.5xcm,CFCD=2xcm.
∴EF=AC﹣AE﹣CF=6x﹣1.5x﹣2x=2.5xcm.∵EF=10cm,∴2.5x=10,解得:x=4.
∴AB=12cm,CD=16cm.
【点评】本题主要考查了两点间的距离和中点的定义,注意运用数形结合思想和方程思想.
18.(2024秋 恩施市期末)【背景知识】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点A、点B表示的数分别为a、b,则A,B两点之间的距离AB=|a﹣b|,线段AB的中点表示的数为.
【问题情境】如图,数轴上点A表示的数为﹣2,点B表示的数为8,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
【综合运用】
(1)填空:
①A、B两点间的距离AB= 10 ,线段AB的中点表示的数为 3 ;
②用含t的代数式表示:t秒后,点P表示的数为 ﹣2+3t ;点Q表示的数为 8﹣2t .
(2)求当t为何值时,P、Q两点相遇,并写出相遇点所表示的数;
(3)求当t为何值时,PQAB;
(4)若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.
【考点】两点间的距离;数轴;绝对值;一元一次方程的应用.
【答案】见试题解答内容
【分析】(1)根据题意即可得到结论;
(2)当P、Q两点相遇时,P、Q表示的数相等列方程得到t=2,于是得到当t=2时,P、Q相遇,即可得到结论;
(3)由t秒后,点P表示的数﹣2+3t,点Q表示的数为8﹣2t,于是得到PQ=|(﹣2+3t)﹣(8﹣2t)|=|5t﹣10|,列方程即可得到结论;
(4)由点M表示的数为 2,点N表示的数为 3,即可得到结论.
【解答】解:(1)①10,3;
②﹣2+3t,8﹣2t;
(2)∵当P、Q两点相遇时,P、Q表示的数相等
∴﹣2+3t=8﹣2t,
解得:t=2,
∴当t=2时,P、Q相遇,
此时,﹣2+3t=﹣2+3×2=4,
∴相遇点表示的数为4;
(3)∵t秒后,点P表示的数﹣2+3t,点Q表示的数为8﹣2t,
∴PQ=|(﹣2+3t)﹣(8﹣2t)|=|5t﹣10|,
又PQAB10=5,
∴|5t﹣10|=5,
解得:t=1或3,
∴当:t=1或3时,PQAB;
(4)不变.
∵点M表示的数为 2,
点N表示的数为 3,
∴MN=|(2)﹣(3)|=|23|=5.
【点评】本题考查了一元一次方程的应用和数轴,解题的关键是掌握点的移动与点所表示的数之间的关系,根据题目给出的条件,找出合适的等量关系列出方程,再求解.
19.(2025 五华县期末)如图,OM是∠AOC的平分线,ON是∠BOC的平分线.
(1)如图1,当∠AOB是直角,∠BOC=60°时,∠MON的度数是多少?
(2)如图2,当∠AOB=α,∠BOC=60°时,猜想∠MON与α的数量关系;
(3)如图3,当∠AOB=α,∠BOC=β时,猜想∠MON与α、β有数量关系吗?如果有,指出结论并说明理由.
【考点】角的计算;角平分线的定义.
【答案】见试题解答内容
【分析】(1)求出∠AOC度数,求出∠MOC和∠NOC的度数,代入∠MON=∠MOC﹣∠NOC求出即可;
(2)求出∠AOC度数,求出∠MOC和∠NOC的度数,代入∠MON=∠MOC﹣∠NOC求出即可;
(3)求出∠AOC度数,求出∠MOC和∠NOC的度数,代入∠MON=∠MOC﹣∠NOC求出即可.
【解答】解:(1)如图1,∵∠AOB=90°,∠BOC=60°,
∴∠AOC=90°+60°=150°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC∠AOC=75°,∠NOC∠BOC=30°
∴∠MON=∠MOC﹣∠NOC=45°.
(2)如图2,∠MONα,
理由是:∵∠AOB=α,∠BOC=60°,
∴∠AOC=α+60°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC∠AOCα+30°,∠NOC∠BOC=30°
∴∠MON=∠MOC﹣∠NOC=(α+30°)﹣30°α.
(3)如图3,∠MONα,与β的大小无关.
理由:∵∠AOB=α,∠BOC=β,
∴∠AOC=α+β.
∵OM是∠AOC的平分线,ON是∠BOC的平分线,
∴∠MOC∠AOC(α+β),
∠NOC∠BOCβ,
∴∠MON=∠MOC﹣∠NOC
(α+β)β
α
即∠MONα.
【点评】本题考查了角平分线定义和角的有关计算,关键是求出∠AOC、∠MOC、∠NOC的度数和得出∠MON=∠MOC﹣∠NOC.
20.(2025 青云谱区期末)已知点C在线段AB上,AC=2BC,点D、E在直线AB上,点D在点E的左侧.
(1)若AB=18,DE=8,线段DE在线段AB上移动.
①如图1,当E为BC中点时,求AD的长;
②点F(异于A,B,C点)在线段AB上,AF=3AD,CE+EF=3,求AD的长;
(2)若AB=2DE,线段DE在直线AB上移动,且满足关系式,则 或 .
【考点】两点间的距离.
【专题】压轴题;线段、角、相交线与平行线;运算能力;推理能力.
【答案】见试题解答内容
【分析】(1)根据AC=2BC,AB=18,DE=8,线段DE在线段AB上移动.
①如图1,当E为BC中点时,根据中点定义即可求AD的长;
②点F(异于A,B,C点)在线段AB上,AF=3AD,CE+EF=3,确定点F是BC的中点,即可求AD的长;
(2)根据AC=2BC,AB=2DE,线段DE在直线AB上移动,满足关系式,可以设CE=x,DC=y,用含x和y的式子表示线段长,从而得出x与y的等量关系,即可求出的值.
【解答】解:(1)AC=2BC,AB=18,DE=8,
∴BC=6,AC=12,
①如图,
∵E为BC中点,
∴CE=3,
∴CD=5,
∴AD=AB﹣DB=18﹣11=7;
②如图,
Ⅰ、当点E在点F的左侧,
∵CE+EF=3,BC=6,
∴点F是BC的中点,
∴CF=BF=3,
∴AF=AB﹣BF=18﹣3=15,
∴ADAF=5;
Ⅱ、当点E在点F的右侧,
∵AC=12,CE+EF=CF=3,
∴AF=AC﹣CF=9,
∴AF=3AD=9,
∴AD=3.
其他情况不存在,舍去.
综上所述:AD的长为3或5;
(2)∵AC=2BC,AB=2DE,满足关系式,
Ⅰ、当点E在点C右侧时,如图,
设CE=x,DC=y,
则DE=x+y,
∴AB=2(x+y)
ACAB(x+y)
∴AD=AC﹣DCxy
BCAB(x+y)
∴BE=BC﹣CEyx
∴AD+ECxy
∵2(AD+EC)=3BE
∴2(xy)=3(yx)
解得,17x=4y,
∴.
Ⅱ、当点E在点A左侧时,如图,
设CE=x,DC=y,
则DE=y﹣x,
∴AB=2(y﹣x)
ACAB(y﹣x)
∴AD=DC﹣ACxy
BCAB(y﹣x)
∴BE=BC+CEyx
∴AD+ECxy
∵2(AD+EC)=3BE
∴2(xy)=3(yx)
解得,11x=8y,
∴.
点D在C点右侧,及点D在B点右侧,
无解,不符合题意;
当DE在线段AC内部时,如图,
设CE=x,DC=y,
则DE=y﹣x,
∴AB=2(y﹣x),
ACAB(y﹣x),
∴AD=AC﹣DCyx,
BCAB(y﹣x),
∴BE=BC+CEyx,
∴AD+ECxy,
∵2(AD+EC)=3BE
∴2(xy)=3(yx),
解得,﹣5x=4y(不符合题意,舍去),
∴,不符合题意,舍去.
其他情况不存在,舍去.
故答案为或.
【点评】本题考查了两点间的距离,比较难,需要仔细思考和解答.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
