2026年中考数学一轮复习 一元二次方程(含解析)
文档属性
| 名称 | 2026年中考数学一轮复习 一元二次方程(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 205.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 05:37:43 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中考数学一轮复习 一元二次方程
一.选择题(共10小题)
1.(2025春 蜀山区校级期中)关于x的一元二次方程(a﹣1)x2+x+a2﹣1=0的一个根是0,则a的值为( )
A.1 B.﹣1 C.1或﹣1 D.
2.(2025 枣庄)若关于x的一元二次方程x2﹣2x+kb+1=0有两个不相等的实数根,则一次函数y=kx+b的大致图象可能是( )
A. B.
C. D.
3.(2025 桂林)若关于x的一元二次方程(k﹣1)x2+4x+1=0有两个不相等的实数根,则k的取值范围是( )
A.k<5 B.k<5,且k≠1 C.k≤5,且k≠1 D.k>5
4.(2025 安顺)一个等腰三角形的两条边长分别是方程x2﹣7x+10=0的两根,则该等腰三角形的周长是( )
A.12 B.9 C.13 D.12或9
5.(2025 江北区期末)对于一元二次方程ax2+bx+c=0(a≠0),下列说法:
①若a+b+c=0,则b2﹣4ac≥0;
②若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
③若c是方程ax2+bx+c=0的一个根,则一定有ac+b+1=0成立;
④若x0是一元二次方程ax2+bx+c=0的根,则
⑤存在实数m、n(m≠n),使得am2+bm+c=an2+bn+c;
其中正确的( )
A.只有①②④ B.只有①②④⑤ C.①②③④⑤ D.只有①②③
6.(2025 武进区校级自主招生)设关于x的方程ax2+(a+2)x+9a=0,有两个不相等的实数根x1、x2,且x1<1<x2,那么实数a的取值范围是( )
A. B. C. D.
7.(2025 呼伦贝尔)某种品牌运动服经过两次降价,每件零售价由560元降为315元,已知两次降价的百分率相同,求每次降价的百分率.设每次降价的百分率为x,下面所列的方程中正确的是( )
A.560(1+x)2=315 B.560(1﹣x)2=315
C.560(1﹣2x)2=315 D.560(1﹣x2)=315
8.(2025 深圳模拟)已知α、β是方程x2﹣2x﹣4=0的两个实数根,则α3+8β+6的值为( )
A.﹣1 B.2 C.22 D.30
9.(2024秋 贵州期末)把方程x(x+2)=5(x﹣2)化成一般式,则a、b、c的值分别是( )
A.1,﹣3,10 B.1,7,﹣10 C.1,﹣5,12 D.1,3,2
10.(2025 广州)已知2是关于x的方程x2﹣2mx+3m=0的一个根,并且这个方程的两个根恰好是等腰三角形ABC的两条边长,则三角形ABC的周长为( )
A.10 B.14 C.10或14 D.8或10
二.填空题(共5小题)
11.(2025 海曙区自主招生)如果方程(x﹣1)(x2﹣2x)=0的三根可以作为一个三角形的三边之长,那么实数k的取值范围是 .
12.(2025 沂源县一模)如果恰好只有一个实数a是方程(k2﹣9)x2﹣2(k+1)x+1=0的根,则k的值为 .
13.(2025 临沂)对于实数a,b,定义运算“*”:a*b.例如4*2,因为4>2,所以4*2=42﹣4×2=8.若x1,x2是一元二次方程x2﹣5x+6=0的两个根,则x1*x2= .
14.(2025 温江区校级自主招生)若关于x的方程(1﹣m2)x2+2mx﹣1=0的所有根都是比1小的正实数,则实数m的取值范围是 .
15.(2025 贵阳)如图,在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高.动点P从点A出发,沿A→D方向以cm/s的速度向点D运动.设△ABP的面积为S1,矩形PDFE的面积为S2,运动时间为t秒(0<t<8),则t= 秒时,S1=2S2.
三.解答题(共5小题)
16.(2025 湖北)如图,一农户要建一个矩形猪舍,猪舍的一边利用长为12m的住房墙,另外三边用25m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,所围矩形猪舍的长、宽分别为多少时,猪舍面积为80m2?
17.(2025 淮安)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
18.(2024秋 定安县校级月考)如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2cm/s的速度向D移动.
(1)P、Q两点从出发开始到几秒时,四边形PBCQ的面积为33cm2;
(2)P、Q两点从出发开始到几秒时,点P和点Q的距离是10cm.
19.(2025 北京)关于x的一元二次方程x2﹣(k+3)x+2k+2=0.
(1)求证:方程总有两个实数根;
(2)若方程有一个根小于1,求k的取值范围.
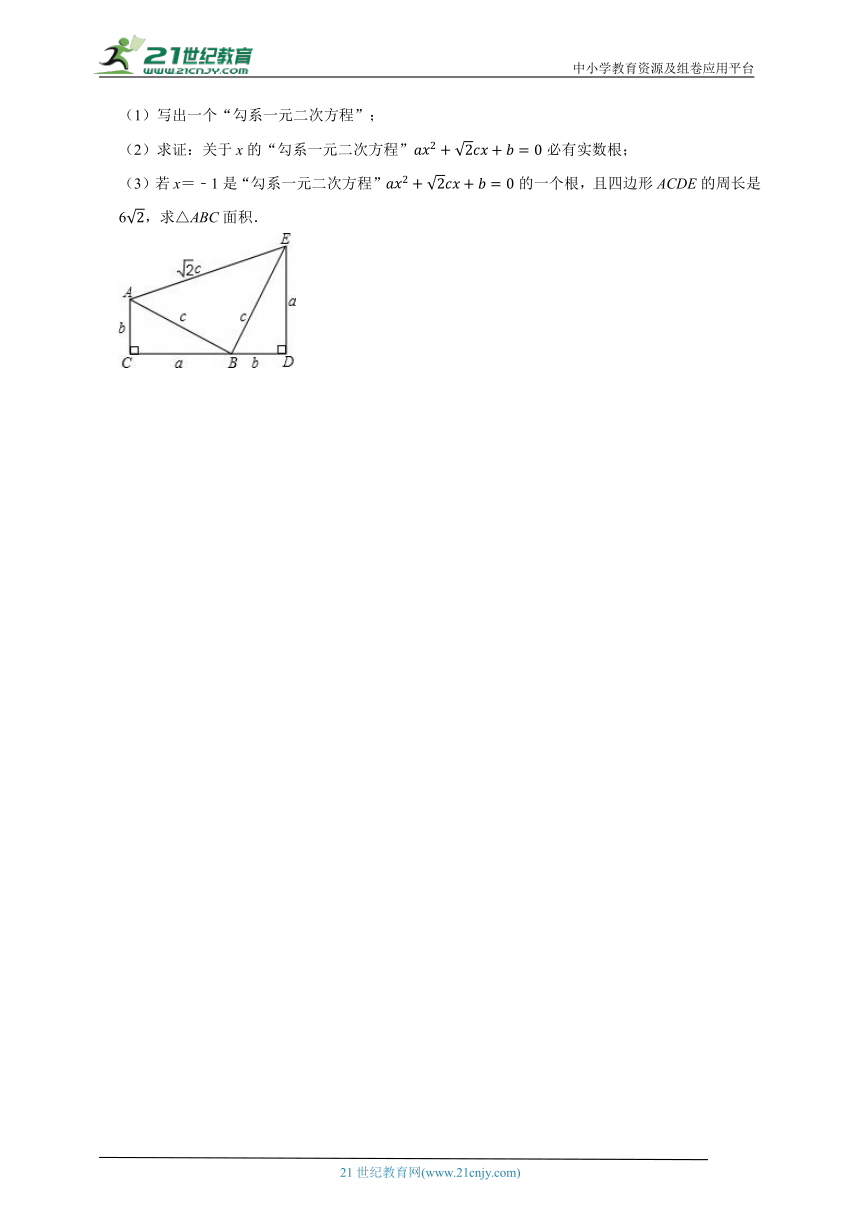
20.(2025 濉溪县三模)如图,四边形ACDE是证明勾股定理时用到的一个图形,a,b,c是Rt△ABC和Rt△BED边长,易知,这时我们把关于x的形如的一元二次方程称为“勾系一元二次方程”.
请解决下列问题:
(1)写出一个“勾系一元二次方程”;
(2)求证:关于x的“勾系一元二次方程”必有实数根;
(3)若x=﹣1是“勾系一元二次方程”的一个根,且四边形ACDE的周长是6,求△ABC面积.
中考数学一轮复习 一元二次方程
参考答案与试题解析
一.选择题(共10小题)
1.(2025春 蜀山区校级期中)关于x的一元二次方程(a﹣1)x2+x+a2﹣1=0的一个根是0,则a的值为( )
A.1 B.﹣1 C.1或﹣1 D.
【考点】一元二次方程的解.
【专题】符号意识;应用意识.
【答案】B
【分析】根据方程的解的定义,把x=0代入方程,即可得到关于a的方程,再根据一元二次方程的定义即可求解.
【解答】解:根据题意得:a2﹣1=0且a﹣1≠0,
解得:a=﹣1.
故选:B.
【点评】本题主要考查了一元二次方程的解的定义,特别需要注意的条件是二次项系数不等于0.
2.(2025 枣庄)若关于x的一元二次方程x2﹣2x+kb+1=0有两个不相等的实数根,则一次函数y=kx+b的大致图象可能是( )
A. B.
C. D.
【考点】根的判别式;一次函数的图象.
【答案】B
【分析】根据一元二次方程x2﹣2x+kb+1=0有两个不相等的实数根,得到判别式大于0,求出kb的符号,对各个图象进行判断即可.
【解答】解:∵x2﹣2x+kb+1=0有两个不相等的实数根,
∴Δ=4﹣4(kb+1)>0,
解得kb<0,
A.k>0,b>0,即kb>0,故A不正确;
B.k>0,b<0,即kb<0,故B正确;
C.k<0,b<0,即kb>0,故C不正确;
D.k<0,b=0,即kb=0,故D不正确;
故选:B.
【点评】本题考查的是一元二次方程根的判别式和一次函数的图象,一元二次方程根的情况与判别式△的关系:(1)Δ>0 方程有两个不相等的实数根;(2)Δ=0 方程有两个相等的实数根;(3)Δ<0 方程没有实数根.
3.(2025 桂林)若关于x的一元二次方程(k﹣1)x2+4x+1=0有两个不相等的实数根,则k的取值范围是( )
A.k<5 B.k<5,且k≠1 C.k≤5,且k≠1 D.k>5
【考点】根的判别式;一元二次方程的定义.
【答案】B
【分析】根据方程为一元二次方程且有两个不相等的实数根,结合一元二次方程的定义以及根的判别式即可得出关于k的一元一次不等式组,解不等式组即可得出结论.
【解答】解:∵关于x的一元二次方程(k﹣1)x2+4x+1=0有两个不相等的实数根,
∴,即,
解得:k<5且k≠1.
故选:B.
【点评】本题考查了根的判别式以及一元二次方程的定义,解题的关键是得出关于k的一元一次不等式组.本题属于基础题,难度不大,解决该题型题目时,根据方程根的个数结合一元二次方程的定义以及根的判别式得出不等式组是关键.
4.(2025 安顺)一个等腰三角形的两条边长分别是方程x2﹣7x+10=0的两根,则该等腰三角形的周长是( )
A.12 B.9 C.13 D.12或9
【考点】解一元二次方程﹣因式分解法;三角形三边关系;等腰三角形的性质.
【答案】A
【分析】求出方程的解,即可得出三角形的边长,再求出即可.
【解答】解:x2﹣7x+10=0,
(x﹣2)(x﹣5)=0,
x﹣2=0,x﹣5=0,
x1=2,x2=5,
①等腰三角形的三边是2,2,5
∵2+2<5,
∴不符合三角形三边关系定理,此时不符合题意;
②等腰三角形的三边是2,5,5,此时符合三角形三边关系定理,三角形的周长是2+5+5=12;
即等腰三角形的周长是12.
故选:A.
【点评】本题考查了等腰三角形性质、解一元二次方程、三角形三边关系定理的应用等知识,关键是求出三角形的三边长.
5.(2025 江北区期末)对于一元二次方程ax2+bx+c=0(a≠0),下列说法:
①若a+b+c=0,则b2﹣4ac≥0;
②若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
③若c是方程ax2+bx+c=0的一个根,则一定有ac+b+1=0成立;
④若x0是一元二次方程ax2+bx+c=0的根,则
⑤存在实数m、n(m≠n),使得am2+bm+c=an2+bn+c;
其中正确的( )
A.只有①②④ B.只有①②④⑤ C.①②③④⑤ D.只有①②③
【考点】根的判别式.
【专题】压轴题;判别式法;一元二次方程及应用;运算能力;推理能力.
【答案】B
【分析】按照方程的解的含义、一元二次方程的实数根与判别式的关系、等式的性质、一元二次方程的求根公式等对各选项分别讨论,可得答案.
【解答】解:①若a+b+c=0,则x=1是方程ax2+bx+c=0的解,
由一元二次方程的实数根与判别式的关系可知Δ=b2﹣4ac≥0,故①正确;
②∵方程ax2+c=0有两个不相等的实根,
∴Δ=0﹣4ac>0,
∴﹣4ac>0,
则方程ax2+bx+c=0的判别式Δ=b2﹣4ac>0,
∴方程ax2+bx+c=0必有两个不相等的实根,故②正确;
③∵c是方程ax2+bx+c=0的一个根,
则ac2+bc+c=0,
∴c(ac+b+1)=0,
若c=0,等式仍然成立,
但ac+b+1=0不一定成立,故③不正确;
④若x0是一元二次方程ax2+bx+c=0的根,
则由求根公式可得:
x0或x0
∴2ax0+b或2ax0+b
∴
故④正确.
⑤存在实数m、n(m≠n),使得am2+bm+c=an2+bn+c成立;
∵由am2+bm+c=an2+bn+c,
∴a(m2﹣n2)+b(m﹣n)=0,
∴a(m﹣n)(m+n)+b(m﹣n)=0,
即(m﹣n)[a(m+n)+b]=0,
∵m≠n,
∴a(m+n)+b=0,
∴当a≠0时,存在实数m、n(m≠n),使得am2+bm+c=an2+bn+c成立;
故⑤正确.
故选:B.
【点评】本题主要考查了一元二次方程的实数根与判别式的关系,牢固掌握二者的关系并灵活运用,是解题的关键.
6.(2025 武进区校级自主招生)设关于x的方程ax2+(a+2)x+9a=0,有两个不相等的实数根x1、x2,且x1<1<x2,那么实数a的取值范围是( )
A. B. C. D.
【考点】根与系数的关系;根的判别式.
【专题】转化思想.
【答案】D
【分析】方法1、根据一元二次方程的根的判别式,建立关于a的不等式,求出a的取值范围.又存在x1<1<x2,即(x1﹣1)(x2﹣1)<0,x1x2﹣(x1+x2)+1<0,利用根与系数的关系,从而最后确定a的取值范围.
方法2、由方程有两个实数根即可得出此方程是一元二次方程,而x1<1<x2,可以看成是二次函数y=ax2+(a+2)x+9a的图象与x轴的两个交点在1左右两侧,由此得出自变量x=1时,对应的函数值的符号,即可得出结论.
【解答】解:方法1、∵方程有两个不相等的实数根,
则a≠0且Δ>0,
由(a+2)2﹣4a×9a=﹣35a2+4a+4>0,
解得a,
∵x1+x2,x1x2=9,
又∵x1<1<x2,
∴x1﹣1<0,x2﹣1>0,
那么(x1﹣1)(x2﹣1)<0,
∴x1x2﹣(x1+x2)+1<0,
即91<0,
解得a<0,
最后a的取值范围为:a<0.
故选D.
方法2、由题意知,a≠0,令y=ax2+(a+2)x+9a,
由于方程的两根一个大于1,一个小于1,
∴抛物线与x轴的交点分别在1两侧,
当a>0时,x=1时,y<0,
∴a+(a+2)+9a<0,
∴a(不符合题意,舍去),
当a<0时,x=1时,y>0,
∴a+(a+2)+9a>0,
∴a,
∴a<0,
故选:D.
【点评】总结:1、一元二次方程根的情况与判别式△的关系:
(1)Δ>0 方程有两个不相等的实数根;
(2)Δ=0 方程有两个相等的实数根;
(3)Δ<0 方程没有实数根.
2、根与系数的关系为:x1+x2,x1x2.
7.(2025 呼伦贝尔)某种品牌运动服经过两次降价,每件零售价由560元降为315元,已知两次降价的百分率相同,求每次降价的百分率.设每次降价的百分率为x,下面所列的方程中正确的是( )
A.560(1+x)2=315 B.560(1﹣x)2=315
C.560(1﹣2x)2=315 D.560(1﹣x2)=315
【考点】由实际问题抽象出一元二次方程.
【专题】增长率问题.
【答案】B
【分析】设每次降价的百分率为x,根据降价后的价格=降价前的价格(1﹣降价的百分率),则第一次降价后的价格是560(1﹣x),第二次降价后的价格是560(1﹣x)2,据此即可列方程求解.
【解答】解:设每次降价的百分率为x,由题意得:
560(1﹣x)2=315,
故选:B.
【点评】此题主要考查了由实际问题抽象出一元二次方程,关键是根据题意找到等式两边的平衡条件,这种价格问题主要解决价格变化前后的平衡关系,列出方程即可.
8.(2025 深圳模拟)已知α、β是方程x2﹣2x﹣4=0的两个实数根,则α3+8β+6的值为( )
A.﹣1 B.2 C.22 D.30
【考点】一元二次方程的解.
【专题】计算题.
【答案】D
【分析】根据根与系数的关系得到α+β=2,由一元二次方程解的定义得到α2﹣2α﹣4=0,则α2=2α+4,然后将其代入所求的代数式,并求值.
【解答】解:∵α、β是方程x2﹣2x﹣4=0的两个实数根,
∴α+β=2,α2﹣2α﹣4=0,
∴α2=2α+4
∴α3+8β+6=α α2+8β+6
=α (2α+4)+8β+6
=2α2+4α+8β+6
=2(2α+4)+4α+8β+6
=8α+8β+14
=8(α+β)+14=30,
故选:D.
【点评】本题主要考查了一元二次方程的解.解答本题时,利用根与系数得到α+β=2,α2﹣2α﹣4=0是解题的关键.
9.(2024秋 贵州期末)把方程x(x+2)=5(x﹣2)化成一般式,则a、b、c的值分别是( )
A.1,﹣3,10 B.1,7,﹣10 C.1,﹣5,12 D.1,3,2
【考点】一元二次方程的一般形式.
【专题】推理填空题;一元二次方程及应用.
【答案】A
【分析】a、b、c分别指的是一元二次方程的一般式中的二次项系数、一次项系数、常数项.
【解答】解:由方程x(x+2)=5(x﹣2),得
x2﹣3x+10=0,
∴a、b、c的值分别是1、﹣3、10;
故选:A.
【点评】本题考查了一元二次方程的一般形式.一元二次方程的一般形式是:ax2+bx+c=0(a,b,c是常数且a≠0),在一般形式中ax2叫二次项,bx叫一次项,c是常数项.其中a,b,c分别叫二次项系数,一次项系数,常数项.
10.(2025 广州)已知2是关于x的方程x2﹣2mx+3m=0的一个根,并且这个方程的两个根恰好是等腰三角形ABC的两条边长,则三角形ABC的周长为( )
A.10 B.14 C.10或14 D.8或10
【考点】解一元二次方程﹣因式分解法;三角形三边关系;等腰三角形的性质;一元二次方程的解.
【答案】B
【分析】先将x=2代入x2﹣2mx+3m=0,求出m=4,则方程即为x2﹣8x+12=0,利用因式分解法求出方程的根x1=2,x2=6,分两种情况:①当6是腰时,2是底边;②当6是底边时,2是腰进行讨论.注意两种情况都要用三角形三边关系定理进行检验.
【解答】解:∵2是关于x的方程x2﹣2mx+3m=0的一个根,
∴22﹣4m+3m=0,m=4,
∴x2﹣8x+12=0,
解得x1=2,x2=6.
①当6是腰时,2是底边,此时周长=6+6+2=14;
②当6是底边时,2是腰,2+2<6,不能构成三角形.
所以它的周长是14.
故选:B.
【点评】此题主要考查了一元二次方程的解,解一元二次方程﹣因式分解法,三角形三边关系定理以及等腰三角形的性质,注意求出三角形的三边后,要用三边关系定理检验.
二.填空题(共5小题)
11.(2025 海曙区自主招生)如果方程(x﹣1)(x2﹣2x)=0的三根可以作为一个三角形的三边之长,那么实数k的取值范围是 3<k≤4 .
【考点】根与系数的关系;三角形三边关系;根的判别式.
【专题】压轴题.
【答案】见试题解答内容
【分析】根据原方程可得出:①x﹣1=0,②x2﹣2x0;根据根与系数的关系,可求出②方程的x1+x2和x1﹣x2的表达式,然后根据三角形三边关系定理求出k的取值范围.
【解答】解:由题意,得:x﹣1=0,x2﹣2x0;
设x2﹣2x0的两根分别是m、n(m≥n);则m+n=2,mn;
m﹣n;
根据三角形三边关系定理,得:
m﹣n<1<m+n,即1<2;
∴,解得3<k≤4.
【点评】此题主要考查的是一元二次方程根与系数的关系以及三角形三边关系定理.
12.(2025 沂源县一模)如果恰好只有一个实数a是方程(k2﹣9)x2﹣2(k+1)x+1=0的根,则k的值为 ±3或﹣5 .
【考点】根的判别式.
【专题】计算题.
【答案】见试题解答内容
【分析】分原方程是一元一次方程和一元二次方程两种情况讨论即可得到答案.
【解答】解:①当原方程是一个一元一次方程时,方程只有一个实数根,
则k2﹣9=0,
解得k=±3,
②如果方程是一元二次方程时,则方程有两个相等的实数根,
即Δ=b2﹣4ac=0,
即:4(k+1)2﹣4(k2﹣9)=0
解得:k=﹣5.
故答案为±3或﹣5.
【点评】本题考查了根的判别式,同时还考查了分类讨论思想,是一道好题.
13.(2025 临沂)对于实数a,b,定义运算“*”:a*b.例如4*2,因为4>2,所以4*2=42﹣4×2=8.若x1,x2是一元二次方程x2﹣5x+6=0的两个根,则x1*x2= 3或﹣3 .
【考点】解一元二次方程﹣因式分解法.
【专题】压轴题;新定义.
【答案】见试题解答内容
【分析】首先解方程x2﹣5x+6=0,再根据a*b,求出x1*x2的值即可.
【解答】解:∵x1,x2是一元二次方程x2﹣5x+6=0的两个根,
∴(x﹣3)(x﹣2)=0,
解得:x=3或2,
①当x1=3,x2=2时,x1*x2=32﹣3×2=3;
②当x1=2,x2=3时,x1*x2=3×2﹣32=﹣3.
故答案为:3或﹣3.
【点评】此题主要考查了因式分解法解一元二次方程以及利用材料分析解决新问题,根据已知进行分类讨论是解题关键.
14.(2025 温江区校级自主招生)若关于x的方程(1﹣m2)x2+2mx﹣1=0的所有根都是比1小的正实数,则实数m的取值范围是 m=1或m>2 .
【考点】根与系数的关系.
【专题】分类讨论.
【答案】见试题解答内容
【分析】分1﹣m2=0,1﹣m2≠0两种情况先求出原方程的实数根,再根据两个实数根都是比1小的正实数,列出不等式,求出m的取值范围.
【解答】解:当1﹣m2=0时,m=±1.
当m=1时,可得2x﹣1=0,x,符合题意;
当m=﹣1时,可得﹣2x﹣1=0,x,不符合题意;
当1﹣m2≠0时,(1﹣m2)x2+2mx﹣1=0,
[(1+m)x﹣1][(1﹣m)x+1]=0,
∴x1,x2.
∵关于x的方程(1﹣m2)x2+2mx﹣1=0的所有根都是比1小的正实数,
∴01,解得m>0,
01,解得m>2.
综上可得,实数m的取值范围是m=1或m>2.
故答案为:m=1或m>2.
【点评】考查了解一元二次方程及解一元一次不等式,解题的关键是将二次项系数分1﹣m2=0,1﹣m2≠0两种情况讨论求解.
15.(2025 贵阳)如图,在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高.动点P从点A出发,沿A→D方向以cm/s的速度向点D运动.设△ABP的面积为S1,矩形PDFE的面积为S2,运动时间为t秒(0<t<8),则t= 6 秒时,S1=2S2.
【考点】一元二次方程的应用;等腰直角三角形;矩形的性质.
【专题】几何动点问题;压轴题.
【答案】见试题解答内容
【分析】利用三角形的面积公式以及矩形的面积公式,表示出S1和S2,然后根据S1=2S2,即可列方程求解.
【解答】解:∵Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高,
∴AD=BD=CD=8cm,
又∵APt,
则S1AP BD8t=8t,PD=8t,
∵PE∥BC,
∴△APE∽△ADC,
∴,
∴PE=APt,
∴S2=PD PE=(8t) t,
∵S1=2S2,
∴8t=2(8t) t,
解得:t=6.
故答案为:6.
【点评】本题考查了一元二次方程的应用,以及等腰直角三角形的性质,正确表示出S1和S2是关键.
三.解答题(共5小题)
16.(2025 湖北)如图,一农户要建一个矩形猪舍,猪舍的一边利用长为12m的住房墙,另外三边用25m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,所围矩形猪舍的长、宽分别为多少时,猪舍面积为80m2?
【考点】一元二次方程的应用.
【专题】几何图形问题.
【答案】见试题解答内容
【分析】设矩形猪舍垂直于住房墙一边长为x m可以得出平行于墙的一边的长为(25﹣2x+1)m.根据矩形的面积公式建立方程求出其解就可以了.
【解答】解:设矩形猪舍垂直于住房墙一边长为x m可以得出平行于墙的一边的长为(25﹣2x+1)m,由题意得
x(25﹣2x+1)=80,
化简,得x2﹣13x+40=0,
解得:x1=5,x2=8,
当x=5时,26﹣2x=16>12(舍去),当x=8时,26﹣2x=10<12,
答:所围矩形猪舍的长为10m、宽为8m.
【点评】本题考查了列一元二次方程解实际问题的运用,矩形的面积公式的运用及一元二次方程的解法的运用,解答时寻找题目的等量关系是关键.
17.(2025 淮安)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 (100+200x) 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
【考点】一元二次方程的应用.
【专题】销售问题.
【答案】见试题解答内容
【分析】(1)销售量=原来销售量+下降销售量,据此列式即可;
(2)根据销售量×每斤利润=总利润列出方程求解即可.
【解答】解:(1)将这种水果每斤的售价降低x元,则每天的销售量是10020=(100+200x)(斤);
(2)根据题意得:(4﹣2﹣x)(100+200x)=300,
解得:x或x=1,
当x时,销售量是100+200200<260;
当x=1时,销售量是100+200=300(斤).
∵每天至少售出260斤,
∴x=1.
答:张阿姨需将每斤的售价降低1元.
【点评】本题考查理解题意的能力,第一问关键求出每千克的利润,求出总销售量,从而利润.第二问,根据售价和销售量的关系,以利润作为等量关系列方程求解.
18.(2024秋 定安县校级月考)如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2cm/s的速度向D移动.
(1)P、Q两点从出发开始到几秒时,四边形PBCQ的面积为33cm2;
(2)P、Q两点从出发开始到几秒时,点P和点Q的距离是10cm.
【考点】一元二次方程的应用.
【专题】几何动点问题;压轴题.
【答案】见试题解答内容
【分析】(1)设P、Q两点从出发开始到x秒时四边形PBCQ的面积为33cm2,则PB=(16﹣3x)cm,QC=2xcm,根据梯形的面积公式可列方程:(16﹣3x+2x)×6=33,解方程可得解;
(2)作QE⊥AB,垂足为E,设运动时间为t秒,用t表示线段长,用勾股定理列方程求解.
【解答】解:(1)设P、Q两点从出发开始到x秒时四边形PBCQ的面积为33cm2,
则PB=(16﹣3x)cm,QC=2xcm,
根据梯形的面积公式得(16﹣3x+2x)×6=33,
解之得x=5,
(2)设P,Q两点从出发经过t秒时,点P,Q间的距离是10cm,
作QE⊥AB,垂足为E,
则QE=AD=6,PQ=10,
∵PA=3t,CQ=BE=2t,
∴PE=AB﹣AP﹣BE=|16﹣5t|,
由勾股定理,得(16﹣5t)2+62=102,
解得t1=4.8,t2=1.6.
答:(1)P、Q两点从出发开始到5秒时四边形PBCQ的面积为33cm2;
(2)从出发到1.6秒或4.8秒时,点P和点Q的距离是10cm.
【点评】(1)主要用到了梯形的面积公式:S(上底+下底)×高;(2)作辅助线是关键,构成直角三角形后,用了勾股定理.
19.(2025 北京)关于x的一元二次方程x2﹣(k+3)x+2k+2=0.
(1)求证:方程总有两个实数根;
(2)若方程有一个根小于1,求k的取值范围.
【考点】根的判别式.
【答案】见试题解答内容
【分析】(1)根据方程的系数结合根的判别式,可得Δ=(k﹣1)2≥0,由此可证出方程总有两个实数根;
(2)利用分解因式法解一元二次方程,可得出x1=2、x2=k+1,根据方程有一根小于1,即可得出关于k的一元一次不等式,解之即可得出k的取值范围.
【解答】(1)证明:∵在方程x2﹣(k+3)x+2k+2=0中,Δ=[﹣(k+3)]2﹣4×1×(2k+2)=k2﹣2k+1=(k﹣1)2≥0,
∴方程总有两个实数根.
(2)解:∵x2﹣(k+3)x+2k+2=(x﹣2)(x﹣k﹣1)=0,
∴x1=2,x2=k+1.
∵方程有一根小于1,
∴k+1<1,解得:k<0,
∴k的取值范围为k<0.
【点评】本题考查了根的判别式、因式分解法解一元二次方程以及解一元一次不等式,解题的关键是:(1)牢记“当△≥0时,方程有两个实数根”;(2)利用因式分解法解一元二次方程结合方程一根小于1,找出关于k的一元一次不等式.
20.(2025 濉溪县三模)如图,四边形ACDE是证明勾股定理时用到的一个图形,a,b,c是Rt△ABC和Rt△BED边长,易知,这时我们把关于x的形如的一元二次方程称为“勾系一元二次方程”.
请解决下列问题:
(1)写出一个“勾系一元二次方程”;
(2)求证:关于x的“勾系一元二次方程”必有实数根;
(3)若x=﹣1是“勾系一元二次方程”的一个根,且四边形ACDE的周长是6,求△ABC面积.
【考点】一元二次方程的应用;勾股定理的证明.
【专题】几何图形问题;压轴题.
【答案】见试题解答内容
【分析】(1)直接找一组勾股数代入方程即可;
(2)通过判断根的判别式△的正负来证明结论;
(3)利用根的意义和勾股定理作为相等关系先求得c的值,根据完全平方公式求得ab的值,从而可求得面积.
【解答】(1)解:当a=3,b=4,c=5时
勾系一元二次方程为3x2+5x+4=0;
(2)证明:根据题意,得
Δ=(c)2﹣4ab=2c2﹣4ab
∵a2+b2=c2
∴2c2﹣4ab=2(a2+b2)﹣4ab=2(a﹣b)2≥0
即△≥0
∴勾系一元二次方程必有实数根;
(3)解:当x=﹣1时,有ac+b=0,即a+bc
∵2a+2bc=6,即2(a+b)c=6
∴3c=6
∴c=2
∴a2+b2=c2=4,a+b=2
∵(a+b)2=a2+b2+2ab
∴ab=2
∴S△ABCab=1.
【点评】此类题目要读懂题意,根据题目中所给的材料结合勾股定理和根的判别式解题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
中考数学一轮复习 一元二次方程
一.选择题(共10小题)
1.(2025春 蜀山区校级期中)关于x的一元二次方程(a﹣1)x2+x+a2﹣1=0的一个根是0,则a的值为( )
A.1 B.﹣1 C.1或﹣1 D.
2.(2025 枣庄)若关于x的一元二次方程x2﹣2x+kb+1=0有两个不相等的实数根,则一次函数y=kx+b的大致图象可能是( )
A. B.
C. D.
3.(2025 桂林)若关于x的一元二次方程(k﹣1)x2+4x+1=0有两个不相等的实数根,则k的取值范围是( )
A.k<5 B.k<5,且k≠1 C.k≤5,且k≠1 D.k>5
4.(2025 安顺)一个等腰三角形的两条边长分别是方程x2﹣7x+10=0的两根,则该等腰三角形的周长是( )
A.12 B.9 C.13 D.12或9
5.(2025 江北区期末)对于一元二次方程ax2+bx+c=0(a≠0),下列说法:
①若a+b+c=0,则b2﹣4ac≥0;
②若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
③若c是方程ax2+bx+c=0的一个根,则一定有ac+b+1=0成立;
④若x0是一元二次方程ax2+bx+c=0的根,则
⑤存在实数m、n(m≠n),使得am2+bm+c=an2+bn+c;
其中正确的( )
A.只有①②④ B.只有①②④⑤ C.①②③④⑤ D.只有①②③
6.(2025 武进区校级自主招生)设关于x的方程ax2+(a+2)x+9a=0,有两个不相等的实数根x1、x2,且x1<1<x2,那么实数a的取值范围是( )
A. B. C. D.
7.(2025 呼伦贝尔)某种品牌运动服经过两次降价,每件零售价由560元降为315元,已知两次降价的百分率相同,求每次降价的百分率.设每次降价的百分率为x,下面所列的方程中正确的是( )
A.560(1+x)2=315 B.560(1﹣x)2=315
C.560(1﹣2x)2=315 D.560(1﹣x2)=315
8.(2025 深圳模拟)已知α、β是方程x2﹣2x﹣4=0的两个实数根,则α3+8β+6的值为( )
A.﹣1 B.2 C.22 D.30
9.(2024秋 贵州期末)把方程x(x+2)=5(x﹣2)化成一般式,则a、b、c的值分别是( )
A.1,﹣3,10 B.1,7,﹣10 C.1,﹣5,12 D.1,3,2
10.(2025 广州)已知2是关于x的方程x2﹣2mx+3m=0的一个根,并且这个方程的两个根恰好是等腰三角形ABC的两条边长,则三角形ABC的周长为( )
A.10 B.14 C.10或14 D.8或10
二.填空题(共5小题)
11.(2025 海曙区自主招生)如果方程(x﹣1)(x2﹣2x)=0的三根可以作为一个三角形的三边之长,那么实数k的取值范围是 .
12.(2025 沂源县一模)如果恰好只有一个实数a是方程(k2﹣9)x2﹣2(k+1)x+1=0的根,则k的值为 .
13.(2025 临沂)对于实数a,b,定义运算“*”:a*b.例如4*2,因为4>2,所以4*2=42﹣4×2=8.若x1,x2是一元二次方程x2﹣5x+6=0的两个根,则x1*x2= .
14.(2025 温江区校级自主招生)若关于x的方程(1﹣m2)x2+2mx﹣1=0的所有根都是比1小的正实数,则实数m的取值范围是 .
15.(2025 贵阳)如图,在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高.动点P从点A出发,沿A→D方向以cm/s的速度向点D运动.设△ABP的面积为S1,矩形PDFE的面积为S2,运动时间为t秒(0<t<8),则t= 秒时,S1=2S2.
三.解答题(共5小题)
16.(2025 湖北)如图,一农户要建一个矩形猪舍,猪舍的一边利用长为12m的住房墙,另外三边用25m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,所围矩形猪舍的长、宽分别为多少时,猪舍面积为80m2?
17.(2025 淮安)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
18.(2024秋 定安县校级月考)如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2cm/s的速度向D移动.
(1)P、Q两点从出发开始到几秒时,四边形PBCQ的面积为33cm2;
(2)P、Q两点从出发开始到几秒时,点P和点Q的距离是10cm.
19.(2025 北京)关于x的一元二次方程x2﹣(k+3)x+2k+2=0.
(1)求证:方程总有两个实数根;
(2)若方程有一个根小于1,求k的取值范围.
20.(2025 濉溪县三模)如图,四边形ACDE是证明勾股定理时用到的一个图形,a,b,c是Rt△ABC和Rt△BED边长,易知,这时我们把关于x的形如的一元二次方程称为“勾系一元二次方程”.
请解决下列问题:
(1)写出一个“勾系一元二次方程”;
(2)求证:关于x的“勾系一元二次方程”必有实数根;
(3)若x=﹣1是“勾系一元二次方程”的一个根,且四边形ACDE的周长是6,求△ABC面积.
中考数学一轮复习 一元二次方程
参考答案与试题解析
一.选择题(共10小题)
1.(2025春 蜀山区校级期中)关于x的一元二次方程(a﹣1)x2+x+a2﹣1=0的一个根是0,则a的值为( )
A.1 B.﹣1 C.1或﹣1 D.
【考点】一元二次方程的解.
【专题】符号意识;应用意识.
【答案】B
【分析】根据方程的解的定义,把x=0代入方程,即可得到关于a的方程,再根据一元二次方程的定义即可求解.
【解答】解:根据题意得:a2﹣1=0且a﹣1≠0,
解得:a=﹣1.
故选:B.
【点评】本题主要考查了一元二次方程的解的定义,特别需要注意的条件是二次项系数不等于0.
2.(2025 枣庄)若关于x的一元二次方程x2﹣2x+kb+1=0有两个不相等的实数根,则一次函数y=kx+b的大致图象可能是( )
A. B.
C. D.
【考点】根的判别式;一次函数的图象.
【答案】B
【分析】根据一元二次方程x2﹣2x+kb+1=0有两个不相等的实数根,得到判别式大于0,求出kb的符号,对各个图象进行判断即可.
【解答】解:∵x2﹣2x+kb+1=0有两个不相等的实数根,
∴Δ=4﹣4(kb+1)>0,
解得kb<0,
A.k>0,b>0,即kb>0,故A不正确;
B.k>0,b<0,即kb<0,故B正确;
C.k<0,b<0,即kb>0,故C不正确;
D.k<0,b=0,即kb=0,故D不正确;
故选:B.
【点评】本题考查的是一元二次方程根的判别式和一次函数的图象,一元二次方程根的情况与判别式△的关系:(1)Δ>0 方程有两个不相等的实数根;(2)Δ=0 方程有两个相等的实数根;(3)Δ<0 方程没有实数根.
3.(2025 桂林)若关于x的一元二次方程(k﹣1)x2+4x+1=0有两个不相等的实数根,则k的取值范围是( )
A.k<5 B.k<5,且k≠1 C.k≤5,且k≠1 D.k>5
【考点】根的判别式;一元二次方程的定义.
【答案】B
【分析】根据方程为一元二次方程且有两个不相等的实数根,结合一元二次方程的定义以及根的判别式即可得出关于k的一元一次不等式组,解不等式组即可得出结论.
【解答】解:∵关于x的一元二次方程(k﹣1)x2+4x+1=0有两个不相等的实数根,
∴,即,
解得:k<5且k≠1.
故选:B.
【点评】本题考查了根的判别式以及一元二次方程的定义,解题的关键是得出关于k的一元一次不等式组.本题属于基础题,难度不大,解决该题型题目时,根据方程根的个数结合一元二次方程的定义以及根的判别式得出不等式组是关键.
4.(2025 安顺)一个等腰三角形的两条边长分别是方程x2﹣7x+10=0的两根,则该等腰三角形的周长是( )
A.12 B.9 C.13 D.12或9
【考点】解一元二次方程﹣因式分解法;三角形三边关系;等腰三角形的性质.
【答案】A
【分析】求出方程的解,即可得出三角形的边长,再求出即可.
【解答】解:x2﹣7x+10=0,
(x﹣2)(x﹣5)=0,
x﹣2=0,x﹣5=0,
x1=2,x2=5,
①等腰三角形的三边是2,2,5
∵2+2<5,
∴不符合三角形三边关系定理,此时不符合题意;
②等腰三角形的三边是2,5,5,此时符合三角形三边关系定理,三角形的周长是2+5+5=12;
即等腰三角形的周长是12.
故选:A.
【点评】本题考查了等腰三角形性质、解一元二次方程、三角形三边关系定理的应用等知识,关键是求出三角形的三边长.
5.(2025 江北区期末)对于一元二次方程ax2+bx+c=0(a≠0),下列说法:
①若a+b+c=0,则b2﹣4ac≥0;
②若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
③若c是方程ax2+bx+c=0的一个根,则一定有ac+b+1=0成立;
④若x0是一元二次方程ax2+bx+c=0的根,则
⑤存在实数m、n(m≠n),使得am2+bm+c=an2+bn+c;
其中正确的( )
A.只有①②④ B.只有①②④⑤ C.①②③④⑤ D.只有①②③
【考点】根的判别式.
【专题】压轴题;判别式法;一元二次方程及应用;运算能力;推理能力.
【答案】B
【分析】按照方程的解的含义、一元二次方程的实数根与判别式的关系、等式的性质、一元二次方程的求根公式等对各选项分别讨论,可得答案.
【解答】解:①若a+b+c=0,则x=1是方程ax2+bx+c=0的解,
由一元二次方程的实数根与判别式的关系可知Δ=b2﹣4ac≥0,故①正确;
②∵方程ax2+c=0有两个不相等的实根,
∴Δ=0﹣4ac>0,
∴﹣4ac>0,
则方程ax2+bx+c=0的判别式Δ=b2﹣4ac>0,
∴方程ax2+bx+c=0必有两个不相等的实根,故②正确;
③∵c是方程ax2+bx+c=0的一个根,
则ac2+bc+c=0,
∴c(ac+b+1)=0,
若c=0,等式仍然成立,
但ac+b+1=0不一定成立,故③不正确;
④若x0是一元二次方程ax2+bx+c=0的根,
则由求根公式可得:
x0或x0
∴2ax0+b或2ax0+b
∴
故④正确.
⑤存在实数m、n(m≠n),使得am2+bm+c=an2+bn+c成立;
∵由am2+bm+c=an2+bn+c,
∴a(m2﹣n2)+b(m﹣n)=0,
∴a(m﹣n)(m+n)+b(m﹣n)=0,
即(m﹣n)[a(m+n)+b]=0,
∵m≠n,
∴a(m+n)+b=0,
∴当a≠0时,存在实数m、n(m≠n),使得am2+bm+c=an2+bn+c成立;
故⑤正确.
故选:B.
【点评】本题主要考查了一元二次方程的实数根与判别式的关系,牢固掌握二者的关系并灵活运用,是解题的关键.
6.(2025 武进区校级自主招生)设关于x的方程ax2+(a+2)x+9a=0,有两个不相等的实数根x1、x2,且x1<1<x2,那么实数a的取值范围是( )
A. B. C. D.
【考点】根与系数的关系;根的判别式.
【专题】转化思想.
【答案】D
【分析】方法1、根据一元二次方程的根的判别式,建立关于a的不等式,求出a的取值范围.又存在x1<1<x2,即(x1﹣1)(x2﹣1)<0,x1x2﹣(x1+x2)+1<0,利用根与系数的关系,从而最后确定a的取值范围.
方法2、由方程有两个实数根即可得出此方程是一元二次方程,而x1<1<x2,可以看成是二次函数y=ax2+(a+2)x+9a的图象与x轴的两个交点在1左右两侧,由此得出自变量x=1时,对应的函数值的符号,即可得出结论.
【解答】解:方法1、∵方程有两个不相等的实数根,
则a≠0且Δ>0,
由(a+2)2﹣4a×9a=﹣35a2+4a+4>0,
解得a,
∵x1+x2,x1x2=9,
又∵x1<1<x2,
∴x1﹣1<0,x2﹣1>0,
那么(x1﹣1)(x2﹣1)<0,
∴x1x2﹣(x1+x2)+1<0,
即91<0,
解得a<0,
最后a的取值范围为:a<0.
故选D.
方法2、由题意知,a≠0,令y=ax2+(a+2)x+9a,
由于方程的两根一个大于1,一个小于1,
∴抛物线与x轴的交点分别在1两侧,
当a>0时,x=1时,y<0,
∴a+(a+2)+9a<0,
∴a(不符合题意,舍去),
当a<0时,x=1时,y>0,
∴a+(a+2)+9a>0,
∴a,
∴a<0,
故选:D.
【点评】总结:1、一元二次方程根的情况与判别式△的关系:
(1)Δ>0 方程有两个不相等的实数根;
(2)Δ=0 方程有两个相等的实数根;
(3)Δ<0 方程没有实数根.
2、根与系数的关系为:x1+x2,x1x2.
7.(2025 呼伦贝尔)某种品牌运动服经过两次降价,每件零售价由560元降为315元,已知两次降价的百分率相同,求每次降价的百分率.设每次降价的百分率为x,下面所列的方程中正确的是( )
A.560(1+x)2=315 B.560(1﹣x)2=315
C.560(1﹣2x)2=315 D.560(1﹣x2)=315
【考点】由实际问题抽象出一元二次方程.
【专题】增长率问题.
【答案】B
【分析】设每次降价的百分率为x,根据降价后的价格=降价前的价格(1﹣降价的百分率),则第一次降价后的价格是560(1﹣x),第二次降价后的价格是560(1﹣x)2,据此即可列方程求解.
【解答】解:设每次降价的百分率为x,由题意得:
560(1﹣x)2=315,
故选:B.
【点评】此题主要考查了由实际问题抽象出一元二次方程,关键是根据题意找到等式两边的平衡条件,这种价格问题主要解决价格变化前后的平衡关系,列出方程即可.
8.(2025 深圳模拟)已知α、β是方程x2﹣2x﹣4=0的两个实数根,则α3+8β+6的值为( )
A.﹣1 B.2 C.22 D.30
【考点】一元二次方程的解.
【专题】计算题.
【答案】D
【分析】根据根与系数的关系得到α+β=2,由一元二次方程解的定义得到α2﹣2α﹣4=0,则α2=2α+4,然后将其代入所求的代数式,并求值.
【解答】解:∵α、β是方程x2﹣2x﹣4=0的两个实数根,
∴α+β=2,α2﹣2α﹣4=0,
∴α2=2α+4
∴α3+8β+6=α α2+8β+6
=α (2α+4)+8β+6
=2α2+4α+8β+6
=2(2α+4)+4α+8β+6
=8α+8β+14
=8(α+β)+14=30,
故选:D.
【点评】本题主要考查了一元二次方程的解.解答本题时,利用根与系数得到α+β=2,α2﹣2α﹣4=0是解题的关键.
9.(2024秋 贵州期末)把方程x(x+2)=5(x﹣2)化成一般式,则a、b、c的值分别是( )
A.1,﹣3,10 B.1,7,﹣10 C.1,﹣5,12 D.1,3,2
【考点】一元二次方程的一般形式.
【专题】推理填空题;一元二次方程及应用.
【答案】A
【分析】a、b、c分别指的是一元二次方程的一般式中的二次项系数、一次项系数、常数项.
【解答】解:由方程x(x+2)=5(x﹣2),得
x2﹣3x+10=0,
∴a、b、c的值分别是1、﹣3、10;
故选:A.
【点评】本题考查了一元二次方程的一般形式.一元二次方程的一般形式是:ax2+bx+c=0(a,b,c是常数且a≠0),在一般形式中ax2叫二次项,bx叫一次项,c是常数项.其中a,b,c分别叫二次项系数,一次项系数,常数项.
10.(2025 广州)已知2是关于x的方程x2﹣2mx+3m=0的一个根,并且这个方程的两个根恰好是等腰三角形ABC的两条边长,则三角形ABC的周长为( )
A.10 B.14 C.10或14 D.8或10
【考点】解一元二次方程﹣因式分解法;三角形三边关系;等腰三角形的性质;一元二次方程的解.
【答案】B
【分析】先将x=2代入x2﹣2mx+3m=0,求出m=4,则方程即为x2﹣8x+12=0,利用因式分解法求出方程的根x1=2,x2=6,分两种情况:①当6是腰时,2是底边;②当6是底边时,2是腰进行讨论.注意两种情况都要用三角形三边关系定理进行检验.
【解答】解:∵2是关于x的方程x2﹣2mx+3m=0的一个根,
∴22﹣4m+3m=0,m=4,
∴x2﹣8x+12=0,
解得x1=2,x2=6.
①当6是腰时,2是底边,此时周长=6+6+2=14;
②当6是底边时,2是腰,2+2<6,不能构成三角形.
所以它的周长是14.
故选:B.
【点评】此题主要考查了一元二次方程的解,解一元二次方程﹣因式分解法,三角形三边关系定理以及等腰三角形的性质,注意求出三角形的三边后,要用三边关系定理检验.
二.填空题(共5小题)
11.(2025 海曙区自主招生)如果方程(x﹣1)(x2﹣2x)=0的三根可以作为一个三角形的三边之长,那么实数k的取值范围是 3<k≤4 .
【考点】根与系数的关系;三角形三边关系;根的判别式.
【专题】压轴题.
【答案】见试题解答内容
【分析】根据原方程可得出:①x﹣1=0,②x2﹣2x0;根据根与系数的关系,可求出②方程的x1+x2和x1﹣x2的表达式,然后根据三角形三边关系定理求出k的取值范围.
【解答】解:由题意,得:x﹣1=0,x2﹣2x0;
设x2﹣2x0的两根分别是m、n(m≥n);则m+n=2,mn;
m﹣n;
根据三角形三边关系定理,得:
m﹣n<1<m+n,即1<2;
∴,解得3<k≤4.
【点评】此题主要考查的是一元二次方程根与系数的关系以及三角形三边关系定理.
12.(2025 沂源县一模)如果恰好只有一个实数a是方程(k2﹣9)x2﹣2(k+1)x+1=0的根,则k的值为 ±3或﹣5 .
【考点】根的判别式.
【专题】计算题.
【答案】见试题解答内容
【分析】分原方程是一元一次方程和一元二次方程两种情况讨论即可得到答案.
【解答】解:①当原方程是一个一元一次方程时,方程只有一个实数根,
则k2﹣9=0,
解得k=±3,
②如果方程是一元二次方程时,则方程有两个相等的实数根,
即Δ=b2﹣4ac=0,
即:4(k+1)2﹣4(k2﹣9)=0
解得:k=﹣5.
故答案为±3或﹣5.
【点评】本题考查了根的判别式,同时还考查了分类讨论思想,是一道好题.
13.(2025 临沂)对于实数a,b,定义运算“*”:a*b.例如4*2,因为4>2,所以4*2=42﹣4×2=8.若x1,x2是一元二次方程x2﹣5x+6=0的两个根,则x1*x2= 3或﹣3 .
【考点】解一元二次方程﹣因式分解法.
【专题】压轴题;新定义.
【答案】见试题解答内容
【分析】首先解方程x2﹣5x+6=0,再根据a*b,求出x1*x2的值即可.
【解答】解:∵x1,x2是一元二次方程x2﹣5x+6=0的两个根,
∴(x﹣3)(x﹣2)=0,
解得:x=3或2,
①当x1=3,x2=2时,x1*x2=32﹣3×2=3;
②当x1=2,x2=3时,x1*x2=3×2﹣32=﹣3.
故答案为:3或﹣3.
【点评】此题主要考查了因式分解法解一元二次方程以及利用材料分析解决新问题,根据已知进行分类讨论是解题关键.
14.(2025 温江区校级自主招生)若关于x的方程(1﹣m2)x2+2mx﹣1=0的所有根都是比1小的正实数,则实数m的取值范围是 m=1或m>2 .
【考点】根与系数的关系.
【专题】分类讨论.
【答案】见试题解答内容
【分析】分1﹣m2=0,1﹣m2≠0两种情况先求出原方程的实数根,再根据两个实数根都是比1小的正实数,列出不等式,求出m的取值范围.
【解答】解:当1﹣m2=0时,m=±1.
当m=1时,可得2x﹣1=0,x,符合题意;
当m=﹣1时,可得﹣2x﹣1=0,x,不符合题意;
当1﹣m2≠0时,(1﹣m2)x2+2mx﹣1=0,
[(1+m)x﹣1][(1﹣m)x+1]=0,
∴x1,x2.
∵关于x的方程(1﹣m2)x2+2mx﹣1=0的所有根都是比1小的正实数,
∴01,解得m>0,
01,解得m>2.
综上可得,实数m的取值范围是m=1或m>2.
故答案为:m=1或m>2.
【点评】考查了解一元二次方程及解一元一次不等式,解题的关键是将二次项系数分1﹣m2=0,1﹣m2≠0两种情况讨论求解.
15.(2025 贵阳)如图,在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高.动点P从点A出发,沿A→D方向以cm/s的速度向点D运动.设△ABP的面积为S1,矩形PDFE的面积为S2,运动时间为t秒(0<t<8),则t= 6 秒时,S1=2S2.
【考点】一元二次方程的应用;等腰直角三角形;矩形的性质.
【专题】几何动点问题;压轴题.
【答案】见试题解答内容
【分析】利用三角形的面积公式以及矩形的面积公式,表示出S1和S2,然后根据S1=2S2,即可列方程求解.
【解答】解:∵Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高,
∴AD=BD=CD=8cm,
又∵APt,
则S1AP BD8t=8t,PD=8t,
∵PE∥BC,
∴△APE∽△ADC,
∴,
∴PE=APt,
∴S2=PD PE=(8t) t,
∵S1=2S2,
∴8t=2(8t) t,
解得:t=6.
故答案为:6.
【点评】本题考查了一元二次方程的应用,以及等腰直角三角形的性质,正确表示出S1和S2是关键.
三.解答题(共5小题)
16.(2025 湖北)如图,一农户要建一个矩形猪舍,猪舍的一边利用长为12m的住房墙,另外三边用25m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,所围矩形猪舍的长、宽分别为多少时,猪舍面积为80m2?
【考点】一元二次方程的应用.
【专题】几何图形问题.
【答案】见试题解答内容
【分析】设矩形猪舍垂直于住房墙一边长为x m可以得出平行于墙的一边的长为(25﹣2x+1)m.根据矩形的面积公式建立方程求出其解就可以了.
【解答】解:设矩形猪舍垂直于住房墙一边长为x m可以得出平行于墙的一边的长为(25﹣2x+1)m,由题意得
x(25﹣2x+1)=80,
化简,得x2﹣13x+40=0,
解得:x1=5,x2=8,
当x=5时,26﹣2x=16>12(舍去),当x=8时,26﹣2x=10<12,
答:所围矩形猪舍的长为10m、宽为8m.
【点评】本题考查了列一元二次方程解实际问题的运用,矩形的面积公式的运用及一元二次方程的解法的运用,解答时寻找题目的等量关系是关键.
17.(2025 淮安)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 (100+200x) 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
【考点】一元二次方程的应用.
【专题】销售问题.
【答案】见试题解答内容
【分析】(1)销售量=原来销售量+下降销售量,据此列式即可;
(2)根据销售量×每斤利润=总利润列出方程求解即可.
【解答】解:(1)将这种水果每斤的售价降低x元,则每天的销售量是10020=(100+200x)(斤);
(2)根据题意得:(4﹣2﹣x)(100+200x)=300,
解得:x或x=1,
当x时,销售量是100+200200<260;
当x=1时,销售量是100+200=300(斤).
∵每天至少售出260斤,
∴x=1.
答:张阿姨需将每斤的售价降低1元.
【点评】本题考查理解题意的能力,第一问关键求出每千克的利润,求出总销售量,从而利润.第二问,根据售价和销售量的关系,以利润作为等量关系列方程求解.
18.(2024秋 定安县校级月考)如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2cm/s的速度向D移动.
(1)P、Q两点从出发开始到几秒时,四边形PBCQ的面积为33cm2;
(2)P、Q两点从出发开始到几秒时,点P和点Q的距离是10cm.
【考点】一元二次方程的应用.
【专题】几何动点问题;压轴题.
【答案】见试题解答内容
【分析】(1)设P、Q两点从出发开始到x秒时四边形PBCQ的面积为33cm2,则PB=(16﹣3x)cm,QC=2xcm,根据梯形的面积公式可列方程:(16﹣3x+2x)×6=33,解方程可得解;
(2)作QE⊥AB,垂足为E,设运动时间为t秒,用t表示线段长,用勾股定理列方程求解.
【解答】解:(1)设P、Q两点从出发开始到x秒时四边形PBCQ的面积为33cm2,
则PB=(16﹣3x)cm,QC=2xcm,
根据梯形的面积公式得(16﹣3x+2x)×6=33,
解之得x=5,
(2)设P,Q两点从出发经过t秒时,点P,Q间的距离是10cm,
作QE⊥AB,垂足为E,
则QE=AD=6,PQ=10,
∵PA=3t,CQ=BE=2t,
∴PE=AB﹣AP﹣BE=|16﹣5t|,
由勾股定理,得(16﹣5t)2+62=102,
解得t1=4.8,t2=1.6.
答:(1)P、Q两点从出发开始到5秒时四边形PBCQ的面积为33cm2;
(2)从出发到1.6秒或4.8秒时,点P和点Q的距离是10cm.
【点评】(1)主要用到了梯形的面积公式:S(上底+下底)×高;(2)作辅助线是关键,构成直角三角形后,用了勾股定理.
19.(2025 北京)关于x的一元二次方程x2﹣(k+3)x+2k+2=0.
(1)求证:方程总有两个实数根;
(2)若方程有一个根小于1,求k的取值范围.
【考点】根的判别式.
【答案】见试题解答内容
【分析】(1)根据方程的系数结合根的判别式,可得Δ=(k﹣1)2≥0,由此可证出方程总有两个实数根;
(2)利用分解因式法解一元二次方程,可得出x1=2、x2=k+1,根据方程有一根小于1,即可得出关于k的一元一次不等式,解之即可得出k的取值范围.
【解答】(1)证明:∵在方程x2﹣(k+3)x+2k+2=0中,Δ=[﹣(k+3)]2﹣4×1×(2k+2)=k2﹣2k+1=(k﹣1)2≥0,
∴方程总有两个实数根.
(2)解:∵x2﹣(k+3)x+2k+2=(x﹣2)(x﹣k﹣1)=0,
∴x1=2,x2=k+1.
∵方程有一根小于1,
∴k+1<1,解得:k<0,
∴k的取值范围为k<0.
【点评】本题考查了根的判别式、因式分解法解一元二次方程以及解一元一次不等式,解题的关键是:(1)牢记“当△≥0时,方程有两个实数根”;(2)利用因式分解法解一元二次方程结合方程一根小于1,找出关于k的一元一次不等式.
20.(2025 濉溪县三模)如图,四边形ACDE是证明勾股定理时用到的一个图形,a,b,c是Rt△ABC和Rt△BED边长,易知,这时我们把关于x的形如的一元二次方程称为“勾系一元二次方程”.
请解决下列问题:
(1)写出一个“勾系一元二次方程”;
(2)求证:关于x的“勾系一元二次方程”必有实数根;
(3)若x=﹣1是“勾系一元二次方程”的一个根,且四边形ACDE的周长是6,求△ABC面积.
【考点】一元二次方程的应用;勾股定理的证明.
【专题】几何图形问题;压轴题.
【答案】见试题解答内容
【分析】(1)直接找一组勾股数代入方程即可;
(2)通过判断根的判别式△的正负来证明结论;
(3)利用根的意义和勾股定理作为相等关系先求得c的值,根据完全平方公式求得ab的值,从而可求得面积.
【解答】(1)解:当a=3,b=4,c=5时
勾系一元二次方程为3x2+5x+4=0;
(2)证明:根据题意,得
Δ=(c)2﹣4ab=2c2﹣4ab
∵a2+b2=c2
∴2c2﹣4ab=2(a2+b2)﹣4ab=2(a﹣b)2≥0
即△≥0
∴勾系一元二次方程必有实数根;
(3)解:当x=﹣1时,有ac+b=0,即a+bc
∵2a+2bc=6,即2(a+b)c=6
∴3c=6
∴c=2
∴a2+b2=c2=4,a+b=2
∵(a+b)2=a2+b2+2ab
∴ab=2
∴S△ABCab=1.
【点评】此类题目要读懂题意,根据题目中所给的材料结合勾股定理和根的判别式解题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
