(小升初开学分班考)小升初开学名校分班摸底押题卷-2025年秋六年级数学北师大版(含答案解析)
文档属性
| 名称 | (小升初开学分班考)小升初开学名校分班摸底押题卷-2025年秋六年级数学北师大版(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 137.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-16 00:30:38 | ||
图片预览




文档简介
/ 让学习更有效 小升初备考 | 数学学科
2025年秋六年级数学小升初开学名校分班摸底押题卷(北师大版)
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题
1.如图中圆锥的体积与圆柱( )的体积相等.
A. B. C. D.
2.某班男生的平均身高是165厘米。请你判断,下面哪位男生最不可能是这个班的?( )
A.齐齐身高168厘米,是篮球队中锋 B.力力身高132厘米,是全班最矮的
C.青青身高165厘米,是全班最高的。 D.睿睿身高180厘米
3.用一副三角板可以画出的角是( )
A.160° B.40° C.105° D.125°
4.下面能折成正方体的是( )
A. B. C. D.
5.从侧面看是的组合体是( )
A. B. C. D.
6.下列选项中,正确的是( )
A.圆的半径和周长成正比例 B.3100÷300=31÷3=0……1
C.所有的质数都是合数 D.长方体是特殊的正方体
7.观察如图的正方体展开图,与⑤号面相对的是( )号面。
A.① B.② C.③ D.⑥
8.下面说法正确的是( )
A.圆锥的侧面展开图是一个等腰三角形
B.小华身高1.2米,她在平均水深是1米的水池中游泳是绝对安全的
C.圆的面积和半径成正比例
D.如果ab=cd(a、b、c、d均不为0),那么a:c=d:b
9.规定10t记作0t,11t记作+1t,则下列说法错误的是( )
A.8t记作﹣8t B.15t记作+5t C.6t记作﹣4t D.+3t表示13t
10.13.6%去掉百分号后,这个数就( )
A.扩大为原来的100倍 B.缩小为原来的
C.大小不变 D.无法确定
11.妙想做抛硬币的游戏(硬币是均匀的)。下列说法正确的是( )
A.妙想抛20次硬币,一定是10次正面朝上,10次反面朝上
B.妙想前4次抛的结果都是反面朝上,第5次一定会正面朝上
C.妙想做了1000次抛硬币的游戏,正面朝上的次数和反面朝上的次数的比值接近或等于1
D.妙想抛了10次硬币,不可能8次正面朝上
12.已知三角形一个角是30°,另外两个内角的度数比是1:4,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.等腰直角三角形 D.钝角三角形
二.填空题
13.深圳,简称“深”,别称“鹏城”,是国务院批复确定的中国经济特区、全国性经济中心城市和国际化城市。根据第七次全国人口普查结果,深圳市常住人口为17560061人,这个数读作 ,把这个数省略万位后面的尾数约是 万。
14.(1)5吨60千克= 吨;(2)3.15时= 时 分。
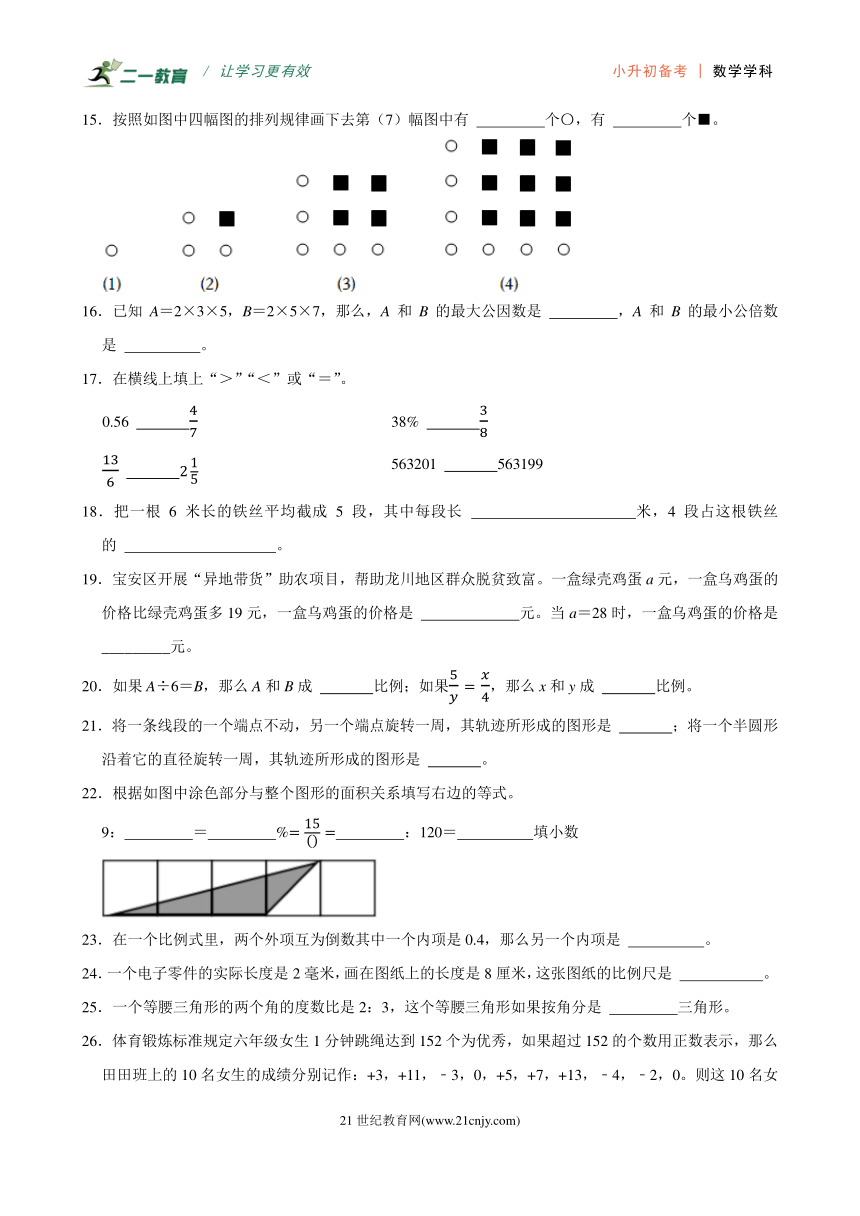
15.按照如图中四幅图的排列规律画下去第(7)幅图中有 个〇,有 个■。
16.已知A=2×3×5,B=2×5×7,那么,A和B的最大公因数是 ,A和B的最小公倍数是 。
17.在横线上填上“>”“<”或“=”。
0.56 38%
563201 563199
18.把一根6米长的铁丝平均截成5段,其中每段长 米,4段占这根铁丝的 。
19.宝安区开展“异地带货”助农项目,帮助龙川地区群众脱贫致富。一盒绿壳鸡蛋a元,一盒乌鸡蛋的价格比绿壳鸡蛋多19元,一盒乌鸡蛋的价格是 元。当a=28时,一盒乌鸡蛋的价格是_________元。
20.如果A÷6=B,那么A和B成 比例;如果,那么x和y成 比例。
21.将一条线段的一个端点不动,另一个端点旋转一周,其轨迹所形成的图形是 ;将一个半圆形沿着它的直径旋转一周,其轨迹所形成的图形是 。
22.根据如图中涂色部分与整个图形的面积关系填写右边的等式。
9: = % :120= 填小数
23.在一个比例式里,两个外项互为倒数其中一个内项是0.4,那么另一个内项是 。
24.一个电子零件的实际长度是2毫米,画在图纸上的长度是8厘米,这张图纸的比例尺是 。
25.一个等腰三角形的两个角的度数比是2:3,这个等腰三角形如果按角分是 三角形。
26.体育锻炼标准规定六年级女生1分钟跳绳达到152个为优秀,如果超过152的个数用正数表示,那么田田班上的10名女生的成绩分别记作:+3,+11,﹣3,0,+5,+7,+13,﹣4,﹣2,0。则这10名女生1分钟跳绳的平均成绩是 个,这10名女生1分钟跳绳的优秀率是 %
三.计算题
27.直接写出得数。
5.07﹣2.8= 34÷4= 1
28.解方程。
2.3:6=x: 3x÷5=20 0.8x+1.6x=48
29.用你喜欢的方法计算下面各题。
728﹣28×4 17÷[2﹣()] 33.5×0.58+6.65×5.8
四.操作题
30.(1)如图,方格中标出了A、B、C、D四个点,如果用数对表示这4个点的位置,A为(4,4)、C为(7,2)。那么B、D点的位置用数对表示分别是:B( , )、D( , )。
(2)如果将D点向 (填“左”或“右”)平移2格后,再顺次连接4个点可以围成一个平行四边形。画出这个平行四边形,我们把这个平行四边形叫做图形①。
(3)以直线a为对称轴,画出这个平行四边形的轴对称图形,得到图形②。
(4)画出图形②按1:2缩小后的图形,得到图形③。
五.应用题
31.爸爸打算给书房铺上方砖,用边长3分米的方砖需要120块,如果改用面积为36平方分米的方砖,需要多少块?
32.神舟十三号女性舱外航天服重约90千克,男性舱外航天服重约120千克,女性舱外航天服比男性舱外航天服轻百分之几?(先画示意图,再列式解答)
33.一个底面半径是6厘米的圆柱形玻璃器皿里装有一些水,水中浸没着一个高9厘米的圆锥体铅锤。当铅锤从水中取出后,水面下降了0.5厘米。这个圆锥体的底面积是多少平方厘米?
34.一个直角三角形的两条直角边分别长6厘米和8厘米,斜边的长度是10厘米,小智以8厘米长的直角边为轴旋转这个三角形,得到一个圆锥体,这个圆锥体的体积是多少立方厘米?
35.一条铁路长72米,甲乙两个工程队同时从两端开始维修,乙队每天维修的长度是甲队的,4天后修完。甲乙两队每天各修了多少米?
36.足球社团购买了一批足球,已知一个足球是由32块黑色正五边形和白色正六边形的皮块制成的,黑、白皮块的块数比是3:5,那么黑色和白色皮分别有多少块?
参考答案及试题解析
一.选择题
1.【考点】圆锥的体积;圆柱的侧面积、表面积和体积.
【答案】C
【思路分析】因为等底等高的圆柱的体积是圆锥体积的3倍,所以当圆柱与圆锥的体积相等、底面积相等时,圆柱的高是圆锥高的,据此解答.
【解答】解:124
所以,底面直径是6,高是12的圆锥与底面直径是6,高是4的圆柱的体积相等.
故选:C.
【名师点评】此题考查的目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及应用.
2.【考点】平均数的含义及求平均数的方法.
【答案】C
【思路分析】根据平均数是反应一组数据的集中趋势的量,它比最大数小,比最小数大,据此解答即可。
【解答】解:某班男生的平均身高是165厘米,青青身高165厘米,是全班最高的,所以青青最不可能是这个班的。
故选:C。
【名师点评】根据平均数的含义和求法,解答即可。
3.【考点】图形的拼组.
【答案】C
【思路分析】先明确一副三角板的六个角共有四个度数,30°,45°,60°,90°,然后进行加减运算,找到符合条件的角。
【解答】解:利用一副三角板可以画出的角有:30°,45°,60°,90°;30°+45°=75°,30°+90°=120°,45°+60°=105°,45°+90°=135°,60°+90°=150°,30°+45°+90°=165°;45°﹣30°=15°,一共可以画出11个角。因此105°的角可以利用三角板画出。
故选:C。
【名师点评】此题结合生活实际,既考查了对角和三角板的认识,又考查了同学们的完全归纳能力。
4.【考点】正方体的展开图.
【答案】C
【思路分析】根据正方体展开图的特征可知,图C符合正方体展开图的“2﹣2﹣2”结构,所以图C能折成正方体。据此解答即可。
【解答】解:符合正方体展开图的“2﹣2﹣2”结构,所以图C能折成正方体。
故选:C。
【名师点评】此题考查的目的是理解掌握正方体展开图的特征,训练学生的观察能力和空间想象能力。
5.【考点】从不同方向观察物体和几何体.
【答案】B
【思路分析】根据观察选项,侧面图形依次为,,,。
【解答】解:从侧面看是的组合体是。
故选:B。
【名师点评】本题是考查从不同方向观察物体和几何图形,关键是培养学生的观察能力。
6.【考点】辨识成正比例的量与成反比例的量;合数与质数的初步认识.
【答案】A
【思路分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例;被除数和除数都乘或除以一个相同的数(0除外),商不变,余数也同时乘或除以一个相同的数(0除外);根据质数、合数的意义判断;正方体是特殊的长方体。
【解答】解:A.圆的周长÷圆的半径=2π(一定),商一定,所以圆的半径和周长成正比例,正确;
B.3100÷300=31÷3,3100÷300=10……100,所以原题计算错误;
C.一个数只有1和它本身两个因数的数叫质数,除了1和它本身还有其它因数的数叫合数,所有的质数都不是合数,所以原题说法错误;
D.当长方体的长、宽、高相等时,就是正方体,正方体是特殊的长方体,所以原题说法错误;
故选:A。
【名师点评】本题考查了判断两个相关联的量之间成什么比例的方法、商的变化规律、质数、合数的意义以及长方体与正方体的关系。
7.【考点】正方体的展开图.
【答案】B
【思路分析】正方体的平面展开图中,相对面的特点是中间必须间隔一个正方形,据此作答。
【解答】解:正方体的平面展开图中,相对面的特点是中间必须间隔一个正方形,所以1和3相对,2和5相对,4和6相对,
所以与5号面相对的是2号面。
故选:B。
【名师点评】本题是考查正方体的展开图,训练学生的观察能力和空间想象能力。
8.【考点】圆锥的特征;平均数的含义及求平均数的方法;比例的意义和基本性质;辨识成正比例的量与成反比例的量.
【答案】D
【思路分析】根据题意,对各选项进行认真分析、进而得出结论.
【解答】解:A、圆锥的侧面展开图是一个等腰三角形,说法错误,应为扇形;
B、小华身高1.2米,她在平均水深是1米的水池中游泳是绝对安全的,说法错误,因为平均水深是1米,并不代表所有的地方的水深都是1米;
C、圆的面积和半径成正比例,说法错误,因为:π(一定),圆的面积应和半径的平方成正比例;
D、如果ab=cd(a、b、c、d均不为0),根据比例的基本性质可知:如果a是外项,那么b是外项,即c和d为内项,那么a:c=d:b,说法正确;
故选:D.
【名师点评】解答此题用到的知识点:(1)圆锥的特征;(2)平均数的含义;(3)比例的基本性质;(4)判断成正反比例关系的量的方法.
9.【考点】负数的意义及其应用.
【答案】A
【思路分析】此题首先要知道以10t为标准,规定超出10t的为正,低于10t的为负,由此用正负数解答问题。
【解答】解:A.8t记作﹣8t,应记作﹣2t,故说法错误;
B.15t记作+5t,说法正确;
C.6t记作﹣4t,说法正确;
D.+3t表示13t,说法正确。
故选:A。
【名师点评】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
10.【考点】小数点位置的移动与小数大小的变化规律;百分数的意义、读写及应用.
【答案】A
【思路分析】13.6%化成小数是0.136,它的小数点向右移动2位是13.6。据此解答。
【解答】解:13.6%去掉百分号后,这个数就扩大到原来的100倍。
故选:A。
【名师点评】一个数(不等于0)后面添上百分号,这个数就缩小到原来的;一个百分数去掉百分号,这个数就扩大到原来的100倍。
11.【考点】简单事件发生的可能性求解;事件的确定性与不确定性;可能性的大小.
【答案】C
【思路分析】A,妙想抛20次硬币,有可能11次正面朝上;
B,第5次抛的结果可能正面朝上,也可能反面朝上;
C,因为正面朝上和反面朝上的可能性是相等的,所以正面朝上的次数和反面朝上的次数的比值接近或等于1;
D,10次硬币,有可能8次正面朝上。
【解答】解:A,妙想抛20次硬币,有可能11次正面朝上,所以这个说法错误;
B,第5次抛的结果可能正面朝上,也可能反面朝上,所以这个说法错误;
C,因为正面朝上和反面朝上的可能性是相等的,所以正面朝上的次数和反面朝上的次数的比值接近或等于1,这个说法正确;
D,抛10次硬币,有可能8次正面朝上,所以这个说法错误。
故选:C。
【名师点评】本题考查可能性的大小,事件的确定性与不确定性知识点。
12.【考点】比的应用.
【答案】D
【思路分析】先根据三角形的内角和求出剩下的两个角的度数和,再按照比例分配即可。
【解答】解:180°﹣30°=150°
150°÷(1+4)×4
=150°÷5×4
=120°
这个三角形是钝角三角形。
故选:D。
【名师点评】先根据三角形的内角和求出剩下的两个角的度数和,是解答此题的关键。
二.填空题
13.【考点】亿以内数的读写.
【答案】一千七百五十六万零六十一,1756。
【思路分析】根据整数的读法,从高位到低位,一级一级地读,每一级末尾的0都不读出来,其余数位连续几个0都只读一个零,即可读出此数;
省略“万”后面的尾数就是四舍五入到万位,就是把万位后的千位上的数进行四舍五入,再在数的后面写上“万”字。
【解答】解:17560061读作:一千七百五十六万零六十一;17560061≈1756万。
故答案为:一千七百五十六万零六十一,1756。
【名师点评】本题主要考查整数的读法和求近似数,读数时要注意零的读法,求近似数时要注意带计数单位。
14.【考点】质量的单位换算;时、分、秒及其关系、单位换算与计算.
【答案】(1)5.06;(2)3,9。
【思路分析】(1)把60千克除以进率1000化成0.06吨,再加5吨;
(2)3.15时看作3时与0.15时之和,把0.15时乘进率60化成9分。
【解答】解:(1)5吨60千克=5.06吨;
(2)3.15时=3时9分。
故答案为:5.06;3,9。
【名师点评】本题是考查质量的单位换算、时间的单位换算。单位换算首先要弄清是由高级单位化低级单位还是由低级单位化高级单位,其次记住单位间的进率。
15.【考点】数与形结合的规律.
【答案】13;36。
【思路分析】观察图示,可发现,第(1)幅图中〇有1个,可写作:2×1﹣1;第(2)幅图中〇有3个,可写作:2×2﹣1;第(3)幅图中〇有5个,可写作:2×3﹣1;以此类推,第(7)幅图中有〇的个数是:2×7﹣1(个);
观察图示,可发现,第(1)幅图中■有0个;第(2)幅图中■有1个,可写作:12;第(3)幅图中■有4个,可写作:22;第(4)幅图中■有9个,可写作:32;以此类推,第(7)幅图中有■的个数为:62(个);据此求解即可。
【解答】解:2×7﹣1
=14﹣1
=13(个)
62=36(个)
答:第(7)幅图中有13个〇,有36个■。
故答案为:13;36。
【名师点评】本题主要考查数与形结合的规律,关键根据所给图示,找出规律,并利用规律做题。
16.【考点】求几个数的最小公倍数的方法;求几个数的最大公因数的方法.
【答案】10,210。
【思路分析】先把要求的两个数分别分解质因数,然后把它们公有的质因数连乘起来,所得的积就是它们的最大公因数,把它们公有的质因数和独有的质因数连乘起来,所得的积就是它们的最小公倍数。
【解答】解:A=2×3×5
B=2×5×7
所以A和B的最大公因数是2×5=10,最小公倍数是2×3×5×7=210。
故答案为:10,210。
【名师点评】熟练掌握求两个数最大公因数和最小公倍数的方法是解题的关键。
17.【考点】分数大小的比较.
【答案】<,>,<,>。
【思路分析】①把分数化成小数,再按照小数比较大小的方法进行比较;
②把百分数和分数都化成小数,再按照小数比较大小的方法进行比较;
③把化成带分数为2,再比较和的大小即可;
④按照整数比较大小的方法进行比较即可。
【解答】解:①
0.56<0.571
所以0.56
②38%=0.38
0.38>0.375
所以38%
③
所以22
所以
④563201>563199
0.56 38%
563201>563199
故答案为:<,>,<,>。
【名师点评】熟练掌握分数及整数比较大小的方法是解题的关键。
18.【考点】分数的意义和读写.
【答案】,。
【思路分析】第一空求具体量,每段长度=铁丝全长÷平均分的段数;第二空求分率,把全长看作单位“1”,平均分成5份,4段是其中4份,求每段是全长的几分之几,用4份÷5份;据此解答即可。
【解答】解:6÷5(米)
4
答:把一根6米长的铁丝平均截成5段,其中每段长米,4段占这根铁丝的。
故答案为:,。
【名师点评】本题主要考查分数的意义知识点,解答本题的关键是区分清楚要求的是具体量还是分率,求分率可以用取的份数除以平均分的份数。
19.【考点】用字母表示数.
【答案】(a+19),47。
【思路分析】一盒绿壳鸡蛋的价格加上19元就是一盒乌鸡蛋的价格;把a=28代入乌鸡蛋和绿鸡蛋的关系式计算即可。
【解答】解:一盒乌鸡蛋的价格是(a+19)元;
把a=28代入a+19得:
28+19=47(元)
答:一盒乌鸡蛋的价格是(a+19)元,当a=28时,一盒乌鸡蛋的价格是47元。
故答案为:(a+19),47。
【名师点评】明确一盒绿壳鸡蛋的价格加上19元就是一盒乌鸡蛋的价格是解题的关键。
20.【考点】辨识成正比例的量与成反比例的量.
【答案】正,反。
【思路分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【解答】解:A÷6=B
所以A÷B=6(一定),商一定,所以A和B成正比例;
所以xy=4×5=20(一定),乘积一定,所以x和y成反比例。
故答案为:正,反。
【名师点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
21.【考点】圆的认识与圆周率.
【答案】圆,球。
【思路分析】一条线段的一个端点不动,另一个端点旋转一周,根据点动成线的原理即可理解。
一个半圆面围绕一条直径为轴旋转一周,根据面动成体的原理即可解。
【解答】解:将一条线段的一个端点不动,另一个端点旋转一周,其轨迹所形成的图形是圆;将一个半圆形沿着它的直径旋转一周,其轨迹所形成的图形是球。
故答案为:圆,球。
【名师点评】本题考查了点、线、面、体,平面图形旋转可以得到立体图形,体现了点动成线,面动成体的运动观点。
22.【考点】比与分数、除法的关系.
【答案】见试题解答内容
【思路分析】把每个方格的边长看作“1”,则整个长方形的长是“5”,宽是“1”,根据长方形的面积计算公式“S=ab”即可求得整个图形的面积;阴影三角形的底是“3”,高是“1”,根据三角形的面积计算公式“S=ah÷2”即可求得涂色三角形的面积。长方形的面积是5×1=5,涂色三角形的面积是3×1÷2,涂色部分面积是整个图形面积的5。根据分数的基本性质,的分子、分母都乘5就是;根据比与分数的关系,3:10,再根据比的基本性质比的前、后项都乘3就是9:30;都乘12就是36:120;3÷10=0.3;把0.3的小数点向右移动两位添上百分号就是30%。
【解答】解:9:30=30%36:120=0.3。
故答案为:30,30,50,36,0.3。
【名师点评】此题主要是考查小数、分数、百分数、比之间的关系及转化。利用它们之间的关系和性质进行转化即可。求出涂色部分占整个图形的几分之几是关键。
23.【考点】比例的意义和基本性质.
【答案】2.5。
【思路分析】两个外项互为倒数,则两外项之积是1,根据比例的基本性质“在比例中,两外项之积等于两内项之积”,可得两内项之积也等于1,据此计算即可。
【解答】解:1÷0.4=2.5
答:另一个内项是2.5。
故答案为:2.5。
【名师点评】本题主要考查比例的基本性质,运用比例的基本性质是解答本题的关键。
24.【考点】比例尺.
【答案】40:1。
【思路分析】图上距离:实际距离=比例尺,据此解答即可。
【解答】解:8厘米=80毫米
80:2=40:1
答:这张图纸的比例尺是40:1。
故答案为:40:1。
【名师点评】本题考查比例尺知识点,掌握比例尺公式是解答本题的关键。
25.【考点】按比例分配应用题;三角形的分类;三角形的内角和.
【答案】锐角。
【思路分析】一个等腰三角形的两个角的度数比是2:3,这个三角形三个角的度数比可能是2:3:3,也可能是2:2:3;根据按比例分配的方法,把180度平均分成(2+3+3)份,再求出3份是多少度;把180度平均分成(2+2+3)份,再求出3份是多少度;根据计算出三角形中最大角的度数判断是什么三角形。
【解答】解:18067.5(度)
67.5度<90度
18077(度)
77度<90度
答:这个等腰三角形如果按角分是锐角三角形。
故答案为:锐角。
【名师点评】此题是考查按比例分配应用题的特点以及解答规律,先求出总份数,用它作公分母,再求出各部分占总数的几分之几,然后根据一个数乘分数的意义,用乘法解答。
26.【考点】百分率应用题.
【答案】155;70。
【思路分析】由题意可知,六年级女生1分钟跳绳达到152个为优秀,如果超过152的个数用正数表示,所以+3表示这个女生可以跳:152+3=155(个);+11表示这个女生可以跳:152+11=163(个);﹣3表示这个女生可以跳:152﹣3=149(个);0表示这个女生刚好跳152个;+5表示这个女生可以跳:152+5=157(个);+7表示这个女生可以跳:152+7=159(个);+13表示这个女生可以跳:152+13=165(个);﹣4表示这个女生可以跳:152﹣4=148(个);﹣2表示这个女生可以跳:152﹣2=150(个);0表示这个女生刚好跳152个;把所有女生的跳绳个数都加起来,再除以10,即能求出这10名女生1分钟跳绳的平均成绩;用优秀的女生人数除以10名女生,再乘以100%,即能求出这10名女生1分钟跳绳的优秀率是百分之几。
【解答】解:152+3=155(个)
152+11=163(个)
152﹣3=149(个)
152+0=152(个)
152+5=157(个)
152+7=159(个)
152+13=165(个)
152﹣4=148(个)
152﹣2=150(个)
152+0=152(个)
(155+163+149+152+157+159+165+148+150+152)÷10
=1550÷10
=155(个)
六年级女生1分钟跳绳达到152个的有:7名女生
优秀率是:7÷10×100%=70%
答:这10名女生1分钟跳绳的平均成绩是155个,这10名女生1分钟跳绳的优秀率是70%。
故答案为:155;70。
【名师点评】解决本题的关键是能根据题干的成绩表示方法求出每个女生的跳绳成绩。
三.计算题
27.【考点】小数的加法和减法;分数的加法和减法;求比值和化简比.
【答案】2.27,8 2,,。
【思路分析】根据小数、分数加法、除法的计算方法进行解答即可。
【解答】解:
5.07﹣2.8=2.27 34÷4=8 2 1
【名师点评】此题考查了小数、分数加法、除法的口算能力,注意认真解答即可。
28.【考点】分数方程求解.
【答案】x;x;x=20。
【思路分析】(1)根据比例的基本性质,把原式化为6x=2.3,然后方程的两边同时除以6求解;
(2)根据等式的性质,方程的两边同时乘5,然后方程的两边同时除以3求解;
(3)先计算0.8x+1.6x=2.4x,根据等式的性质,方程的两边同时除以2.4求解。
【解答】解:(1)2.3:6=x:
6x=2.3
6x÷6=2.36
x
(2)3x÷5=20
3x÷5×5=20×5
3x=100
3x÷3=100÷3
x
(3)0.8x+1.6x=48
2.4x=48
2.4x÷2.4=48÷2.4
x=20
【名师点评】本题考查解方程和解比例,解题的关键是掌握等式的性质与比例的基本性质:方程两边同时加上或减去相同的数,等式仍然成立;方程两边同时乘(或除以)相同的数(0除外),等式仍然成立;两个外项的积等于两个内项的积。
29.【考点】表外乘加、乘减;小数四则混合运算;分数的四则混合运算.
【答案】616,,58。
【思路分析】(1)先算乘法,再算减法;
(2)先算小括号里的减法,再算中括号里的减法,最后算括号外的除法;
(3)运用乘法分配律进行简算。
【解答】解:(1)728﹣28×4
=728﹣112
=616
(2)17÷[2﹣()]
=17÷[2]
=17
(3)33.5×0.58+6.65×5.8
=3.35×5.8+6.65×5.8
=(3.35+6.65)×5.8
=10×5.8
=58
【名师点评】本题考查了四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
四.操作题
30.【考点】数对与位置;作轴对称图形;作平移后的图形;图形的放大与缩小.
【答案】(1)2,2,7,4;
(2)右;如图:
(3)(4)如图。
【思路分析】(1)A点在第4列第4行,用数对(4,4)表示,B点在第2列第2行,用数对(2,2)表示,D点在第7列第4行,用数对(7,4)表示;
(2)将D点向右平移2格,再顺次连接4个点围成一个平行四边形,标记①;
(3)找到图形各个点,并过各点向对称轴作垂线;作垂线后延长,延长到与对应的点相同的距离;按照原来的方式连接各点得到图形②;
(4)图形2按1:2缩小后底边长2.5格,高1格,按图形②同样的形状画一个底边长2.5格,高1格的平行四边形,标记③。
【解答】解:(1)B、D点的位置用数对表示分别是:B(2,2)、D(7,4);
(2)如果将D点向右平移2格后,再顺次连接4个点可以围成一个平行四边形;如图:
(3)(4)如图。
故答案为:2,2,7,4;右。
【名师点评】本题考查了轴对称图形、图形的放大和缩小知识点,图形的放大和缩小不改变图形的形状,只改变图形的大小。
五.应用题
31.【考点】长方形、正方形的面积.
【答案】30块。
【思路分析】根据正方形的面积公式:S=a2,把数据代入公式求出每块方砖的面积,每块方砖的面积乘需要的块数就是书房地面的面积,然后用书房地面的面积除以另一种方砖的面积即可。
【解答】解:3×3×120÷36
=9×120÷36
=1080÷36
=30(块)
答:需要30块。
【名师点评】此题主要考查正方形面积公式的灵活运用,关键是熟记公式。
32.【考点】整数四则混合运算应用题.
【答案】
25%。
【思路分析】求女性舱外航天服比男性舱外航天服轻百分之几,就是求90千克比120千克少百分之几,列除法算式解答。
【解答】解:
(120﹣90)÷120
=30÷120
=0.25
=25%
答:女性舱外航天服比男性舱外航天服轻25%。
【名师点评】求一个数比另一个数多(少)百分之几,列除法算式解答。
33.【考点】圆锥的体积.
【答案】18.84平方厘米。
【思路分析】根据题意可知,把圆锥体铅锤总圆柱形容器中取出后,下降部分水的体积就等于这个圆锥的体积,根据圆柱的体积公式:V=πr2h,圆锥的体积公式:VSh,那么S=Vh,把数据代入公式解答。
【解答】解:3.14×62×0.59
=3.14×36×0.59
=56.52×3÷9
=169.56÷9
=18.84(平方厘米)
答:这个圆锥的底面积是18.84平方厘米。
【名师点评】此题主要考查圆柱的体积公式、圆锥的体积公式的灵活运用,关键是熟记公式。
34.【考点】圆锥的体积.
【答案】见试题解答内容
【思路分析】根据圆锥的体积公式:Vπr2h,把数据代入公式解答。
【解答】解:3.14×62×8
3.14×36×8
=301.44(立方厘米)
答:这个圆锥体的体积是301.44立方厘米。
【名师点评】此题主要考查圆锥体积公式的灵活运用,关键是熟记公式。
35.【考点】简单的工程问题.
【答案】10米,8米。
【思路分析】根据题意,设甲队每天修了x米,乙队每天修的长度是甲队的,即乙队每天修x米;甲队4天修4x米,乙队4天修(x×4)米,甲队修的米数+乙队修的米数=这条铁路的长度;列方程:4x+(x×4)=72,解方程,即可解答。
【解答】解:设甲队每天修x米,则乙队每天修x米。
4x+(x×4)=72
4xx=72
x=72
x=10
乙队:108(米)
答:甲队每天修10米,乙队每天修8米。
【名师点评】利用方程的实际应用,根据甲队与乙队每天修的长度之间的关系,设出未知数,找出相关的量,列方程,解方程。
36.【考点】比的应用.
【答案】黑色皮有12块,白色皮有20块。
【思路分析】把黑色皮看作3份,则同样的白色皮有5份,合计(3+5)份共计有32块,据此求出1份数,用1份数分别乘黑白皮的份数即可求出黑白皮的块数。
【解答】解:32÷(3+5)
=32÷8
=4(块)
3×4=12(块)
5×4=20(块)
答:黑色皮有12块,白色皮有20块。
【名师点评】本题考查了比的应用。
21世纪教育网(www.21cnjy.com)
2025年秋六年级数学小升初开学名校分班摸底押题卷(北师大版)
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题
1.如图中圆锥的体积与圆柱( )的体积相等.
A. B. C. D.
2.某班男生的平均身高是165厘米。请你判断,下面哪位男生最不可能是这个班的?( )
A.齐齐身高168厘米,是篮球队中锋 B.力力身高132厘米,是全班最矮的
C.青青身高165厘米,是全班最高的。 D.睿睿身高180厘米
3.用一副三角板可以画出的角是( )
A.160° B.40° C.105° D.125°
4.下面能折成正方体的是( )
A. B. C. D.
5.从侧面看是的组合体是( )
A. B. C. D.
6.下列选项中,正确的是( )
A.圆的半径和周长成正比例 B.3100÷300=31÷3=0……1
C.所有的质数都是合数 D.长方体是特殊的正方体
7.观察如图的正方体展开图,与⑤号面相对的是( )号面。
A.① B.② C.③ D.⑥
8.下面说法正确的是( )
A.圆锥的侧面展开图是一个等腰三角形
B.小华身高1.2米,她在平均水深是1米的水池中游泳是绝对安全的
C.圆的面积和半径成正比例
D.如果ab=cd(a、b、c、d均不为0),那么a:c=d:b
9.规定10t记作0t,11t记作+1t,则下列说法错误的是( )
A.8t记作﹣8t B.15t记作+5t C.6t记作﹣4t D.+3t表示13t
10.13.6%去掉百分号后,这个数就( )
A.扩大为原来的100倍 B.缩小为原来的
C.大小不变 D.无法确定
11.妙想做抛硬币的游戏(硬币是均匀的)。下列说法正确的是( )
A.妙想抛20次硬币,一定是10次正面朝上,10次反面朝上
B.妙想前4次抛的结果都是反面朝上,第5次一定会正面朝上
C.妙想做了1000次抛硬币的游戏,正面朝上的次数和反面朝上的次数的比值接近或等于1
D.妙想抛了10次硬币,不可能8次正面朝上
12.已知三角形一个角是30°,另外两个内角的度数比是1:4,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.等腰直角三角形 D.钝角三角形
二.填空题
13.深圳,简称“深”,别称“鹏城”,是国务院批复确定的中国经济特区、全国性经济中心城市和国际化城市。根据第七次全国人口普查结果,深圳市常住人口为17560061人,这个数读作 ,把这个数省略万位后面的尾数约是 万。
14.(1)5吨60千克= 吨;(2)3.15时= 时 分。
15.按照如图中四幅图的排列规律画下去第(7)幅图中有 个〇,有 个■。
16.已知A=2×3×5,B=2×5×7,那么,A和B的最大公因数是 ,A和B的最小公倍数是 。
17.在横线上填上“>”“<”或“=”。
0.56 38%
563201 563199
18.把一根6米长的铁丝平均截成5段,其中每段长 米,4段占这根铁丝的 。
19.宝安区开展“异地带货”助农项目,帮助龙川地区群众脱贫致富。一盒绿壳鸡蛋a元,一盒乌鸡蛋的价格比绿壳鸡蛋多19元,一盒乌鸡蛋的价格是 元。当a=28时,一盒乌鸡蛋的价格是_________元。
20.如果A÷6=B,那么A和B成 比例;如果,那么x和y成 比例。
21.将一条线段的一个端点不动,另一个端点旋转一周,其轨迹所形成的图形是 ;将一个半圆形沿着它的直径旋转一周,其轨迹所形成的图形是 。
22.根据如图中涂色部分与整个图形的面积关系填写右边的等式。
9: = % :120= 填小数
23.在一个比例式里,两个外项互为倒数其中一个内项是0.4,那么另一个内项是 。
24.一个电子零件的实际长度是2毫米,画在图纸上的长度是8厘米,这张图纸的比例尺是 。
25.一个等腰三角形的两个角的度数比是2:3,这个等腰三角形如果按角分是 三角形。
26.体育锻炼标准规定六年级女生1分钟跳绳达到152个为优秀,如果超过152的个数用正数表示,那么田田班上的10名女生的成绩分别记作:+3,+11,﹣3,0,+5,+7,+13,﹣4,﹣2,0。则这10名女生1分钟跳绳的平均成绩是 个,这10名女生1分钟跳绳的优秀率是 %
三.计算题
27.直接写出得数。
5.07﹣2.8= 34÷4= 1
28.解方程。
2.3:6=x: 3x÷5=20 0.8x+1.6x=48
29.用你喜欢的方法计算下面各题。
728﹣28×4 17÷[2﹣()] 33.5×0.58+6.65×5.8
四.操作题
30.(1)如图,方格中标出了A、B、C、D四个点,如果用数对表示这4个点的位置,A为(4,4)、C为(7,2)。那么B、D点的位置用数对表示分别是:B( , )、D( , )。
(2)如果将D点向 (填“左”或“右”)平移2格后,再顺次连接4个点可以围成一个平行四边形。画出这个平行四边形,我们把这个平行四边形叫做图形①。
(3)以直线a为对称轴,画出这个平行四边形的轴对称图形,得到图形②。
(4)画出图形②按1:2缩小后的图形,得到图形③。
五.应用题
31.爸爸打算给书房铺上方砖,用边长3分米的方砖需要120块,如果改用面积为36平方分米的方砖,需要多少块?
32.神舟十三号女性舱外航天服重约90千克,男性舱外航天服重约120千克,女性舱外航天服比男性舱外航天服轻百分之几?(先画示意图,再列式解答)
33.一个底面半径是6厘米的圆柱形玻璃器皿里装有一些水,水中浸没着一个高9厘米的圆锥体铅锤。当铅锤从水中取出后,水面下降了0.5厘米。这个圆锥体的底面积是多少平方厘米?
34.一个直角三角形的两条直角边分别长6厘米和8厘米,斜边的长度是10厘米,小智以8厘米长的直角边为轴旋转这个三角形,得到一个圆锥体,这个圆锥体的体积是多少立方厘米?
35.一条铁路长72米,甲乙两个工程队同时从两端开始维修,乙队每天维修的长度是甲队的,4天后修完。甲乙两队每天各修了多少米?
36.足球社团购买了一批足球,已知一个足球是由32块黑色正五边形和白色正六边形的皮块制成的,黑、白皮块的块数比是3:5,那么黑色和白色皮分别有多少块?
参考答案及试题解析
一.选择题
1.【考点】圆锥的体积;圆柱的侧面积、表面积和体积.
【答案】C
【思路分析】因为等底等高的圆柱的体积是圆锥体积的3倍,所以当圆柱与圆锥的体积相等、底面积相等时,圆柱的高是圆锥高的,据此解答.
【解答】解:124
所以,底面直径是6,高是12的圆锥与底面直径是6,高是4的圆柱的体积相等.
故选:C.
【名师点评】此题考查的目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及应用.
2.【考点】平均数的含义及求平均数的方法.
【答案】C
【思路分析】根据平均数是反应一组数据的集中趋势的量,它比最大数小,比最小数大,据此解答即可。
【解答】解:某班男生的平均身高是165厘米,青青身高165厘米,是全班最高的,所以青青最不可能是这个班的。
故选:C。
【名师点评】根据平均数的含义和求法,解答即可。
3.【考点】图形的拼组.
【答案】C
【思路分析】先明确一副三角板的六个角共有四个度数,30°,45°,60°,90°,然后进行加减运算,找到符合条件的角。
【解答】解:利用一副三角板可以画出的角有:30°,45°,60°,90°;30°+45°=75°,30°+90°=120°,45°+60°=105°,45°+90°=135°,60°+90°=150°,30°+45°+90°=165°;45°﹣30°=15°,一共可以画出11个角。因此105°的角可以利用三角板画出。
故选:C。
【名师点评】此题结合生活实际,既考查了对角和三角板的认识,又考查了同学们的完全归纳能力。
4.【考点】正方体的展开图.
【答案】C
【思路分析】根据正方体展开图的特征可知,图C符合正方体展开图的“2﹣2﹣2”结构,所以图C能折成正方体。据此解答即可。
【解答】解:符合正方体展开图的“2﹣2﹣2”结构,所以图C能折成正方体。
故选:C。
【名师点评】此题考查的目的是理解掌握正方体展开图的特征,训练学生的观察能力和空间想象能力。
5.【考点】从不同方向观察物体和几何体.
【答案】B
【思路分析】根据观察选项,侧面图形依次为,,,。
【解答】解:从侧面看是的组合体是。
故选:B。
【名师点评】本题是考查从不同方向观察物体和几何图形,关键是培养学生的观察能力。
6.【考点】辨识成正比例的量与成反比例的量;合数与质数的初步认识.
【答案】A
【思路分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例;被除数和除数都乘或除以一个相同的数(0除外),商不变,余数也同时乘或除以一个相同的数(0除外);根据质数、合数的意义判断;正方体是特殊的长方体。
【解答】解:A.圆的周长÷圆的半径=2π(一定),商一定,所以圆的半径和周长成正比例,正确;
B.3100÷300=31÷3,3100÷300=10……100,所以原题计算错误;
C.一个数只有1和它本身两个因数的数叫质数,除了1和它本身还有其它因数的数叫合数,所有的质数都不是合数,所以原题说法错误;
D.当长方体的长、宽、高相等时,就是正方体,正方体是特殊的长方体,所以原题说法错误;
故选:A。
【名师点评】本题考查了判断两个相关联的量之间成什么比例的方法、商的变化规律、质数、合数的意义以及长方体与正方体的关系。
7.【考点】正方体的展开图.
【答案】B
【思路分析】正方体的平面展开图中,相对面的特点是中间必须间隔一个正方形,据此作答。
【解答】解:正方体的平面展开图中,相对面的特点是中间必须间隔一个正方形,所以1和3相对,2和5相对,4和6相对,
所以与5号面相对的是2号面。
故选:B。
【名师点评】本题是考查正方体的展开图,训练学生的观察能力和空间想象能力。
8.【考点】圆锥的特征;平均数的含义及求平均数的方法;比例的意义和基本性质;辨识成正比例的量与成反比例的量.
【答案】D
【思路分析】根据题意,对各选项进行认真分析、进而得出结论.
【解答】解:A、圆锥的侧面展开图是一个等腰三角形,说法错误,应为扇形;
B、小华身高1.2米,她在平均水深是1米的水池中游泳是绝对安全的,说法错误,因为平均水深是1米,并不代表所有的地方的水深都是1米;
C、圆的面积和半径成正比例,说法错误,因为:π(一定),圆的面积应和半径的平方成正比例;
D、如果ab=cd(a、b、c、d均不为0),根据比例的基本性质可知:如果a是外项,那么b是外项,即c和d为内项,那么a:c=d:b,说法正确;
故选:D.
【名师点评】解答此题用到的知识点:(1)圆锥的特征;(2)平均数的含义;(3)比例的基本性质;(4)判断成正反比例关系的量的方法.
9.【考点】负数的意义及其应用.
【答案】A
【思路分析】此题首先要知道以10t为标准,规定超出10t的为正,低于10t的为负,由此用正负数解答问题。
【解答】解:A.8t记作﹣8t,应记作﹣2t,故说法错误;
B.15t记作+5t,说法正确;
C.6t记作﹣4t,说法正确;
D.+3t表示13t,说法正确。
故选:A。
【名师点评】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
10.【考点】小数点位置的移动与小数大小的变化规律;百分数的意义、读写及应用.
【答案】A
【思路分析】13.6%化成小数是0.136,它的小数点向右移动2位是13.6。据此解答。
【解答】解:13.6%去掉百分号后,这个数就扩大到原来的100倍。
故选:A。
【名师点评】一个数(不等于0)后面添上百分号,这个数就缩小到原来的;一个百分数去掉百分号,这个数就扩大到原来的100倍。
11.【考点】简单事件发生的可能性求解;事件的确定性与不确定性;可能性的大小.
【答案】C
【思路分析】A,妙想抛20次硬币,有可能11次正面朝上;
B,第5次抛的结果可能正面朝上,也可能反面朝上;
C,因为正面朝上和反面朝上的可能性是相等的,所以正面朝上的次数和反面朝上的次数的比值接近或等于1;
D,10次硬币,有可能8次正面朝上。
【解答】解:A,妙想抛20次硬币,有可能11次正面朝上,所以这个说法错误;
B,第5次抛的结果可能正面朝上,也可能反面朝上,所以这个说法错误;
C,因为正面朝上和反面朝上的可能性是相等的,所以正面朝上的次数和反面朝上的次数的比值接近或等于1,这个说法正确;
D,抛10次硬币,有可能8次正面朝上,所以这个说法错误。
故选:C。
【名师点评】本题考查可能性的大小,事件的确定性与不确定性知识点。
12.【考点】比的应用.
【答案】D
【思路分析】先根据三角形的内角和求出剩下的两个角的度数和,再按照比例分配即可。
【解答】解:180°﹣30°=150°
150°÷(1+4)×4
=150°÷5×4
=120°
这个三角形是钝角三角形。
故选:D。
【名师点评】先根据三角形的内角和求出剩下的两个角的度数和,是解答此题的关键。
二.填空题
13.【考点】亿以内数的读写.
【答案】一千七百五十六万零六十一,1756。
【思路分析】根据整数的读法,从高位到低位,一级一级地读,每一级末尾的0都不读出来,其余数位连续几个0都只读一个零,即可读出此数;
省略“万”后面的尾数就是四舍五入到万位,就是把万位后的千位上的数进行四舍五入,再在数的后面写上“万”字。
【解答】解:17560061读作:一千七百五十六万零六十一;17560061≈1756万。
故答案为:一千七百五十六万零六十一,1756。
【名师点评】本题主要考查整数的读法和求近似数,读数时要注意零的读法,求近似数时要注意带计数单位。
14.【考点】质量的单位换算;时、分、秒及其关系、单位换算与计算.
【答案】(1)5.06;(2)3,9。
【思路分析】(1)把60千克除以进率1000化成0.06吨,再加5吨;
(2)3.15时看作3时与0.15时之和,把0.15时乘进率60化成9分。
【解答】解:(1)5吨60千克=5.06吨;
(2)3.15时=3时9分。
故答案为:5.06;3,9。
【名师点评】本题是考查质量的单位换算、时间的单位换算。单位换算首先要弄清是由高级单位化低级单位还是由低级单位化高级单位,其次记住单位间的进率。
15.【考点】数与形结合的规律.
【答案】13;36。
【思路分析】观察图示,可发现,第(1)幅图中〇有1个,可写作:2×1﹣1;第(2)幅图中〇有3个,可写作:2×2﹣1;第(3)幅图中〇有5个,可写作:2×3﹣1;以此类推,第(7)幅图中有〇的个数是:2×7﹣1(个);
观察图示,可发现,第(1)幅图中■有0个;第(2)幅图中■有1个,可写作:12;第(3)幅图中■有4个,可写作:22;第(4)幅图中■有9个,可写作:32;以此类推,第(7)幅图中有■的个数为:62(个);据此求解即可。
【解答】解:2×7﹣1
=14﹣1
=13(个)
62=36(个)
答:第(7)幅图中有13个〇,有36个■。
故答案为:13;36。
【名师点评】本题主要考查数与形结合的规律,关键根据所给图示,找出规律,并利用规律做题。
16.【考点】求几个数的最小公倍数的方法;求几个数的最大公因数的方法.
【答案】10,210。
【思路分析】先把要求的两个数分别分解质因数,然后把它们公有的质因数连乘起来,所得的积就是它们的最大公因数,把它们公有的质因数和独有的质因数连乘起来,所得的积就是它们的最小公倍数。
【解答】解:A=2×3×5
B=2×5×7
所以A和B的最大公因数是2×5=10,最小公倍数是2×3×5×7=210。
故答案为:10,210。
【名师点评】熟练掌握求两个数最大公因数和最小公倍数的方法是解题的关键。
17.【考点】分数大小的比较.
【答案】<,>,<,>。
【思路分析】①把分数化成小数,再按照小数比较大小的方法进行比较;
②把百分数和分数都化成小数,再按照小数比较大小的方法进行比较;
③把化成带分数为2,再比较和的大小即可;
④按照整数比较大小的方法进行比较即可。
【解答】解:①
0.56<0.571
所以0.56
②38%=0.38
0.38>0.375
所以38%
③
所以22
所以
④563201>563199
0.56 38%
563201>563199
故答案为:<,>,<,>。
【名师点评】熟练掌握分数及整数比较大小的方法是解题的关键。
18.【考点】分数的意义和读写.
【答案】,。
【思路分析】第一空求具体量,每段长度=铁丝全长÷平均分的段数;第二空求分率,把全长看作单位“1”,平均分成5份,4段是其中4份,求每段是全长的几分之几,用4份÷5份;据此解答即可。
【解答】解:6÷5(米)
4
答:把一根6米长的铁丝平均截成5段,其中每段长米,4段占这根铁丝的。
故答案为:,。
【名师点评】本题主要考查分数的意义知识点,解答本题的关键是区分清楚要求的是具体量还是分率,求分率可以用取的份数除以平均分的份数。
19.【考点】用字母表示数.
【答案】(a+19),47。
【思路分析】一盒绿壳鸡蛋的价格加上19元就是一盒乌鸡蛋的价格;把a=28代入乌鸡蛋和绿鸡蛋的关系式计算即可。
【解答】解:一盒乌鸡蛋的价格是(a+19)元;
把a=28代入a+19得:
28+19=47(元)
答:一盒乌鸡蛋的价格是(a+19)元,当a=28时,一盒乌鸡蛋的价格是47元。
故答案为:(a+19),47。
【名师点评】明确一盒绿壳鸡蛋的价格加上19元就是一盒乌鸡蛋的价格是解题的关键。
20.【考点】辨识成正比例的量与成反比例的量.
【答案】正,反。
【思路分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【解答】解:A÷6=B
所以A÷B=6(一定),商一定,所以A和B成正比例;
所以xy=4×5=20(一定),乘积一定,所以x和y成反比例。
故答案为:正,反。
【名师点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
21.【考点】圆的认识与圆周率.
【答案】圆,球。
【思路分析】一条线段的一个端点不动,另一个端点旋转一周,根据点动成线的原理即可理解。
一个半圆面围绕一条直径为轴旋转一周,根据面动成体的原理即可解。
【解答】解:将一条线段的一个端点不动,另一个端点旋转一周,其轨迹所形成的图形是圆;将一个半圆形沿着它的直径旋转一周,其轨迹所形成的图形是球。
故答案为:圆,球。
【名师点评】本题考查了点、线、面、体,平面图形旋转可以得到立体图形,体现了点动成线,面动成体的运动观点。
22.【考点】比与分数、除法的关系.
【答案】见试题解答内容
【思路分析】把每个方格的边长看作“1”,则整个长方形的长是“5”,宽是“1”,根据长方形的面积计算公式“S=ab”即可求得整个图形的面积;阴影三角形的底是“3”,高是“1”,根据三角形的面积计算公式“S=ah÷2”即可求得涂色三角形的面积。长方形的面积是5×1=5,涂色三角形的面积是3×1÷2,涂色部分面积是整个图形面积的5。根据分数的基本性质,的分子、分母都乘5就是;根据比与分数的关系,3:10,再根据比的基本性质比的前、后项都乘3就是9:30;都乘12就是36:120;3÷10=0.3;把0.3的小数点向右移动两位添上百分号就是30%。
【解答】解:9:30=30%36:120=0.3。
故答案为:30,30,50,36,0.3。
【名师点评】此题主要是考查小数、分数、百分数、比之间的关系及转化。利用它们之间的关系和性质进行转化即可。求出涂色部分占整个图形的几分之几是关键。
23.【考点】比例的意义和基本性质.
【答案】2.5。
【思路分析】两个外项互为倒数,则两外项之积是1,根据比例的基本性质“在比例中,两外项之积等于两内项之积”,可得两内项之积也等于1,据此计算即可。
【解答】解:1÷0.4=2.5
答:另一个内项是2.5。
故答案为:2.5。
【名师点评】本题主要考查比例的基本性质,运用比例的基本性质是解答本题的关键。
24.【考点】比例尺.
【答案】40:1。
【思路分析】图上距离:实际距离=比例尺,据此解答即可。
【解答】解:8厘米=80毫米
80:2=40:1
答:这张图纸的比例尺是40:1。
故答案为:40:1。
【名师点评】本题考查比例尺知识点,掌握比例尺公式是解答本题的关键。
25.【考点】按比例分配应用题;三角形的分类;三角形的内角和.
【答案】锐角。
【思路分析】一个等腰三角形的两个角的度数比是2:3,这个三角形三个角的度数比可能是2:3:3,也可能是2:2:3;根据按比例分配的方法,把180度平均分成(2+3+3)份,再求出3份是多少度;把180度平均分成(2+2+3)份,再求出3份是多少度;根据计算出三角形中最大角的度数判断是什么三角形。
【解答】解:18067.5(度)
67.5度<90度
18077(度)
77度<90度
答:这个等腰三角形如果按角分是锐角三角形。
故答案为:锐角。
【名师点评】此题是考查按比例分配应用题的特点以及解答规律,先求出总份数,用它作公分母,再求出各部分占总数的几分之几,然后根据一个数乘分数的意义,用乘法解答。
26.【考点】百分率应用题.
【答案】155;70。
【思路分析】由题意可知,六年级女生1分钟跳绳达到152个为优秀,如果超过152的个数用正数表示,所以+3表示这个女生可以跳:152+3=155(个);+11表示这个女生可以跳:152+11=163(个);﹣3表示这个女生可以跳:152﹣3=149(个);0表示这个女生刚好跳152个;+5表示这个女生可以跳:152+5=157(个);+7表示这个女生可以跳:152+7=159(个);+13表示这个女生可以跳:152+13=165(个);﹣4表示这个女生可以跳:152﹣4=148(个);﹣2表示这个女生可以跳:152﹣2=150(个);0表示这个女生刚好跳152个;把所有女生的跳绳个数都加起来,再除以10,即能求出这10名女生1分钟跳绳的平均成绩;用优秀的女生人数除以10名女生,再乘以100%,即能求出这10名女生1分钟跳绳的优秀率是百分之几。
【解答】解:152+3=155(个)
152+11=163(个)
152﹣3=149(个)
152+0=152(个)
152+5=157(个)
152+7=159(个)
152+13=165(个)
152﹣4=148(个)
152﹣2=150(个)
152+0=152(个)
(155+163+149+152+157+159+165+148+150+152)÷10
=1550÷10
=155(个)
六年级女生1分钟跳绳达到152个的有:7名女生
优秀率是:7÷10×100%=70%
答:这10名女生1分钟跳绳的平均成绩是155个,这10名女生1分钟跳绳的优秀率是70%。
故答案为:155;70。
【名师点评】解决本题的关键是能根据题干的成绩表示方法求出每个女生的跳绳成绩。
三.计算题
27.【考点】小数的加法和减法;分数的加法和减法;求比值和化简比.
【答案】2.27,8 2,,。
【思路分析】根据小数、分数加法、除法的计算方法进行解答即可。
【解答】解:
5.07﹣2.8=2.27 34÷4=8 2 1
【名师点评】此题考查了小数、分数加法、除法的口算能力,注意认真解答即可。
28.【考点】分数方程求解.
【答案】x;x;x=20。
【思路分析】(1)根据比例的基本性质,把原式化为6x=2.3,然后方程的两边同时除以6求解;
(2)根据等式的性质,方程的两边同时乘5,然后方程的两边同时除以3求解;
(3)先计算0.8x+1.6x=2.4x,根据等式的性质,方程的两边同时除以2.4求解。
【解答】解:(1)2.3:6=x:
6x=2.3
6x÷6=2.36
x
(2)3x÷5=20
3x÷5×5=20×5
3x=100
3x÷3=100÷3
x
(3)0.8x+1.6x=48
2.4x=48
2.4x÷2.4=48÷2.4
x=20
【名师点评】本题考查解方程和解比例,解题的关键是掌握等式的性质与比例的基本性质:方程两边同时加上或减去相同的数,等式仍然成立;方程两边同时乘(或除以)相同的数(0除外),等式仍然成立;两个外项的积等于两个内项的积。
29.【考点】表外乘加、乘减;小数四则混合运算;分数的四则混合运算.
【答案】616,,58。
【思路分析】(1)先算乘法,再算减法;
(2)先算小括号里的减法,再算中括号里的减法,最后算括号外的除法;
(3)运用乘法分配律进行简算。
【解答】解:(1)728﹣28×4
=728﹣112
=616
(2)17÷[2﹣()]
=17÷[2]
=17
(3)33.5×0.58+6.65×5.8
=3.35×5.8+6.65×5.8
=(3.35+6.65)×5.8
=10×5.8
=58
【名师点评】本题考查了四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
四.操作题
30.【考点】数对与位置;作轴对称图形;作平移后的图形;图形的放大与缩小.
【答案】(1)2,2,7,4;
(2)右;如图:
(3)(4)如图。
【思路分析】(1)A点在第4列第4行,用数对(4,4)表示,B点在第2列第2行,用数对(2,2)表示,D点在第7列第4行,用数对(7,4)表示;
(2)将D点向右平移2格,再顺次连接4个点围成一个平行四边形,标记①;
(3)找到图形各个点,并过各点向对称轴作垂线;作垂线后延长,延长到与对应的点相同的距离;按照原来的方式连接各点得到图形②;
(4)图形2按1:2缩小后底边长2.5格,高1格,按图形②同样的形状画一个底边长2.5格,高1格的平行四边形,标记③。
【解答】解:(1)B、D点的位置用数对表示分别是:B(2,2)、D(7,4);
(2)如果将D点向右平移2格后,再顺次连接4个点可以围成一个平行四边形;如图:
(3)(4)如图。
故答案为:2,2,7,4;右。
【名师点评】本题考查了轴对称图形、图形的放大和缩小知识点,图形的放大和缩小不改变图形的形状,只改变图形的大小。
五.应用题
31.【考点】长方形、正方形的面积.
【答案】30块。
【思路分析】根据正方形的面积公式:S=a2,把数据代入公式求出每块方砖的面积,每块方砖的面积乘需要的块数就是书房地面的面积,然后用书房地面的面积除以另一种方砖的面积即可。
【解答】解:3×3×120÷36
=9×120÷36
=1080÷36
=30(块)
答:需要30块。
【名师点评】此题主要考查正方形面积公式的灵活运用,关键是熟记公式。
32.【考点】整数四则混合运算应用题.
【答案】
25%。
【思路分析】求女性舱外航天服比男性舱外航天服轻百分之几,就是求90千克比120千克少百分之几,列除法算式解答。
【解答】解:
(120﹣90)÷120
=30÷120
=0.25
=25%
答:女性舱外航天服比男性舱外航天服轻25%。
【名师点评】求一个数比另一个数多(少)百分之几,列除法算式解答。
33.【考点】圆锥的体积.
【答案】18.84平方厘米。
【思路分析】根据题意可知,把圆锥体铅锤总圆柱形容器中取出后,下降部分水的体积就等于这个圆锥的体积,根据圆柱的体积公式:V=πr2h,圆锥的体积公式:VSh,那么S=Vh,把数据代入公式解答。
【解答】解:3.14×62×0.59
=3.14×36×0.59
=56.52×3÷9
=169.56÷9
=18.84(平方厘米)
答:这个圆锥的底面积是18.84平方厘米。
【名师点评】此题主要考查圆柱的体积公式、圆锥的体积公式的灵活运用,关键是熟记公式。
34.【考点】圆锥的体积.
【答案】见试题解答内容
【思路分析】根据圆锥的体积公式:Vπr2h,把数据代入公式解答。
【解答】解:3.14×62×8
3.14×36×8
=301.44(立方厘米)
答:这个圆锥体的体积是301.44立方厘米。
【名师点评】此题主要考查圆锥体积公式的灵活运用,关键是熟记公式。
35.【考点】简单的工程问题.
【答案】10米,8米。
【思路分析】根据题意,设甲队每天修了x米,乙队每天修的长度是甲队的,即乙队每天修x米;甲队4天修4x米,乙队4天修(x×4)米,甲队修的米数+乙队修的米数=这条铁路的长度;列方程:4x+(x×4)=72,解方程,即可解答。
【解答】解:设甲队每天修x米,则乙队每天修x米。
4x+(x×4)=72
4xx=72
x=72
x=10
乙队:108(米)
答:甲队每天修10米,乙队每天修8米。
【名师点评】利用方程的实际应用,根据甲队与乙队每天修的长度之间的关系,设出未知数,找出相关的量,列方程,解方程。
36.【考点】比的应用.
【答案】黑色皮有12块,白色皮有20块。
【思路分析】把黑色皮看作3份,则同样的白色皮有5份,合计(3+5)份共计有32块,据此求出1份数,用1份数分别乘黑白皮的份数即可求出黑白皮的块数。
【解答】解:32÷(3+5)
=32÷8
=4(块)
3×4=12(块)
5×4=20(块)
答:黑色皮有12块,白色皮有20块。
【名师点评】本题考查了比的应用。
21世纪教育网(www.21cnjy.com)
同课章节目录
