(小升初开学分班考)小升初开学名校分班摸底培优卷-2025年秋六年级数学北师大版(含答案解析)
文档属性
| 名称 | (小升初开学分班考)小升初开学名校分班摸底培优卷-2025年秋六年级数学北师大版(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 145.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-16 00:31:21 | ||
图片预览




文档简介
/ 让学习更有效 小升初备考 | 数学学科
2025年秋六年级数学小升初开学名校分班摸底培优卷(北师大版)
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题
1.不能与组成比例的是( )
A.16:12 B.3:4 C.1: D.0.8:0.6
2.一个三角形有三个锐角,其中一个角是60°,这个三角形一定是( )
A.等边三角形 B.直角三角形 C.锐角三角形 D.无法确定
3.以下说法正确的是( )
A.人的近视度数和年龄成正比例。
B.A+B=100,那么A和B成反比例。
C.(M+2)x=y,且x和y都不为0,当M一定时,x和y不成比例。
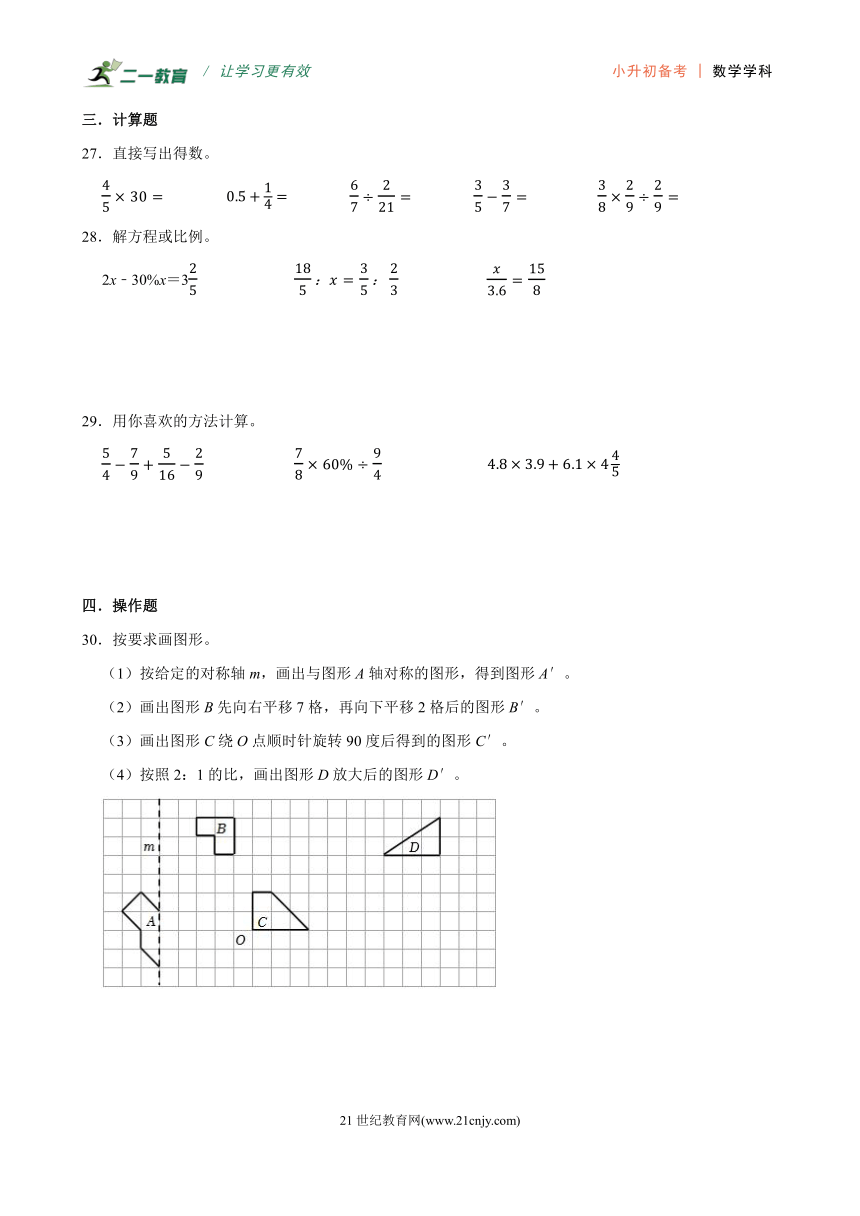
D.圆锥的高一定,体积和底面积成正比例。
4.圆周率是圆的周长与直径的比值,公元263年,中国数学家刘徽用“割圆术”计算圆周率,公元480年左右,南北朝数学家祖冲之进一步得到圆周率小数点后7位的结果。如果如图中线段AF表示一个圆的周长,那么这个圆的直径可能是( )
A.线段AB B.线段AC C.线段AD D.线段CE
5.一个三角形有两个内角分别是50°和80°,它是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.无法确定
6.一个电子零件的实际长度是2毫米,画在图纸上的长度是8厘米,这张图纸的比例尺是( )
A.1:4 B.4:1 C.40:1 D.1:40
7.用2、5、8三张数字卡片摆三位数,这些三位数都是( )
A.2的倍数 B.3的倍数 C.5的倍数 D.以上答案都不对
8.张华用5cm、8cm和4cm的木棒首尾相接拼了一个三角形,李明也用同样的3根小棒,首尾相接拼了一个三角形,李明拼的三角形和张华的相比,( )
A.形状相同,大小相等 B.形状相同,大小不等
C.形状不同,大小不等 D.形状不同,大小相等
9.将0.75转换为分数,这些分数的分子和分母都是小于30的自然数,这样的分数共有( )个。
A.3 B.5 C.7 D.9
10.一个立体图形从上面看是,从左面看是,从前面看是,这个立体图形是( )
A. B. C. D.
11.下列各组数中,不能通过加、减,乘、除(含括号)运算得到24的是( )
A.1,1,7,7 B.2,2,8,8 C.1,1,2,8 D.1,1,4,6
12.如图四个图通过平移排成一横行,彼此之间没有空隙,正确的排列顺序是( )
A.③②①④ B.②①④③ C.①③④② D.④②①③
二.填空题
13.摄氏温度和华氏温度的关系是T℉=1.8t℃+32(t为摄氏温度数,T为华氏温度数)。如果一个人的体温是37℃,那么这个人的体温转化成华氏温度是 ℉。
14.根据世卫组织最新实时统计数据,截至欧洲中部夏令时间6月14日18时13分(北京时间6月15日0时13分),全球累计新冠肺炎确诊病例533816957例,533816957读作 ,改写成以“万”为单位的数是 万,四舍五入到亿位约是 亿。
15.如图中的7个点连在一起形成了两个完全一样的长方形,其中2个点的位置用数对表示分别是(1,5)、(5,1)请写出A点和B点的数对。
A点的数对是( , );B点的数对是( , )。
16.18的因数有 ,选出其中四个数组成一个比例是 。
17.一个圆柱的底面积是15cm2,高是8cm,这个圆柱的体积是 cm3。
18.把改写成乘法算式是 ,当a=123时,算式结果是 。
19.把一根圆柱形钢材切削成一个最大的圆锥,切削掉部分的体积为8dm3,这根圆柱形钢材的体积是______ dm3。
20.六(1)班师生46人去野营,一共租了10顶帐篷,正好住满。每顶大帐篷住5人,每顶小帐篷住3人。大帐篷有 顶,小帐篷有 顶。
21.如图,把左边的三角形按比例缩小后得到右边的三角形,则x= 。
22.如图,小朋友在玩“老狼捉小羊”的游戏。以老狼所在的位置为观测点,小羊A在老狼的 偏 , °方向上,小羊B在老狼的 偏 , °方向上。
23.盒子里装有三种除颜色外其它完全相同的球,黄色有9个,红色有5个,白色有2个,任意摸出一个球,摸出 色球的可能性最大。
24.将一条线段的一个端点不动,另一个端点旋转一周,其轨迹所形成的图形是 ;将一个半圆形沿着它的直径旋转一周,其轨迹所形成的图形是 。
25.在一个比例式里,两个外项互为倒数其中一个内项是0.4,那么另一个内项是 。
26.根据如图中涂色部分与整个图形的面积关系填写右边的等式。
9: = % :120= 填小数
三.计算题
27.直接写出得数。
28.解方程或比例。
2x﹣30%x=3
29.用你喜欢的方法计算。
四.操作题
30.按要求画图形。
(1)按给定的对称轴m,画出与图形A轴对称的图形,得到图形A′。
(2)画出图形B先向右平移7格,再向下平移2格后的图形B′。
(3)画出图形C绕O点顺时针旋转90度后得到的图形C′。
(4)按照2:1的比,画出图形D放大后的图形D′。
五.应用题
31.一个圆锥形的沙堆,底面半径是2米,高是1.5米,如果把这些沙子铺在长4米,宽2米的长方体沙坑内,可以铺多高?
32.淘气家装修厨房,原计划用边长2分米的方砖,需要270块。如果改用面积为0.09平方米的方砖铺,需要多少块呢?
33.一个圆柱体的高是12厘米,如果将这个圆柱体的高减少,那么它的表面积就减少37.68平方厘米,原来圆柱体的体积是多少立方厘米?
34.2023年5月10日,我国天舟六号“太空快递”发射成功。天舟六号货运飞船的载货能力达到了7400千克,约是天舟一号货运飞船载货能力的,天舟一号货运飞船的载货能力约是多少千克?
35.6月26日是国际禁毒日,阳光小学组织了以“珍爱生命拒绝毒品”为主题的绘画创作大赛,六(2)班提交了24件作品,六(1)班提交的作品比六(2)班少25%,六(1)班提交了多少件作品?
36.如图,圆柱体容器中有628毫升的水,乌鸦至少要衔多少立方厘米的石子放进容器中才能喝到水?
参考答案及试题解析
一.选择题
1.【考点】比例的意义和基本性质.
【答案】B
【思路分析】比例的基本概念,比值相等的两个比组成比例,算出各项的比值,据此判断即可。
【解答】解::
A.16:12
B.3:4
C.1:
D.0.8:0.6
:和3:4的比值不相等,所以不能组成比例。
故选:B。
【名师点评】此题需要学生熟练掌握比例的意义并灵活运用。
2.【考点】三角形的分类.
【答案】C
【思路分析】根据三角形的分类知识可知,三个角都是锐角的三角形是锐角三角形,据此解答即可。
【解答】解:三角形有三个锐角,其中一个角是60°,这个三角形一定是锐角三角形。
故选:C。
【名师点评】本题考查了三角形的分类知识,结合题意分析解答即可。
3.【考点】辨识成正比例的量与成反比例的量.
【答案】D
【思路分析】两种相关联的量,若两种量的比值一定,两种量成正比例;若两种量的乘积一定,两种量成反比例。
【解答】解:选项A中,人的近视度数和年龄不是相关联的量,人的近视度数和年龄不成比例。原题说法错误。
选项B中,A+B=100,A与B的和一定,A与B不成比例。原题说法错误。
选项C中,由(M+2)x=y,可得M+2,当M一定时,y和x的比值一定,y和x成正比例。原题说法错误。
选项D 中,圆锥的高=3×体积÷底面积,圆锥的高一定,体积和底面积的商一定,体积和底面积成正比例。原题说法正确。
故选:D。
【名师点评】辨识两种相关联的量成正比例还是成反比例,就看两种量的比值一定还是乘积一定。
4.【考点】圆的认识与圆周率.
【答案】D
【思路分析】根据圆周率的含义:圆的周长和它直径的比值,叫做圆周率,圆周率用π表示,根据圆的周长=直径乘π,即C=πd,直径为d,那么周长与直径的比值即是π。因为π的近似值是3.14,所以图中线段AF代表一个圆的周长的话,那么这个圆的直径大约是周长的三分之一,据此解答即可。
【解答】解:根据圆的周长=直径乘π,即C=πd,C÷d=π,π≈3.14,图中线段AF代表一个圆的周长,则圆的直径大约是周长的三分之一,根据图示线段CE最适合。
故选:D。
【名师点评】此题解答关键是明确π大约等于3.14,周长大约是直径的三倍。
5.【考点】三角形的内角和;等腰三角形与等边三角形.
【答案】A
【思路分析】先根据三角形内角和定理求出另一个角的度数,进而可得出结论。
【解答】解:因为一个三角形的两个内角分别是50°、80°,
所以此三角形另一个内角=180°﹣80°﹣50°=50°,
所以它是等腰三角形。
故选:A。
【名师点评】本题考查的是三角形内角和定理,熟知“三角形内角和是180°”是解答此题的关键。
6.【考点】比例尺.
【答案】C
【思路分析】根据比例尺的意义作答,即图上距离与实际距离的比。
【解答】解:2毫米=0.2厘米
8:0.2
=(8÷0.2):(0.2÷0.2)
=40:1
答:这张图纸的比例尺是40:1。
故选:C。
【名师点评】本题主要考查了比例尺的意义,注意图上距离与实际距离的单位要统一。
7.【考点】2、3、5的倍数特征.
【答案】B
【思路分析】个位上是0,2,4,6,8的数是2的倍数;个位上是0或5的数是5的倍数;如果一个数的各个数位上的数的和是3的倍数,那么这个数就是3的倍数。
【解答】解:2+5+8=15,15是3的倍数,所以这些三位数都是3的倍数。
故选:B。
【名师点评】熟练掌握2、3、5的倍数的特征是解决此题的关键。
8.【考点】三角形的特性.
【答案】A
【思路分析】根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边,因为三边都相等,所以围成的图形形状相同,大小也相等;由此解答即可。
【解答】解:因为4+5>8,所以能摆成三角形,且形状相同,大小相等。
故选:A。
【名师点评】本题考查了三角形的特性,注意任意两边之和大于第三边,任意两边之差小于第三边。
9.【考点】小数与分数的互化.
【答案】C
【思路分析】小数化成分数:原来有几位小数,就在1的后面写几个零作分母,把原来的小数去掉小数点作分子,能约分的要约分;再根据分数的基本性质即可求解。
【解答】解:0.75
30÷4=7......2
答:这样的分数共有7个。
故选:C。
【名师点评】本题考查了小数与分数的互化,关键是熟练掌握小数化成分数的方法。
10.【考点】从不同方向观察物体和几何体.
【答案】B
【思路分析】根据从上面、左面和前面看到的形状可知,该几何体由8个小正方体拼成,下层6个分两行,上面一行4个,下面一行2个,左右齐;上面一层2个,分别在下层后排左起第2个的上面和前排右面的上面。据此解答。
【解答】解:一个立体图形从上面看是,从左面看是,从前面看是,这个立体图形是。
故选:B。
【名师点评】本题是考查从不同方向观察物体和几何图形,关键是培养学生的观察能力。
11.【考点】带括号的表内除加、除减.
【答案】A
【思路分析】24点是4个数通过四则运算、括号得到24的一种数学游戏。分别尝试A、B、C、D中的数字,发现A中的数据不能通过加、减,乘、除(含括号)运算得到24。
【解答】解:A.1,1,7,7不能通过加、减,乘、除(含括号)运算得到24
B.(8﹣2)×(8÷2)=6×4=24
C.8×(2+1)÷1=8×3÷1=24
D.(4×1)×(6×1)=4×6=24
所以只有选项A不能通过加、减,乘、除(含括号)运算得到24。
故选:A。
【名师点评】本题考查填符号组算式。数通过四则运算、括号得到24即可。
12.【考点】平移.
【答案】D
【思路分析】根据图形连接点的特征排列即可。
【解答】解:四个图通过平移排成一横行,彼此之间没有空隙,正确的排列顺序是:④②①③。
故选:D。
【名师点评】本题主要考查了平移,解题的关键是观察图形的连接点。
二.填空题
13.【考点】含字母式子的求值.
【答案】98.6℉。
【思路分析】根据摄氏温度和华氏温度的关系是T℉=1.8t℃+32(t为摄氏温度数,T为华氏温度数),所以只要把一个量代入就可以求另外一个量。
【解答】解:已知一个人的体温是37℃,所以代入公式可得:
T℉=1.8×37℃+32
=66.6℃+32
=98.6℉
故答案为:98.6℉。
【名师点评】此题考查了摄氏温度和华氏温度关系的转换,只需代入公式计算就可以了。
14.【考点】亿以上数的改写与近似;亿以内数的改写与近似.
【答案】见试题解答内容
【思路分析】根据整数的读法,从高位起一级一积地往下读,读完亿级的数后面加一个“亿”字,读完万级里数后面加一个“万”字,再读个级里数;把一个数改写成用“万”作单位的数,在万万位是右下角点上小数点,后面写上万字,利用“四舍五入”法,熟练亿为后面尾数求近似数,根据千万位上数字的大小确定用“四舍”、还是用“五入”,据此解答即可。
【解答】解:533816957读作:五亿三千三百八十一万六千九百五十七;
533816957=53381.6957万
533816957≈5亿
故答案为:五亿三千三百八十一万六千九百五十七;53381.6957;5。
【名师点评】此题考查的目的是理解掌握整数的读法及应用,整数的改写方法、利用“四舍五入”省略亿位后面的尾数求近似数的方法及应用。
15.【考点】数对与位置.
【答案】5,3;9,1。
【思路分析】数对(1,5)表示的点取名为C点、数对(5,1)表示的点取名为D点;A点所在的行在C点和D点所在行的正中间,用C点和D点行数的和再除以2,可得A点的行数,A点所在的列与D点所在的列相同;B行所在的行与D点所在的行相同,B点所在列数比D点的列数多的值等于D点列数比C点列数多的值;据此解答即可。
【解答】解:数对(1,5)表示的点取名为C点、数对(5,1)表示的点取名为D点;
A点所在的列与D点所在的列相同,在第5列,
A点所在的行:(5+1)÷2=3,
A点用数对表示是(5,3);
B点所在列:5+(5﹣1)=9,
B点所在行与D点所在行相同,在第1行,
B点用数对表示是(9,1)。
故答案为:5,3;9,1。
【名师点评】本题考查数对知识点,用数对表示位置时,前面一个数表示列,后面一个数表示行。
16.【考点】比例的意义和基本性质.
【答案】见试题解答内容
【思路分析】一个数的因数的个数是有限的最小的是1,最大的是它本身;比例的意义是:表示两个比相等的式子叫作比例;由此解答。
【解答】解:18的因数有:1、2、3、6、9、18;
组成一个比例是:1:2=3:6(答案不唯一)。
故答案为:1、2、3、6、9、18;1:2=3:6(答案不唯一)。
【名师点评】此题主要根据求一个数的因数的方法和比例的意义解答。
17.【考点】圆柱的侧面积、表面积和体积.
【答案】120。
【思路分析】圆柱的体积公式V=Sh,据此代入数据计算即可。
【解答】解:15×8=120(立方厘米)
答:这个圆柱的体积是120cm3。
故答案为:120。
【名师点评】本题考查了圆柱体积公式的应用。
18.【考点】用字母表示数;含字母式子的求值.
【答案】见试题解答内容
【思路分析】表示a个相加的和是多少,即a;
当a=123时,代入a求出结果即可。
【解答】解:把改写成乘法算式是a,当a=123时,算式结果是41。
故答案为:a,41。
【名师点评】分数乘整数的意义,与整数乘法的意义相同,表示求几个相同加数的和是多少。
19.【考点】圆柱的侧面积、表面积和体积.
【答案】见试题解答内容
【思路分析】把一根圆柱形钢材切削成一个最大的圆锥,说明圆柱和圆锥等底等高,圆柱的体积是圆锥体积的3倍,削去部分的体积是圆锥体积的(3﹣1)倍,利用圆柱的体积除以2即可求出圆锥的体积,再利用圆锥的体积乘3即可。
【解答】解:8÷(3﹣1)
=8÷2
=4(立方分米)
4×3=12(立方分米)
答:这根圆柱形钢材的体积是12dm3。
故答案为:12。
【名师点评】本题考查了等底等高圆柱体积与圆锥体积之间的关系。
20.【考点】鸡兔同笼.
【答案】见试题解答内容
【思路分析】设10顶帐篷都是大帐篷,则一共可以住:10×5=50(人),这比实际的46人多50﹣46=4(人),又因为每顶大帐篷比小帐篷多住5﹣3=2(人),所以小帐篷有:4÷2=2(顶),进而求出大帐篷个数即可。
【解答】解:设10顶帐篷都是大帐篷。
小帐篷顶数:
(10×5﹣46)÷(5﹣3)
=4÷2
=2(顶)
大帐篷顶数:
10﹣2=8(顶)
所以大帐篷有8顶,小帐篷有2顶。
故答案为:8;2。
【名师点评】此题属于鸡兔同笼问题,解这类题的关键是用假设法进行分析,进而得出结论;也可以用方程进行解答。
21.【考点】图形的放大与缩小.
【答案】见试题解答内容
【思路分析】根据三角形的高的比可求出三角形缩小的比例,利用比例求出缩小后的底是多少即可。
【解答】解:3:4.8=1:1.6=5:8
说明三角形是按5:8进行缩小的,缩小后的底是原来三角形底的:
6.44
因此x等于4。
故答案为:4。
【名师点评】解答此题的关键是根据高的长度求出三角形的缩小比例。
22.【考点】根据方向和距离确定物体的位置.
【答案】见试题解答内容
【思路分析】在地图上按照“上北下南,左西右东”确定方向,注意观测点是老狼所在的位置。
【解答】解:小朋友在玩“老狼捉小羊”的游戏。以老狼所在的位置为观测点,小羊A在老狼的北偏西,45°方向上,小羊B在老狼的北偏东,45°方向上。
故答案为:北,西,45,北,东,45。
【名师点评】本题主要考查学生的方位感和对基本方向的辨别。
23.【考点】可能性的大小.
【答案】黄。
【思路分析】在这个盒子里面一共有三种颜色的球,黄色球的数量最多,白色球的数量最少,同种颜色多的球摸到的可能性大,同种颜色少的球摸到的可能性小。
【解答】解:盒子里装有三种除颜色外其它完全相同的球,黄色有9个,红色有5个,白色有2个,任意摸出一个球,摸出黄色球的可能性最大。
故答案为:黄。
【名师点评】本题考查可能性大小的判断,解题关键是理解并掌握影响可能性大小的因素,理解哪种颜色的球多,摸到哪种球的可能性就大。
24.【考点】圆的认识与圆周率.
【答案】圆,球。
【思路分析】一条线段的一个端点不动,另一个端点旋转一周,根据点动成线的原理即可理解。
一个半圆面围绕一条直径为轴旋转一周,根据面动成体的原理即可解。
【解答】解:将一条线段的一个端点不动,另一个端点旋转一周,其轨迹所形成的图形是圆;将一个半圆形沿着它的直径旋转一周,其轨迹所形成的图形是球。
故答案为:圆,球。
【名师点评】本题考查了点、线、面、体,平面图形旋转可以得到立体图形,体现了点动成线,面动成体的运动观点。
25.【考点】比例的意义和基本性质.
【答案】2.5。
【思路分析】两个外项互为倒数,则两外项之积是1,根据比例的基本性质“在比例中,两外项之积等于两内项之积”,可得两内项之积也等于1,据此计算即可。
【解答】解:1÷0.4=2.5
答:另一个内项是2.5。
故答案为:2.5。
【名师点评】本题主要考查比例的基本性质,运用比例的基本性质是解答本题的关键。
26.【考点】比与分数、除法的关系.
【答案】见试题解答内容
【思路分析】把每个方格的边长看作“1”,则整个长方形的长是“5”,宽是“1”,根据长方形的面积计算公式“S=ab”即可求得整个图形的面积;阴影三角形的底是“3”,高是“1”,根据三角形的面积计算公式“S=ah÷2”即可求得涂色三角形的面积。长方形的面积是5×1=5,涂色三角形的面积是3×1÷2,涂色部分面积是整个图形面积的5。根据分数的基本性质,的分子、分母都乘5就是;根据比与分数的关系,3:10,再根据比的基本性质比的前、后项都乘3就是9:30;都乘12就是36:120;3÷10=0.3;把0.3的小数点向右移动两位添上百分号就是30%。
【解答】解:9:30=30%36:120=0.3。
故答案为:30,30,50,36,0.3。
【名师点评】此题主要是考查小数、分数、百分数、比之间的关系及转化。利用它们之间的关系和性质进行转化即可。求出涂色部分占整个图形的几分之几是关键。
三.计算题
27.【考点】分数的四则混合运算;分数的加法和减法;分数乘法;分数除法.
【答案】24,,9,,。
【思路分析】根据分数、小数加减乘除法的计算方法进行解答即可。
【解答】解:
24
9
【名师点评】此题考查了分数、小数加减乘除法的口算能力,注意认真计算即可。
28.【考点】百分数方程求解.
【答案】(1)x=2;(2)x=4;(3)x=6.75。
【思路分析】(1)首先化简,然后根据等式的性质,两边同时乘即可。
(2)首先根据比例的基本性质化简,然后根据等式的性质,两边同时乘即可。
(3)首先根据比例的基本性质化简,然后根据等式的性质,两边同时除以8即可。
【解答】解:(1)2x﹣30%x=3
x
x
x=2
(2):x:
x
x
x
x=4
(3)
8x=3.6×15
8x=54
8x÷8=54÷8
x=6.75
【名师点评】此题主要考查了根据等式的性质解方程的能力,即等式两边同时加上或同时减去、同时乘或同时除以一个数(0除外),两边仍相等。
29.【考点】分数的四则混合运算.
【答案】,,48。
【思路分析】(1)运用加法交换律、减法性质进行简算;
(2)从左向右进行计算;
(3)运用乘法分配律进行简算。
【解答】解:(1)
=()﹣()
1
(2)60%
(3)4.8×3.9+6.1×4
=4.8×3.9+6.1×4.8
=4.8×(3.9+6.1)
=4.8×10
=48
【名师点评】本题考查了四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
四.操作题
30.【考点】作旋转一定角度后的图形;图形的放大与缩小;作轴对称图形;作平移后的图形.
【答案】
【思路分析】①根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的右边画出图形A的关键对称点,连接即可。
②根据平移图形的特征,把图形B的6个顶点分别向右平移7格,再向下平移2格,首尾连接各点,即可得到图形B先向右平移7格,再向下平移2格后的图形B′。
③根据旋转的意义,找出图中图形C的4个关键点,再画出按顺时针方向旋转90度后的形状即可。
④按2:1的比例画出三角形D放大后的图形,就是把三角形的底和高分别放大2倍,原来三角形的底是3格、高2格,放大后图形的底是6格、高4格。
完成作图即可。
【解答】解:如图:
【名师点评】此题是考查作轴对称图形、作平移的图形、作旋转图形,关键是确定对称点(对应点)的位置。
五.应用题
31.【考点】关于圆锥的应用题;长方体和正方体的体积;圆锥的体积.
【答案】0.785米。
【思路分析】依据题意结合图示可知,利用圆锥的体积=π×底面半径×底面半径×高÷3,长方体的体积=长×宽×高,结合题中数据计算即可。
【解答】解:3.14×2×2×1.5÷3
=3.14×2
=6.28(立方米)
6.28÷4÷2=0.785(米)
答:可以铺0.785米。
【名师点评】本题考查的是圆锥、长方体的体积公式的应用。
32.【考点】长方形、正方形的面积.
【答案】120块。
【思路分析】根据正方形的面积公式:S=a2,求出每块方砖的面积,用每块方砖的面积乘需要的块数就是厨房地面的面积,然后根据“包含”除法的意义,用除法解答。
【解答】解:0.09平方米=9平方分米
2×2×270÷9
=4×270÷9
=1080÷9
=120(块)
答:需要120块。
【名师点评】此题主要考查正方形面积公式的灵活运用,关键是熟记公式。
33.【考点】圆柱的侧面积、表面积和体积.
【答案】150.72立方厘米。
【思路分析】根据题意可知,把这个圆柱的高减少后,即高减少了123(厘米),表面积减少的是高为3厘米的圆柱的侧面积,根据圆柱的侧面积公式:S=πdh,据此可以求出圆柱的底面直径,再根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:123(厘米)
37.68÷3÷3.14
=12.56÷3.14
=4(厘米)
3.14×(4÷2)2×12
=3.14×4×12
=12.56×12
=150.72(立方厘米)
答:原来圆柱的体积是150.72立方厘米。
【名师点评】此题主要考查圆柱的表面积公式、体积公式的灵活运用,关键是根据减少的高、减少的表面积求出圆柱的底面直径。
34.【考点】分数除法应用题.
【答案】6400千克。
【思路分析】把天舟一号货运飞船载货量看作单位“1”,用天舟六号货运飞船的载货量除以对应的分率,即可求出天舟一号货运飞船的载货能力。
【解答】解:74006400(千克)
答:天舟一号货运飞船的载货能力约是6400千克。
【名师点评】本题主要考查了分数除法应用题,解题的关键是明确:已知一个数的几分之几是多少,求这个数,用除法计算。
35.【考点】百分数的实际应用.
【答案】18件。
【思路分析】把六(2)班提交的作品数看作单位“1”,则六(1)班提交的作品数是1﹣25%,根据百分数乘法的意义解答即可。
【解答】解:24×(1﹣25%)
=24×0.75
=18(件)
答:六(1)班提交了18件作品。
【名师点评】本题考查的是百分数乘法的运用。
36.【考点】圆柱的侧面积、表面积和体积.
【答案】314立方厘米。
【思路分析】根据圆柱的体积(容积)公式:V=πr2h,把数据代入公式求出当水面高是12厘米时,水与石子的体积,然后减去原来水的体积就是乌鸦至少要衔石子的体积。
【解答】解:628毫升=628立方厘米
3.14×(10÷2)2×12﹣628
=3.14×25×12﹣628
=78.5×12﹣628
=942﹣628
=314(立方厘米)
答:乌鸦至少要衔314立方厘米的石子放进容器中才能喝到水。
【名师点评】此题主要考查圆柱的体积(容积)公式的灵活运用,关键是熟记公式,注意:体积单位与容积单位之间的换算。
21世纪教育网(www.21cnjy.com)
2025年秋六年级数学小升初开学名校分班摸底培优卷(北师大版)
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题
1.不能与组成比例的是( )
A.16:12 B.3:4 C.1: D.0.8:0.6
2.一个三角形有三个锐角,其中一个角是60°,这个三角形一定是( )
A.等边三角形 B.直角三角形 C.锐角三角形 D.无法确定
3.以下说法正确的是( )
A.人的近视度数和年龄成正比例。
B.A+B=100,那么A和B成反比例。
C.(M+2)x=y,且x和y都不为0,当M一定时,x和y不成比例。
D.圆锥的高一定,体积和底面积成正比例。
4.圆周率是圆的周长与直径的比值,公元263年,中国数学家刘徽用“割圆术”计算圆周率,公元480年左右,南北朝数学家祖冲之进一步得到圆周率小数点后7位的结果。如果如图中线段AF表示一个圆的周长,那么这个圆的直径可能是( )
A.线段AB B.线段AC C.线段AD D.线段CE
5.一个三角形有两个内角分别是50°和80°,它是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.无法确定
6.一个电子零件的实际长度是2毫米,画在图纸上的长度是8厘米,这张图纸的比例尺是( )
A.1:4 B.4:1 C.40:1 D.1:40
7.用2、5、8三张数字卡片摆三位数,这些三位数都是( )
A.2的倍数 B.3的倍数 C.5的倍数 D.以上答案都不对
8.张华用5cm、8cm和4cm的木棒首尾相接拼了一个三角形,李明也用同样的3根小棒,首尾相接拼了一个三角形,李明拼的三角形和张华的相比,( )
A.形状相同,大小相等 B.形状相同,大小不等
C.形状不同,大小不等 D.形状不同,大小相等
9.将0.75转换为分数,这些分数的分子和分母都是小于30的自然数,这样的分数共有( )个。
A.3 B.5 C.7 D.9
10.一个立体图形从上面看是,从左面看是,从前面看是,这个立体图形是( )
A. B. C. D.
11.下列各组数中,不能通过加、减,乘、除(含括号)运算得到24的是( )
A.1,1,7,7 B.2,2,8,8 C.1,1,2,8 D.1,1,4,6
12.如图四个图通过平移排成一横行,彼此之间没有空隙,正确的排列顺序是( )
A.③②①④ B.②①④③ C.①③④② D.④②①③
二.填空题
13.摄氏温度和华氏温度的关系是T℉=1.8t℃+32(t为摄氏温度数,T为华氏温度数)。如果一个人的体温是37℃,那么这个人的体温转化成华氏温度是 ℉。
14.根据世卫组织最新实时统计数据,截至欧洲中部夏令时间6月14日18时13分(北京时间6月15日0时13分),全球累计新冠肺炎确诊病例533816957例,533816957读作 ,改写成以“万”为单位的数是 万,四舍五入到亿位约是 亿。
15.如图中的7个点连在一起形成了两个完全一样的长方形,其中2个点的位置用数对表示分别是(1,5)、(5,1)请写出A点和B点的数对。
A点的数对是( , );B点的数对是( , )。
16.18的因数有 ,选出其中四个数组成一个比例是 。
17.一个圆柱的底面积是15cm2,高是8cm,这个圆柱的体积是 cm3。
18.把改写成乘法算式是 ,当a=123时,算式结果是 。
19.把一根圆柱形钢材切削成一个最大的圆锥,切削掉部分的体积为8dm3,这根圆柱形钢材的体积是______ dm3。
20.六(1)班师生46人去野营,一共租了10顶帐篷,正好住满。每顶大帐篷住5人,每顶小帐篷住3人。大帐篷有 顶,小帐篷有 顶。
21.如图,把左边的三角形按比例缩小后得到右边的三角形,则x= 。
22.如图,小朋友在玩“老狼捉小羊”的游戏。以老狼所在的位置为观测点,小羊A在老狼的 偏 , °方向上,小羊B在老狼的 偏 , °方向上。
23.盒子里装有三种除颜色外其它完全相同的球,黄色有9个,红色有5个,白色有2个,任意摸出一个球,摸出 色球的可能性最大。
24.将一条线段的一个端点不动,另一个端点旋转一周,其轨迹所形成的图形是 ;将一个半圆形沿着它的直径旋转一周,其轨迹所形成的图形是 。
25.在一个比例式里,两个外项互为倒数其中一个内项是0.4,那么另一个内项是 。
26.根据如图中涂色部分与整个图形的面积关系填写右边的等式。
9: = % :120= 填小数
三.计算题
27.直接写出得数。
28.解方程或比例。
2x﹣30%x=3
29.用你喜欢的方法计算。
四.操作题
30.按要求画图形。
(1)按给定的对称轴m,画出与图形A轴对称的图形,得到图形A′。
(2)画出图形B先向右平移7格,再向下平移2格后的图形B′。
(3)画出图形C绕O点顺时针旋转90度后得到的图形C′。
(4)按照2:1的比,画出图形D放大后的图形D′。
五.应用题
31.一个圆锥形的沙堆,底面半径是2米,高是1.5米,如果把这些沙子铺在长4米,宽2米的长方体沙坑内,可以铺多高?
32.淘气家装修厨房,原计划用边长2分米的方砖,需要270块。如果改用面积为0.09平方米的方砖铺,需要多少块呢?
33.一个圆柱体的高是12厘米,如果将这个圆柱体的高减少,那么它的表面积就减少37.68平方厘米,原来圆柱体的体积是多少立方厘米?
34.2023年5月10日,我国天舟六号“太空快递”发射成功。天舟六号货运飞船的载货能力达到了7400千克,约是天舟一号货运飞船载货能力的,天舟一号货运飞船的载货能力约是多少千克?
35.6月26日是国际禁毒日,阳光小学组织了以“珍爱生命拒绝毒品”为主题的绘画创作大赛,六(2)班提交了24件作品,六(1)班提交的作品比六(2)班少25%,六(1)班提交了多少件作品?
36.如图,圆柱体容器中有628毫升的水,乌鸦至少要衔多少立方厘米的石子放进容器中才能喝到水?
参考答案及试题解析
一.选择题
1.【考点】比例的意义和基本性质.
【答案】B
【思路分析】比例的基本概念,比值相等的两个比组成比例,算出各项的比值,据此判断即可。
【解答】解::
A.16:12
B.3:4
C.1:
D.0.8:0.6
:和3:4的比值不相等,所以不能组成比例。
故选:B。
【名师点评】此题需要学生熟练掌握比例的意义并灵活运用。
2.【考点】三角形的分类.
【答案】C
【思路分析】根据三角形的分类知识可知,三个角都是锐角的三角形是锐角三角形,据此解答即可。
【解答】解:三角形有三个锐角,其中一个角是60°,这个三角形一定是锐角三角形。
故选:C。
【名师点评】本题考查了三角形的分类知识,结合题意分析解答即可。
3.【考点】辨识成正比例的量与成反比例的量.
【答案】D
【思路分析】两种相关联的量,若两种量的比值一定,两种量成正比例;若两种量的乘积一定,两种量成反比例。
【解答】解:选项A中,人的近视度数和年龄不是相关联的量,人的近视度数和年龄不成比例。原题说法错误。
选项B中,A+B=100,A与B的和一定,A与B不成比例。原题说法错误。
选项C中,由(M+2)x=y,可得M+2,当M一定时,y和x的比值一定,y和x成正比例。原题说法错误。
选项D 中,圆锥的高=3×体积÷底面积,圆锥的高一定,体积和底面积的商一定,体积和底面积成正比例。原题说法正确。
故选:D。
【名师点评】辨识两种相关联的量成正比例还是成反比例,就看两种量的比值一定还是乘积一定。
4.【考点】圆的认识与圆周率.
【答案】D
【思路分析】根据圆周率的含义:圆的周长和它直径的比值,叫做圆周率,圆周率用π表示,根据圆的周长=直径乘π,即C=πd,直径为d,那么周长与直径的比值即是π。因为π的近似值是3.14,所以图中线段AF代表一个圆的周长的话,那么这个圆的直径大约是周长的三分之一,据此解答即可。
【解答】解:根据圆的周长=直径乘π,即C=πd,C÷d=π,π≈3.14,图中线段AF代表一个圆的周长,则圆的直径大约是周长的三分之一,根据图示线段CE最适合。
故选:D。
【名师点评】此题解答关键是明确π大约等于3.14,周长大约是直径的三倍。
5.【考点】三角形的内角和;等腰三角形与等边三角形.
【答案】A
【思路分析】先根据三角形内角和定理求出另一个角的度数,进而可得出结论。
【解答】解:因为一个三角形的两个内角分别是50°、80°,
所以此三角形另一个内角=180°﹣80°﹣50°=50°,
所以它是等腰三角形。
故选:A。
【名师点评】本题考查的是三角形内角和定理,熟知“三角形内角和是180°”是解答此题的关键。
6.【考点】比例尺.
【答案】C
【思路分析】根据比例尺的意义作答,即图上距离与实际距离的比。
【解答】解:2毫米=0.2厘米
8:0.2
=(8÷0.2):(0.2÷0.2)
=40:1
答:这张图纸的比例尺是40:1。
故选:C。
【名师点评】本题主要考查了比例尺的意义,注意图上距离与实际距离的单位要统一。
7.【考点】2、3、5的倍数特征.
【答案】B
【思路分析】个位上是0,2,4,6,8的数是2的倍数;个位上是0或5的数是5的倍数;如果一个数的各个数位上的数的和是3的倍数,那么这个数就是3的倍数。
【解答】解:2+5+8=15,15是3的倍数,所以这些三位数都是3的倍数。
故选:B。
【名师点评】熟练掌握2、3、5的倍数的特征是解决此题的关键。
8.【考点】三角形的特性.
【答案】A
【思路分析】根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边,因为三边都相等,所以围成的图形形状相同,大小也相等;由此解答即可。
【解答】解:因为4+5>8,所以能摆成三角形,且形状相同,大小相等。
故选:A。
【名师点评】本题考查了三角形的特性,注意任意两边之和大于第三边,任意两边之差小于第三边。
9.【考点】小数与分数的互化.
【答案】C
【思路分析】小数化成分数:原来有几位小数,就在1的后面写几个零作分母,把原来的小数去掉小数点作分子,能约分的要约分;再根据分数的基本性质即可求解。
【解答】解:0.75
30÷4=7......2
答:这样的分数共有7个。
故选:C。
【名师点评】本题考查了小数与分数的互化,关键是熟练掌握小数化成分数的方法。
10.【考点】从不同方向观察物体和几何体.
【答案】B
【思路分析】根据从上面、左面和前面看到的形状可知,该几何体由8个小正方体拼成,下层6个分两行,上面一行4个,下面一行2个,左右齐;上面一层2个,分别在下层后排左起第2个的上面和前排右面的上面。据此解答。
【解答】解:一个立体图形从上面看是,从左面看是,从前面看是,这个立体图形是。
故选:B。
【名师点评】本题是考查从不同方向观察物体和几何图形,关键是培养学生的观察能力。
11.【考点】带括号的表内除加、除减.
【答案】A
【思路分析】24点是4个数通过四则运算、括号得到24的一种数学游戏。分别尝试A、B、C、D中的数字,发现A中的数据不能通过加、减,乘、除(含括号)运算得到24。
【解答】解:A.1,1,7,7不能通过加、减,乘、除(含括号)运算得到24
B.(8﹣2)×(8÷2)=6×4=24
C.8×(2+1)÷1=8×3÷1=24
D.(4×1)×(6×1)=4×6=24
所以只有选项A不能通过加、减,乘、除(含括号)运算得到24。
故选:A。
【名师点评】本题考查填符号组算式。数通过四则运算、括号得到24即可。
12.【考点】平移.
【答案】D
【思路分析】根据图形连接点的特征排列即可。
【解答】解:四个图通过平移排成一横行,彼此之间没有空隙,正确的排列顺序是:④②①③。
故选:D。
【名师点评】本题主要考查了平移,解题的关键是观察图形的连接点。
二.填空题
13.【考点】含字母式子的求值.
【答案】98.6℉。
【思路分析】根据摄氏温度和华氏温度的关系是T℉=1.8t℃+32(t为摄氏温度数,T为华氏温度数),所以只要把一个量代入就可以求另外一个量。
【解答】解:已知一个人的体温是37℃,所以代入公式可得:
T℉=1.8×37℃+32
=66.6℃+32
=98.6℉
故答案为:98.6℉。
【名师点评】此题考查了摄氏温度和华氏温度关系的转换,只需代入公式计算就可以了。
14.【考点】亿以上数的改写与近似;亿以内数的改写与近似.
【答案】见试题解答内容
【思路分析】根据整数的读法,从高位起一级一积地往下读,读完亿级的数后面加一个“亿”字,读完万级里数后面加一个“万”字,再读个级里数;把一个数改写成用“万”作单位的数,在万万位是右下角点上小数点,后面写上万字,利用“四舍五入”法,熟练亿为后面尾数求近似数,根据千万位上数字的大小确定用“四舍”、还是用“五入”,据此解答即可。
【解答】解:533816957读作:五亿三千三百八十一万六千九百五十七;
533816957=53381.6957万
533816957≈5亿
故答案为:五亿三千三百八十一万六千九百五十七;53381.6957;5。
【名师点评】此题考查的目的是理解掌握整数的读法及应用,整数的改写方法、利用“四舍五入”省略亿位后面的尾数求近似数的方法及应用。
15.【考点】数对与位置.
【答案】5,3;9,1。
【思路分析】数对(1,5)表示的点取名为C点、数对(5,1)表示的点取名为D点;A点所在的行在C点和D点所在行的正中间,用C点和D点行数的和再除以2,可得A点的行数,A点所在的列与D点所在的列相同;B行所在的行与D点所在的行相同,B点所在列数比D点的列数多的值等于D点列数比C点列数多的值;据此解答即可。
【解答】解:数对(1,5)表示的点取名为C点、数对(5,1)表示的点取名为D点;
A点所在的列与D点所在的列相同,在第5列,
A点所在的行:(5+1)÷2=3,
A点用数对表示是(5,3);
B点所在列:5+(5﹣1)=9,
B点所在行与D点所在行相同,在第1行,
B点用数对表示是(9,1)。
故答案为:5,3;9,1。
【名师点评】本题考查数对知识点,用数对表示位置时,前面一个数表示列,后面一个数表示行。
16.【考点】比例的意义和基本性质.
【答案】见试题解答内容
【思路分析】一个数的因数的个数是有限的最小的是1,最大的是它本身;比例的意义是:表示两个比相等的式子叫作比例;由此解答。
【解答】解:18的因数有:1、2、3、6、9、18;
组成一个比例是:1:2=3:6(答案不唯一)。
故答案为:1、2、3、6、9、18;1:2=3:6(答案不唯一)。
【名师点评】此题主要根据求一个数的因数的方法和比例的意义解答。
17.【考点】圆柱的侧面积、表面积和体积.
【答案】120。
【思路分析】圆柱的体积公式V=Sh,据此代入数据计算即可。
【解答】解:15×8=120(立方厘米)
答:这个圆柱的体积是120cm3。
故答案为:120。
【名师点评】本题考查了圆柱体积公式的应用。
18.【考点】用字母表示数;含字母式子的求值.
【答案】见试题解答内容
【思路分析】表示a个相加的和是多少,即a;
当a=123时,代入a求出结果即可。
【解答】解:把改写成乘法算式是a,当a=123时,算式结果是41。
故答案为:a,41。
【名师点评】分数乘整数的意义,与整数乘法的意义相同,表示求几个相同加数的和是多少。
19.【考点】圆柱的侧面积、表面积和体积.
【答案】见试题解答内容
【思路分析】把一根圆柱形钢材切削成一个最大的圆锥,说明圆柱和圆锥等底等高,圆柱的体积是圆锥体积的3倍,削去部分的体积是圆锥体积的(3﹣1)倍,利用圆柱的体积除以2即可求出圆锥的体积,再利用圆锥的体积乘3即可。
【解答】解:8÷(3﹣1)
=8÷2
=4(立方分米)
4×3=12(立方分米)
答:这根圆柱形钢材的体积是12dm3。
故答案为:12。
【名师点评】本题考查了等底等高圆柱体积与圆锥体积之间的关系。
20.【考点】鸡兔同笼.
【答案】见试题解答内容
【思路分析】设10顶帐篷都是大帐篷,则一共可以住:10×5=50(人),这比实际的46人多50﹣46=4(人),又因为每顶大帐篷比小帐篷多住5﹣3=2(人),所以小帐篷有:4÷2=2(顶),进而求出大帐篷个数即可。
【解答】解:设10顶帐篷都是大帐篷。
小帐篷顶数:
(10×5﹣46)÷(5﹣3)
=4÷2
=2(顶)
大帐篷顶数:
10﹣2=8(顶)
所以大帐篷有8顶,小帐篷有2顶。
故答案为:8;2。
【名师点评】此题属于鸡兔同笼问题,解这类题的关键是用假设法进行分析,进而得出结论;也可以用方程进行解答。
21.【考点】图形的放大与缩小.
【答案】见试题解答内容
【思路分析】根据三角形的高的比可求出三角形缩小的比例,利用比例求出缩小后的底是多少即可。
【解答】解:3:4.8=1:1.6=5:8
说明三角形是按5:8进行缩小的,缩小后的底是原来三角形底的:
6.44
因此x等于4。
故答案为:4。
【名师点评】解答此题的关键是根据高的长度求出三角形的缩小比例。
22.【考点】根据方向和距离确定物体的位置.
【答案】见试题解答内容
【思路分析】在地图上按照“上北下南,左西右东”确定方向,注意观测点是老狼所在的位置。
【解答】解:小朋友在玩“老狼捉小羊”的游戏。以老狼所在的位置为观测点,小羊A在老狼的北偏西,45°方向上,小羊B在老狼的北偏东,45°方向上。
故答案为:北,西,45,北,东,45。
【名师点评】本题主要考查学生的方位感和对基本方向的辨别。
23.【考点】可能性的大小.
【答案】黄。
【思路分析】在这个盒子里面一共有三种颜色的球,黄色球的数量最多,白色球的数量最少,同种颜色多的球摸到的可能性大,同种颜色少的球摸到的可能性小。
【解答】解:盒子里装有三种除颜色外其它完全相同的球,黄色有9个,红色有5个,白色有2个,任意摸出一个球,摸出黄色球的可能性最大。
故答案为:黄。
【名师点评】本题考查可能性大小的判断,解题关键是理解并掌握影响可能性大小的因素,理解哪种颜色的球多,摸到哪种球的可能性就大。
24.【考点】圆的认识与圆周率.
【答案】圆,球。
【思路分析】一条线段的一个端点不动,另一个端点旋转一周,根据点动成线的原理即可理解。
一个半圆面围绕一条直径为轴旋转一周,根据面动成体的原理即可解。
【解答】解:将一条线段的一个端点不动,另一个端点旋转一周,其轨迹所形成的图形是圆;将一个半圆形沿着它的直径旋转一周,其轨迹所形成的图形是球。
故答案为:圆,球。
【名师点评】本题考查了点、线、面、体,平面图形旋转可以得到立体图形,体现了点动成线,面动成体的运动观点。
25.【考点】比例的意义和基本性质.
【答案】2.5。
【思路分析】两个外项互为倒数,则两外项之积是1,根据比例的基本性质“在比例中,两外项之积等于两内项之积”,可得两内项之积也等于1,据此计算即可。
【解答】解:1÷0.4=2.5
答:另一个内项是2.5。
故答案为:2.5。
【名师点评】本题主要考查比例的基本性质,运用比例的基本性质是解答本题的关键。
26.【考点】比与分数、除法的关系.
【答案】见试题解答内容
【思路分析】把每个方格的边长看作“1”,则整个长方形的长是“5”,宽是“1”,根据长方形的面积计算公式“S=ab”即可求得整个图形的面积;阴影三角形的底是“3”,高是“1”,根据三角形的面积计算公式“S=ah÷2”即可求得涂色三角形的面积。长方形的面积是5×1=5,涂色三角形的面积是3×1÷2,涂色部分面积是整个图形面积的5。根据分数的基本性质,的分子、分母都乘5就是;根据比与分数的关系,3:10,再根据比的基本性质比的前、后项都乘3就是9:30;都乘12就是36:120;3÷10=0.3;把0.3的小数点向右移动两位添上百分号就是30%。
【解答】解:9:30=30%36:120=0.3。
故答案为:30,30,50,36,0.3。
【名师点评】此题主要是考查小数、分数、百分数、比之间的关系及转化。利用它们之间的关系和性质进行转化即可。求出涂色部分占整个图形的几分之几是关键。
三.计算题
27.【考点】分数的四则混合运算;分数的加法和减法;分数乘法;分数除法.
【答案】24,,9,,。
【思路分析】根据分数、小数加减乘除法的计算方法进行解答即可。
【解答】解:
24
9
【名师点评】此题考查了分数、小数加减乘除法的口算能力,注意认真计算即可。
28.【考点】百分数方程求解.
【答案】(1)x=2;(2)x=4;(3)x=6.75。
【思路分析】(1)首先化简,然后根据等式的性质,两边同时乘即可。
(2)首先根据比例的基本性质化简,然后根据等式的性质,两边同时乘即可。
(3)首先根据比例的基本性质化简,然后根据等式的性质,两边同时除以8即可。
【解答】解:(1)2x﹣30%x=3
x
x
x=2
(2):x:
x
x
x
x=4
(3)
8x=3.6×15
8x=54
8x÷8=54÷8
x=6.75
【名师点评】此题主要考查了根据等式的性质解方程的能力,即等式两边同时加上或同时减去、同时乘或同时除以一个数(0除外),两边仍相等。
29.【考点】分数的四则混合运算.
【答案】,,48。
【思路分析】(1)运用加法交换律、减法性质进行简算;
(2)从左向右进行计算;
(3)运用乘法分配律进行简算。
【解答】解:(1)
=()﹣()
1
(2)60%
(3)4.8×3.9+6.1×4
=4.8×3.9+6.1×4.8
=4.8×(3.9+6.1)
=4.8×10
=48
【名师点评】本题考查了四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
四.操作题
30.【考点】作旋转一定角度后的图形;图形的放大与缩小;作轴对称图形;作平移后的图形.
【答案】
【思路分析】①根据轴对称图形的特征,对称点到对称轴的距离相等,对称点的连线垂直于对称轴,在对称轴的右边画出图形A的关键对称点,连接即可。
②根据平移图形的特征,把图形B的6个顶点分别向右平移7格,再向下平移2格,首尾连接各点,即可得到图形B先向右平移7格,再向下平移2格后的图形B′。
③根据旋转的意义,找出图中图形C的4个关键点,再画出按顺时针方向旋转90度后的形状即可。
④按2:1的比例画出三角形D放大后的图形,就是把三角形的底和高分别放大2倍,原来三角形的底是3格、高2格,放大后图形的底是6格、高4格。
完成作图即可。
【解答】解:如图:
【名师点评】此题是考查作轴对称图形、作平移的图形、作旋转图形,关键是确定对称点(对应点)的位置。
五.应用题
31.【考点】关于圆锥的应用题;长方体和正方体的体积;圆锥的体积.
【答案】0.785米。
【思路分析】依据题意结合图示可知,利用圆锥的体积=π×底面半径×底面半径×高÷3,长方体的体积=长×宽×高,结合题中数据计算即可。
【解答】解:3.14×2×2×1.5÷3
=3.14×2
=6.28(立方米)
6.28÷4÷2=0.785(米)
答:可以铺0.785米。
【名师点评】本题考查的是圆锥、长方体的体积公式的应用。
32.【考点】长方形、正方形的面积.
【答案】120块。
【思路分析】根据正方形的面积公式:S=a2,求出每块方砖的面积,用每块方砖的面积乘需要的块数就是厨房地面的面积,然后根据“包含”除法的意义,用除法解答。
【解答】解:0.09平方米=9平方分米
2×2×270÷9
=4×270÷9
=1080÷9
=120(块)
答:需要120块。
【名师点评】此题主要考查正方形面积公式的灵活运用,关键是熟记公式。
33.【考点】圆柱的侧面积、表面积和体积.
【答案】150.72立方厘米。
【思路分析】根据题意可知,把这个圆柱的高减少后,即高减少了123(厘米),表面积减少的是高为3厘米的圆柱的侧面积,根据圆柱的侧面积公式:S=πdh,据此可以求出圆柱的底面直径,再根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:123(厘米)
37.68÷3÷3.14
=12.56÷3.14
=4(厘米)
3.14×(4÷2)2×12
=3.14×4×12
=12.56×12
=150.72(立方厘米)
答:原来圆柱的体积是150.72立方厘米。
【名师点评】此题主要考查圆柱的表面积公式、体积公式的灵活运用,关键是根据减少的高、减少的表面积求出圆柱的底面直径。
34.【考点】分数除法应用题.
【答案】6400千克。
【思路分析】把天舟一号货运飞船载货量看作单位“1”,用天舟六号货运飞船的载货量除以对应的分率,即可求出天舟一号货运飞船的载货能力。
【解答】解:74006400(千克)
答:天舟一号货运飞船的载货能力约是6400千克。
【名师点评】本题主要考查了分数除法应用题,解题的关键是明确:已知一个数的几分之几是多少,求这个数,用除法计算。
35.【考点】百分数的实际应用.
【答案】18件。
【思路分析】把六(2)班提交的作品数看作单位“1”,则六(1)班提交的作品数是1﹣25%,根据百分数乘法的意义解答即可。
【解答】解:24×(1﹣25%)
=24×0.75
=18(件)
答:六(1)班提交了18件作品。
【名师点评】本题考查的是百分数乘法的运用。
36.【考点】圆柱的侧面积、表面积和体积.
【答案】314立方厘米。
【思路分析】根据圆柱的体积(容积)公式:V=πr2h,把数据代入公式求出当水面高是12厘米时,水与石子的体积,然后减去原来水的体积就是乌鸦至少要衔石子的体积。
【解答】解:628毫升=628立方厘米
3.14×(10÷2)2×12﹣628
=3.14×25×12﹣628
=78.5×12﹣628
=942﹣628
=314(立方厘米)
答:乌鸦至少要衔314立方厘米的石子放进容器中才能喝到水。
【名师点评】此题主要考查圆柱的体积(容积)公式的灵活运用,关键是熟记公式,注意:体积单位与容积单位之间的换算。
21世纪教育网(www.21cnjy.com)
同课章节目录
