(小升初开学分班考)小升初开学名校分班摸底押题卷-2025年秋六年级数学苏教版(含答案解析)
文档属性
| 名称 | (小升初开学分班考)小升初开学名校分班摸底押题卷-2025年秋六年级数学苏教版(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 277.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-16 10:42:21 | ||
图片预览




文档简介
/ 让学习更有效 小升初备考 | 数学学科
2025年秋六年级数学小升初开学名校分班摸底押题卷(苏教版)
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.计算题
1.直接写出得数。
3a×7a= 0.8﹣0.37=
0.32﹣0.22= 100÷20%= 0.7×9÷0.7×9=
2.用竖式计算,带*的要验算。
*50.1﹣14.62= 8.5×1.06= 0.798÷4.2=
3.计算下面各题,能简算的要简算。
7.5﹣1.26﹣4.74+2.5 6.8÷(0.5+0.3×4)
3.6×111+888×0.8
二.填空题
4.如图,两个涂色正方形的周长和是60厘米,大正方形的面积是 平方厘米。
5.港珠澳大桥是一座链接珠海和香港、澳门的桥隧工程,全长55千米,在一幅地图上,它的长度是11厘米,这幅地图的比例尺是 。
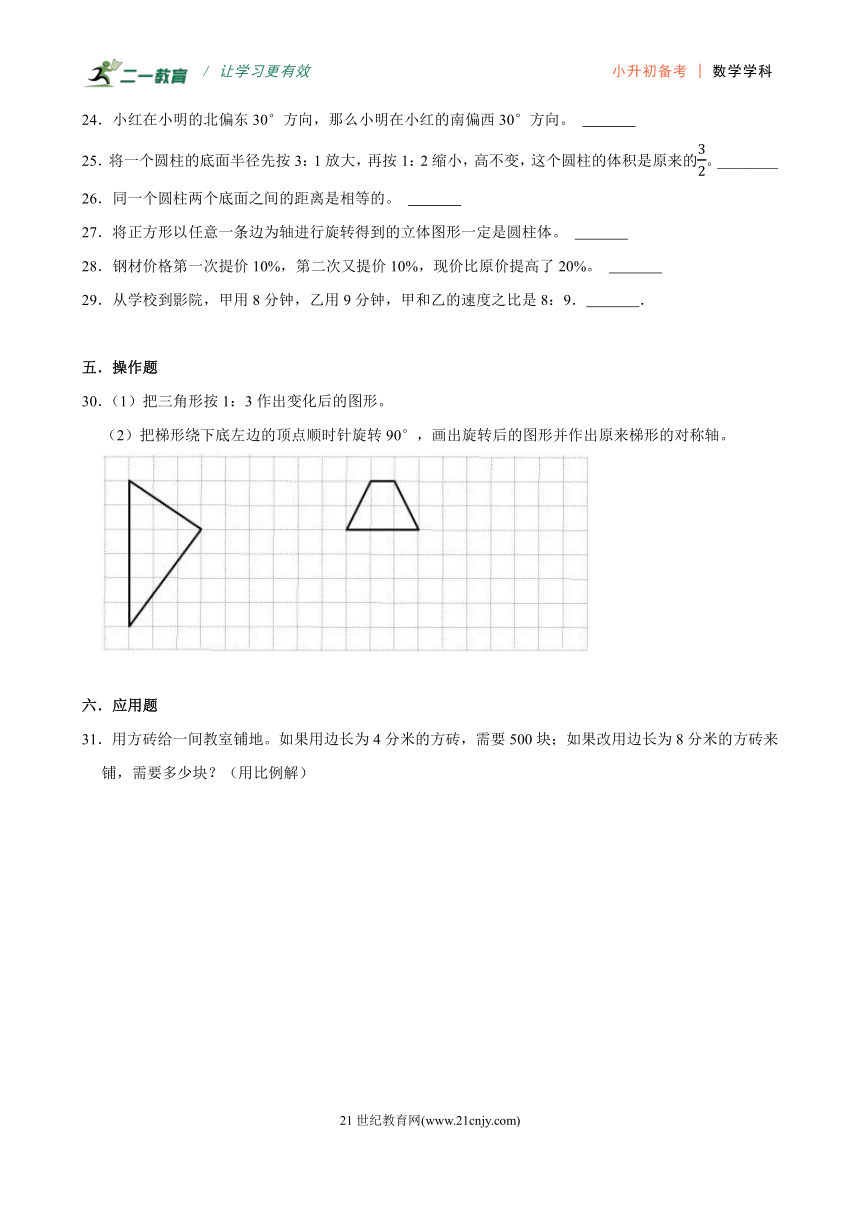
6.数学家阿基米德用“圆柱容球”实验(如图),发现了球的表面积正好是圆柱表面积的,如果圆柱的底面半径为3分米,那么球的表面积是 平方分米。
7.用五个长3厘米宽2厘米的长方形不重叠拼成一个更大的长方形,这个长方形的周长最小是_____ 厘米。
8.找规律填空:0.5,,37.5%,,, (填分数), (填百分数)。
9.在一个直径为8厘米的圆中画一个最大的正方形,这个正方形的面积是 平方厘米。
10.10.5cm3= L 2小时45分= 小时
11.“摄氏度”和“华氏度”都是用来计量温度的单位,它们之间的换算关系是“华氏度=32+摄氏度×1.8”。如果某人的体温是101.48华氏度,那么也就是 摄氏度。
12.从甲地到乙地,小明走了12分钟,小刚走了15分钟,小明和小刚的速度比是 .
13.如图是某圆柱形饮料瓶的规格尺寸,把12瓶这样的饮料装入纸盒中(紧密放置,如图)。这个纸盒的容积大约是 立方厘米。
14.现准备了一些边长为4厘米的正方形纸片,按如图方式摆放,每个重叠部分都是边长1厘米的小正方形,照这样摆下去,当用K张纸片时,摆成的图像面积是 平方厘米,周长是 厘米。
15.如图,把一个直径是4厘米的圆柱的底面平均分成若干个扇形,切开拼成一个近似的长方体,这个长方体前面的面积是210平方厘米,圆柱的体积是 立方厘米。
16.某次数学竞赛共20道题,评分标准是:每做对一题得5分,每做错或不做一题扣1分。小华参加了这次竞赛,得了64分。小华做对 道题。
三.选择题
17.六(1)班有学生50人,6月7日有2人请事假,1人请病假。六(1)班学生这天的出勤率是( )
A.94% B.95% C.96% D.98%
18.旋转转盘的指针,如果指针箭头停在奇数的位置,就能得到奖品。小苗第一次旋转的结果如图所示,她得奖了。如果再旋转一次,那么这次她( )
A.一定能得奖 B.不可能得奖 C.得奖可能性大 D.得奖可能性小
19.小明坐在教室的位置用数对(2,5)表示,小乐坐在小明的正后方,小乐的位置可能是( )
A.(3,5) B.(2,4) C.(1,5) D.(2,6)
20.把一个圆柱形木料削去24立方厘米,得到一个最大的圆锥,圆锥的体积是( )
A.12立方厘米 B.24立方厘米 C.36立方厘米 D.48立方厘米
21.把一个梯形的上底向一个方向延长2分米就变成了一个底是5分米、高是4分米的平行四边形。原来梯形的面积是( )平方分米。
A.20 B.10 C.16 D.32
22.用几个1立方厘米的正方体木块摆了一个物体,如图所示是从不同方向看到的图形,这个物体的体积是( )立方厘米。
A.5 B.6 C.7 D.8
23.1张餐桌可以坐6人,2张餐桌拼在一起可坐10人,如此拼下去,n张餐桌拼在一起可以坐( )人。
A.4n B.4+2n C.2+3n D.2+4n
四.判断题
24.小红在小明的北偏东30°方向,那么小明在小红的南偏西30°方向。
25.将一个圆柱的底面半径先按3:1放大,再按1:2缩小,高不变,这个圆柱的体积是原来的。________
26.同一个圆柱两个底面之间的距离是相等的。
27.将正方形以任意一条边为轴进行旋转得到的立体图形一定是圆柱体。
28.钢材价格第一次提价10%,第二次又提价10%,现价比原价提高了20%。
29.从学校到影院,甲用8分钟,乙用9分钟,甲和乙的速度之比是8:9. .
五.操作题
30.(1)把三角形按1:3作出变化后的图形。
(2)把梯形绕下底左边的顶点顺时针旋转90°,画出旋转后的图形并作出原来梯形的对称轴。
六.应用题
31.用方砖给一间教室铺地。如果用边长为4分米的方砖,需要500块;如果改用边长为8分米的方砖来铺,需要多少块?(用比例解)
32.亮亮看一本故事书,第一天看了全书的,第二天看了全书的,还剩160页没看。
(1)两天一共看了这本书的几分之几?
(2)这本书一共有多少页?
33.修一条800米的路,第一天修了全长的,第二天修了全长的。第二天修了多少米?还剩下多少米没修?
34.在一幅比例尺是1:5000000的地图上,量得甲、乙两地的图上距离是24厘米,一架飞机以800千米/时的速度从甲地飞往乙地,需要多少小时?
35.小强对他们班同学家里有电脑情况作了一个调查,发现他们家里有电脑的有18人,没有电脑的有20人,你能算出小强班上同学家的电脑普及率是多少吗?
36.周大伯把一块长为30米、宽为20米的长方形菜地分成两部分,分别种植黄瓜和番茄。种黄瓜的面积比种番茄的面积少180平方米,黄瓜和番茄各种了多少平方米?小明在思考这一题时,画出了两种不同图形:
(1)根据题意,将两幅图补充完整。
(2)列式解答:
参考答案及试题解析
一.计算题
1.【答案】;21a2;0.43;;;0.05;500;81。
【思路分析】根据分数、小数、百分数加减乘除法的计算方法以及四则混合运算的顺序,直接进行口算即可。
【解答】解:
3a×7a=21a2 0.8﹣0.37=0.43
0.32﹣0.22=0.05 100÷20%=500 0.7×9÷0.7×9=81
【名师点评】本题考查了简单的计算,计算时要细心,注意平时积累经验,提高计算的水平。
2.【答案】35.38,9.01,0.19。
【思路分析】计算小数减法:先把各数的小数点对齐(也就是把相同数位上的数对齐);再按照整数减法的法则进行计算,得数里的小数点要和横线上的小数点对齐(得数的小数部分末尾有0,一般要把0去掉)。
小数乘法法则:先把被乘数和乘数都看作整数,按照整数的乘法法则进行计算,求出整数乘法的积,然后,再看被乘数和乘数一共有几位小数,就从积的右边起数出几位,点上小数点。如果小数的末尾出现0时,根据小数的基本性质,要把它去掉。
小数除法法则:先移动除数的小数点,使它变成整数。除数的小数点向右移动几位,被除数的小数点也向右移动相同的位数(位数不够的补“0”),然后按照除数是整数的除法进行计算。
减法用差+减数=被减数进行验算。
【解答】解:50﹣14.62=35.38
8.5×1.06=9.01
0.798÷4.2=0.19
【名师点评】本题主要考查了小数减法、小数乘法、小数除法的竖式计算方法以及减法的验算方法,注意计算的准确性。
3.【答案】4,4,1110,。
【思路分析】(1)根据加法交换律和加法结合律,以及减法的性质计算;
(2)先算小括号里面的乘法,再算小括号里面的加法,最后算括号外的除法;
(3)先根据积不变规律变形,再根据乘法分配律简算;
(4)先算小括号里面的减法,再算中括号里面的除法,最后算括号外的乘法。
【解答】解:(1)7.5﹣1.26﹣4.74+2.5
=(7.5+2.5)﹣(1.26+4.74)
=10﹣6
=4
(2)6.8÷(0.5+0.3×4)
=6.8÷(0.5+1.2)
=6.8÷1.7
=4
(3)3.6×111+888×0.8
=3.6×111+111×6.4
=111×(3.6+6.4)
=111×10
=1110
(4)
[]
【名师点评】本题考查了四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
二.填空题
4.【答案】225。
【思路分析】通过观察图形可知,两个涂色正方形的周长和等于大正方形的周长,用周长除以4求出大正方形的边长,然后根据正方形的面积=边长×边长,把数据代入公式解答。
【解答】解:60÷4=15(厘米)
15×15=225(平方厘米)
答:大正方形的面积是225平方厘米。
故答案为:225。
【名师点评】此题主要考查正方形的周长公式、面积公式的灵活运用,关键是熟记公式。
5.【答案】1:500000。
【思路分析】根据比例尺的意义作答,即比例尺是图上距离与实际距离的比。
【解答】解:11厘米:55千米
=11厘米:5500000厘米
=1:500000
答:这幅地图的比例尺是1:500000。
故答案为:1:500000。
【名师点评】本题主要考查了比例尺的意义,注意图上距离与实际距离的单位要统一。
6.【答案】113.04。
【思路分析】依据题意可知,利用圆柱的表面积=π×底面半径×底面半径×2+π×底面半径×2×高,然后计算求的表面积。
【解答】解:3.14×3×3×2+3.14×3×2×6
=56.52+113.04
=169.56(平方分米)
169.56113.04(平方分米)
答:球的表面积是113.04平方分米。
故答案为:113.04。
【名师点评】本题考查的是圆柱表面积公式的应用。
7.【答案】见试题解答内容
【思路分析】如图所示,有3种拼法,分别求出的长方形的长和宽,进而利用长方形的周长周长=(长+宽)×2即可求解。
【解答】解:(1)(2×5+3)×2
=13×2
=26(厘米)
(2)(3×5+2)×2
=17×2
=34(厘米)
(3)(3×2+3+2)×2
=11×2
=22(厘米)
22<26<34
答:这个长方形的周长最小是22厘米。
故答案为:22。
【名师点评】此题主要考查长方形的周长的计算方法,关键是求出长方形的长和宽的值。
8.【答案】,35%。
【思路分析】把小数和百分数化成分数,观察题中分数可知,分子分别是1、2、3、4、5,后面一个数比前一个数大1,分母分别是2、5、8、11、14,后一个数比前一个数大3,由此解答本题。
【解答】解:由分析可知:5+1=6,14+3=17,这个分数是;
6+1=7,17+3=20,这个分数是0.35=35%。
故答案为:,35%。
【名师点评】解决本题的关键是找出题中的规律,利用规律去解答。
9.【答案】32。
【思路分析】根据圆内最大正方形的特征可知,这个正方形的对角线的长度等于圆的直径,把这个正方形看作两个完全一样的三角形,根据三角形的面积公式:S=ah÷2,把数据代入公式解答。
【解答】解:8×(8÷2)÷2×2
=8×4÷2×2
=32÷2×2
=32(平方厘米)
答:这个正方形的面积是32平方厘米。
故答案为:32。
【名师点评】此题考查的目的是理解掌握圆内最大正方形的特征及应用,三角形的面积公式、正方形的面积公式及应用。
10.【答案】0.0105,2.75。
【思路分析】低级单位立方厘米化高级单位升除以进率1000。
把45分除以进率60化成0.75小时再加2小时。
【解答】解:10.5cm3=0.0105L
2小时45分=2.75小时
故答案为:0.0105,2.75。
【名师点评】此题考查了体积(容积)的单位换算、时间的单位换算。单位换算首先要弄清是由高级单位化低级单位还是由低级单位化高级单位,其次记住单位间的进率。
11.【答案】38.6。
【思路分析】根据逆运算的方法可知摄氏度=(华氏度﹣32)÷1.8,代入数值进行计算即可。
【解答】解:(101.48﹣32)÷1.8
=69.48÷1.8
=38.6(摄氏度)
也就是38.6摄氏度。
故答案为:38.6。
【名师点评】本题考查小数四则混合运算的计算及应用。理解题意,找出数量关系,列式计算即可。
12.【答案】见试题解答内容
【思路分析】把甲地到乙地的路程看作单位“1”,根据“路程÷时间=速度”分别求出小明的速度和小刚的速度,进而根据题意求比即可.
【解答】解:(1÷12):(1÷15),
:,
=5:4;
故答案为:5:4.
【名师点评】解答此题用到的知识点:(1)比的意义;(2)路程、时间和速度三者之间的关系.
13.【答案】4320。
【思路分析】通过观察图形可知,这个盒子的长等于圆柱底面直径的6倍,盒子的宽等于圆柱底面直径的2倍,盒子的高等于圆柱的高,根据长方体的容积(体积)公式:V=abh,把数据代入公式解答。
【解答】解:(6×6)×(6×2)×10
=36×12×10
=432×10
=4320(立方厘米)
答:这个纸盒的容积是4320立方厘米。
故答案为:4320。
【名师点评】此题主要考查长方体的容积(体积)公式的灵活运用,关键是熟记公式。
14.【答案】(15K+1),(12K+4)。
【思路分析】用1个边长是4厘米正方形面积乘正方形的张数K再减去(K﹣1)×(1×1)平方厘米就得图形面积;用边长是4厘米的正方形周长乘K减去(K﹣1)×(1×4)厘米,就得图像的周长。
【解答】解:4×4×K﹣(K﹣1)×(1×1)
=16K﹣K+1
=(15K+1)平方厘米
4×4×K﹣(K﹣1)×(1×4)
=16K﹣4K+4
=(12K+4)厘米
故答案为:(15K+1),(12K+4)。
【名师点评】仔细观察,找到规律是解决本题的关键。
15.【答案】420。
【思路分析】长方体前面的面积是210平方厘米,即πrh=210平方厘米,圆柱体积=πr2h,据此求出圆柱的体积。
【解答】解:210×(4÷2)
=210×2
=420(立方厘米)
答:圆柱的体积是420立方厘米。
故答案为:420。
【名师点评】理解题目中长方体是如何由圆柱切开拼成的是解答的关键。
16.【答案】14。
【思路分析】由题意可知,每做错或不做一题要丢(5+1)分。假设小华全做对,可得20×5即100分,实际得了64分,丢了(100﹣64)分;用丢的(100﹣64)分除以(5+1)就是做错或没做的题数,最后用20减去做错或没做的题数就是做对的题数。
【解答】解:假设小华全做对。
(20×5﹣64)÷(5+1)
=36÷6
=6
20﹣6=14(道)
答:小华做对了14道。
故答案为:14。
【名师点评】本题属于鸡兔同笼问题,可以用假设法解答,也可以列方程解答。
三.选择题
17.【答案】A
【思路分析】先用“50﹣1﹣2”求出出勤人数,理解出勤率,即出勤的学生人数占全班总人数的百分之几,计算公式:出勤率100%;代入数值,解答即可。
【解答】解:100%=94%
答:六(1)班学生这天的出勤率是94%。
故选:A。
【名师点评】此题属于百分率问题,最大为100%,计算方法为一部分量(或全部量)除以全部量乘百分之百。
18.【答案】D
【思路分析】根据事件发生的可能性大小,哪种情况发生的数量最多,事件发生的可能性就最大;哪种情况发生的数量最少,事件发生的可能性就最小;哪种情况发生的数量一样多,事件发生的可能性就相等,据此分析即可解答。
【解答】解:根据题意可知:第一次旋转,指针箭头停在奇数的位置,得到奖品,剩余3个数都是偶数,所以她得奖的可能性小。
故选:D。
【名师点评】此题考查可能性的大小。掌握判断方法是解答的关键。
19.【答案】D
【思路分析】用数对表示位置时,先表示第几列,再表示第几行,小明坐在教室的位置用数对(2,5)表示,小乐坐在小明的正后方,列不变,行数增加,解答即可。
【解答】解:小明坐在教室的位置用数对(2,5)表示,小乐坐在小明的正后方,小乐的位置可能是(2,6)。
故选:D。
【名师点评】本题考查数对表示位置知识,结合题意分析解答即可。
20.【答案】A
【思路分析】把圆柱形状的木头削成最大的圆锥和原来的圆柱是等底等高的,根据等底等高圆柱体积是圆锥的体积的3倍,可知削去的部分为圆锥的2倍,据此即可解答。
【解答】解:24÷2=12(立方厘米)
答:圆锥的体积是12立方厘米。
故选:A。
【名师点评】此题考查了等底等高的圆锥和圆柱的体积关系。
21.【答案】C
【思路分析】这个梯形的上底是5﹣2=3(分米),下底是5分米,高是4分米,然后根据梯形的面积公式计算即可。
【解答】解:5﹣2=3(分米)
(3+5)×4÷2
=8×4÷2
=32÷2
=16(平方分米)
答:原来梯形的面积是16平方分米。
故选:C。
【名师点评】解答此题的关键是求出原来的梯形的上底的长度。
22.【答案】A
【思路分析】根据从前面和上面观察到的形状可知,该几何体由5个小正方体拼成,据此计算物体的体积即可。
【解答】解:4+1=5(个)
5×1=5(立方厘米)
答:这个物体的体积是5立方厘米。
故选:A。
【名师点评】本题是考查从不同方向观察物体和几何体,关键是培养学生的观察能力。
23.【答案】D
【思路分析】依据题意结合图示可知,1张餐桌可以坐6人,2张餐桌拼在一起可坐(6+4)人,3张餐桌拼在一起可坐(6+4+4)人,4张餐桌拼在一起可坐(6+4+4+4)人,n张餐桌拼在一起可坐[6+4×(n﹣1)]人,由此解答本题。
【解答】解:由分析可知:6+4×(n﹣1)=2+4n(人)
故选:D。
【名师点评】解决本题的关键是找出题中的规律,利用规律去解答。
四.判断题
24.【答案】√
【思路分析】根据位置的相对性可知,描述两个物体之间的相对位置时,方向相反,角度相等,或者先以小明为中心点,找到小红的位置后,再以小红为中心点找小明的位置,从而确定方向,据此解答。
【解答】解:通过分析可知,小红家在小明的北偏东30°方向,那么小明在小红的南偏西30°方向。画图如下:
原题说法正确。
故答案为:√。
【名师点评】本题考查了方向的认识,结合方向的相对性解答即可。
25.【答案】见试题解答内容
【思路分析】把原来圆的半径看作“1”,按3:1放大后的半径是(1×3),再按1:2缩小后的半径是(1×3)。根据圆柱的体积=底面积×高,分别求出原来圆柱的体积和现在的体积,再用现在的体积除以原来圆柱的体积,看结果是不是,如果是原题就正确,否则就错误。
【解答】解:设原来圆的半径看作“1”,按3:1放大后的半径是(1×3),再按1:2缩小后的半径是(1×3),高是h。
π×(1×3)×(1×3)h÷(π×1×1×h)
1
答:这个圆柱的体积是原来的。所以原题说法错误。
故答案为:×。
【名师点评】此题考查的知识点:图形放大与缩小的意义、圆柱体积的计算、分数除法的意义。
26.【答案】√
【思路分析】圆柱的两个底面之间的距离叫做高,圆柱的高相等。
【解答】解:同一个圆柱两个底面之间的距离是相等的。
故原题说法正确。
故答案为:√。
【名师点评】此题考查了圆柱的特征,要熟练掌握。
27.【答案】√
【思路分析】根据圆柱的侧面展开图的特征可知:正方形以任意一条边为轴,旋转一周得到的图形是圆柱,据此即可判断。
【解答】解:根据圆柱体的特征,将正方形以任意一条边为轴进行旋转得到的立体图形一定是圆柱体。这种说法是正确的。
故答案为:√。
【名师点评】根据圆柱的展开图,得出正方形旋转一周得到的是一个圆柱体。
28.【答案】×
【思路分析】先把原件看成单位“1”,第一次提价后的价格是原价的(1+10%),再把第一次提价后的价格看成单位“1”,根据分数乘法的意义,第二次提价后的价格是原价的(1+10%)×(1+10%),进而求出比原价高了百分之几,再与20%比较即可判断。
【解答】解:(1+10%)×(1+10%)
=110%×110%
=121%,
121%﹣1=21%,比原价提高了21%,不是20%。
答:原题干错误。
故答案为:×。
【名师点评】本题的关键是把单位“1”统一到原价上,求出现价比原价高百分之几,再比较。
29.【答案】见试题解答内容
【思路分析】根据题意,把从学校走到公园的路程看作单位“1”,可知甲、乙的速度分别是、,然后化简比即可.
【解答】解::9:8
答:甲和乙的速度比为9:8.
故答案为:×.
【名师点评】此题关键先求出两人的速度,再化简比.
五.操作题
30.【答案】(1)、(2)
【思路分析】(1)三角形看作底为6格,高为3格的三角形,根据图形缩小的意义,把这个三角形对应的底、高均缩小到原来的,对应角大小不变,所得到的图形就是原图形按1:3缩小后的图形。
(2)根据旋转的特征,梯形绕下底左边的顶点顺时针旋转90°,此顶点的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。旋转后的图形仍为等腰梯形,是轴对称图形,只有1条对称轴,即过上、下底中点的直线。
【解答】解:(1)、(2)画图如下:
【名师点评】此题考查了图形的放大与缩小、作旋转一定度数后的图形、确定轴对称图形对称轴的条数及位置。
六.应用题
31.【答案】125块。
【思路分析】根据题意可知:每块方砖的面积和所需的块数成反比例。据此设需要x块砖,然后列出方程即可求解。
【解答】解:设需要x块。
8×8×x=4×4×500
64x=8000
x=125
答:需要125块。
【名师点评】解答此题的关键是判断出方砖的块数与方砖的面积成反比例,注意题中的4分米与5分米是方砖的边长不是方砖的面积。
32.【答案】(1);
(2)700页。
【思路分析】(1)把这本故事书的页看作单位“1”,根据加法的意义,用加法解答。
(2)把这本故事书的页看作单位“1”,剩下没有看的页占这本故事书的(1),根据已知一个数的几分之几是多少,求这个数,用除法解答。
【解答】解:(1)
答:两天一共看了这本书的。
(2)160÷(1)
=160÷(1)
=160
=160
=700(页)
答:这本书一共有700页。
【名师点评】此题考查的目的是理解分数加法、分数除法的意义,掌握分数加法、分数除法的计算法则及应用。
33.【答案】320米;240米。
【思路分析】第二天修的长度=全长,剩下的长度=总长×(1﹣第一天修了全长的几分之几﹣第二天修了全长的几分之几),由此列式计算即可。
【解答】解:(米)
(米)
答:第二天修了320米,还剩240米没修。
【名师点评】解决本题的关键是找出题中数量关系。
34.【答案】1.5小时。
【思路分析】根据实际距离=图上距离÷比例尺,先求出甲、乙两地实际距离,再根据时间=路程÷速度,列式解答即可。
【解答】解:(厘米)
120000000厘米=1200千米
1200÷800=1.5(小时)
答:需要1.5小时。
【名师点评】熟练掌握比例尺公式,是解答此题的关键。
35.【答案】47.4%。
【思路分析】电脑的普及率=家里有电脑同学人数÷班级总人数×100%,班级总人数=家里有电脑同学人数+没有电脑的同学人数,据此列式计算即可。
【解答】解:18÷(18+20)×100%
=18÷38×100%
≈47.4%
答:小强班上同学家的电脑普及率约是47.4%。
【名师点评】本题主要考查百分率在生活中的应用。
36.【答案】黄瓜种了210平方米,番茄种了390平方米。
【思路分析】(1)根据小明未完成的图示继续补全图片;
(2)根据“长方形面积=长×宽”计算出长方形菜地的面积,即种植黄瓜和番茄的面积之和,根据和差公式“较大数=(和+差)÷2”求出番茄种植面积,用种植黄瓜和番茄的面积之和减去番茄种植面积即是黄瓜种植面积。
【解答】解:(1)如下图所示:
(2)30×20=600(平方米)
(600+180)÷2=390(平方米)
600﹣390=210(平方米)
答:黄瓜种了210平方米,番茄种了390平方米。
【名师点评】本题考查了和差公式的应用以及长方形面积的计算。
21世纪教育网(www.21cnjy.com)
2025年秋六年级数学小升初开学名校分班摸底押题卷(苏教版)
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.计算题
1.直接写出得数。
3a×7a= 0.8﹣0.37=
0.32﹣0.22= 100÷20%= 0.7×9÷0.7×9=
2.用竖式计算,带*的要验算。
*50.1﹣14.62= 8.5×1.06= 0.798÷4.2=
3.计算下面各题,能简算的要简算。
7.5﹣1.26﹣4.74+2.5 6.8÷(0.5+0.3×4)
3.6×111+888×0.8
二.填空题
4.如图,两个涂色正方形的周长和是60厘米,大正方形的面积是 平方厘米。
5.港珠澳大桥是一座链接珠海和香港、澳门的桥隧工程,全长55千米,在一幅地图上,它的长度是11厘米,这幅地图的比例尺是 。
6.数学家阿基米德用“圆柱容球”实验(如图),发现了球的表面积正好是圆柱表面积的,如果圆柱的底面半径为3分米,那么球的表面积是 平方分米。
7.用五个长3厘米宽2厘米的长方形不重叠拼成一个更大的长方形,这个长方形的周长最小是_____ 厘米。
8.找规律填空:0.5,,37.5%,,, (填分数), (填百分数)。
9.在一个直径为8厘米的圆中画一个最大的正方形,这个正方形的面积是 平方厘米。
10.10.5cm3= L 2小时45分= 小时
11.“摄氏度”和“华氏度”都是用来计量温度的单位,它们之间的换算关系是“华氏度=32+摄氏度×1.8”。如果某人的体温是101.48华氏度,那么也就是 摄氏度。
12.从甲地到乙地,小明走了12分钟,小刚走了15分钟,小明和小刚的速度比是 .
13.如图是某圆柱形饮料瓶的规格尺寸,把12瓶这样的饮料装入纸盒中(紧密放置,如图)。这个纸盒的容积大约是 立方厘米。
14.现准备了一些边长为4厘米的正方形纸片,按如图方式摆放,每个重叠部分都是边长1厘米的小正方形,照这样摆下去,当用K张纸片时,摆成的图像面积是 平方厘米,周长是 厘米。
15.如图,把一个直径是4厘米的圆柱的底面平均分成若干个扇形,切开拼成一个近似的长方体,这个长方体前面的面积是210平方厘米,圆柱的体积是 立方厘米。
16.某次数学竞赛共20道题,评分标准是:每做对一题得5分,每做错或不做一题扣1分。小华参加了这次竞赛,得了64分。小华做对 道题。
三.选择题
17.六(1)班有学生50人,6月7日有2人请事假,1人请病假。六(1)班学生这天的出勤率是( )
A.94% B.95% C.96% D.98%
18.旋转转盘的指针,如果指针箭头停在奇数的位置,就能得到奖品。小苗第一次旋转的结果如图所示,她得奖了。如果再旋转一次,那么这次她( )
A.一定能得奖 B.不可能得奖 C.得奖可能性大 D.得奖可能性小
19.小明坐在教室的位置用数对(2,5)表示,小乐坐在小明的正后方,小乐的位置可能是( )
A.(3,5) B.(2,4) C.(1,5) D.(2,6)
20.把一个圆柱形木料削去24立方厘米,得到一个最大的圆锥,圆锥的体积是( )
A.12立方厘米 B.24立方厘米 C.36立方厘米 D.48立方厘米
21.把一个梯形的上底向一个方向延长2分米就变成了一个底是5分米、高是4分米的平行四边形。原来梯形的面积是( )平方分米。
A.20 B.10 C.16 D.32
22.用几个1立方厘米的正方体木块摆了一个物体,如图所示是从不同方向看到的图形,这个物体的体积是( )立方厘米。
A.5 B.6 C.7 D.8
23.1张餐桌可以坐6人,2张餐桌拼在一起可坐10人,如此拼下去,n张餐桌拼在一起可以坐( )人。
A.4n B.4+2n C.2+3n D.2+4n
四.判断题
24.小红在小明的北偏东30°方向,那么小明在小红的南偏西30°方向。
25.将一个圆柱的底面半径先按3:1放大,再按1:2缩小,高不变,这个圆柱的体积是原来的。________
26.同一个圆柱两个底面之间的距离是相等的。
27.将正方形以任意一条边为轴进行旋转得到的立体图形一定是圆柱体。
28.钢材价格第一次提价10%,第二次又提价10%,现价比原价提高了20%。
29.从学校到影院,甲用8分钟,乙用9分钟,甲和乙的速度之比是8:9. .
五.操作题
30.(1)把三角形按1:3作出变化后的图形。
(2)把梯形绕下底左边的顶点顺时针旋转90°,画出旋转后的图形并作出原来梯形的对称轴。
六.应用题
31.用方砖给一间教室铺地。如果用边长为4分米的方砖,需要500块;如果改用边长为8分米的方砖来铺,需要多少块?(用比例解)
32.亮亮看一本故事书,第一天看了全书的,第二天看了全书的,还剩160页没看。
(1)两天一共看了这本书的几分之几?
(2)这本书一共有多少页?
33.修一条800米的路,第一天修了全长的,第二天修了全长的。第二天修了多少米?还剩下多少米没修?
34.在一幅比例尺是1:5000000的地图上,量得甲、乙两地的图上距离是24厘米,一架飞机以800千米/时的速度从甲地飞往乙地,需要多少小时?
35.小强对他们班同学家里有电脑情况作了一个调查,发现他们家里有电脑的有18人,没有电脑的有20人,你能算出小强班上同学家的电脑普及率是多少吗?
36.周大伯把一块长为30米、宽为20米的长方形菜地分成两部分,分别种植黄瓜和番茄。种黄瓜的面积比种番茄的面积少180平方米,黄瓜和番茄各种了多少平方米?小明在思考这一题时,画出了两种不同图形:
(1)根据题意,将两幅图补充完整。
(2)列式解答:
参考答案及试题解析
一.计算题
1.【答案】;21a2;0.43;;;0.05;500;81。
【思路分析】根据分数、小数、百分数加减乘除法的计算方法以及四则混合运算的顺序,直接进行口算即可。
【解答】解:
3a×7a=21a2 0.8﹣0.37=0.43
0.32﹣0.22=0.05 100÷20%=500 0.7×9÷0.7×9=81
【名师点评】本题考查了简单的计算,计算时要细心,注意平时积累经验,提高计算的水平。
2.【答案】35.38,9.01,0.19。
【思路分析】计算小数减法:先把各数的小数点对齐(也就是把相同数位上的数对齐);再按照整数减法的法则进行计算,得数里的小数点要和横线上的小数点对齐(得数的小数部分末尾有0,一般要把0去掉)。
小数乘法法则:先把被乘数和乘数都看作整数,按照整数的乘法法则进行计算,求出整数乘法的积,然后,再看被乘数和乘数一共有几位小数,就从积的右边起数出几位,点上小数点。如果小数的末尾出现0时,根据小数的基本性质,要把它去掉。
小数除法法则:先移动除数的小数点,使它变成整数。除数的小数点向右移动几位,被除数的小数点也向右移动相同的位数(位数不够的补“0”),然后按照除数是整数的除法进行计算。
减法用差+减数=被减数进行验算。
【解答】解:50﹣14.62=35.38
8.5×1.06=9.01
0.798÷4.2=0.19
【名师点评】本题主要考查了小数减法、小数乘法、小数除法的竖式计算方法以及减法的验算方法,注意计算的准确性。
3.【答案】4,4,1110,。
【思路分析】(1)根据加法交换律和加法结合律,以及减法的性质计算;
(2)先算小括号里面的乘法,再算小括号里面的加法,最后算括号外的除法;
(3)先根据积不变规律变形,再根据乘法分配律简算;
(4)先算小括号里面的减法,再算中括号里面的除法,最后算括号外的乘法。
【解答】解:(1)7.5﹣1.26﹣4.74+2.5
=(7.5+2.5)﹣(1.26+4.74)
=10﹣6
=4
(2)6.8÷(0.5+0.3×4)
=6.8÷(0.5+1.2)
=6.8÷1.7
=4
(3)3.6×111+888×0.8
=3.6×111+111×6.4
=111×(3.6+6.4)
=111×10
=1110
(4)
[]
【名师点评】本题考查了四则混合运算,注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算。
二.填空题
4.【答案】225。
【思路分析】通过观察图形可知,两个涂色正方形的周长和等于大正方形的周长,用周长除以4求出大正方形的边长,然后根据正方形的面积=边长×边长,把数据代入公式解答。
【解答】解:60÷4=15(厘米)
15×15=225(平方厘米)
答:大正方形的面积是225平方厘米。
故答案为:225。
【名师点评】此题主要考查正方形的周长公式、面积公式的灵活运用,关键是熟记公式。
5.【答案】1:500000。
【思路分析】根据比例尺的意义作答,即比例尺是图上距离与实际距离的比。
【解答】解:11厘米:55千米
=11厘米:5500000厘米
=1:500000
答:这幅地图的比例尺是1:500000。
故答案为:1:500000。
【名师点评】本题主要考查了比例尺的意义,注意图上距离与实际距离的单位要统一。
6.【答案】113.04。
【思路分析】依据题意可知,利用圆柱的表面积=π×底面半径×底面半径×2+π×底面半径×2×高,然后计算求的表面积。
【解答】解:3.14×3×3×2+3.14×3×2×6
=56.52+113.04
=169.56(平方分米)
169.56113.04(平方分米)
答:球的表面积是113.04平方分米。
故答案为:113.04。
【名师点评】本题考查的是圆柱表面积公式的应用。
7.【答案】见试题解答内容
【思路分析】如图所示,有3种拼法,分别求出的长方形的长和宽,进而利用长方形的周长周长=(长+宽)×2即可求解。
【解答】解:(1)(2×5+3)×2
=13×2
=26(厘米)
(2)(3×5+2)×2
=17×2
=34(厘米)
(3)(3×2+3+2)×2
=11×2
=22(厘米)
22<26<34
答:这个长方形的周长最小是22厘米。
故答案为:22。
【名师点评】此题主要考查长方形的周长的计算方法,关键是求出长方形的长和宽的值。
8.【答案】,35%。
【思路分析】把小数和百分数化成分数,观察题中分数可知,分子分别是1、2、3、4、5,后面一个数比前一个数大1,分母分别是2、5、8、11、14,后一个数比前一个数大3,由此解答本题。
【解答】解:由分析可知:5+1=6,14+3=17,这个分数是;
6+1=7,17+3=20,这个分数是0.35=35%。
故答案为:,35%。
【名师点评】解决本题的关键是找出题中的规律,利用规律去解答。
9.【答案】32。
【思路分析】根据圆内最大正方形的特征可知,这个正方形的对角线的长度等于圆的直径,把这个正方形看作两个完全一样的三角形,根据三角形的面积公式:S=ah÷2,把数据代入公式解答。
【解答】解:8×(8÷2)÷2×2
=8×4÷2×2
=32÷2×2
=32(平方厘米)
答:这个正方形的面积是32平方厘米。
故答案为:32。
【名师点评】此题考查的目的是理解掌握圆内最大正方形的特征及应用,三角形的面积公式、正方形的面积公式及应用。
10.【答案】0.0105,2.75。
【思路分析】低级单位立方厘米化高级单位升除以进率1000。
把45分除以进率60化成0.75小时再加2小时。
【解答】解:10.5cm3=0.0105L
2小时45分=2.75小时
故答案为:0.0105,2.75。
【名师点评】此题考查了体积(容积)的单位换算、时间的单位换算。单位换算首先要弄清是由高级单位化低级单位还是由低级单位化高级单位,其次记住单位间的进率。
11.【答案】38.6。
【思路分析】根据逆运算的方法可知摄氏度=(华氏度﹣32)÷1.8,代入数值进行计算即可。
【解答】解:(101.48﹣32)÷1.8
=69.48÷1.8
=38.6(摄氏度)
也就是38.6摄氏度。
故答案为:38.6。
【名师点评】本题考查小数四则混合运算的计算及应用。理解题意,找出数量关系,列式计算即可。
12.【答案】见试题解答内容
【思路分析】把甲地到乙地的路程看作单位“1”,根据“路程÷时间=速度”分别求出小明的速度和小刚的速度,进而根据题意求比即可.
【解答】解:(1÷12):(1÷15),
:,
=5:4;
故答案为:5:4.
【名师点评】解答此题用到的知识点:(1)比的意义;(2)路程、时间和速度三者之间的关系.
13.【答案】4320。
【思路分析】通过观察图形可知,这个盒子的长等于圆柱底面直径的6倍,盒子的宽等于圆柱底面直径的2倍,盒子的高等于圆柱的高,根据长方体的容积(体积)公式:V=abh,把数据代入公式解答。
【解答】解:(6×6)×(6×2)×10
=36×12×10
=432×10
=4320(立方厘米)
答:这个纸盒的容积是4320立方厘米。
故答案为:4320。
【名师点评】此题主要考查长方体的容积(体积)公式的灵活运用,关键是熟记公式。
14.【答案】(15K+1),(12K+4)。
【思路分析】用1个边长是4厘米正方形面积乘正方形的张数K再减去(K﹣1)×(1×1)平方厘米就得图形面积;用边长是4厘米的正方形周长乘K减去(K﹣1)×(1×4)厘米,就得图像的周长。
【解答】解:4×4×K﹣(K﹣1)×(1×1)
=16K﹣K+1
=(15K+1)平方厘米
4×4×K﹣(K﹣1)×(1×4)
=16K﹣4K+4
=(12K+4)厘米
故答案为:(15K+1),(12K+4)。
【名师点评】仔细观察,找到规律是解决本题的关键。
15.【答案】420。
【思路分析】长方体前面的面积是210平方厘米,即πrh=210平方厘米,圆柱体积=πr2h,据此求出圆柱的体积。
【解答】解:210×(4÷2)
=210×2
=420(立方厘米)
答:圆柱的体积是420立方厘米。
故答案为:420。
【名师点评】理解题目中长方体是如何由圆柱切开拼成的是解答的关键。
16.【答案】14。
【思路分析】由题意可知,每做错或不做一题要丢(5+1)分。假设小华全做对,可得20×5即100分,实际得了64分,丢了(100﹣64)分;用丢的(100﹣64)分除以(5+1)就是做错或没做的题数,最后用20减去做错或没做的题数就是做对的题数。
【解答】解:假设小华全做对。
(20×5﹣64)÷(5+1)
=36÷6
=6
20﹣6=14(道)
答:小华做对了14道。
故答案为:14。
【名师点评】本题属于鸡兔同笼问题,可以用假设法解答,也可以列方程解答。
三.选择题
17.【答案】A
【思路分析】先用“50﹣1﹣2”求出出勤人数,理解出勤率,即出勤的学生人数占全班总人数的百分之几,计算公式:出勤率100%;代入数值,解答即可。
【解答】解:100%=94%
答:六(1)班学生这天的出勤率是94%。
故选:A。
【名师点评】此题属于百分率问题,最大为100%,计算方法为一部分量(或全部量)除以全部量乘百分之百。
18.【答案】D
【思路分析】根据事件发生的可能性大小,哪种情况发生的数量最多,事件发生的可能性就最大;哪种情况发生的数量最少,事件发生的可能性就最小;哪种情况发生的数量一样多,事件发生的可能性就相等,据此分析即可解答。
【解答】解:根据题意可知:第一次旋转,指针箭头停在奇数的位置,得到奖品,剩余3个数都是偶数,所以她得奖的可能性小。
故选:D。
【名师点评】此题考查可能性的大小。掌握判断方法是解答的关键。
19.【答案】D
【思路分析】用数对表示位置时,先表示第几列,再表示第几行,小明坐在教室的位置用数对(2,5)表示,小乐坐在小明的正后方,列不变,行数增加,解答即可。
【解答】解:小明坐在教室的位置用数对(2,5)表示,小乐坐在小明的正后方,小乐的位置可能是(2,6)。
故选:D。
【名师点评】本题考查数对表示位置知识,结合题意分析解答即可。
20.【答案】A
【思路分析】把圆柱形状的木头削成最大的圆锥和原来的圆柱是等底等高的,根据等底等高圆柱体积是圆锥的体积的3倍,可知削去的部分为圆锥的2倍,据此即可解答。
【解答】解:24÷2=12(立方厘米)
答:圆锥的体积是12立方厘米。
故选:A。
【名师点评】此题考查了等底等高的圆锥和圆柱的体积关系。
21.【答案】C
【思路分析】这个梯形的上底是5﹣2=3(分米),下底是5分米,高是4分米,然后根据梯形的面积公式计算即可。
【解答】解:5﹣2=3(分米)
(3+5)×4÷2
=8×4÷2
=32÷2
=16(平方分米)
答:原来梯形的面积是16平方分米。
故选:C。
【名师点评】解答此题的关键是求出原来的梯形的上底的长度。
22.【答案】A
【思路分析】根据从前面和上面观察到的形状可知,该几何体由5个小正方体拼成,据此计算物体的体积即可。
【解答】解:4+1=5(个)
5×1=5(立方厘米)
答:这个物体的体积是5立方厘米。
故选:A。
【名师点评】本题是考查从不同方向观察物体和几何体,关键是培养学生的观察能力。
23.【答案】D
【思路分析】依据题意结合图示可知,1张餐桌可以坐6人,2张餐桌拼在一起可坐(6+4)人,3张餐桌拼在一起可坐(6+4+4)人,4张餐桌拼在一起可坐(6+4+4+4)人,n张餐桌拼在一起可坐[6+4×(n﹣1)]人,由此解答本题。
【解答】解:由分析可知:6+4×(n﹣1)=2+4n(人)
故选:D。
【名师点评】解决本题的关键是找出题中的规律,利用规律去解答。
四.判断题
24.【答案】√
【思路分析】根据位置的相对性可知,描述两个物体之间的相对位置时,方向相反,角度相等,或者先以小明为中心点,找到小红的位置后,再以小红为中心点找小明的位置,从而确定方向,据此解答。
【解答】解:通过分析可知,小红家在小明的北偏东30°方向,那么小明在小红的南偏西30°方向。画图如下:
原题说法正确。
故答案为:√。
【名师点评】本题考查了方向的认识,结合方向的相对性解答即可。
25.【答案】见试题解答内容
【思路分析】把原来圆的半径看作“1”,按3:1放大后的半径是(1×3),再按1:2缩小后的半径是(1×3)。根据圆柱的体积=底面积×高,分别求出原来圆柱的体积和现在的体积,再用现在的体积除以原来圆柱的体积,看结果是不是,如果是原题就正确,否则就错误。
【解答】解:设原来圆的半径看作“1”,按3:1放大后的半径是(1×3),再按1:2缩小后的半径是(1×3),高是h。
π×(1×3)×(1×3)h÷(π×1×1×h)
1
答:这个圆柱的体积是原来的。所以原题说法错误。
故答案为:×。
【名师点评】此题考查的知识点:图形放大与缩小的意义、圆柱体积的计算、分数除法的意义。
26.【答案】√
【思路分析】圆柱的两个底面之间的距离叫做高,圆柱的高相等。
【解答】解:同一个圆柱两个底面之间的距离是相等的。
故原题说法正确。
故答案为:√。
【名师点评】此题考查了圆柱的特征,要熟练掌握。
27.【答案】√
【思路分析】根据圆柱的侧面展开图的特征可知:正方形以任意一条边为轴,旋转一周得到的图形是圆柱,据此即可判断。
【解答】解:根据圆柱体的特征,将正方形以任意一条边为轴进行旋转得到的立体图形一定是圆柱体。这种说法是正确的。
故答案为:√。
【名师点评】根据圆柱的展开图,得出正方形旋转一周得到的是一个圆柱体。
28.【答案】×
【思路分析】先把原件看成单位“1”,第一次提价后的价格是原价的(1+10%),再把第一次提价后的价格看成单位“1”,根据分数乘法的意义,第二次提价后的价格是原价的(1+10%)×(1+10%),进而求出比原价高了百分之几,再与20%比较即可判断。
【解答】解:(1+10%)×(1+10%)
=110%×110%
=121%,
121%﹣1=21%,比原价提高了21%,不是20%。
答:原题干错误。
故答案为:×。
【名师点评】本题的关键是把单位“1”统一到原价上,求出现价比原价高百分之几,再比较。
29.【答案】见试题解答内容
【思路分析】根据题意,把从学校走到公园的路程看作单位“1”,可知甲、乙的速度分别是、,然后化简比即可.
【解答】解::9:8
答:甲和乙的速度比为9:8.
故答案为:×.
【名师点评】此题关键先求出两人的速度,再化简比.
五.操作题
30.【答案】(1)、(2)
【思路分析】(1)三角形看作底为6格,高为3格的三角形,根据图形缩小的意义,把这个三角形对应的底、高均缩小到原来的,对应角大小不变,所得到的图形就是原图形按1:3缩小后的图形。
(2)根据旋转的特征,梯形绕下底左边的顶点顺时针旋转90°,此顶点的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。旋转后的图形仍为等腰梯形,是轴对称图形,只有1条对称轴,即过上、下底中点的直线。
【解答】解:(1)、(2)画图如下:
【名师点评】此题考查了图形的放大与缩小、作旋转一定度数后的图形、确定轴对称图形对称轴的条数及位置。
六.应用题
31.【答案】125块。
【思路分析】根据题意可知:每块方砖的面积和所需的块数成反比例。据此设需要x块砖,然后列出方程即可求解。
【解答】解:设需要x块。
8×8×x=4×4×500
64x=8000
x=125
答:需要125块。
【名师点评】解答此题的关键是判断出方砖的块数与方砖的面积成反比例,注意题中的4分米与5分米是方砖的边长不是方砖的面积。
32.【答案】(1);
(2)700页。
【思路分析】(1)把这本故事书的页看作单位“1”,根据加法的意义,用加法解答。
(2)把这本故事书的页看作单位“1”,剩下没有看的页占这本故事书的(1),根据已知一个数的几分之几是多少,求这个数,用除法解答。
【解答】解:(1)
答:两天一共看了这本书的。
(2)160÷(1)
=160÷(1)
=160
=160
=700(页)
答:这本书一共有700页。
【名师点评】此题考查的目的是理解分数加法、分数除法的意义,掌握分数加法、分数除法的计算法则及应用。
33.【答案】320米;240米。
【思路分析】第二天修的长度=全长,剩下的长度=总长×(1﹣第一天修了全长的几分之几﹣第二天修了全长的几分之几),由此列式计算即可。
【解答】解:(米)
(米)
答:第二天修了320米,还剩240米没修。
【名师点评】解决本题的关键是找出题中数量关系。
34.【答案】1.5小时。
【思路分析】根据实际距离=图上距离÷比例尺,先求出甲、乙两地实际距离,再根据时间=路程÷速度,列式解答即可。
【解答】解:(厘米)
120000000厘米=1200千米
1200÷800=1.5(小时)
答:需要1.5小时。
【名师点评】熟练掌握比例尺公式,是解答此题的关键。
35.【答案】47.4%。
【思路分析】电脑的普及率=家里有电脑同学人数÷班级总人数×100%,班级总人数=家里有电脑同学人数+没有电脑的同学人数,据此列式计算即可。
【解答】解:18÷(18+20)×100%
=18÷38×100%
≈47.4%
答:小强班上同学家的电脑普及率约是47.4%。
【名师点评】本题主要考查百分率在生活中的应用。
36.【答案】黄瓜种了210平方米,番茄种了390平方米。
【思路分析】(1)根据小明未完成的图示继续补全图片;
(2)根据“长方形面积=长×宽”计算出长方形菜地的面积,即种植黄瓜和番茄的面积之和,根据和差公式“较大数=(和+差)÷2”求出番茄种植面积,用种植黄瓜和番茄的面积之和减去番茄种植面积即是黄瓜种植面积。
【解答】解:(1)如下图所示:
(2)30×20=600(平方米)
(600+180)÷2=390(平方米)
600﹣390=210(平方米)
答:黄瓜种了210平方米,番茄种了390平方米。
【名师点评】本题考查了和差公式的应用以及长方形面积的计算。
21世纪教育网(www.21cnjy.com)
同课章节目录
