《巩固卷》——5.6.4组合图形的面积(分层作业)(含解析)-2025-2026学年五年级上册数学(人教版)
文档属性
| 名称 | 《巩固卷》——5.6.4组合图形的面积(分层作业)(含解析)-2025-2026学年五年级上册数学(人教版) |
|
|
| 格式 | docx | ||
| 文件大小 | 506.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-16 10:50:32 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
《巩固卷》——5.6.4组合图形的面积(分层作业)-2025-2026学年五年级上册数学(人教版)
一、单选题
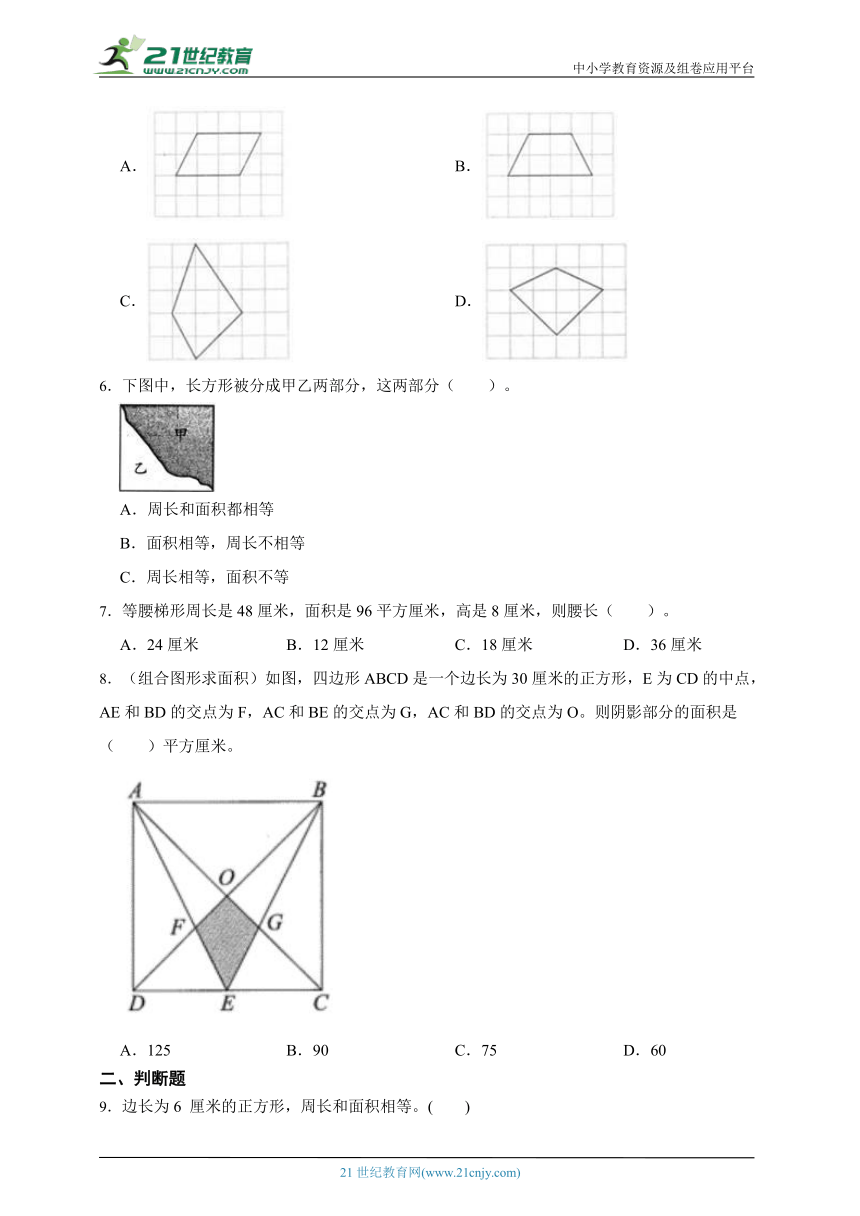
1.在下面的方格纸上,有四个图形,( )的面积与①一样大。
A.③④ B.②③ C.②③④
2.(组合图形求面积)如图,在长方形ABCE中,AE=10厘米,AB=8厘米。三角形ACD的面积是20平方厘米,那么梯形ABDE的面积是( )平方厘米。
A.100 B.160 C.200 D.300
3.如图所示,长方形被分为甲、乙两部分,这两部分( )。
A.周长相等,面积不相等 B.周长和面积都不相等
C.周长和面积都相等 D.面积相等,周长不相等
4.下面的四个大正方形面积相等,阴影部分的面积最小的是( )。
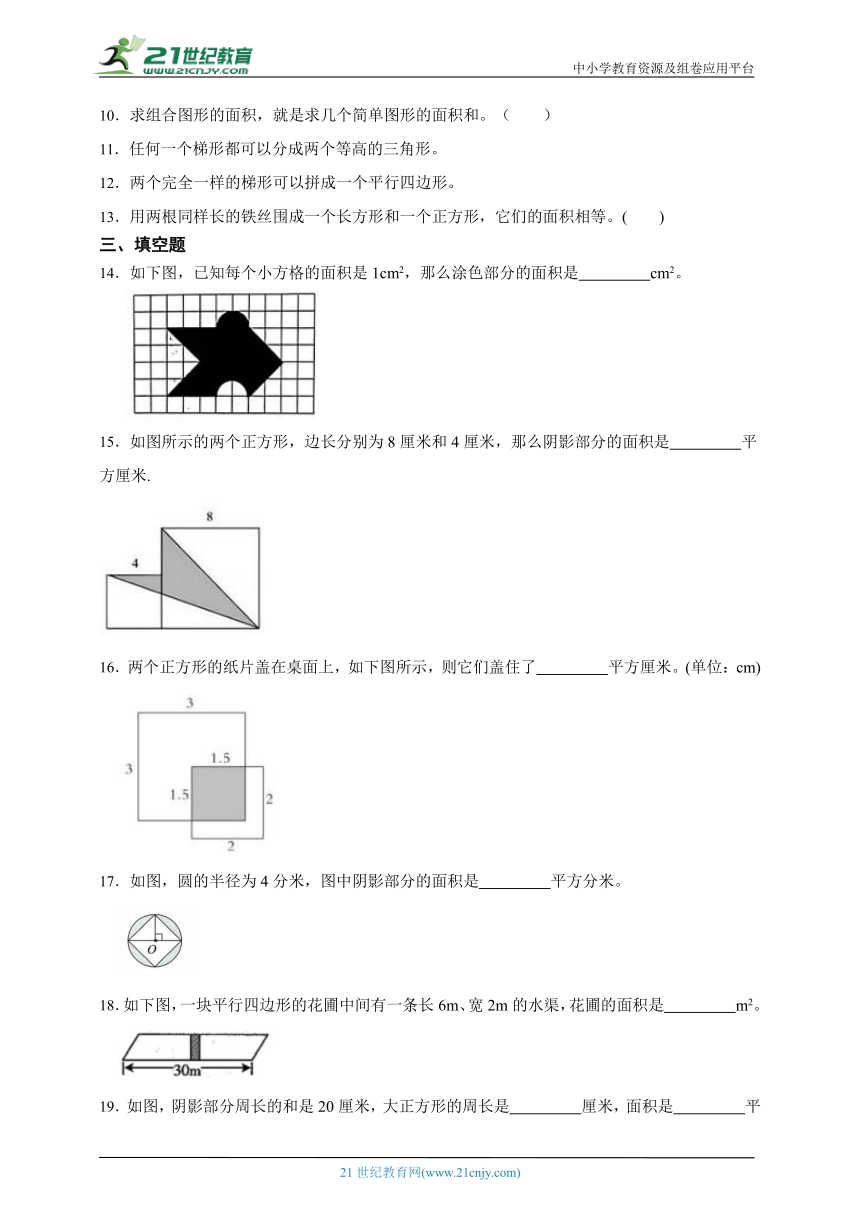
A. B.
C. D.
5.下面每个小正方形的面积是1平方厘米,面积不是6平方厘米的四边形是( )。
A. B.
C. D.
6.下图中,长方形被分成甲乙两部分,这两部分( )。
A.周长和面积都相等
B.面积相等,周长不相等
C.周长相等,面积不等
7.等腰梯形周长是48厘米,面积是96平方厘米,高是8厘米,则腰长( )。
A.24厘米 B.12厘米 C.18厘米 D.36厘米
8.(组合图形求面积)如图,四边形ABCD是一个边长为30厘米的正方形,E为CD的中点,AE和BD的交点为F,AC和BE的交点为G,AC和BD的交点为O。则阴影部分的面积是( )平方厘米。
A.125 B.90 C.75 D.60
二、判断题
9.边长为6 厘米的正方形,周长和面积相等。( )
10.求组合图形的面积,就是求几个简单图形的面积和。( )
11.任何一个梯形都可以分成两个等高的三角形。
12.两个完全一样的梯形可以拼成一个平行四边形。
13.用两根同样长的铁丝围成一个长方形和一个正方形,它们的面积相等。( )
三、填空题
14.如下图,已知每个小方格的面积是1cm2,那么涂色部分的面积是 cm2。
15.如图所示的两个正方形,边长分别为8厘米和4厘米,那么阴影部分的面积是 平方厘米.
16.两个正方形的纸片盖在桌面上,如下图所示,则它们盖住了 平方厘米。(单位:cm)
17.如图,圆的半径为4分米,图中阴影部分的面积是 平方分米。
18.如下图,一块平行四边形的花圃中间有一条长6m、宽2m的水渠,花圃的面积是 m2。
19.如图,阴影部分周长的和是20厘米,大正方形的周长是 厘米,面积是 平方厘米。
20.如图,将四边形的四条边、、、分别延长两倍至点、、、,若四边形的面积为5,则四边形的面积是 。
21.如图,一枚半径为1cm的圆形游戏币在边长为4cm的正方形内任意移动,则在正方形内,游戏币不能到达的部分面积为 cm2(π取3.14)
四、操作题
22.下面的方格纸上,每个代表1平方厘米。
(1)图中涂色部分的面积是 平方厘米。
(2)请在图中画一个面积是15平方厘米的长方形。
五、解决问题
23.张叔叔要粉刷自己的工作室,工作室的一面墙的平面图如图所示,如果每平方米要用2.5千克涂料,那么粉刷这面墙至少要用多少千克涂料?
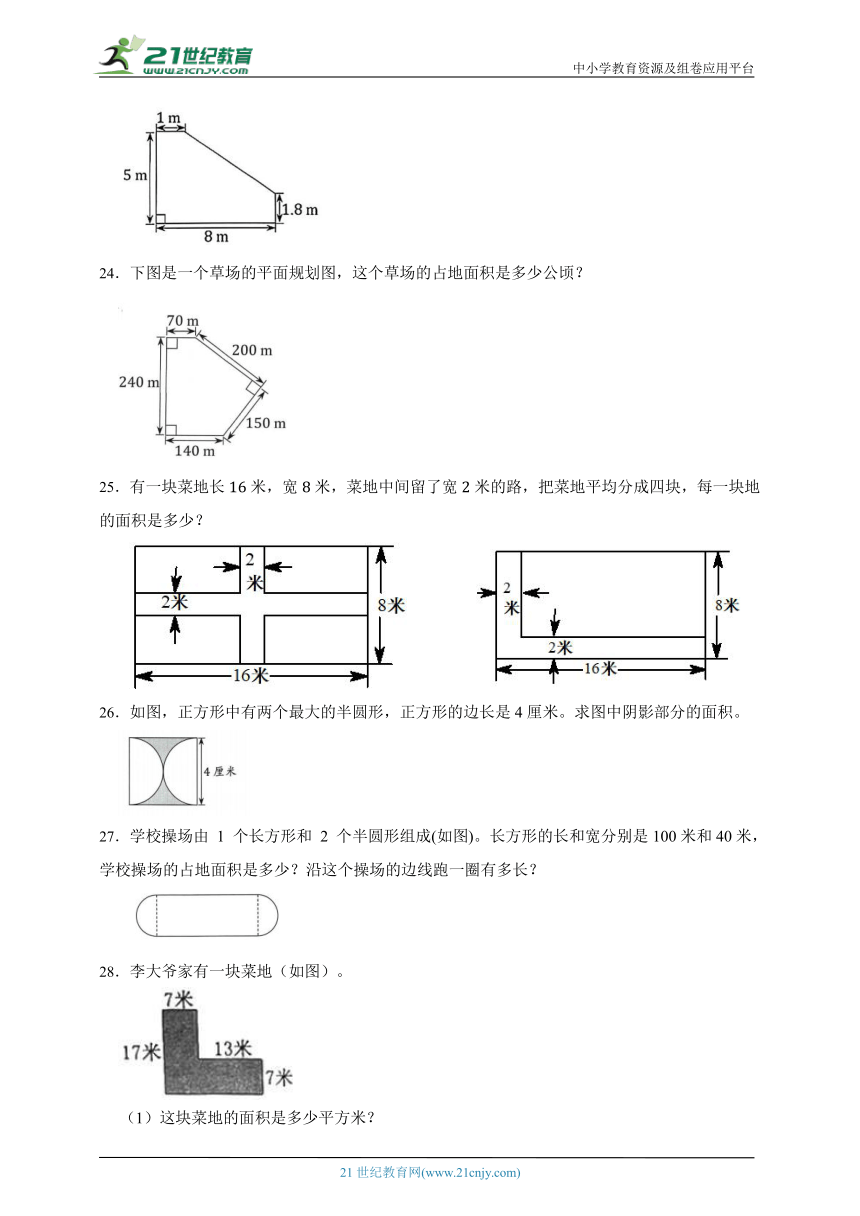
24.下图是一个草场的平面规划图,这个草场的占地面积是多少公顷?
25.有一块菜地长米,宽米,菜地中间留了宽米的路,把菜地平均分成四块,每一块地的面积是多少?
26.如图,正方形中有两个最大的半圆形,正方形的边长是4厘米。求图中阴影部分的面积。
27.学校操场由 1 个长方形和 2 个半圆形组成(如图)。长方形的长和宽分别是100米和40米,学校操场的占地面积是多少?沿这个操场的边线跑一圈有多长?
28.李大爷家有一块菜地(如图)。
(1)这块菜地的面积是多少平方米?
(2)如果用篱笆把这块菜地围起来,要用多长的篱笆?
29.如图,一块梯形土地中有一条长16米、宽1米的长方形小路,其余的部分为草地。求草地的面积。
30.如图是学校一个正方形花圃的设计图,图中阴影部分是花圃,空白部分是草坪.求花圃的面积是多少平方米?
答案解析部分
1.【答案】A
2.【答案】A
【解析】【解答】由题图可知,S△ACD=S△ECD(同底等高的三角形面积相等)
10×8+20=100(平方厘米)
故答案为:A
【分析】由图可知,三角形ACD和三角形ECD是同底等高,所以三角形ACD的面积和三角形ECD的面积相等。由题干已知,三角形ACD的面积的20平方厘米,所以三角形ECD的面积是20平方厘米;长方形面积=底×高,即长方形ABCE的面积=10×8=80平方厘米,梯形的面积=长方形ABCE的面积+三角形ECD的面积,计算出梯形ABDE的面积即可。
3.【答案】A
【解析】【解答】
如图所示,长方形被分为甲、乙两部分,这两部分:周长相等,面积不相等。
故答案为:A.
【分析】观察图可知,甲、乙的周长都等于一条长+一条宽+中间的折线部分,所以周长相等;
对比面积可知,甲与乙的面积不相等,据此解答.
4.【答案】C
【解析】【解答】解:阴影部分的面积最小是C项。
故答案为:C。
【分析】从图中可以看出,A、B两项阴影部分的面积相等,是以正方形的边长为半径的圆的面积,C项中的阴影部分是2个正方形,D项中的阴影部分是3个正方形,所以C项中阴影部分的面积最小。
5.【答案】C
【解析】【解答】选项A,,3×2=6(平方厘米);
选项B,,(2+4)×2÷2=6(平方厘米);
选项C,,3×3÷2+3×2÷2=7.5(平方厘米);
选项D,,4×1÷2+4×2÷2=6(平方厘米)。
故答案为:C。
【分析】根据题意,分别求出各选项图形的面积,再判断,选项A,平行四边形的面积=底×高;选项B,梯形的面积=(上底+下底)×高÷2;选项C、D的面积分别等于两个三角形的面积之和,据此计算再对比。
6.【答案】C
【解析】【解答】解:观察图形可得甲的周长=乙的周长;甲的面积>乙的面积。
故答案为:C。
【分析】观察图形可得甲的周长=长方形的一条长+长方形的一条宽+曲线长,乙的周长=长方形的一条长+长方形的一条宽+曲线长;连接左上方和右下方长方形的两个顶点即可判断出甲的面积和乙面积的大小。
7.【答案】B
【解析】【解答】根据题干可得,梯形的上底与下底的和为:96×2÷8=24(厘米)
梯形的腰长为:
(48-24)÷2
=24÷2
=12〔厘米〕
故选:B
【分析】根据题干,可以利用梯形的面积公式先求出上底加下底的和是多少,再利用周长求得两腰的长度。
8.【答案】C
【解析】【解答】连接OE,四边形ABCD 是一个边长是30厘米的正方形,E是CD的中点。
正方形ABCD ═ ×30×30 = 112.5(平方厘米)
BO=DO,CE=DE,OE是△BCD的中位线。
从而
(平方厘米)
同理可得 : (平方厘米)
(平方厘米)
故答案为:C。
【分析】因为E是正方形边的中点,所以可得△ADE的面积等于正方形面积的四分之一,△AFB∽△EDF,则DE:AB=EF:FA=1:2,可以得到△EDF的面积=×△ADE的面积=×正方形面积=×正方形面积。同理可证,△CEG的面积=×正方形面积。进而求出阴影部分的面积即可。
9.【答案】错误
【解析】【解答】解:6×4=24(厘米)
6×6=36(平方厘米),面积和周长无法比较大小。
故答案为:错误。
【分析】正方形的周长和面积:①意义不同,正方形的面积是指正方形所占平面的大小,而正方形的周长是指围成正方形一周的长度;②计算方法不同,正方形的面积=边长×边长,而正方形的周长=边长×4;③计量单位不同,面积用面积单位,而周长用长度单位,所以面积和周长无法比较大小。
10.【答案】正确
【解析】【解答】解:求组合图形的面积,就是求几个简单图形的面积和,原题干说法正确。
故答案为:正确。
【分析】由几个简单的图形组合在一起就是组合图形,求组合图形的面积,就是求几个简单图形的面积和。
11.【答案】正确
【解析】【解答】根据梯形的定义可知,有一组对边平行的四边形叫平行四边形。因为当梯形分成两个三角形时是以梯形的上底和下底为三角形的一条底边,又因为梯形的上下底是一组平行线,所以它们之间的距离是相等的,所以任何一个梯形都可以分成两个等高的三角形的说法是正确的。
故答案为:正确。
【分析】根据梯形的定义可知,有一组对边平行的四边形叫平行四边形;因为当梯形分成两个三角形时是以梯形的上底和下底为三角形的一条底边,又因为梯形的上下底是一组平行线,所以它们之间的距离是相等的,由此判断即可。
12.【答案】正确
【解析】【解答】因梯形的上底和下底平行,组成后图形的对边(上底+下底)等于(下底+上底),且平行,所以组成后的图形是平行四边形。
故答案为:正确。
【分析】因为平行四边形的对边平行且相等,两个完全一样的梯形可以以腰为公共边,其上底和下底分别对另一梯形的下底和上底,因梯形的上底和下底平行,组成后图形的对边(上底+下底)等于(下底+上底),且平行,据此解答。
13.【答案】错误
【解析】【解答】解:假设这两根铁丝的长度都是16厘米:
长方形:16÷2=8(厘米)
6+2=8(厘米),此时长方形的长为6厘米,宽为2厘米,则面积为:6×2=12(平方厘米)
正方形:16÷4=4(厘米),则正方形的边长为4厘米,因此面积为:4×4=16(平方厘米)
16厘米=16厘米,16平方厘米>12平方厘米
因此用两根同样长的铁丝围成一个长方形和一个正方形,它们的周长相等,面积不相等。
故答案为:错误。
【分析】封闭图形一周的长度是这个图形的周长;面积是指物体所占的平面图形的大小,周长相等的长方形和正方形, 正方形的面积较大。
14.【答案】20
【解析】【解答】解:如图:
5×4=20(平方厘米)
故答案为:20。
【分析】通过平移可以看出,涂色部分的面积是一个长方形,长方形的面积=长×宽。
15.【答案】24
【解析】【解答】
三角形 CDB 面积:(8+4)x4÷2=12x4÷2=48÷2=24(cm2)
三角形 ABE 面积:8x8÷2=64÷2=32(cm2)
阴影部分面积:8x8+4x4-24-32=24 (cm2)
故答案为:24
【分析】阴影部分面积可以用两个正方形面积减去三角形 CDB 和三角形 ABE 的面积求得。
16.【答案】10.75
【解析】【解答】解:2×2+3×3-1.5×1.5
=13-2.25
=10.75(cm2)。
故答案为:10.75。
【分析】它们盖住的面积=小正方形的边长×边长+大正方形的边长×边长-重叠部分的边长×边长。
17.【答案】18.24
【解析】【解答】解:3.14×42-4×2×4×2÷2
=50.24-32
=18.24(平方分米)
故答案为:18.24。
【分析】已知圆的半径是4分米,根据圆的面积公式:S=πr2,得到圆的面积是3.14×42;正方形的对角线长度是4×2=8(分米),根据正方形的面积=对角线×对角线÷2,计算得到正方形的面积是4×2×4×2÷2,然后用晕的面积减去正方形的面积,即可得到阴影部分的面积。
18.【答案】168
【解析】【解答】解:30×6-6×2
=180-12
=168(平方米)
故答案为:168。
【分析】花圃的面积=平行四边形的底×高-长方形水渠的长×宽。
19.【答案】20;25
【解析】【解答】阴影部分周长=大正方形的周长=20厘米;(20÷4)2=52=5×5=25(平方厘米)。
故答案为:20;25。
【分析】如图所示,通过平移可得:大正方形的周长=阴影部分周长的总和;即可求得大正方形的周长。利用“正方形的面积=边长2”即可求得大正方形的面积。
20.【答案】60
【解析】【解答】解:连接 、 。
由于 , ,
于是 ,
同理 。
于是 。
再由于 , ,
于是 ,
同理 。
于是 。
那么 故答案为:60
【分析】连接 、,根据BE,BF和AB,BC的关系得到三角形BEF和三角形ABC的面积关系,同理可以得出三角形HDG和三角形ADC的面积关系,根据这些关系可以得出它们和四边形ABCD的面积关系,用相同的方法可以得出四边形ABCD和三角形AEH,CFG,ABD,CBD的关系,综合他们的关系以及已知条件,即可解出四边形EFGH的面积
21.【答案】0.86
【解析】【解答】解:1+1=2(cm),
2×2-3.14×1
=4-3.14
=0.86(cm )
故答案为:0.86。
【分析】不能达到的部分实际就是四个角的部分,这四部分的面积实际就是边长2厘米的正方形面积减去一个半径1厘米的圆面积。
22.【答案】(1)10
(2)解:长方形的长画5厘米,宽画3厘米,面积就是15平方厘米,
【解析】【解答】解:(1)涂色部分有10格,图中涂色部分的面积是10平方厘米。
故答案为:(1)10。
【分析】(1)涂色部分下面的三角形,通过观察有2个小正方形,据此解答;
(2)长方形的面积=长×宽,据此作图。
23.【答案】解:8×5=40(平方米)
(8-1)×(5-1.8)÷2 =11.2(平方米)
(40-11.2)×2.5 = 72(千克)
答: 粉刷这面墙至少要用72千克涂料。
【解析】【分析】如图:,墙的面积=长方形的面积-三角形的面积,长方形的面积=长×宽,三角形的面积=底×高÷2,然后用墙的面积乘每平方米用涂料的重量,据此解答。
24.【答案】解:(70+140)×240÷2 =25200(m2)
150×200÷2=15000(m2)
25200+15000=40200(m2)
40200m2=4.02公顷
答:这个草场的占地面积是4.02公顷。
【解析】【分析】如图,,草场的占地面积=梯形面积+三角形面积,梯形的面积=(上底+下底)×高÷2,三角形的面积=底×高÷2,据此解答。
25.【答案】解:根据题意,可得
(16-2)×(8-2)÷4
=14×6÷4
=84÷4
=21(平方米)
答:每一块地的面积是21平方米.
【解析】【分析】通过平移把四块菜地转化为:长是(16-2)米,宽是(8-2)米,根据长方形的面积公式:s=ab,把数据代入公式求出总面积,然后除以4即可.
26.【答案】解:半径: 4÷2 =2(厘米)
(平方厘米)
答:图中阴影部分的面积是3.44平方厘米。
【解析】【分析】观察图形,半圆的直径是4厘米,根据直径=半径×2,可以得到半圆的半径就是4÷2 =2(厘米),然后根据圆的面积公式:S=πr2,代入数据求出圆的面积,又已知正方形的边长是4厘米,根据正方形的面积公式:S=边长×边长,计算得出正方形的面积,最后用正方形的面积减去圆的面积,即可得到阴影部分的面积。
27.【答案】解:半径: 40÷2 =20(米)
面积:
一圈长: 100×2+3.14×40=325.6(m)
答:学校操场的面积是5256平方米,沿这个操场的边线跑一圈有325.6米长。
【解析】【分析】观察图形,学校操场的占地面积就是直径为40米的圆的面积加上长100米,宽40米长方形的面积;根据圆的半径=直径2,计算得到圆的半径是40÷2 =20(米),然后根据长方形的面积公式:S=长×宽,圆的面积公式:S=πr2,代入数据计算即可得到这个操场的占地面积;沿这个操场的边线跑一圈的长度就是直径为40米的圆的周长加上两条100米的长度,根据圆的周长公式:C=πd,代入数据计算即可。
28.【答案】(1)解:17×7+13×7
=119+91
=210(平方米)
答:这块菜地的面积是210平方米。
(2)解:7+13=20(米)
(20+17)×2
=37×2
=74(米)
答:要用74米长的篱笆。
【解析】【分析】(1)这块菜地的面积=左边长方形的面积+右边长方形的面积;其中,长方形的面积=长×宽;
(2)利用平移的方法,把这个图形的边经过平移变成长方形,要用篱笆的长度=长方形的周长=(长+宽)×2。
29.【答案】解:(12+25)×16÷2-16×1
=296-16
=280(m2)
答:草地的面积是280平方米。
【解析】【分析】草地的面积=(整个梯形的上底+下底)×高÷2-中间小路的长×宽。
30.【答案】解:如图所示,作出辅助线,
阴影部分的面积=10×10﹣(10×10﹣3×2)÷2,
=100﹣(100﹣6)÷2,
=100﹣94÷2,
=100﹣47,
=53(平方米);
答:花圃的面积是53平方米.
【解析】【分析】由题意可知:四个角就是四个直角三角形;我们可以把它画成4个长方形,最后就有一个黑色长方形,把整个正方形的面积减去黑色部分长方形的面积再除于2就是四个直角三角形的面积总和,进而用正方形的面积减去四个直角三角形的面积总和,就是花圃的面积.解答此题的关键是将阴影部分进行分割,进而转化成容易面积的图形,问题得解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
《巩固卷》——5.6.4组合图形的面积(分层作业)-2025-2026学年五年级上册数学(人教版)
一、单选题
1.在下面的方格纸上,有四个图形,( )的面积与①一样大。
A.③④ B.②③ C.②③④
2.(组合图形求面积)如图,在长方形ABCE中,AE=10厘米,AB=8厘米。三角形ACD的面积是20平方厘米,那么梯形ABDE的面积是( )平方厘米。
A.100 B.160 C.200 D.300
3.如图所示,长方形被分为甲、乙两部分,这两部分( )。
A.周长相等,面积不相等 B.周长和面积都不相等
C.周长和面积都相等 D.面积相等,周长不相等
4.下面的四个大正方形面积相等,阴影部分的面积最小的是( )。
A. B.
C. D.
5.下面每个小正方形的面积是1平方厘米,面积不是6平方厘米的四边形是( )。
A. B.
C. D.
6.下图中,长方形被分成甲乙两部分,这两部分( )。
A.周长和面积都相等
B.面积相等,周长不相等
C.周长相等,面积不等
7.等腰梯形周长是48厘米,面积是96平方厘米,高是8厘米,则腰长( )。
A.24厘米 B.12厘米 C.18厘米 D.36厘米
8.(组合图形求面积)如图,四边形ABCD是一个边长为30厘米的正方形,E为CD的中点,AE和BD的交点为F,AC和BE的交点为G,AC和BD的交点为O。则阴影部分的面积是( )平方厘米。
A.125 B.90 C.75 D.60
二、判断题
9.边长为6 厘米的正方形,周长和面积相等。( )
10.求组合图形的面积,就是求几个简单图形的面积和。( )
11.任何一个梯形都可以分成两个等高的三角形。
12.两个完全一样的梯形可以拼成一个平行四边形。
13.用两根同样长的铁丝围成一个长方形和一个正方形,它们的面积相等。( )
三、填空题
14.如下图,已知每个小方格的面积是1cm2,那么涂色部分的面积是 cm2。
15.如图所示的两个正方形,边长分别为8厘米和4厘米,那么阴影部分的面积是 平方厘米.
16.两个正方形的纸片盖在桌面上,如下图所示,则它们盖住了 平方厘米。(单位:cm)
17.如图,圆的半径为4分米,图中阴影部分的面积是 平方分米。
18.如下图,一块平行四边形的花圃中间有一条长6m、宽2m的水渠,花圃的面积是 m2。
19.如图,阴影部分周长的和是20厘米,大正方形的周长是 厘米,面积是 平方厘米。
20.如图,将四边形的四条边、、、分别延长两倍至点、、、,若四边形的面积为5,则四边形的面积是 。
21.如图,一枚半径为1cm的圆形游戏币在边长为4cm的正方形内任意移动,则在正方形内,游戏币不能到达的部分面积为 cm2(π取3.14)
四、操作题
22.下面的方格纸上,每个代表1平方厘米。
(1)图中涂色部分的面积是 平方厘米。
(2)请在图中画一个面积是15平方厘米的长方形。
五、解决问题
23.张叔叔要粉刷自己的工作室,工作室的一面墙的平面图如图所示,如果每平方米要用2.5千克涂料,那么粉刷这面墙至少要用多少千克涂料?
24.下图是一个草场的平面规划图,这个草场的占地面积是多少公顷?
25.有一块菜地长米,宽米,菜地中间留了宽米的路,把菜地平均分成四块,每一块地的面积是多少?
26.如图,正方形中有两个最大的半圆形,正方形的边长是4厘米。求图中阴影部分的面积。
27.学校操场由 1 个长方形和 2 个半圆形组成(如图)。长方形的长和宽分别是100米和40米,学校操场的占地面积是多少?沿这个操场的边线跑一圈有多长?
28.李大爷家有一块菜地(如图)。
(1)这块菜地的面积是多少平方米?
(2)如果用篱笆把这块菜地围起来,要用多长的篱笆?
29.如图,一块梯形土地中有一条长16米、宽1米的长方形小路,其余的部分为草地。求草地的面积。
30.如图是学校一个正方形花圃的设计图,图中阴影部分是花圃,空白部分是草坪.求花圃的面积是多少平方米?
答案解析部分
1.【答案】A
2.【答案】A
【解析】【解答】由题图可知,S△ACD=S△ECD(同底等高的三角形面积相等)
10×8+20=100(平方厘米)
故答案为:A
【分析】由图可知,三角形ACD和三角形ECD是同底等高,所以三角形ACD的面积和三角形ECD的面积相等。由题干已知,三角形ACD的面积的20平方厘米,所以三角形ECD的面积是20平方厘米;长方形面积=底×高,即长方形ABCE的面积=10×8=80平方厘米,梯形的面积=长方形ABCE的面积+三角形ECD的面积,计算出梯形ABDE的面积即可。
3.【答案】A
【解析】【解答】
如图所示,长方形被分为甲、乙两部分,这两部分:周长相等,面积不相等。
故答案为:A.
【分析】观察图可知,甲、乙的周长都等于一条长+一条宽+中间的折线部分,所以周长相等;
对比面积可知,甲与乙的面积不相等,据此解答.
4.【答案】C
【解析】【解答】解:阴影部分的面积最小是C项。
故答案为:C。
【分析】从图中可以看出,A、B两项阴影部分的面积相等,是以正方形的边长为半径的圆的面积,C项中的阴影部分是2个正方形,D项中的阴影部分是3个正方形,所以C项中阴影部分的面积最小。
5.【答案】C
【解析】【解答】选项A,,3×2=6(平方厘米);
选项B,,(2+4)×2÷2=6(平方厘米);
选项C,,3×3÷2+3×2÷2=7.5(平方厘米);
选项D,,4×1÷2+4×2÷2=6(平方厘米)。
故答案为:C。
【分析】根据题意,分别求出各选项图形的面积,再判断,选项A,平行四边形的面积=底×高;选项B,梯形的面积=(上底+下底)×高÷2;选项C、D的面积分别等于两个三角形的面积之和,据此计算再对比。
6.【答案】C
【解析】【解答】解:观察图形可得甲的周长=乙的周长;甲的面积>乙的面积。
故答案为:C。
【分析】观察图形可得甲的周长=长方形的一条长+长方形的一条宽+曲线长,乙的周长=长方形的一条长+长方形的一条宽+曲线长;连接左上方和右下方长方形的两个顶点即可判断出甲的面积和乙面积的大小。
7.【答案】B
【解析】【解答】根据题干可得,梯形的上底与下底的和为:96×2÷8=24(厘米)
梯形的腰长为:
(48-24)÷2
=24÷2
=12〔厘米〕
故选:B
【分析】根据题干,可以利用梯形的面积公式先求出上底加下底的和是多少,再利用周长求得两腰的长度。
8.【答案】C
【解析】【解答】连接OE,四边形ABCD 是一个边长是30厘米的正方形,E是CD的中点。
正方形ABCD ═ ×30×30 = 112.5(平方厘米)
BO=DO,CE=DE,OE是△BCD的中位线。
从而
(平方厘米)
同理可得 : (平方厘米)
(平方厘米)
故答案为:C。
【分析】因为E是正方形边的中点,所以可得△ADE的面积等于正方形面积的四分之一,△AFB∽△EDF,则DE:AB=EF:FA=1:2,可以得到△EDF的面积=×△ADE的面积=×正方形面积=×正方形面积。同理可证,△CEG的面积=×正方形面积。进而求出阴影部分的面积即可。
9.【答案】错误
【解析】【解答】解:6×4=24(厘米)
6×6=36(平方厘米),面积和周长无法比较大小。
故答案为:错误。
【分析】正方形的周长和面积:①意义不同,正方形的面积是指正方形所占平面的大小,而正方形的周长是指围成正方形一周的长度;②计算方法不同,正方形的面积=边长×边长,而正方形的周长=边长×4;③计量单位不同,面积用面积单位,而周长用长度单位,所以面积和周长无法比较大小。
10.【答案】正确
【解析】【解答】解:求组合图形的面积,就是求几个简单图形的面积和,原题干说法正确。
故答案为:正确。
【分析】由几个简单的图形组合在一起就是组合图形,求组合图形的面积,就是求几个简单图形的面积和。
11.【答案】正确
【解析】【解答】根据梯形的定义可知,有一组对边平行的四边形叫平行四边形。因为当梯形分成两个三角形时是以梯形的上底和下底为三角形的一条底边,又因为梯形的上下底是一组平行线,所以它们之间的距离是相等的,所以任何一个梯形都可以分成两个等高的三角形的说法是正确的。
故答案为:正确。
【分析】根据梯形的定义可知,有一组对边平行的四边形叫平行四边形;因为当梯形分成两个三角形时是以梯形的上底和下底为三角形的一条底边,又因为梯形的上下底是一组平行线,所以它们之间的距离是相等的,由此判断即可。
12.【答案】正确
【解析】【解答】因梯形的上底和下底平行,组成后图形的对边(上底+下底)等于(下底+上底),且平行,所以组成后的图形是平行四边形。
故答案为:正确。
【分析】因为平行四边形的对边平行且相等,两个完全一样的梯形可以以腰为公共边,其上底和下底分别对另一梯形的下底和上底,因梯形的上底和下底平行,组成后图形的对边(上底+下底)等于(下底+上底),且平行,据此解答。
13.【答案】错误
【解析】【解答】解:假设这两根铁丝的长度都是16厘米:
长方形:16÷2=8(厘米)
6+2=8(厘米),此时长方形的长为6厘米,宽为2厘米,则面积为:6×2=12(平方厘米)
正方形:16÷4=4(厘米),则正方形的边长为4厘米,因此面积为:4×4=16(平方厘米)
16厘米=16厘米,16平方厘米>12平方厘米
因此用两根同样长的铁丝围成一个长方形和一个正方形,它们的周长相等,面积不相等。
故答案为:错误。
【分析】封闭图形一周的长度是这个图形的周长;面积是指物体所占的平面图形的大小,周长相等的长方形和正方形, 正方形的面积较大。
14.【答案】20
【解析】【解答】解:如图:
5×4=20(平方厘米)
故答案为:20。
【分析】通过平移可以看出,涂色部分的面积是一个长方形,长方形的面积=长×宽。
15.【答案】24
【解析】【解答】
三角形 CDB 面积:(8+4)x4÷2=12x4÷2=48÷2=24(cm2)
三角形 ABE 面积:8x8÷2=64÷2=32(cm2)
阴影部分面积:8x8+4x4-24-32=24 (cm2)
故答案为:24
【分析】阴影部分面积可以用两个正方形面积减去三角形 CDB 和三角形 ABE 的面积求得。
16.【答案】10.75
【解析】【解答】解:2×2+3×3-1.5×1.5
=13-2.25
=10.75(cm2)。
故答案为:10.75。
【分析】它们盖住的面积=小正方形的边长×边长+大正方形的边长×边长-重叠部分的边长×边长。
17.【答案】18.24
【解析】【解答】解:3.14×42-4×2×4×2÷2
=50.24-32
=18.24(平方分米)
故答案为:18.24。
【分析】已知圆的半径是4分米,根据圆的面积公式:S=πr2,得到圆的面积是3.14×42;正方形的对角线长度是4×2=8(分米),根据正方形的面积=对角线×对角线÷2,计算得到正方形的面积是4×2×4×2÷2,然后用晕的面积减去正方形的面积,即可得到阴影部分的面积。
18.【答案】168
【解析】【解答】解:30×6-6×2
=180-12
=168(平方米)
故答案为:168。
【分析】花圃的面积=平行四边形的底×高-长方形水渠的长×宽。
19.【答案】20;25
【解析】【解答】阴影部分周长=大正方形的周长=20厘米;(20÷4)2=52=5×5=25(平方厘米)。
故答案为:20;25。
【分析】如图所示,通过平移可得:大正方形的周长=阴影部分周长的总和;即可求得大正方形的周长。利用“正方形的面积=边长2”即可求得大正方形的面积。
20.【答案】60
【解析】【解答】解:连接 、 。
由于 , ,
于是 ,
同理 。
于是 。
再由于 , ,
于是 ,
同理 。
于是 。
那么 故答案为:60
【分析】连接 、,根据BE,BF和AB,BC的关系得到三角形BEF和三角形ABC的面积关系,同理可以得出三角形HDG和三角形ADC的面积关系,根据这些关系可以得出它们和四边形ABCD的面积关系,用相同的方法可以得出四边形ABCD和三角形AEH,CFG,ABD,CBD的关系,综合他们的关系以及已知条件,即可解出四边形EFGH的面积
21.【答案】0.86
【解析】【解答】解:1+1=2(cm),
2×2-3.14×1
=4-3.14
=0.86(cm )
故答案为:0.86。
【分析】不能达到的部分实际就是四个角的部分,这四部分的面积实际就是边长2厘米的正方形面积减去一个半径1厘米的圆面积。
22.【答案】(1)10
(2)解:长方形的长画5厘米,宽画3厘米,面积就是15平方厘米,
【解析】【解答】解:(1)涂色部分有10格,图中涂色部分的面积是10平方厘米。
故答案为:(1)10。
【分析】(1)涂色部分下面的三角形,通过观察有2个小正方形,据此解答;
(2)长方形的面积=长×宽,据此作图。
23.【答案】解:8×5=40(平方米)
(8-1)×(5-1.8)÷2 =11.2(平方米)
(40-11.2)×2.5 = 72(千克)
答: 粉刷这面墙至少要用72千克涂料。
【解析】【分析】如图:,墙的面积=长方形的面积-三角形的面积,长方形的面积=长×宽,三角形的面积=底×高÷2,然后用墙的面积乘每平方米用涂料的重量,据此解答。
24.【答案】解:(70+140)×240÷2 =25200(m2)
150×200÷2=15000(m2)
25200+15000=40200(m2)
40200m2=4.02公顷
答:这个草场的占地面积是4.02公顷。
【解析】【分析】如图,,草场的占地面积=梯形面积+三角形面积,梯形的面积=(上底+下底)×高÷2,三角形的面积=底×高÷2,据此解答。
25.【答案】解:根据题意,可得
(16-2)×(8-2)÷4
=14×6÷4
=84÷4
=21(平方米)
答:每一块地的面积是21平方米.
【解析】【分析】通过平移把四块菜地转化为:长是(16-2)米,宽是(8-2)米,根据长方形的面积公式:s=ab,把数据代入公式求出总面积,然后除以4即可.
26.【答案】解:半径: 4÷2 =2(厘米)
(平方厘米)
答:图中阴影部分的面积是3.44平方厘米。
【解析】【分析】观察图形,半圆的直径是4厘米,根据直径=半径×2,可以得到半圆的半径就是4÷2 =2(厘米),然后根据圆的面积公式:S=πr2,代入数据求出圆的面积,又已知正方形的边长是4厘米,根据正方形的面积公式:S=边长×边长,计算得出正方形的面积,最后用正方形的面积减去圆的面积,即可得到阴影部分的面积。
27.【答案】解:半径: 40÷2 =20(米)
面积:
一圈长: 100×2+3.14×40=325.6(m)
答:学校操场的面积是5256平方米,沿这个操场的边线跑一圈有325.6米长。
【解析】【分析】观察图形,学校操场的占地面积就是直径为40米的圆的面积加上长100米,宽40米长方形的面积;根据圆的半径=直径2,计算得到圆的半径是40÷2 =20(米),然后根据长方形的面积公式:S=长×宽,圆的面积公式:S=πr2,代入数据计算即可得到这个操场的占地面积;沿这个操场的边线跑一圈的长度就是直径为40米的圆的周长加上两条100米的长度,根据圆的周长公式:C=πd,代入数据计算即可。
28.【答案】(1)解:17×7+13×7
=119+91
=210(平方米)
答:这块菜地的面积是210平方米。
(2)解:7+13=20(米)
(20+17)×2
=37×2
=74(米)
答:要用74米长的篱笆。
【解析】【分析】(1)这块菜地的面积=左边长方形的面积+右边长方形的面积;其中,长方形的面积=长×宽;
(2)利用平移的方法,把这个图形的边经过平移变成长方形,要用篱笆的长度=长方形的周长=(长+宽)×2。
29.【答案】解:(12+25)×16÷2-16×1
=296-16
=280(m2)
答:草地的面积是280平方米。
【解析】【分析】草地的面积=(整个梯形的上底+下底)×高÷2-中间小路的长×宽。
30.【答案】解:如图所示,作出辅助线,
阴影部分的面积=10×10﹣(10×10﹣3×2)÷2,
=100﹣(100﹣6)÷2,
=100﹣94÷2,
=100﹣47,
=53(平方米);
答:花圃的面积是53平方米.
【解析】【分析】由题意可知:四个角就是四个直角三角形;我们可以把它画成4个长方形,最后就有一个黑色长方形,把整个正方形的面积减去黑色部分长方形的面积再除于2就是四个直角三角形的面积总和,进而用正方形的面积减去四个直角三角形的面积总和,就是花圃的面积.解答此题的关键是将阴影部分进行分割,进而转化成容易面积的图形,问题得解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
