浙江省永嘉中学2026届高三上学期Z20开学考试物理试卷(含答案)
文档属性
| 名称 | 浙江省永嘉中学2026届高三上学期Z20开学考试物理试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-08-16 15:34:46 | ||
图片预览


文档简介
参考答案及部分题目解析 2025.8
一.单项选择题部分(本题共 10 小题,每小题 3 分,共计 30 分,每题有且仅有一个备选项符合题意,仅选择正
确得分):
10
D
二.不定项选择题部分(本题共 3 小题,每小题 4 分,共计 12 分,每题至少有一个选项符合题意,全选对得 4 分,
选对但补全得 2 分):
三.非选择题部分(本题共 5 小题,共计 58 分):
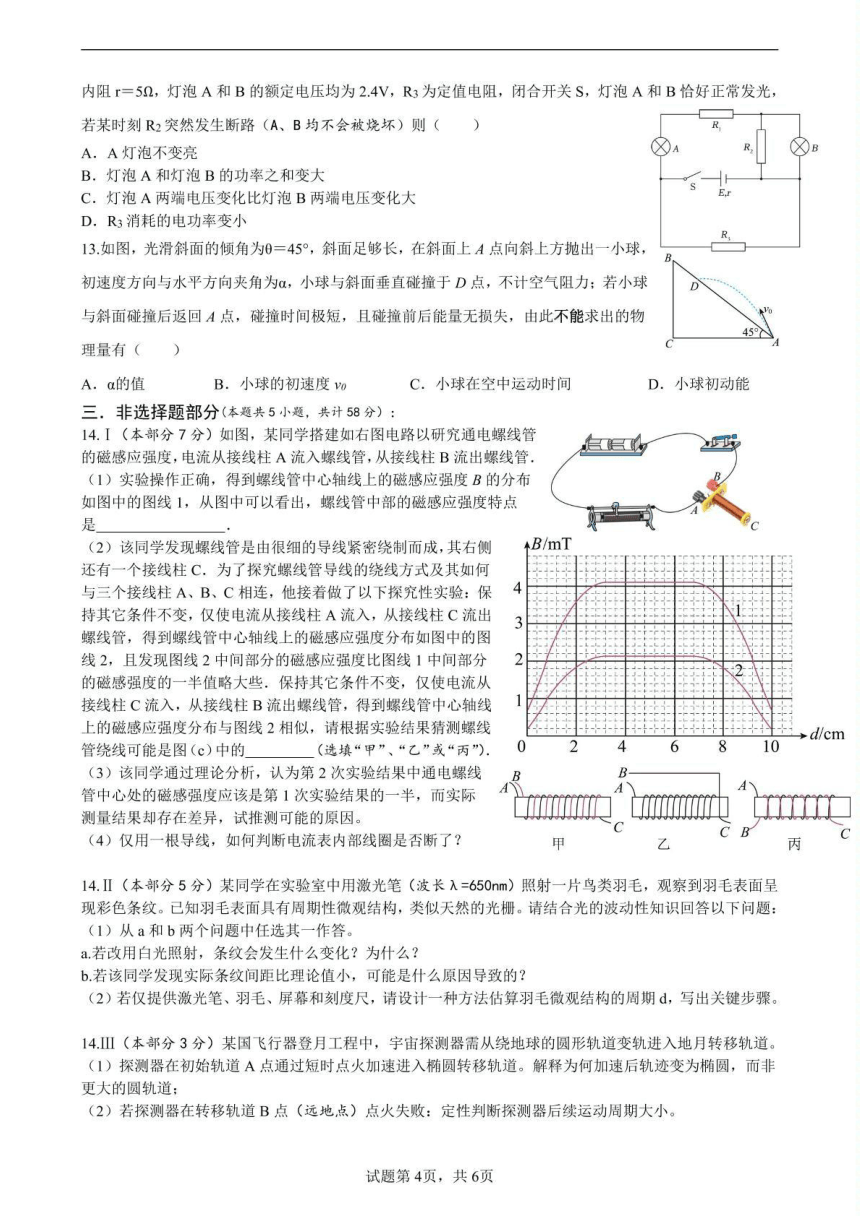
14.Ⅰ(本部分 7 分)匀强磁场(1 分) 丙 螺线管导线存在电阻
短接电流表前后各摇动电流表一次,比较指针偏转,有明显变化,则线圈断了,反之则未断 14.Ⅱ(本部分 5 分)(1)a 改用白光时:
中央条纹为白色,因所有波长的光在该位置光程差为零,干涉相长;其他级次条纹会因不同
波长光的衍射角差异而 色散成彩虹状(如红光在外侧,紫光在内侧);高级次条纹因不同颜色重叠而模糊甚至消失(2 分)
b 条纹间距异常的可能原因:周期 d 的测量误差:若实际周期 d 小于理论值,条纹间距会变小;斜入射影响:若激光未垂直入射光栅,光程差公式需修正,导致条纹位置偏移;羽毛结 构非理想:实际结构可能存在不均匀性或非严格周期性,导致衍射效率降低。(2 分)
(2)实验设计步骤与公式:
固定激光笔与羽毛,使激光垂直照射羽毛,并在后方距离 L 处放置屏幕;
测量屏幕上第 k 级亮纹与中央亮纹的间距 x ,由小角度近似 d≈
改变 k 多次测量取平均值,提高精度。(3 分)
14.Ⅲ(本部分 3 分)(1)短时点火使探测器速度突增,但未持续推力,此时动能增加导致机械能大于原圆轨道机械能,但新轨道仍为闭合曲线,故变为椭圆。
(2)点火失败后,探测器沿原转移轨道继续绕地球运行,周期不变。(1 分)选择题解析:
粒子与 Rn 核,动量守恒与能量守恒有
,
卫星在低轨时的动能为 ,卫星在低轨时的势能为卫星在高轨时的动能为 ,卫星在高轨时的势能为 令卫星在 Q 处加速过程发动机做的功为 ,根据动能定理有
,当增大 M 值后 会减小,小球和半圆形凹槽在水平方向的动能
会减小。半圆形凹槽竖直方向没有速度,则小球在竖直方向的速度一定增加,小球会飞的更高,故 B 正确。
F= 当
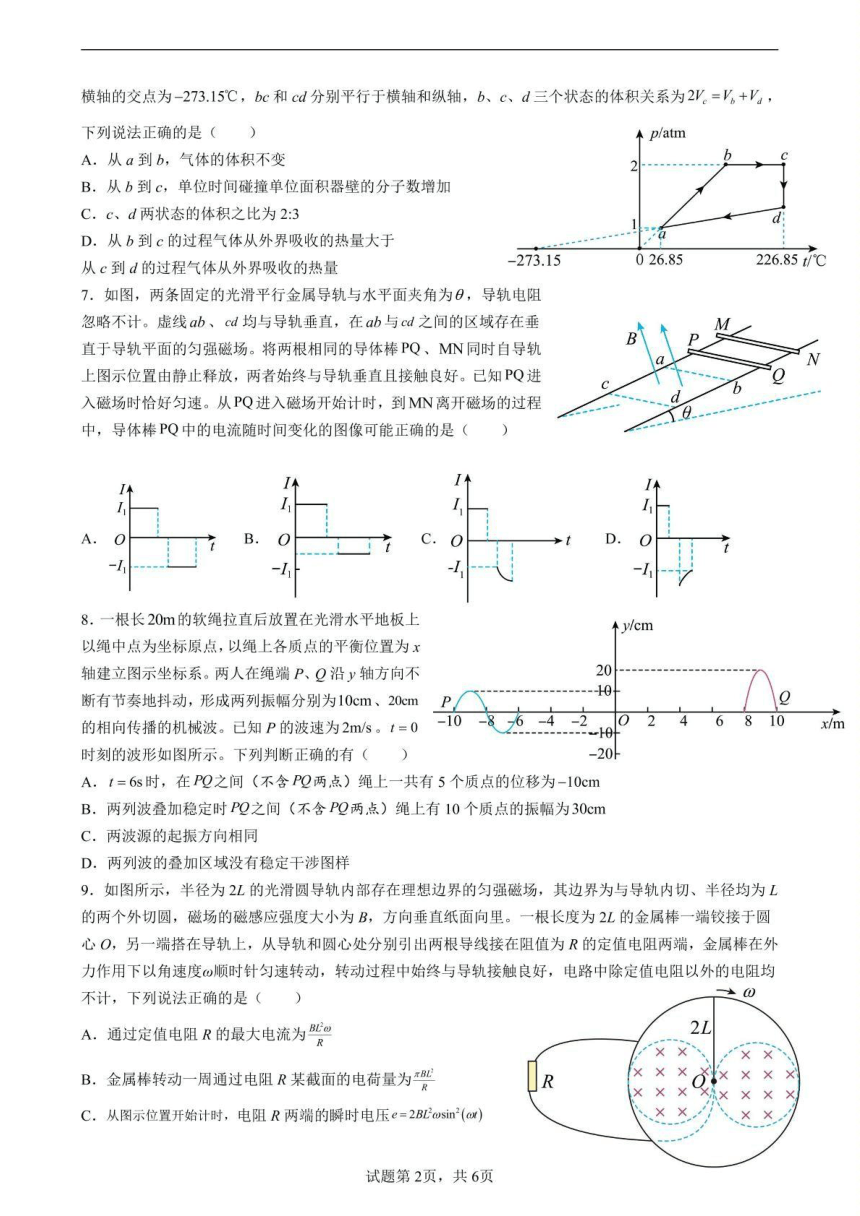
6.D.由 , 联立解得 bcd 过程的 如图
由图可知,b 到 c 和 c 到 d 的体积差相等。由于 图线与横坐标围成的面积表示气体对外界做的功,显然 b 到 c,气体温度升高,内能增加,根据热力学第一定律得
c 到 d,气体温度不变,内能不变,根据热力学第一定律得 联立可得
7.设导轨宽度为 L,回路电阻为 R,PQ 进入磁场时速度为 ,MN 进入磁场时速度为 ,
易判断 ,已知 进入磁场时恰好匀速,则有安培力等于 ,回路电流 情
况 1:若 PQ 出磁场时,MN 未进入磁场,则当 PQ 匀速出磁场过程,电流 不变,右手定则可知电流方向为 Q 指向 P,之后当 MN 进入磁场时,回路电流 右手定则可知,电
流方向 P 到 Q,因为 ,所以有 ,分析可知 MN 棒做减速运动,即 会逐渐减小到可能等于 的过程;情况 2:若 PQ 出磁场前,MN 已进入磁场,则此时回路电流
楞次定律可知电流方向为 P 到 Q,由于不知道 具体大小,故可能此时
有 ,则有 ,之后 MN 减速,PQ 加速,即 减小, 减小.
8.A.有 5 个点位移为-10cmB.在叠加稳定时两波源间(不含波源)有 9 个质点的振幅为
30cm。C.P 起振方向沿 y 轴负方向,而 Q 起振方向沿 y 轴正方向,因此起振方向相反,C错误;D.两列波的频率均
为 0.5Hz,叠加区域有稳定干涉图样,D 错误。
9.B.在t 时间内回路中磁通量的变化量对应如图甲所示的阴影部分,则金属棒转动一周回路中磁通量的变化量为 ,通过回路某截面的电荷量为 CD.从图示位置开始计时,t 时刻金属棒转过的角度为 结合如图乙所示的几何关系,回路中产生的感应电动势 通过电阻 R 的瞬时电流 .
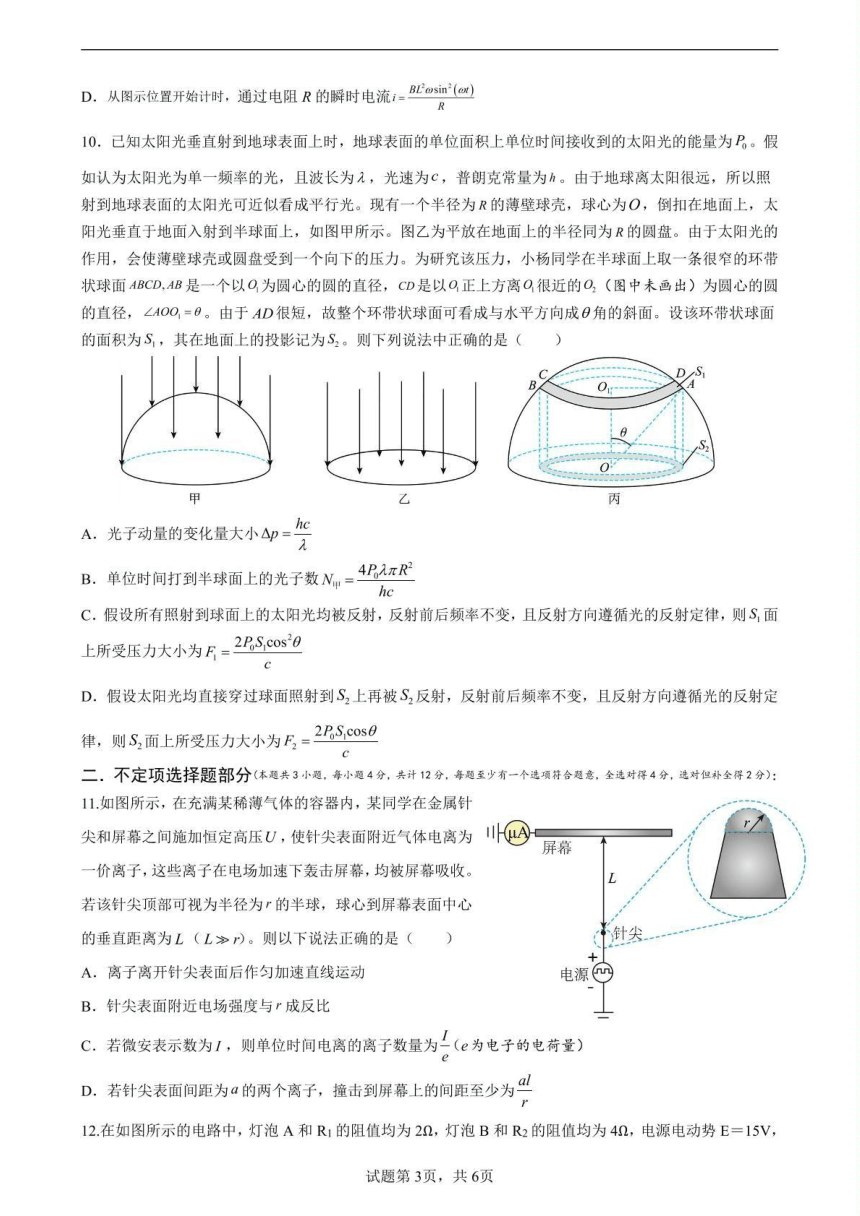
10.A.若光被反射,反射前后频率不变,则 方向垂直于 S1 面.B.单位时间打
到半球面上的光子数 C.在 时间内,射到 S1 面上的光子数为 光子被全部反射,光子受到的力大小为 F10,
, S1 面受到的力大小为
D.在时间内,射到 S2 面上的光子数为 太阳光直接穿过球面照射到 S2 上再被 S2 反射,反射前后频率不变 根据动量定理,光子受到的力大小为
得 由于
根据牛顿第三定律,S2 面受到的力大小为
12. C、因为灯泡 A 和 B 电压之和增大,而灯泡 A 两端电压减小,则灯泡 B 两端电压增大,并且灯泡 B 两端电压变化的值大于灯泡 A 两端电压变化的值,故 C 错误;D、由于 R3 两端电压变大,所以 R3 消耗功率变大,故 D 错误。
解答题
15.(1)(3 分)初始状态玻璃管内气体的压强和体积分别为
末状态玻璃管内气体的压强和体积分别为
玻璃管内的气体做等温变化,由玻意耳定律得 求得
(2)(4 分)初始气缸内气体的压强和体积分别为 末状态压强和体积分别为由玻意耳定律得 求得
16.(1()3 分)物块以一定的初速度沿轨道恰好运动到 点,设物块到达 点的速度为 ,则有
根据机械能守恒可得 联立解得物块在 点的速度大小为
(2()4 分)根据图像可知,当 时,物块与轨道相对静止,加速度根据图 像斜率可知 当 时,物块与轨道相对运动,物块加速度 根据图像斜率可知 可得 轨道加速度
(3()4 分) 时,则物块与轨道相对运动,由图可知,物块加速度 轨道加速
度 ;
物块运动到 点所用时间为 ,则物块速度 则轨道速度 设物块沿轨道恰好到达与圆心 O 点等高处时的速度为 ,根据动量守恒有 根据能量守恒有
解得 物块运动到 点过程
中位移为 此过程中轨道位移为 轨道水平部分长度为 由于 、质量相等,再次回到 B 点时交换速度, , 物块再加速,轨道再减速,
最终达到共同速度 则有 解得 解得从 B 点开始,物块对地
, 可知 说明物块恰好停在轨道的 A 处。 17.(1)(4 分)运动的导体棒充当电源,则 导体棒切割磁感线 根据题意可知,在 时刻导体棒恰好运动到 处时 ,此时
(2()4 分)回复力与偏离平衡位置的距离成正比,由图像可知到 点为平衡位置,根据动能定理 又根据 , 联立得 金属棒产生的焦耳热为
(3()4 分)在 到 范围内,安培力大小为 可知安培力随位置线性变化,即 代入数据得 在 处,导体棒速度为
根据动能定理可知 又因为 , 解得 对全过程
列动能定理,有
故金属棒从 运动到 过程中外力的平均功率为
18.(1()4 分)粒子在磁场中做匀速圆周运动,由洛伦兹力提供向心力,则有 解得
粒子在磁场中运动的周期为 Q 点入射弦切角为 ,有弦 所对圆心角为 ,弦长等于半径 所以粒子在磁场中做圆周运动,轨迹对应的圆心角为
则粒子第一次在磁场中运动的时间
(2()5 分)因为 则 与弦切角相等,故粒子沿 x 轴正方向出磁场,匀速经无场区后,进入电场做类平抛运动, 方向有 由几何关系可知
立解得
方向有 由几何关系可知 联
(3()4 分)粒子在电场中类平抛到 Q 点速度 与 x 轴的夹角始终为 ,则 又由(1)得 其中 解得 第 n 次在磁场中运动的时间为 其 中 故第 n 次在磁场中运动的时间为 第 n 次在无场区和电场中的类平抛,x 轴方向保持匀速运动,由第 n 次在无场区和电场中的时间为
其中 故第 n 次在无场区和电场中的时间为 所以粒
子第 n 次从 Q 进入磁场再回 Q 点的时间
一.单项选择题部分(本题共 10 小题,每小题 3 分,共计 30 分,每题有且仅有一个备选项符合题意,仅选择正
确得分):
10
D
二.不定项选择题部分(本题共 3 小题,每小题 4 分,共计 12 分,每题至少有一个选项符合题意,全选对得 4 分,
选对但补全得 2 分):
三.非选择题部分(本题共 5 小题,共计 58 分):
14.Ⅰ(本部分 7 分)匀强磁场(1 分) 丙 螺线管导线存在电阻
短接电流表前后各摇动电流表一次,比较指针偏转,有明显变化,则线圈断了,反之则未断 14.Ⅱ(本部分 5 分)(1)a 改用白光时:
中央条纹为白色,因所有波长的光在该位置光程差为零,干涉相长;其他级次条纹会因不同
波长光的衍射角差异而 色散成彩虹状(如红光在外侧,紫光在内侧);高级次条纹因不同颜色重叠而模糊甚至消失(2 分)
b 条纹间距异常的可能原因:周期 d 的测量误差:若实际周期 d 小于理论值,条纹间距会变小;斜入射影响:若激光未垂直入射光栅,光程差公式需修正,导致条纹位置偏移;羽毛结 构非理想:实际结构可能存在不均匀性或非严格周期性,导致衍射效率降低。(2 分)
(2)实验设计步骤与公式:
固定激光笔与羽毛,使激光垂直照射羽毛,并在后方距离 L 处放置屏幕;
测量屏幕上第 k 级亮纹与中央亮纹的间距 x ,由小角度近似 d≈
改变 k 多次测量取平均值,提高精度。(3 分)
14.Ⅲ(本部分 3 分)(1)短时点火使探测器速度突增,但未持续推力,此时动能增加导致机械能大于原圆轨道机械能,但新轨道仍为闭合曲线,故变为椭圆。
(2)点火失败后,探测器沿原转移轨道继续绕地球运行,周期不变。(1 分)选择题解析:
粒子与 Rn 核,动量守恒与能量守恒有
,
卫星在低轨时的动能为 ,卫星在低轨时的势能为卫星在高轨时的动能为 ,卫星在高轨时的势能为 令卫星在 Q 处加速过程发动机做的功为 ,根据动能定理有
,当增大 M 值后 会减小,小球和半圆形凹槽在水平方向的动能
会减小。半圆形凹槽竖直方向没有速度,则小球在竖直方向的速度一定增加,小球会飞的更高,故 B 正确。
F= 当
6.D.由 , 联立解得 bcd 过程的 如图
由图可知,b 到 c 和 c 到 d 的体积差相等。由于 图线与横坐标围成的面积表示气体对外界做的功,显然 b 到 c,气体温度升高,内能增加,根据热力学第一定律得
c 到 d,气体温度不变,内能不变,根据热力学第一定律得 联立可得
7.设导轨宽度为 L,回路电阻为 R,PQ 进入磁场时速度为 ,MN 进入磁场时速度为 ,
易判断 ,已知 进入磁场时恰好匀速,则有安培力等于 ,回路电流 情
况 1:若 PQ 出磁场时,MN 未进入磁场,则当 PQ 匀速出磁场过程,电流 不变,右手定则可知电流方向为 Q 指向 P,之后当 MN 进入磁场时,回路电流 右手定则可知,电
流方向 P 到 Q,因为 ,所以有 ,分析可知 MN 棒做减速运动,即 会逐渐减小到可能等于 的过程;情况 2:若 PQ 出磁场前,MN 已进入磁场,则此时回路电流
楞次定律可知电流方向为 P 到 Q,由于不知道 具体大小,故可能此时
有 ,则有 ,之后 MN 减速,PQ 加速,即 减小, 减小.
8.A.有 5 个点位移为-10cmB.在叠加稳定时两波源间(不含波源)有 9 个质点的振幅为
30cm。C.P 起振方向沿 y 轴负方向,而 Q 起振方向沿 y 轴正方向,因此起振方向相反,C错误;D.两列波的频率均
为 0.5Hz,叠加区域有稳定干涉图样,D 错误。
9.B.在t 时间内回路中磁通量的变化量对应如图甲所示的阴影部分,则金属棒转动一周回路中磁通量的变化量为 ,通过回路某截面的电荷量为 CD.从图示位置开始计时,t 时刻金属棒转过的角度为 结合如图乙所示的几何关系,回路中产生的感应电动势 通过电阻 R 的瞬时电流 .
10.A.若光被反射,反射前后频率不变,则 方向垂直于 S1 面.B.单位时间打
到半球面上的光子数 C.在 时间内,射到 S1 面上的光子数为 光子被全部反射,光子受到的力大小为 F10,
, S1 面受到的力大小为
D.在时间内,射到 S2 面上的光子数为 太阳光直接穿过球面照射到 S2 上再被 S2 反射,反射前后频率不变 根据动量定理,光子受到的力大小为
得 由于
根据牛顿第三定律,S2 面受到的力大小为
12. C、因为灯泡 A 和 B 电压之和增大,而灯泡 A 两端电压减小,则灯泡 B 两端电压增大,并且灯泡 B 两端电压变化的值大于灯泡 A 两端电压变化的值,故 C 错误;D、由于 R3 两端电压变大,所以 R3 消耗功率变大,故 D 错误。
解答题
15.(1)(3 分)初始状态玻璃管内气体的压强和体积分别为
末状态玻璃管内气体的压强和体积分别为
玻璃管内的气体做等温变化,由玻意耳定律得 求得
(2)(4 分)初始气缸内气体的压强和体积分别为 末状态压强和体积分别为由玻意耳定律得 求得
16.(1()3 分)物块以一定的初速度沿轨道恰好运动到 点,设物块到达 点的速度为 ,则有
根据机械能守恒可得 联立解得物块在 点的速度大小为
(2()4 分)根据图像可知,当 时,物块与轨道相对静止,加速度根据图 像斜率可知 当 时,物块与轨道相对运动,物块加速度 根据图像斜率可知 可得 轨道加速度
(3()4 分) 时,则物块与轨道相对运动,由图可知,物块加速度 轨道加速
度 ;
物块运动到 点所用时间为 ,则物块速度 则轨道速度 设物块沿轨道恰好到达与圆心 O 点等高处时的速度为 ,根据动量守恒有 根据能量守恒有
解得 物块运动到 点过程
中位移为 此过程中轨道位移为 轨道水平部分长度为 由于 、质量相等,再次回到 B 点时交换速度, , 物块再加速,轨道再减速,
最终达到共同速度 则有 解得 解得从 B 点开始,物块对地
, 可知 说明物块恰好停在轨道的 A 处。 17.(1)(4 分)运动的导体棒充当电源,则 导体棒切割磁感线 根据题意可知,在 时刻导体棒恰好运动到 处时 ,此时
(2()4 分)回复力与偏离平衡位置的距离成正比,由图像可知到 点为平衡位置,根据动能定理 又根据 , 联立得 金属棒产生的焦耳热为
(3()4 分)在 到 范围内,安培力大小为 可知安培力随位置线性变化,即 代入数据得 在 处,导体棒速度为
根据动能定理可知 又因为 , 解得 对全过程
列动能定理,有
故金属棒从 运动到 过程中外力的平均功率为
18.(1()4 分)粒子在磁场中做匀速圆周运动,由洛伦兹力提供向心力,则有 解得
粒子在磁场中运动的周期为 Q 点入射弦切角为 ,有弦 所对圆心角为 ,弦长等于半径 所以粒子在磁场中做圆周运动,轨迹对应的圆心角为
则粒子第一次在磁场中运动的时间
(2()5 分)因为 则 与弦切角相等,故粒子沿 x 轴正方向出磁场,匀速经无场区后,进入电场做类平抛运动, 方向有 由几何关系可知
立解得
方向有 由几何关系可知 联
(3()4 分)粒子在电场中类平抛到 Q 点速度 与 x 轴的夹角始终为 ,则 又由(1)得 其中 解得 第 n 次在磁场中运动的时间为 其 中 故第 n 次在磁场中运动的时间为 第 n 次在无场区和电场中的类平抛,x 轴方向保持匀速运动,由第 n 次在无场区和电场中的时间为
其中 故第 n 次在无场区和电场中的时间为 所以粒
子第 n 次从 Q 进入磁场再回 Q 点的时间
同课章节目录
