(小升初开学分班考)小升初开学重点校分班摸底预测卷-2025年秋六年级数学西师大版(含答案解析)
文档属性
| 名称 | (小升初开学分班考)小升初开学重点校分班摸底预测卷-2025年秋六年级数学西师大版(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 193.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-16 12:28:23 | ||
图片预览



文档简介
/ 让学习更有效 小升初备考 | 数学学科
2025年秋六年级数学小升初开学重点校分班摸底预测卷(西师大版)
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题(共10小题)
1.一辆自行车,行驶中后齿轮转24圈,前齿轮转14圈,则前齿轮和后齿轮的齿数最简比( )
A.12:7 B.14:24 C.7:12 D.24:14
2.一种运动鞋,在“6.18网购节”时,先提价20%后又打八折,与原价相比,现价( )
A.降低了 B.提高了 C.不变 D.无法确定
3.如图所示,把底面直径是8cm的圆柱切成若干等份,拼成一个近似的长方体,这个长方体的表面积比原来增加了80cm2,那么长方体的体积是( )cm3。
A.251.2 B.502.4 C.2009.6 D.1004.8
4.下列说法错误的有( )项。
①把一个圆柱的侧面剪开,不可能得到平行四边形。
②平行四边形的面积一定,它的底和对应的高成反比例。
③实际距离一定比相对应的图上距离大。
④一个长方形面积一定时,它的长与宽的关系用图像表示出来是一条直线。
A.1 B.2 C.3 D.4
5.现在从甲、乙、丙、丁四个人中选出两个人参加一项活动。规定:如果甲去,那么乙也去;如果丙不去,那么乙也不去;如果丙去;那么丁不去。最后去参加活动的两个人是( )
A.甲、乙 B.甲、丙 C.乙、丙 D.乙、丁
6.甲从A地出发向B地,同时,乙、丙两人从B地驾车出发,向A地行驶,甲、乙两人相遇在离A地3千米的C地,乙到A地后立即掉头,与丙在C地相遇,若开始出发时甲就跑步,速度提高到步行速度的2.5倍,则甲、丙相遇地点距A地7.5 千米,A、B两地距离( )千米。
A.21 B.22.5 C.24 D.25.5
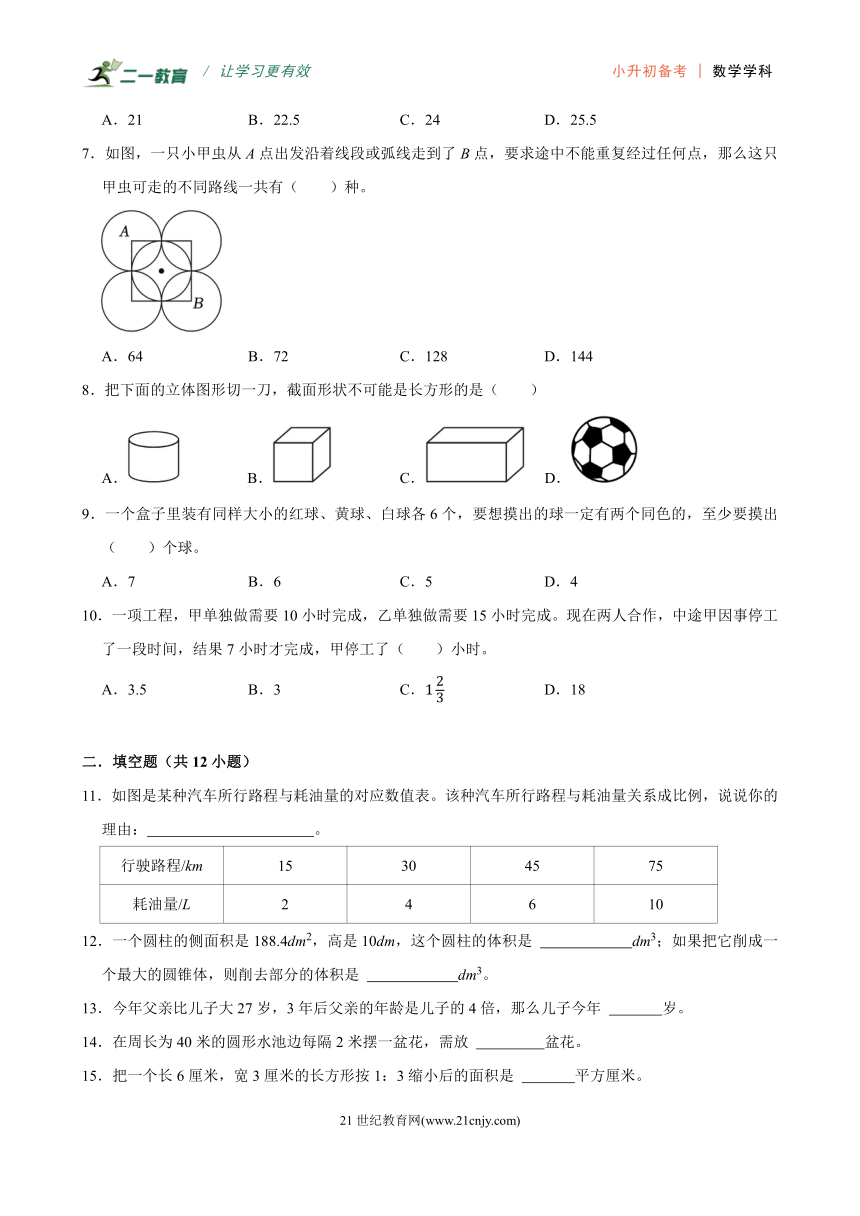
7.如图,一只小甲虫从A点出发沿着线段或弧线走到了B点,要求途中不能重复经过任何点,那么这只甲虫可走的不同路线一共有( )种。
A.64 B.72 C.128 D.144
8.把下面的立体图形切一刀,截面形状不可能是长方形的是( )
A. B. C. D.
9.一个盒子里装有同样大小的红球、黄球、白球各6个,要想摸出的球一定有两个同色的,至少要摸出( )个球。
A.7 B.6 C.5 D.4
10.一项工程,甲单独做需要10小时完成,乙单独做需要15小时完成。现在两人合作,中途甲因事停工了一段时间,结果7小时才完成,甲停工了( )小时。
A.3.5 B.3 C. D.18
二.填空题(共12小题)
11.如图是某种汽车所行路程与耗油量的对应数值表。该种汽车所行路程与耗油量关系成比例,说说你的理由: 。
行驶路程/km 15 30 45 75
耗油量/L 2 4 6 10
12.一个圆柱的侧面积是188.4dm2,高是10dm,这个圆柱的体积是 dm3;如果把它削成一个最大的圆锥体,则削去部分的体积是 dm3。
13.今年父亲比儿子大27岁,3年后父亲的年龄是儿子的4倍,那么儿子今年 岁。
14.在周长为40米的圆形水池边每隔2米摆一盆花,需放 盆花。
15.把一个长6厘米,宽3厘米的长方形按1:3缩小后的面积是 平方厘米。
16.在比例尺是1:4000000的地图上,量得A、B两港距离为9厘米,一艘货轮以每小时24千米的速度从A开向B港,到达B港需要 小时。
17.在20张同样的卡片上分别写上1~20各数,将卡片打乱,从中任意抽取一张,抽到质数的可能性是 。
18.把两个自然数A和B分解质因数:A=2×n×7,B=5×n×7,已知A和B的最小公倍数是210,则两数的最大公约数是 。
19.甲乙两桶油重量差为9千克,甲桶油重量的等于乙桶油重量的,则乙桶油重 千克.
20.一个工厂改革后人员减少20%,产量比原来增加20%,每人工作效率提高 %.
21.甲、乙、丙三人各有一些糖;如果甲的糖数变为原来一半。乙给丙18颗,那么三人的糖数一样多;如果丙的糖数变为原来的2倍,甲给乙一些糖,三人的糖数也能一样多,那么甲给了乙 颗糖。
22.在如图所示的图案中,共可以找到5种不同大小的正方形。若其中较小的四种正方形的边长恰好是四个连续整数(单位:厘米),则其中最大的正方形的周长为 厘米。
三.判断题(共6小题)
23.一种菜籽的出油率达到了120%。
24.0既不是正数也不是负数. .
25.小华家栽了99棵树,活了99棵,成活率是99%.
26.用一副三角板可以拼出一个80°的角。
27.一台电视机提价20%后,又降价20%,价格不变。
28.把18写成质数相乘的形式:18=1×2×3×3。
四.计算题(共3小题)
29.直接写出得数。
1.2×0.4= 53+4.7= 3.2÷0.04= 3
30.解方程。
24x+7=127 2.1+0.7x=5.6
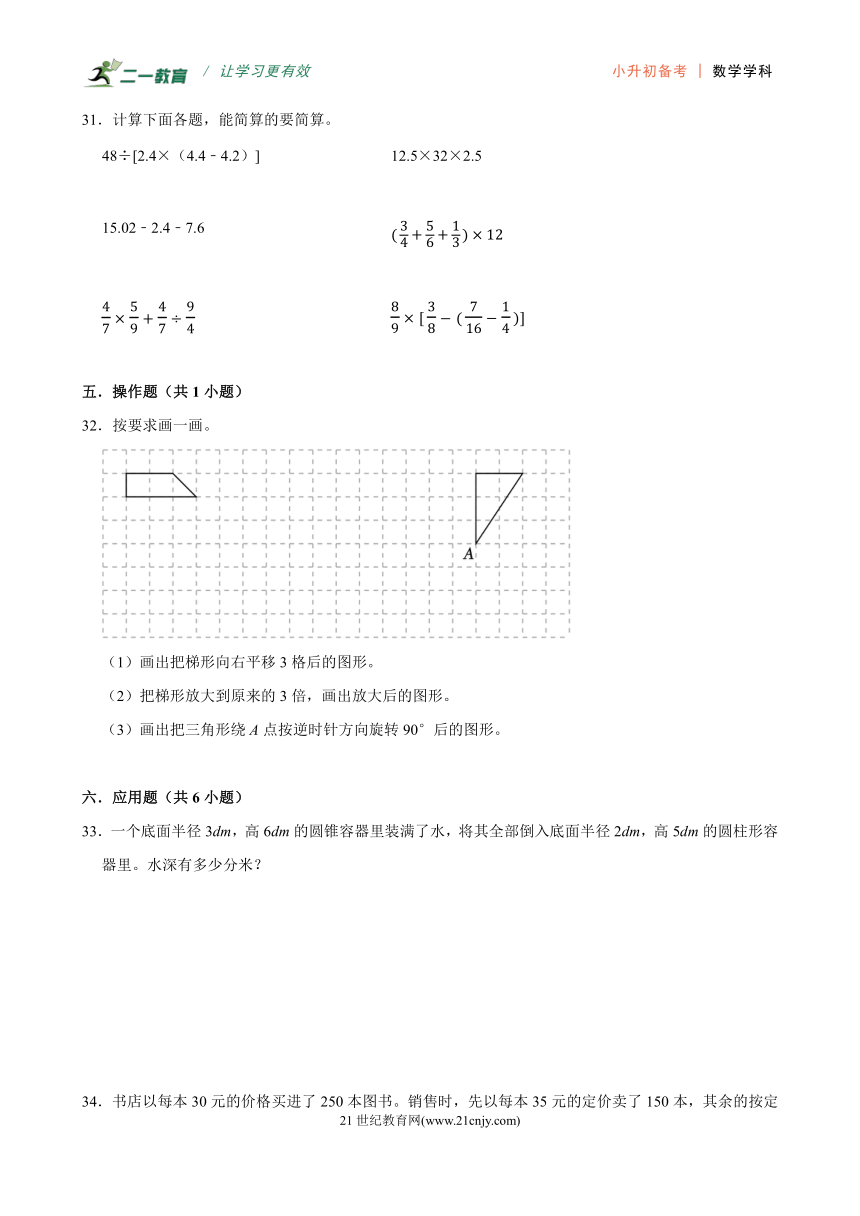
31.计算下面各题,能简算的要简算。
48÷[2.4×(4.4﹣4.2)] 12.5×32×2.5
15.02﹣2.4﹣7.6
五.操作题(共1小题)
32.按要求画一画。
(1)画出把梯形向右平移3格后的图形。
(2)把梯形放大到原来的3倍,画出放大后的图形。
(3)画出把三角形绕A点按逆时针方向旋转90°后的图形。
六.应用题(共6小题)
33.一个底面半径3dm,高6dm的圆锥容器里装满了水,将其全部倒入底面半径2dm,高5dm的圆柱形容器里。水深有多少分米?
34.书店以每本30元的价格买进了250本图书。销售时,先以每本35元的定价卖了150本,其余的按定价的八折全部卖完。这个商店赚了(或亏了)多少元?
35.甲、乙两辆汽车分别同时从A、B两地相对开出,甲车每小时行驶50千米,乙车每小时行驶40千米,经过4小时两车共行了全程的80%。当甲车到达B地时,乙车离A地还有多少千米?
36.有两张长18.84dm,宽12.56dm的铁皮,一张顺着长(长为高)卷成一个最大的圆柱A,一张顺着宽(宽为高)卷成一个最大的圆柱B,分别给两个圆柱焊上一个底面。哪个圆柱的表面积大些?大多少平方分米?
37.高新区综合办公大楼原来平均每天照明用电80千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来30天的用电量现在可以用多少天?
38.北京轨道交通里程大约528km,重庆轨道交通里程约占北京的。近十年重庆轨道交通快速发展,到2024年初重庆轨道交通里程是2015年的2.69倍,约占同时期北京轨道交通里程的64.3%。2024年初,重庆轨道交通里程是多少千米?
参考答案及试题解析
一.选择题(共10小题)
1.【考点】比的意义.
【答案】A
【思路分析】根据题意可知:前、后齿轮走过的路程是相同的,也就是齿轮的齿数×转动的圈数=走过的路程(一定),所以齿数与转的圈数乘反比例,据此解答即可。
【解答】解:设前齿轮和后齿轮的齿数分别是x、y。
14x=24y
x:y=24:14=12:7
答:前齿轮和后齿轮的齿数最简比是12:7。
故选:A。
【名师点评】知道齿轮的齿数×转动的圈数=走过的路程(一定),是解答此题的关键。
2.【考点】百分数的实际应用.
【答案】A
【思路分析】把原价看作单位“1”,提价20%后,价格为原价的(1+20%),又打八折价格为原价的(1+20%)×80%,据此解答。
【解答】解:1×(1+20%)×80%
=120%×80%
=96%
即现在的价格是原价的96%,所以现在的价格降了。
答:现在的价格降了。
故选:A。
【名师点评】本题主要考查百分数的实际应用,把原价看作单位“1”,是解答关键。
3.【考点】圆柱的侧面积、表面积和体积.
【答案】B
【思路分析】根据圆柱体积公式的推导过程可知,把一个圆柱切拼成一个近似长方体,体积不变。拼成的长方体的表面积比圆柱的表面积增加了两个切面的面积,每个切面的长等于圆柱的高,每个切面的宽等于圆柱的底面半径,根据长方形的面积公式:S=ab,把数据代入公式求出圆柱的高,然后根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:80÷2÷(8÷2)
=40÷4
=10(厘米)
3.14×(8÷2)2×10
=3.14×16×10
=50.24×10
=502.4(立方厘米)
答:长方体的体积是502.4立方厘米。
故选:B。
【名师点评】此题考查的目的是理解掌握圆柱体积公式的推导过程及应用,长方形的面积公式及应用,关键是熟记公式。
4.【考点】辨识成正比例的量与成反比例的量;圆柱的展开图.
【答案】C
【思路分析】根据辨识成正比例的量与成反比例的量的方法以及比例尺的意义、圆柱的展开图知识,分析解答即可。
【解答】解:①把一个圆柱的侧面剪开,可能得到长方形、正方形或平行四边形,所以本选项说法错误;
②平行四边形的面积一定,是乘积一定,所以底和对应的高成反比例,所以本选项说法正确;
③当实际距离比较大时,所画的图上距离要比实际距离小,当实际长度较小时,如手表等精密零件,所画的图上距离要比实际距离大,因此,实际距离一定比相对应的图上距离要大这种说法是错误的;
④一个长方形面积一定时,是乘积一定,它的长与宽的关系是反比例关系,用图像表示出来不是一条直线。所以本选项说法错误。
故选:C。
【名师点评】本题考查了辨识成正比例的量与成反比例的量的方法以及比例尺的意义、圆柱的展开图知识,结合题意分析解答即可。
5.【考点】逻辑推理;盈亏问题.
【答案】C
【思路分析】①根据如果甲去,那么乙也去,可得甲去,乙必然也去;②又根据如果丙不去,那么乙也不去,可得如果乙去了,丙也一定去了,同时满足①②的条件和“如果丙去;那么丁不去”只能是乙、丙参加了活动,据此解答即可。
【解答】解:根据如果甲去,那么乙也去,可得甲去,乙必然也去,又根据如果丙不去,那么乙也不去,可得如果乙去了,丙也一定去了,如果丙去;那么丁不去,可得:如果丙不去;那么丁去,同时乙也不去,则根据“甲去,那么乙也去”可得甲也不去,这样只有丁去,这与两个人参加一项活动相矛盾。同时满足条件只能是乙、丙参加了活动。
故选:C。
【名师点评】本题的关键是根据如果甲去,那么乙也去;如果丙不去,那么乙也不去的话入手,来进行推理。
6.【考点】相遇问题.
【答案】A
【思路分析】若开始出发时甲就跑步,速度提高到步行速度的2.5倍,则甲原来走3千米,甲提高速度后走的路程就是3×2.5=7.5千米,而这时甲、丙相遇地点距A地7.5千米。可知两次相遇用的时间相同。因两次相遇时的时间相同,所以乙丙二人的速度比是(3+3):(7.5﹣3)=4:3,把第一次相遇时,丙走的路程看作单位“1”,依据时间一定,速度和路程成正比,可得甲走了丙的路程,此时乙比丙多走7.5﹣3=4.5千米,依据分数除法意义,求出丙走的路程,再加上7.5就是A、B两地间的路程。
【解答】解:乙、丙的速度比是:(3+3):(7.5﹣3)=4:3。
(7.5﹣3)÷(1)+7.5
=4.57.5
=13.5+7.5
=21(千米)
答:A、B两地距离21千米。
故选:A。
【名师点评】解答此题的关键是明确提速前甲乙相遇时间和提速后甲丙时间相同。
7.【考点】简单的排列、组合.
【答案】C
【思路分析】
小甲虫想要到B点必须通过交点上C、D、E、F四个点才能到达B;
小虫甲从A到C有4种,从C到D有4种;从D到B有4种;共有4×4×4=64(种);
同理小虫从A通过其他E、F个点到B点也是64种,
所以共有4×4×4×2种。
【解答】解:4×4×4×2
=64×2
=128(种)
答:这只甲虫可走的不同路线一共有128种。
故选:C。
【名师点评】本题考查了乘法原理和加法原理的综合应用,关键是确定每一步有几种走法。
8.【考点】圆柱的特征;长方体的特征;正方体的特征.
【答案】D
【思路分析】用一个平面截一个几何体得到的形状叫做几何体的截面,据此分析解答。
【解答】解:圆柱,正方体,长方体的截面都可能出现长方形,只有球的截面只与圆有关。
故选:D。
【名师点评】本题考查了立体图形截面形状的认识。
9.【考点】抽屉原理.
【答案】D
【思路分析】最坏情况是红球、白球、黄球各摸出1个,此时再摸出1个球,一定有2个同色的,一共需要摸出4个球。
【解答】解:考虑最差情况:摸出2个球,分别是红球、黄球、白球各1个,
那么再任意摸出1个球,一定可以保证有2个球颜色相同,
3+1=4(个)
答:要想摸出的球一定有两个是同色的,至少要摸出4个球。
故选:D。
【名师点评】此题考查了利用抽屉原理解决实际问题的灵活应用,关键是从最差情况考虑。
10.【考点】工程问题.
【答案】C
【思路分析】将工作总量看作单位“1“,设甲停工了 x 小时,根据甲的效率×工作时间+乙的效率×工作时间=1,列出方程,求出x的值即可。
【解答】解:甲的效率:
乙的效率:
设甲停工了 x 小时。
(7﹣x )7=1
x1
1x
x
x=1
答:甲停工了1时。
故选:C。
【名师点评】关键是找到等量关系,理解工作效率、工作时间、工作总量之间的关系,其中时间分之一可以看作效率。
二.填空题(共12小题)
11.【考点】辨识成正比例的量与成反比例的量.
【答案】因为15÷2=30÷4=45÷6=75÷10=7.5,符合正比例关系式x:y=k(一定),所以汽车行驶路程与耗油量是正比例关系。
【思路分析】表中有两种相关联的量,行驶的路程和耗油量,耗油量随着行驶的路程变化而变化,且耗油量与行驶路程的比值是一定的,因为15÷2=30÷4=45÷6=75÷10=7.5,符合正比例关系式x:y=k(一定),所以汽车行驶路程与耗油量是正比例关系,据此解答即可。
【解答】解:该种汽车所行路程与耗油量关系成正比例,因为15÷2=30÷4=45÷6=75÷10=7.5,符合正比例关系式x:y=k(一定),所以汽车行驶路程与耗油量是正比例关系。
故答案为:因为15÷2=30÷4=45÷6=75÷10=7.5,符合正比例关系式x:y=k(一定),所以汽车行驶路程与耗油量是正比例关系。
【名师点评】此题主要考查正比例的意义的实际应用,结合题意分析解答即可。
12.【考点】圆柱的侧面积、表面积和体积;圆锥的体积.
【答案】282.6,188.4。
【思路分析】根据圆柱的侧面积公式:S=2πrh,据此可以求出圆柱的底面半径,再根据圆柱的体积公式:V=πr2h,把数据代入公式求出圆柱的体积,如果把它削成一个最大的圆锥体,则削去部分的体积是圆柱体积的(1),据此解答即可。
【解答】解:188.4÷10÷3.14÷2
=18.84÷3.14÷2
=6÷2
=3(分米)
3.14×32×10
=3.14×9×10
=28.26×10
=282.6(立方分米)
282.6÷3×2
=94.2×2
=188.4(立方分米)
答:这个圆柱的体积是282.6立方分米,如果把它削成一个最大的圆锥体,则削去部分的体积是188.4立方分米。
故答案为:282.6,188.4。
【名师点评】此题主要考查圆柱的侧面积公式、圆柱的体积公式的灵活应用,以及等底等高的圆柱与圆锥体积之间的关系及应用。
13.【考点】年龄问题.
【答案】见试题解答内容
【思路分析】根据年龄差不会随时间的变化而改变,知道3年后父子的年龄差是27岁,由此根据差倍关系求出3年后儿子的年龄,进而求出儿子今年的年龄.
【解答】解:4﹣1=3;
27÷3=9(岁);
9﹣3=6(岁);
答:儿子今年6岁.
故答案为:6.
【名师点评】关键是根据年龄差不会随时间的变化而改变,利用差倍公式{差÷(倍数﹣1)=小数,小数×倍数=大数,(或 小数+差=大数)解决问题.
14.【考点】植树问题.
【答案】20。
【思路分析】围成圆圈摆放花盆,花盆数=间隔数,由此求出40米里有几个2米的间隔,就有几盆花。
【解答】解:40÷2=20(盆)
答:需放20盆花。
故答案为:20。
【名师点评】此题属于围成圆圈植树问题,植树棵数=间隔数。
15.【考点】图形的放大与缩小.
【答案】2。
【思路分析】长方形按1:3缩小后,得到的图形的面积之比是1:9,由此即可解答。
【解答】解:6×3÷9
=18÷9
=2(平方厘米)
答:一个长6厘米,3厘米的长方形按1:3缩小后的面积是2平方厘米。
故答案为:2。
【名师点评】根据图形按照一定的比把图形放大与缩小,则放大与缩小后的面积之比等于这个比的平方。
16.【考点】比例尺应用题.
【答案】15。
【思路分析】先依据“实际距离=图上距离÷比例尺”求出两地的实际距离,再据“路程÷速度=时间”求出货轮从A地到B地需要的时间。
【解答】解:936000000(厘米)
36000000厘米=360(千米)
360÷24=15(小时)
答:到达B港需要15小时。
故答案为:15。
【名师点评】此题主要考查图上距离、实际距离和比例尺的关系以及基本的数量关系“路程÷速度=时间”。
17.【考点】可能性的大小.
【答案】。
【思路分析】20以内质数有:2、3、5、7、11、13、17、19,共8个,然后计算出质数的个数占总数的几分之几。
【解答】解:8÷20
答:从中任意抽取一张,抽到质数的可能性是。
故答案为:。
【名师点评】本题解题关键是能够理解质数的意义,找出20以内质数的个数,再计算出质数的个数占总数的几分之几。
18.【考点】求几个数的最大公因数的方法;求几个数的最小公倍数的方法.
【答案】21。
【思路分析】把A和B公有的质因数连乘起来,所得的积就是它们的最大公因数,把它们公有的质因数和独有的质因数连乘起来,所得的积就是它们的最小公倍数。
【解答】解:因为A=2×n×7,B=5×n×7,所以A和B的最小公倍数是2×5×7×n=70n=210,所以n=210÷70=3;
两数的最大公约数是n×7=3×7=21。
故答案为:21。
【名师点评】熟练掌握用分解质因数的方法求两个数最大公因数和最小公倍数的方法是解题的关键。
19.【考点】分数四则复合应用题.
【答案】见试题解答内容
【思路分析】甲桶油重量的等于乙桶油重量的即甲桶油重量乙桶油重量的,由此得甲桶油重量:乙桶油重量:5,然后找到9千克所对应的份数是5﹣2=3(份),求出1份的数,进而求出乙桶油重.
【解答】解:由题意可得:
甲桶油重量乙桶油重量的
所以甲桶油重量:乙桶油重量:5
乙桶油重:
9÷(5﹣2)×2=9÷3×2=6(千克)
故答案为:6.
【名师点评】此题解答关键是运用“转化”化难为易,把分数转化成两个数量的比,再根据差是9,找出对应的份数即(5﹣2)份,求出一份是多.
20.【考点】百分数的实际应用.
【答案】见试题解答内容
【思路分析】工作总量增加20%,就是原来的1+20%;人数减少了20%,要由原来的80%的人干,每人要干(1+20%)÷80%,然后减去原来的工作效率1就是提高的工作效率.
【解答】解:(1+20%)÷(1﹣20%)﹣1,
=120%÷80%﹣1,
=150%﹣1,
=50%;
答:工作效率要提高50%.
故答案为:50.
【名师点评】总工作量增加,减少这部分人的干的工作量和增加的工作量要平均分到剩下的人来干,由此求出每个人多干的工作量,进而求解.
21.【考点】逆推问题.
【答案】36。
【思路分析】根据题意,我们可先设丙原有糖a颗,则乙给了丙18颗,此时丙有糖(a+18)颗,这正好是甲原有糖的一半,即甲有(2a+36)颗;至此可以看出甲原有的比丙原有的2倍还多36颗,所以甲给乙36颗后正好是丙原有的2倍,这样也就得到了答案。
【解答】解:设丙原有糖a颗,则
(a+18)×2﹣2a
=2a+36﹣2a
=36(颗)
答:甲给了乙36颗糖。
故答案为:36。
【名师点评】解此题只要用字母表示出丙原有糖的颗数,然后用含有同样字母的式子表示出甲原有糖的颗数,通过比较即可轻松作答。
22.【考点】正方形的周长.
【答案】32。
【思路分析】如下图:图中A、B、C、D和整个的大正方形,共5种不同大小的正方形.依题意,A、B、C、D的边长恰好是四个连续整数,因此C的边长比B的边长最多大3厘米;这表明A的边长只能为1厘米,进而得到B、C、D的边长分别为2厘米、4厘米、3厘米;然后根据正方形的周长=边长×4,把数据代入公式解答。
【解答】解:如图:
根据分析可得:
C的边长比B的边长最多大3厘米;
这表明A的边长只能为1厘米,进而得到B、C、D的边长分别为2厘米、4厘米、3厘米;
所以最大正方形的边长是:3+2+3=8(厘米)
则最大正方形的周长是:8×4=32(厘米)
故答案为:32。
【名师点评】此题考查了极值问题,关键是先确定正方形C与B的关系,进而求出ABCD的边长,以及最大正方形的边长。
三.判断题(共6小题)
23.【考点】百分率应用题.
【答案】×
【思路分析】根据百分率的实际意义结合生活实际判断即可。
【解答】解:一种菜籽的出油率应小于100%,所以原题说法错误。
故答案为:×。
【名师点评】本题主要考查百分率的实际应用,关键结合生活实际判断。
24.【考点】负数的意义及其应用.
【答案】√
【思路分析】在数轴上“0”是正、负数的分界点,它既不是正数,也不是负数.
【解答】解:0既不是正数,也不是负数,答案√.
故答案为:√.
【名师点评】根据数轴的认识我们可以知道,0是正、负数的分界点,位于左边的数记作“﹣”,位于右边的数记作“+”,它既不是正数,也不同负数.
25.【考点】百分率应用题.
【答案】×
【思路分析】根据“成活率100%;代入数值,解答即可.
【解答】解:100%=100%;
故答案为:×.
【名师点评】此题属于百分率问题,解答时都是用一部分数量(或全部数量)除以全部数量乘百分之百即可.
26.【考点】图形的拼组.
【答案】×
【思路分析】一副三角板,其中一个三角板的角有30°、60°、90°,等腰直角三角尺的角有45°、45°、90°,用它们进行拼组,即可解答。
【解答】解:分析可知,用一副三角板不可以拼出一个80°的角。所以原题说法错误。
故答案为:×。
【名师点评】本题考查了学生用一副三角尺拼成不同角度的能力,结合题意分析解答即可。
27.【考点】百分数的实际应用.
【答案】×
【思路分析】根据题意,把原价看作单位“1”,提价20%后的价格=原价×(1+20%),又降价20%后的价格等于提价后的价格×(1﹣20%),则现价=原价×(1+20%)×(1﹣20%)=96%原价,据此判断。
【解答】解:现价=原价×(1+20%)×(1﹣20%)
现价=96%×原价
答:原题干说法错误。
故答案为:×。
【名师点评】本题主要考查百分数的应用,关键找到单位“1”,利用关系式做题。
28.【考点】合数分解质因数.
【答案】×
【思路分析】分解质因数就是把一个合数写成几个质数相乘的形式,据此把18分解质因数,一般先从较小的质数试着分解。
【解答】解:把18分解质因数应是:18=2×3×3。所以原题说法错误。
故答案为:×。
【名师点评】此题主要考查分解质因数的方法及其应用,一般先从较小的质数试着分解。
四.计算题(共3小题)
29.【考点】小数除法;分数的加法和减法;小数乘法.
【答案】0.48;57.7;80;。
【思路分析】根据分数、小数加、减、乘、除的计算方法,依次口算结果。
【解答】解:1.2×0.4=0.48
53+4.7=57.7
3.2÷0.04=80
32
【名师点评】本题解题的关键是熟练掌握分数、小数加、减、乘、除的计算方法。
30.【考点】解比例;整数方程求解;小数方程求解.
【答案】x=5,x,x=5。
【思路分析】①根据等式的性质,先在方程两边减7,然后在方程两边除以24,即可解答;
②根据比例的基本性质,内项积等于外项积;然后再根据等式的性质,在方程两边同时除以即可解答;
③根据等式的性质,在方程两边同时减去2.1,然后在方程两边同时除以0.7即可解答。
【解答】解:24x+7=127
24x+7﹣7=127﹣7
24x=120
24x÷24=120÷24
x=5
:x:
x
x
x
x
2.1+0.7x=5.6
2.1+0.7x﹣2.1=5.6﹣2.1
0.7x=3.5
0.7x÷0.7=3.5÷0.7
x=5
【名师点评】此题考查了解方程和解比例的知识,要求学生能够掌握。
31.【考点】小数四则混合运算;分数的四则混合运算;运算定律与简便运算.
【答案】100;1000;5.02;23;;。
【思路分析】先算减法,再算乘法,最后算除法即可;
把32拆封成8×4后,利用乘法结合律即可简便运算;
利用减法的性质即可简便运算;
利用乘法分配律即可简便运算;
逆用乘法分配律即可简便运算;
先算小括号,再算中括号,最后算乘法。
【解答】解:48÷[2.4×(4.4﹣4.2)]
=48÷[2.4×0.2]
=48÷0.48
=100
12.5×32×2.5
=12.5×8×4×2.5
=100×10
=1000
15.02﹣2.4﹣7.6
=15.02﹣(2.4+7.6)
=15.02﹣10
=5.02
121212
=9+10+4
=23
()
1
[]
【名师点评】本题考查了小数和分数的四则混合运算,能用简便方法计算的要用简便方法计算。
五.操作题(共1小题)
32.【考点】作平移后的图形;作旋转一定角度后的图形;图形的放大与缩小.
【答案】(1)(2)(3)
【思路分析】(1)根据平移的方法,画出把梯形向右平移3格后的图形即可。
(2)根据图形放大的方法,把梯形放大到原来的3倍,画出放大后的图形。
(3)根据旋转的方法,点A不动,画出把三角形绕A点按逆时针方向旋转90°后的图形即可。
【解答】解:(1)画出把梯形向右平移3格后的图形。如图:
(2)把梯形放大到原来的3倍,画出放大后的图形。如图:
(3)画出把三角形绕A点按逆时针方向旋转90°后的图形。如图:
【名师点评】本题考查平移、旋转以及图形放大知识,结合题意分析解答即可。
六.应用题(共6小题)
33.【考点】圆锥的体积.
【答案】4.5分米。
【思路分析】根据圆锥的体积公式:Vπr2h,圆柱的体积公式:V=Sh,那么h=V÷S,把数据代入公式解答。
【解答】解:3.14×32×6÷(3.14×22)
3.14×9×6÷(3.14×4)
=56.52÷12.56
=4.5(分米)
答:水深4.5分米。
【名师点评】此题主要考查圆锥、圆柱体积公式的灵活运用,关键是熟记公式。
34.【考点】百分数的实际应用.
【答案】赚了550元。
【思路分析】根据总价=单价×数量,先用35元乘150,求出按定价卖得的钱数;再用(35×80%)乘(250﹣150),求出按定价的八折卖得的钱数;将两部分卖得的钱数相加,再与(30×250)元比较后求差即可。
【解答】解:35×150+(35×80%)×(250﹣150)
=5250+2800
=8050(元)
30×250=7500(元)
8050﹣7500=550(元)
答:商店赚了550元。
【名师点评】解答本题需明确进价、定价和折扣价的意义,熟练掌握单价、数量和总价之间的关系。
35.【考点】百分数的实际应用.
【答案】90千米。
【思路分析】先利用“路程=速度×时间”求出两车行驶的总路程;再利用“已知一个数的百分之几是多少,求这个数,用除法计算”的方法即可求出全程。根据时间=路程÷速度,计算出甲车到B地的时间,根据路程=速度×时间,计算出乙车已行的路程,最后用全程减去乙车已行的路程,计算出乙车离A地还有多少千米。
【解答】解:(50+40)×4÷80%
=90×4÷0.8
=360÷0.8
=450(千米)
450÷50=9(小时)
450﹣40×9
=450﹣360
=90(千米)
答:乙车离A地还有90千米。
【名师点评】此题主要考查路程、速度和时间之间的关系及已知一个数的百分之几是多少,求这个数,用除法计算。再根据路程、速度、时间的关系,列式计算。
36.【考点】圆柱的侧面积、表面积和体积.
【答案】B,15.7平方分米。
【思路分析】根据圆柱侧面展开图的特征,圆柱的侧面沿高展开是一个长方形,这个长方形的长等于圆柱底面周长,长方形的宽等于圆柱的高。由此可知焊成的两个圆柱的侧面积相等,所以比较两个圆柱的底面积即可。
【解答】解:A的底面积:
3.14×(12.56÷3.14÷2)2
=3.14×4
=12.56(平方分米)
B的底面积:
3.14×(18.84÷3.14÷2)2
=3.14×9
=28.26(平方分米)
28.26﹣12.56=15.7(平方分米)
答:B圆柱的表面积大些,大15.7平方分米。
【名师点评】此题主要考查圆柱表面积公式的灵活运用,关键是熟记公式。
37.【考点】简单的归总应用题.
【答案】96天。
【思路分析】用原来平均每天照明用电量乘用电天数求出30天的用电量,再用求得的用电量除以现在每天的用电量即可求出用电天数。
【解答】解:80×30÷25
=2400÷25
=96(天)
答:原来30天的用电量现在可以用96天。
【名师点评】解答此题根据乘除法的意义进行列式计算。
38.【考点】百分数的实际应用.
【答案】538千米。
【思路分析】根据2015年重庆轨道交通里程约占北京的,而2015年北京轨道交通里程大约528km,根据求一个数的几分之几是多少,用乘法计算,用2015年北京轨道交通里程数乘2015年重庆轨道交通里程约占北京的分率即可求出2015年重庆市的轨道交通里程数;而2024年初重庆轨道交通里程是2015年的2.69倍,根据乘法的意义,用2015年重庆轨道交通里程数乘2.69即可求解2024年初重庆轨道交通里程数,据此解答。
【解答】解:5282.69
=200×2.69
=538(km)
答:2024年初,重庆轨道交通里程是538千米。
【名师点评】本题考查了分数乘法计算的应用。
21世纪教育网(www.21cnjy.com)
2025年秋六年级数学小升初开学重点校分班摸底预测卷(西师大版)
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题(共10小题)
1.一辆自行车,行驶中后齿轮转24圈,前齿轮转14圈,则前齿轮和后齿轮的齿数最简比( )
A.12:7 B.14:24 C.7:12 D.24:14
2.一种运动鞋,在“6.18网购节”时,先提价20%后又打八折,与原价相比,现价( )
A.降低了 B.提高了 C.不变 D.无法确定
3.如图所示,把底面直径是8cm的圆柱切成若干等份,拼成一个近似的长方体,这个长方体的表面积比原来增加了80cm2,那么长方体的体积是( )cm3。
A.251.2 B.502.4 C.2009.6 D.1004.8
4.下列说法错误的有( )项。
①把一个圆柱的侧面剪开,不可能得到平行四边形。
②平行四边形的面积一定,它的底和对应的高成反比例。
③实际距离一定比相对应的图上距离大。
④一个长方形面积一定时,它的长与宽的关系用图像表示出来是一条直线。
A.1 B.2 C.3 D.4
5.现在从甲、乙、丙、丁四个人中选出两个人参加一项活动。规定:如果甲去,那么乙也去;如果丙不去,那么乙也不去;如果丙去;那么丁不去。最后去参加活动的两个人是( )
A.甲、乙 B.甲、丙 C.乙、丙 D.乙、丁
6.甲从A地出发向B地,同时,乙、丙两人从B地驾车出发,向A地行驶,甲、乙两人相遇在离A地3千米的C地,乙到A地后立即掉头,与丙在C地相遇,若开始出发时甲就跑步,速度提高到步行速度的2.5倍,则甲、丙相遇地点距A地7.5 千米,A、B两地距离( )千米。
A.21 B.22.5 C.24 D.25.5
7.如图,一只小甲虫从A点出发沿着线段或弧线走到了B点,要求途中不能重复经过任何点,那么这只甲虫可走的不同路线一共有( )种。
A.64 B.72 C.128 D.144
8.把下面的立体图形切一刀,截面形状不可能是长方形的是( )
A. B. C. D.
9.一个盒子里装有同样大小的红球、黄球、白球各6个,要想摸出的球一定有两个同色的,至少要摸出( )个球。
A.7 B.6 C.5 D.4
10.一项工程,甲单独做需要10小时完成,乙单独做需要15小时完成。现在两人合作,中途甲因事停工了一段时间,结果7小时才完成,甲停工了( )小时。
A.3.5 B.3 C. D.18
二.填空题(共12小题)
11.如图是某种汽车所行路程与耗油量的对应数值表。该种汽车所行路程与耗油量关系成比例,说说你的理由: 。
行驶路程/km 15 30 45 75
耗油量/L 2 4 6 10
12.一个圆柱的侧面积是188.4dm2,高是10dm,这个圆柱的体积是 dm3;如果把它削成一个最大的圆锥体,则削去部分的体积是 dm3。
13.今年父亲比儿子大27岁,3年后父亲的年龄是儿子的4倍,那么儿子今年 岁。
14.在周长为40米的圆形水池边每隔2米摆一盆花,需放 盆花。
15.把一个长6厘米,宽3厘米的长方形按1:3缩小后的面积是 平方厘米。
16.在比例尺是1:4000000的地图上,量得A、B两港距离为9厘米,一艘货轮以每小时24千米的速度从A开向B港,到达B港需要 小时。
17.在20张同样的卡片上分别写上1~20各数,将卡片打乱,从中任意抽取一张,抽到质数的可能性是 。
18.把两个自然数A和B分解质因数:A=2×n×7,B=5×n×7,已知A和B的最小公倍数是210,则两数的最大公约数是 。
19.甲乙两桶油重量差为9千克,甲桶油重量的等于乙桶油重量的,则乙桶油重 千克.
20.一个工厂改革后人员减少20%,产量比原来增加20%,每人工作效率提高 %.
21.甲、乙、丙三人各有一些糖;如果甲的糖数变为原来一半。乙给丙18颗,那么三人的糖数一样多;如果丙的糖数变为原来的2倍,甲给乙一些糖,三人的糖数也能一样多,那么甲给了乙 颗糖。
22.在如图所示的图案中,共可以找到5种不同大小的正方形。若其中较小的四种正方形的边长恰好是四个连续整数(单位:厘米),则其中最大的正方形的周长为 厘米。
三.判断题(共6小题)
23.一种菜籽的出油率达到了120%。
24.0既不是正数也不是负数. .
25.小华家栽了99棵树,活了99棵,成活率是99%.
26.用一副三角板可以拼出一个80°的角。
27.一台电视机提价20%后,又降价20%,价格不变。
28.把18写成质数相乘的形式:18=1×2×3×3。
四.计算题(共3小题)
29.直接写出得数。
1.2×0.4= 53+4.7= 3.2÷0.04= 3
30.解方程。
24x+7=127 2.1+0.7x=5.6
31.计算下面各题,能简算的要简算。
48÷[2.4×(4.4﹣4.2)] 12.5×32×2.5
15.02﹣2.4﹣7.6
五.操作题(共1小题)
32.按要求画一画。
(1)画出把梯形向右平移3格后的图形。
(2)把梯形放大到原来的3倍,画出放大后的图形。
(3)画出把三角形绕A点按逆时针方向旋转90°后的图形。
六.应用题(共6小题)
33.一个底面半径3dm,高6dm的圆锥容器里装满了水,将其全部倒入底面半径2dm,高5dm的圆柱形容器里。水深有多少分米?
34.书店以每本30元的价格买进了250本图书。销售时,先以每本35元的定价卖了150本,其余的按定价的八折全部卖完。这个商店赚了(或亏了)多少元?
35.甲、乙两辆汽车分别同时从A、B两地相对开出,甲车每小时行驶50千米,乙车每小时行驶40千米,经过4小时两车共行了全程的80%。当甲车到达B地时,乙车离A地还有多少千米?
36.有两张长18.84dm,宽12.56dm的铁皮,一张顺着长(长为高)卷成一个最大的圆柱A,一张顺着宽(宽为高)卷成一个最大的圆柱B,分别给两个圆柱焊上一个底面。哪个圆柱的表面积大些?大多少平方分米?
37.高新区综合办公大楼原来平均每天照明用电80千瓦时。改用节能灯以后,平均每天只用电25千瓦时。原来30天的用电量现在可以用多少天?
38.北京轨道交通里程大约528km,重庆轨道交通里程约占北京的。近十年重庆轨道交通快速发展,到2024年初重庆轨道交通里程是2015年的2.69倍,约占同时期北京轨道交通里程的64.3%。2024年初,重庆轨道交通里程是多少千米?
参考答案及试题解析
一.选择题(共10小题)
1.【考点】比的意义.
【答案】A
【思路分析】根据题意可知:前、后齿轮走过的路程是相同的,也就是齿轮的齿数×转动的圈数=走过的路程(一定),所以齿数与转的圈数乘反比例,据此解答即可。
【解答】解:设前齿轮和后齿轮的齿数分别是x、y。
14x=24y
x:y=24:14=12:7
答:前齿轮和后齿轮的齿数最简比是12:7。
故选:A。
【名师点评】知道齿轮的齿数×转动的圈数=走过的路程(一定),是解答此题的关键。
2.【考点】百分数的实际应用.
【答案】A
【思路分析】把原价看作单位“1”,提价20%后,价格为原价的(1+20%),又打八折价格为原价的(1+20%)×80%,据此解答。
【解答】解:1×(1+20%)×80%
=120%×80%
=96%
即现在的价格是原价的96%,所以现在的价格降了。
答:现在的价格降了。
故选:A。
【名师点评】本题主要考查百分数的实际应用,把原价看作单位“1”,是解答关键。
3.【考点】圆柱的侧面积、表面积和体积.
【答案】B
【思路分析】根据圆柱体积公式的推导过程可知,把一个圆柱切拼成一个近似长方体,体积不变。拼成的长方体的表面积比圆柱的表面积增加了两个切面的面积,每个切面的长等于圆柱的高,每个切面的宽等于圆柱的底面半径,根据长方形的面积公式:S=ab,把数据代入公式求出圆柱的高,然后根据圆柱的体积公式:V=πr2h,把数据代入公式解答。
【解答】解:80÷2÷(8÷2)
=40÷4
=10(厘米)
3.14×(8÷2)2×10
=3.14×16×10
=50.24×10
=502.4(立方厘米)
答:长方体的体积是502.4立方厘米。
故选:B。
【名师点评】此题考查的目的是理解掌握圆柱体积公式的推导过程及应用,长方形的面积公式及应用,关键是熟记公式。
4.【考点】辨识成正比例的量与成反比例的量;圆柱的展开图.
【答案】C
【思路分析】根据辨识成正比例的量与成反比例的量的方法以及比例尺的意义、圆柱的展开图知识,分析解答即可。
【解答】解:①把一个圆柱的侧面剪开,可能得到长方形、正方形或平行四边形,所以本选项说法错误;
②平行四边形的面积一定,是乘积一定,所以底和对应的高成反比例,所以本选项说法正确;
③当实际距离比较大时,所画的图上距离要比实际距离小,当实际长度较小时,如手表等精密零件,所画的图上距离要比实际距离大,因此,实际距离一定比相对应的图上距离要大这种说法是错误的;
④一个长方形面积一定时,是乘积一定,它的长与宽的关系是反比例关系,用图像表示出来不是一条直线。所以本选项说法错误。
故选:C。
【名师点评】本题考查了辨识成正比例的量与成反比例的量的方法以及比例尺的意义、圆柱的展开图知识,结合题意分析解答即可。
5.【考点】逻辑推理;盈亏问题.
【答案】C
【思路分析】①根据如果甲去,那么乙也去,可得甲去,乙必然也去;②又根据如果丙不去,那么乙也不去,可得如果乙去了,丙也一定去了,同时满足①②的条件和“如果丙去;那么丁不去”只能是乙、丙参加了活动,据此解答即可。
【解答】解:根据如果甲去,那么乙也去,可得甲去,乙必然也去,又根据如果丙不去,那么乙也不去,可得如果乙去了,丙也一定去了,如果丙去;那么丁不去,可得:如果丙不去;那么丁去,同时乙也不去,则根据“甲去,那么乙也去”可得甲也不去,这样只有丁去,这与两个人参加一项活动相矛盾。同时满足条件只能是乙、丙参加了活动。
故选:C。
【名师点评】本题的关键是根据如果甲去,那么乙也去;如果丙不去,那么乙也不去的话入手,来进行推理。
6.【考点】相遇问题.
【答案】A
【思路分析】若开始出发时甲就跑步,速度提高到步行速度的2.5倍,则甲原来走3千米,甲提高速度后走的路程就是3×2.5=7.5千米,而这时甲、丙相遇地点距A地7.5千米。可知两次相遇用的时间相同。因两次相遇时的时间相同,所以乙丙二人的速度比是(3+3):(7.5﹣3)=4:3,把第一次相遇时,丙走的路程看作单位“1”,依据时间一定,速度和路程成正比,可得甲走了丙的路程,此时乙比丙多走7.5﹣3=4.5千米,依据分数除法意义,求出丙走的路程,再加上7.5就是A、B两地间的路程。
【解答】解:乙、丙的速度比是:(3+3):(7.5﹣3)=4:3。
(7.5﹣3)÷(1)+7.5
=4.57.5
=13.5+7.5
=21(千米)
答:A、B两地距离21千米。
故选:A。
【名师点评】解答此题的关键是明确提速前甲乙相遇时间和提速后甲丙时间相同。
7.【考点】简单的排列、组合.
【答案】C
【思路分析】
小甲虫想要到B点必须通过交点上C、D、E、F四个点才能到达B;
小虫甲从A到C有4种,从C到D有4种;从D到B有4种;共有4×4×4=64(种);
同理小虫从A通过其他E、F个点到B点也是64种,
所以共有4×4×4×2种。
【解答】解:4×4×4×2
=64×2
=128(种)
答:这只甲虫可走的不同路线一共有128种。
故选:C。
【名师点评】本题考查了乘法原理和加法原理的综合应用,关键是确定每一步有几种走法。
8.【考点】圆柱的特征;长方体的特征;正方体的特征.
【答案】D
【思路分析】用一个平面截一个几何体得到的形状叫做几何体的截面,据此分析解答。
【解答】解:圆柱,正方体,长方体的截面都可能出现长方形,只有球的截面只与圆有关。
故选:D。
【名师点评】本题考查了立体图形截面形状的认识。
9.【考点】抽屉原理.
【答案】D
【思路分析】最坏情况是红球、白球、黄球各摸出1个,此时再摸出1个球,一定有2个同色的,一共需要摸出4个球。
【解答】解:考虑最差情况:摸出2个球,分别是红球、黄球、白球各1个,
那么再任意摸出1个球,一定可以保证有2个球颜色相同,
3+1=4(个)
答:要想摸出的球一定有两个是同色的,至少要摸出4个球。
故选:D。
【名师点评】此题考查了利用抽屉原理解决实际问题的灵活应用,关键是从最差情况考虑。
10.【考点】工程问题.
【答案】C
【思路分析】将工作总量看作单位“1“,设甲停工了 x 小时,根据甲的效率×工作时间+乙的效率×工作时间=1,列出方程,求出x的值即可。
【解答】解:甲的效率:
乙的效率:
设甲停工了 x 小时。
(7﹣x )7=1
x1
1x
x
x=1
答:甲停工了1时。
故选:C。
【名师点评】关键是找到等量关系,理解工作效率、工作时间、工作总量之间的关系,其中时间分之一可以看作效率。
二.填空题(共12小题)
11.【考点】辨识成正比例的量与成反比例的量.
【答案】因为15÷2=30÷4=45÷6=75÷10=7.5,符合正比例关系式x:y=k(一定),所以汽车行驶路程与耗油量是正比例关系。
【思路分析】表中有两种相关联的量,行驶的路程和耗油量,耗油量随着行驶的路程变化而变化,且耗油量与行驶路程的比值是一定的,因为15÷2=30÷4=45÷6=75÷10=7.5,符合正比例关系式x:y=k(一定),所以汽车行驶路程与耗油量是正比例关系,据此解答即可。
【解答】解:该种汽车所行路程与耗油量关系成正比例,因为15÷2=30÷4=45÷6=75÷10=7.5,符合正比例关系式x:y=k(一定),所以汽车行驶路程与耗油量是正比例关系。
故答案为:因为15÷2=30÷4=45÷6=75÷10=7.5,符合正比例关系式x:y=k(一定),所以汽车行驶路程与耗油量是正比例关系。
【名师点评】此题主要考查正比例的意义的实际应用,结合题意分析解答即可。
12.【考点】圆柱的侧面积、表面积和体积;圆锥的体积.
【答案】282.6,188.4。
【思路分析】根据圆柱的侧面积公式:S=2πrh,据此可以求出圆柱的底面半径,再根据圆柱的体积公式:V=πr2h,把数据代入公式求出圆柱的体积,如果把它削成一个最大的圆锥体,则削去部分的体积是圆柱体积的(1),据此解答即可。
【解答】解:188.4÷10÷3.14÷2
=18.84÷3.14÷2
=6÷2
=3(分米)
3.14×32×10
=3.14×9×10
=28.26×10
=282.6(立方分米)
282.6÷3×2
=94.2×2
=188.4(立方分米)
答:这个圆柱的体积是282.6立方分米,如果把它削成一个最大的圆锥体,则削去部分的体积是188.4立方分米。
故答案为:282.6,188.4。
【名师点评】此题主要考查圆柱的侧面积公式、圆柱的体积公式的灵活应用,以及等底等高的圆柱与圆锥体积之间的关系及应用。
13.【考点】年龄问题.
【答案】见试题解答内容
【思路分析】根据年龄差不会随时间的变化而改变,知道3年后父子的年龄差是27岁,由此根据差倍关系求出3年后儿子的年龄,进而求出儿子今年的年龄.
【解答】解:4﹣1=3;
27÷3=9(岁);
9﹣3=6(岁);
答:儿子今年6岁.
故答案为:6.
【名师点评】关键是根据年龄差不会随时间的变化而改变,利用差倍公式{差÷(倍数﹣1)=小数,小数×倍数=大数,(或 小数+差=大数)解决问题.
14.【考点】植树问题.
【答案】20。
【思路分析】围成圆圈摆放花盆,花盆数=间隔数,由此求出40米里有几个2米的间隔,就有几盆花。
【解答】解:40÷2=20(盆)
答:需放20盆花。
故答案为:20。
【名师点评】此题属于围成圆圈植树问题,植树棵数=间隔数。
15.【考点】图形的放大与缩小.
【答案】2。
【思路分析】长方形按1:3缩小后,得到的图形的面积之比是1:9,由此即可解答。
【解答】解:6×3÷9
=18÷9
=2(平方厘米)
答:一个长6厘米,3厘米的长方形按1:3缩小后的面积是2平方厘米。
故答案为:2。
【名师点评】根据图形按照一定的比把图形放大与缩小,则放大与缩小后的面积之比等于这个比的平方。
16.【考点】比例尺应用题.
【答案】15。
【思路分析】先依据“实际距离=图上距离÷比例尺”求出两地的实际距离,再据“路程÷速度=时间”求出货轮从A地到B地需要的时间。
【解答】解:936000000(厘米)
36000000厘米=360(千米)
360÷24=15(小时)
答:到达B港需要15小时。
故答案为:15。
【名师点评】此题主要考查图上距离、实际距离和比例尺的关系以及基本的数量关系“路程÷速度=时间”。
17.【考点】可能性的大小.
【答案】。
【思路分析】20以内质数有:2、3、5、7、11、13、17、19,共8个,然后计算出质数的个数占总数的几分之几。
【解答】解:8÷20
答:从中任意抽取一张,抽到质数的可能性是。
故答案为:。
【名师点评】本题解题关键是能够理解质数的意义,找出20以内质数的个数,再计算出质数的个数占总数的几分之几。
18.【考点】求几个数的最大公因数的方法;求几个数的最小公倍数的方法.
【答案】21。
【思路分析】把A和B公有的质因数连乘起来,所得的积就是它们的最大公因数,把它们公有的质因数和独有的质因数连乘起来,所得的积就是它们的最小公倍数。
【解答】解:因为A=2×n×7,B=5×n×7,所以A和B的最小公倍数是2×5×7×n=70n=210,所以n=210÷70=3;
两数的最大公约数是n×7=3×7=21。
故答案为:21。
【名师点评】熟练掌握用分解质因数的方法求两个数最大公因数和最小公倍数的方法是解题的关键。
19.【考点】分数四则复合应用题.
【答案】见试题解答内容
【思路分析】甲桶油重量的等于乙桶油重量的即甲桶油重量乙桶油重量的,由此得甲桶油重量:乙桶油重量:5,然后找到9千克所对应的份数是5﹣2=3(份),求出1份的数,进而求出乙桶油重.
【解答】解:由题意可得:
甲桶油重量乙桶油重量的
所以甲桶油重量:乙桶油重量:5
乙桶油重:
9÷(5﹣2)×2=9÷3×2=6(千克)
故答案为:6.
【名师点评】此题解答关键是运用“转化”化难为易,把分数转化成两个数量的比,再根据差是9,找出对应的份数即(5﹣2)份,求出一份是多.
20.【考点】百分数的实际应用.
【答案】见试题解答内容
【思路分析】工作总量增加20%,就是原来的1+20%;人数减少了20%,要由原来的80%的人干,每人要干(1+20%)÷80%,然后减去原来的工作效率1就是提高的工作效率.
【解答】解:(1+20%)÷(1﹣20%)﹣1,
=120%÷80%﹣1,
=150%﹣1,
=50%;
答:工作效率要提高50%.
故答案为:50.
【名师点评】总工作量增加,减少这部分人的干的工作量和增加的工作量要平均分到剩下的人来干,由此求出每个人多干的工作量,进而求解.
21.【考点】逆推问题.
【答案】36。
【思路分析】根据题意,我们可先设丙原有糖a颗,则乙给了丙18颗,此时丙有糖(a+18)颗,这正好是甲原有糖的一半,即甲有(2a+36)颗;至此可以看出甲原有的比丙原有的2倍还多36颗,所以甲给乙36颗后正好是丙原有的2倍,这样也就得到了答案。
【解答】解:设丙原有糖a颗,则
(a+18)×2﹣2a
=2a+36﹣2a
=36(颗)
答:甲给了乙36颗糖。
故答案为:36。
【名师点评】解此题只要用字母表示出丙原有糖的颗数,然后用含有同样字母的式子表示出甲原有糖的颗数,通过比较即可轻松作答。
22.【考点】正方形的周长.
【答案】32。
【思路分析】如下图:图中A、B、C、D和整个的大正方形,共5种不同大小的正方形.依题意,A、B、C、D的边长恰好是四个连续整数,因此C的边长比B的边长最多大3厘米;这表明A的边长只能为1厘米,进而得到B、C、D的边长分别为2厘米、4厘米、3厘米;然后根据正方形的周长=边长×4,把数据代入公式解答。
【解答】解:如图:
根据分析可得:
C的边长比B的边长最多大3厘米;
这表明A的边长只能为1厘米,进而得到B、C、D的边长分别为2厘米、4厘米、3厘米;
所以最大正方形的边长是:3+2+3=8(厘米)
则最大正方形的周长是:8×4=32(厘米)
故答案为:32。
【名师点评】此题考查了极值问题,关键是先确定正方形C与B的关系,进而求出ABCD的边长,以及最大正方形的边长。
三.判断题(共6小题)
23.【考点】百分率应用题.
【答案】×
【思路分析】根据百分率的实际意义结合生活实际判断即可。
【解答】解:一种菜籽的出油率应小于100%,所以原题说法错误。
故答案为:×。
【名师点评】本题主要考查百分率的实际应用,关键结合生活实际判断。
24.【考点】负数的意义及其应用.
【答案】√
【思路分析】在数轴上“0”是正、负数的分界点,它既不是正数,也不是负数.
【解答】解:0既不是正数,也不是负数,答案√.
故答案为:√.
【名师点评】根据数轴的认识我们可以知道,0是正、负数的分界点,位于左边的数记作“﹣”,位于右边的数记作“+”,它既不是正数,也不同负数.
25.【考点】百分率应用题.
【答案】×
【思路分析】根据“成活率100%;代入数值,解答即可.
【解答】解:100%=100%;
故答案为:×.
【名师点评】此题属于百分率问题,解答时都是用一部分数量(或全部数量)除以全部数量乘百分之百即可.
26.【考点】图形的拼组.
【答案】×
【思路分析】一副三角板,其中一个三角板的角有30°、60°、90°,等腰直角三角尺的角有45°、45°、90°,用它们进行拼组,即可解答。
【解答】解:分析可知,用一副三角板不可以拼出一个80°的角。所以原题说法错误。
故答案为:×。
【名师点评】本题考查了学生用一副三角尺拼成不同角度的能力,结合题意分析解答即可。
27.【考点】百分数的实际应用.
【答案】×
【思路分析】根据题意,把原价看作单位“1”,提价20%后的价格=原价×(1+20%),又降价20%后的价格等于提价后的价格×(1﹣20%),则现价=原价×(1+20%)×(1﹣20%)=96%原价,据此判断。
【解答】解:现价=原价×(1+20%)×(1﹣20%)
现价=96%×原价
答:原题干说法错误。
故答案为:×。
【名师点评】本题主要考查百分数的应用,关键找到单位“1”,利用关系式做题。
28.【考点】合数分解质因数.
【答案】×
【思路分析】分解质因数就是把一个合数写成几个质数相乘的形式,据此把18分解质因数,一般先从较小的质数试着分解。
【解答】解:把18分解质因数应是:18=2×3×3。所以原题说法错误。
故答案为:×。
【名师点评】此题主要考查分解质因数的方法及其应用,一般先从较小的质数试着分解。
四.计算题(共3小题)
29.【考点】小数除法;分数的加法和减法;小数乘法.
【答案】0.48;57.7;80;。
【思路分析】根据分数、小数加、减、乘、除的计算方法,依次口算结果。
【解答】解:1.2×0.4=0.48
53+4.7=57.7
3.2÷0.04=80
32
【名师点评】本题解题的关键是熟练掌握分数、小数加、减、乘、除的计算方法。
30.【考点】解比例;整数方程求解;小数方程求解.
【答案】x=5,x,x=5。
【思路分析】①根据等式的性质,先在方程两边减7,然后在方程两边除以24,即可解答;
②根据比例的基本性质,内项积等于外项积;然后再根据等式的性质,在方程两边同时除以即可解答;
③根据等式的性质,在方程两边同时减去2.1,然后在方程两边同时除以0.7即可解答。
【解答】解:24x+7=127
24x+7﹣7=127﹣7
24x=120
24x÷24=120÷24
x=5
:x:
x
x
x
x
2.1+0.7x=5.6
2.1+0.7x﹣2.1=5.6﹣2.1
0.7x=3.5
0.7x÷0.7=3.5÷0.7
x=5
【名师点评】此题考查了解方程和解比例的知识,要求学生能够掌握。
31.【考点】小数四则混合运算;分数的四则混合运算;运算定律与简便运算.
【答案】100;1000;5.02;23;;。
【思路分析】先算减法,再算乘法,最后算除法即可;
把32拆封成8×4后,利用乘法结合律即可简便运算;
利用减法的性质即可简便运算;
利用乘法分配律即可简便运算;
逆用乘法分配律即可简便运算;
先算小括号,再算中括号,最后算乘法。
【解答】解:48÷[2.4×(4.4﹣4.2)]
=48÷[2.4×0.2]
=48÷0.48
=100
12.5×32×2.5
=12.5×8×4×2.5
=100×10
=1000
15.02﹣2.4﹣7.6
=15.02﹣(2.4+7.6)
=15.02﹣10
=5.02
121212
=9+10+4
=23
()
1
[]
【名师点评】本题考查了小数和分数的四则混合运算,能用简便方法计算的要用简便方法计算。
五.操作题(共1小题)
32.【考点】作平移后的图形;作旋转一定角度后的图形;图形的放大与缩小.
【答案】(1)(2)(3)
【思路分析】(1)根据平移的方法,画出把梯形向右平移3格后的图形即可。
(2)根据图形放大的方法,把梯形放大到原来的3倍,画出放大后的图形。
(3)根据旋转的方法,点A不动,画出把三角形绕A点按逆时针方向旋转90°后的图形即可。
【解答】解:(1)画出把梯形向右平移3格后的图形。如图:
(2)把梯形放大到原来的3倍,画出放大后的图形。如图:
(3)画出把三角形绕A点按逆时针方向旋转90°后的图形。如图:
【名师点评】本题考查平移、旋转以及图形放大知识,结合题意分析解答即可。
六.应用题(共6小题)
33.【考点】圆锥的体积.
【答案】4.5分米。
【思路分析】根据圆锥的体积公式:Vπr2h,圆柱的体积公式:V=Sh,那么h=V÷S,把数据代入公式解答。
【解答】解:3.14×32×6÷(3.14×22)
3.14×9×6÷(3.14×4)
=56.52÷12.56
=4.5(分米)
答:水深4.5分米。
【名师点评】此题主要考查圆锥、圆柱体积公式的灵活运用,关键是熟记公式。
34.【考点】百分数的实际应用.
【答案】赚了550元。
【思路分析】根据总价=单价×数量,先用35元乘150,求出按定价卖得的钱数;再用(35×80%)乘(250﹣150),求出按定价的八折卖得的钱数;将两部分卖得的钱数相加,再与(30×250)元比较后求差即可。
【解答】解:35×150+(35×80%)×(250﹣150)
=5250+2800
=8050(元)
30×250=7500(元)
8050﹣7500=550(元)
答:商店赚了550元。
【名师点评】解答本题需明确进价、定价和折扣价的意义,熟练掌握单价、数量和总价之间的关系。
35.【考点】百分数的实际应用.
【答案】90千米。
【思路分析】先利用“路程=速度×时间”求出两车行驶的总路程;再利用“已知一个数的百分之几是多少,求这个数,用除法计算”的方法即可求出全程。根据时间=路程÷速度,计算出甲车到B地的时间,根据路程=速度×时间,计算出乙车已行的路程,最后用全程减去乙车已行的路程,计算出乙车离A地还有多少千米。
【解答】解:(50+40)×4÷80%
=90×4÷0.8
=360÷0.8
=450(千米)
450÷50=9(小时)
450﹣40×9
=450﹣360
=90(千米)
答:乙车离A地还有90千米。
【名师点评】此题主要考查路程、速度和时间之间的关系及已知一个数的百分之几是多少,求这个数,用除法计算。再根据路程、速度、时间的关系,列式计算。
36.【考点】圆柱的侧面积、表面积和体积.
【答案】B,15.7平方分米。
【思路分析】根据圆柱侧面展开图的特征,圆柱的侧面沿高展开是一个长方形,这个长方形的长等于圆柱底面周长,长方形的宽等于圆柱的高。由此可知焊成的两个圆柱的侧面积相等,所以比较两个圆柱的底面积即可。
【解答】解:A的底面积:
3.14×(12.56÷3.14÷2)2
=3.14×4
=12.56(平方分米)
B的底面积:
3.14×(18.84÷3.14÷2)2
=3.14×9
=28.26(平方分米)
28.26﹣12.56=15.7(平方分米)
答:B圆柱的表面积大些,大15.7平方分米。
【名师点评】此题主要考查圆柱表面积公式的灵活运用,关键是熟记公式。
37.【考点】简单的归总应用题.
【答案】96天。
【思路分析】用原来平均每天照明用电量乘用电天数求出30天的用电量,再用求得的用电量除以现在每天的用电量即可求出用电天数。
【解答】解:80×30÷25
=2400÷25
=96(天)
答:原来30天的用电量现在可以用96天。
【名师点评】解答此题根据乘除法的意义进行列式计算。
38.【考点】百分数的实际应用.
【答案】538千米。
【思路分析】根据2015年重庆轨道交通里程约占北京的,而2015年北京轨道交通里程大约528km,根据求一个数的几分之几是多少,用乘法计算,用2015年北京轨道交通里程数乘2015年重庆轨道交通里程约占北京的分率即可求出2015年重庆市的轨道交通里程数;而2024年初重庆轨道交通里程是2015年的2.69倍,根据乘法的意义,用2015年重庆轨道交通里程数乘2.69即可求解2024年初重庆轨道交通里程数,据此解答。
【解答】解:5282.69
=200×2.69
=538(km)
答:2024年初,重庆轨道交通里程是538千米。
【名师点评】本题考查了分数乘法计算的应用。
21世纪教育网(www.21cnjy.com)
同课章节目录
