(小升初开学分班考)小升初开学重点校分班摸底培优卷-2025年秋六年级数学青岛版(六三学制)(含答案解析)
文档属性
| 名称 | (小升初开学分班考)小升初开学重点校分班摸底培优卷-2025年秋六年级数学青岛版(六三学制)(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 205.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-16 12:47:15 | ||
图片预览



文档简介
/ 让学习更有效 小升初备考 | 数学学科
2025年秋六年级数学小升初开学重点校分班摸底培优卷青岛版(六三制)
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题
1.下面选项中两种量成正比例的是( )
A.正方形的边长与面积。
B.圆柱的体积一定,它的底面积与高。
C.比例尺一定,图上距离与实际距离。
2.李爷爷查看15日天气预报,其中8天是晴天,4天是阴天,3天是雨天。从中任选一天,选中( )天的可能性最大。
A.晴 B.阴 C.雨
3.小红所在的小组共4人,体重最重的是42千克,小红最轻是38.2千克,已知她们的平均体重是40.8千克,其他两人的体重可能是( )
A.39 40 B.40 41 C.41 42
4.在推导多边形面积时,如图的方法中只用到平移的是( )
A.
B.
C.
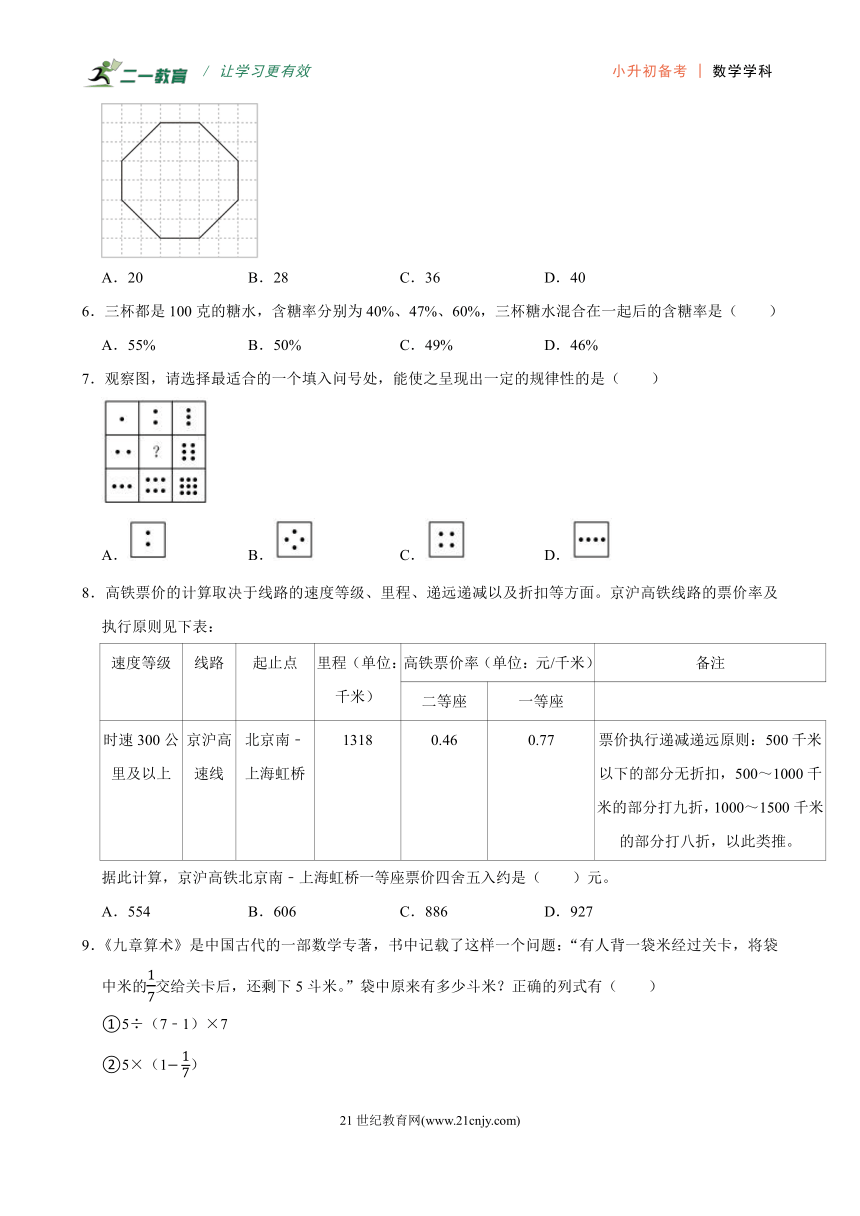
5.一只蜘蛛在纱门上织了一张网(如图),若图中每个小正方形的面积为1平方单位,则蜘蛛网覆盖的面积是( )平方单位。
A.20 B.28 C.36 D.40
6.三杯都是100克的糖水,含糖率分别为40%、47%、60%,三杯糖水混合在一起后的含糖率是( )
A.55% B.50% C.49% D.46%
7.观察图,请选择最适合的一个填入问号处,能使之呈现出一定的规律性的是( )
A. B. C. D.
8.高铁票价的计算取决于线路的速度等级、里程、递远递减以及折扣等方面。京沪高铁线路的票价率及执行原则见下表:
速度等级 线路 起止点 里程(单位:千米) 高铁票价率(单位:元/千米) 备注
二等座 一等座
时速300公里及以上 京沪高速线 北京南﹣上海虹桥 1318 0.46 0.77 票价执行递减递远原则:500千米以下的部分无折扣,500~1000千米的部分打九折,1000~1500千米的部分打八折,以此类推。
据此计算,京沪高铁北京南﹣上海虹桥一等座票价四舍五入约是( )元。
A.554 B.606 C.886 D.927
9.《九章算术》是中国古代的一部数学专著,书中记载了这样一个问题:“有人背一袋米经过关卡,将袋中米的交给关卡后,还剩下5斗米。”袋中原来有多少斗米?正确的列式有( )
①5÷(7﹣1)×7
②5×(1)
③5÷(1)
A.①③ B.②③ C.①②
10.印刷用纸通常用A2、A3、A4、A5等编号表示大小规格,A4纸是A3纸的一半,A5纸是A4纸的一半,按照这样编号规则,A5纸的面积是A2纸的( )
A.20% B.25% C.6.25% D.12.5%
二.填空题
11.如图,阴影部分可以用分数表示为 。
12.丽丽用橡皮泥做了一个高为6厘米的圆柱,如果把这个圆柱平均截成3段(如图),表面积比原来增加50.24平方厘米,原来圆柱的底面面积是 平方厘米,如果把截成的其中一段捏成一个底面与它相等的圆锥,圆锥的高是 厘米,圆锥的体积比原来未截之前的圆柱体积少_______ 立方厘米。
13.中国农历中的夏至是一年中白昼最长、黑夜最短的一天。2023年6月21日这一天是夏至,德州的黑夜时间约是白昼时间的,夏至这一天德州的白昼时间有 小时。
14.A4纸的秘密:一张A4纸,规格是210×297(单位:mm),经过以下两次对折,可以得到如图图形,则最后图中小阴影三角形的周长是 mm。
15.规定运算a△b的结果按照下述方式产生:在a的倍数中找出大于b且最小的一个,计算这个倍数与b的差,如7Δ15=7×3﹣15=6,9Δ6=9×1﹣6=3。那么25△2023= 。
16.实验小学象棋活动室有象棋和跳棋共7副,如果2人下一副象棋,6人下一副跳棋,恰好可供26名学生同时进行活动,那么象棋有 副,跳棋有 副。
17.2075立方厘米= 立方分米
6米5分米= 厘米
15平方千米= 公顷= 平方米
13米4分米= 米
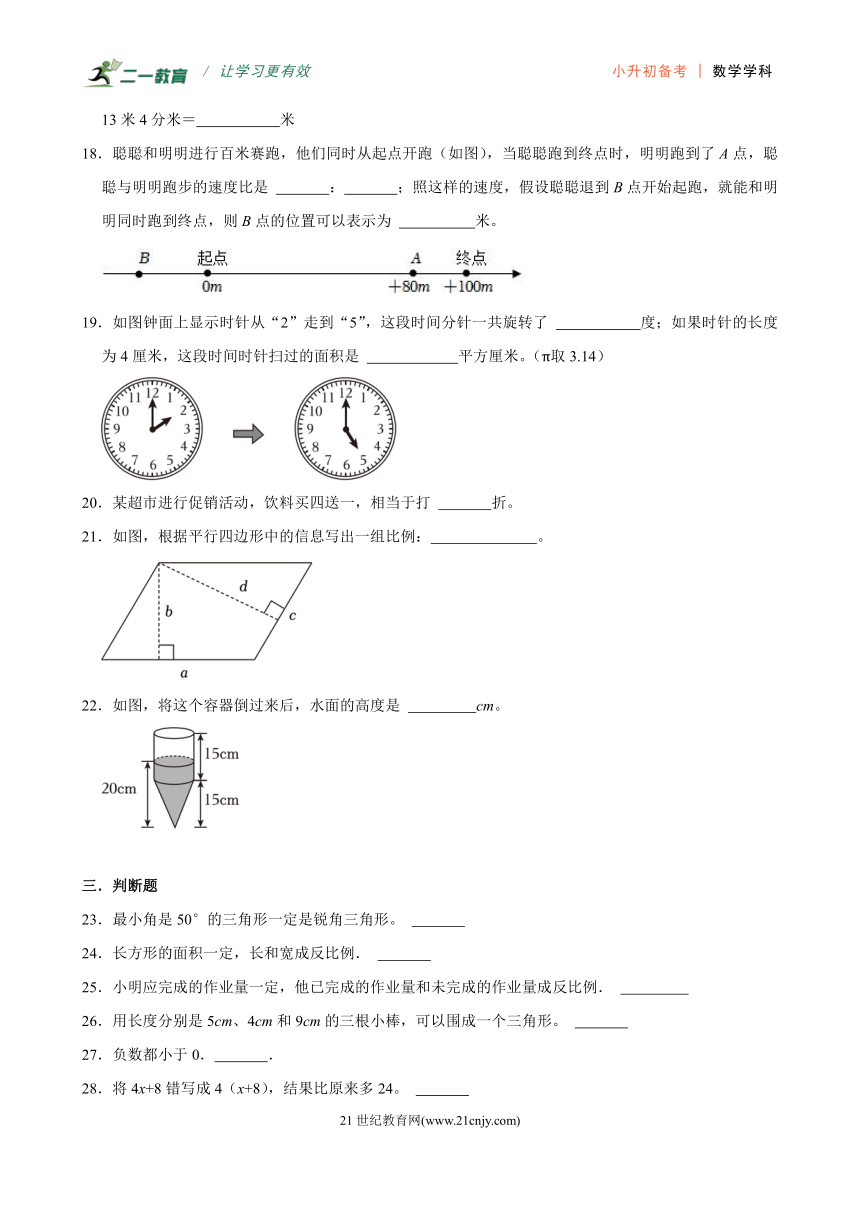
18.聪聪和明明进行百米赛跑,他们同时从起点开跑(如图),当聪聪跑到终点时,明明跑到了A点,聪聪与明明跑步的速度比是 : ;照这样的速度,假设聪聪退到B点开始起跑,就能和明明同时跑到终点,则B点的位置可以表示为 米。
19.如图钟面上显示时针从“2”走到“5”,这段时间分针一共旋转了 度;如果时针的长度为4厘米,这段时间时针扫过的面积是 平方厘米。(π取3.14)
20.某超市进行促销活动,饮料买四送一,相当于打 折。
21.如图,根据平行四边形中的信息写出一组比例: 。
22.如图,将这个容器倒过来后,水面的高度是 cm。
三.判断题
23.最小角是50°的三角形一定是锐角三角形。
24.长方形的面积一定,长和宽成反比例.
25.小明应完成的作业量一定,他已完成的作业量和未完成的作业量成反比例.
26.用长度分别是5cm、4cm和9cm的三根小棒,可以围成一个三角形。
27.负数都小于0. .
28.将4x+8错写成4(x+8),结果比原来多24。
四.计算题
29.解方程或比例。
xx=24 :x:
30.计算下面各题(能简算的要简算)。
4 4.8÷(9.2﹣6.8)×40 (2) 48×101
五.操作题
31.按要求填一填,画一画,算一算。
(1)用数对表示图中D点的位置 。
(2)画出长方形ABCD先向右平移4格,再向上平移3格后的图形。
(3)将原长方形ABCD绕A点逆时针旋转90°,画出旋转后的图形。
(4)画出长方形ABCD按2:1放大后的图形。
六.应用题
32.在六年级组织的爱心义卖活动中,一班共捐义卖款759元,二班比一班少69元,两个班共捐义卖款多少元?
33.欣欣看一本数学故事书,如果每天看15页,需用24天看完。实际每天多看20%,多少天可以看完?(用比例知识解答)
34.妈妈按八折的优惠价格购买了4张《满江红》的电影票,一共花了192元。每张《满江红》电影票的原价是多少元?
35.张明家买了一辆价格为17万元的家用车,按规定需要按所购车辆价格的10%缴纳车辆购置税。张明家买这辆车一共需要花多少万元?
36.“垃圾分类”是一种新时尚,某小区5月份“垃圾分类”情况如图所示。据统计,该小区产生厨余垃圾2吨,产生其它垃圾多少吨?
37.在比例尺是1:20000000的地图上,量得A、B两地的公路线长为4.5厘米。一辆客车和一辆货车同时从两地相对开出,6小时后两车相遇,客车每小时行90千米,货车每小时行多少千米?
参考答案及试题解析
一.选择题
1.【考点】辨识成正比例的量与成反比例的量.
【答案】C
【思路分析】判断方法:关键就看这两种量对应的两个数,是商一定还是积一定,如果商一定,就成正比例;如果积一定,就成反比例。
【解答】解:A.正方形的÷边长=边长,正方形的边长与面积不成比例;
B.圆柱的体积=底面积×高,圆柱的体积一定,它的底面积与高成反比例;
C.比列尺=图上距离:实际距离,比例尺一定,图上距离与实际距离成正比例。
故选:C。
【名师点评】本题考查了辨识成正比例的量和成反比例的量的判断方法。
2.【考点】可能性的大小.
【答案】A
【思路分析】根据题意,8天是晴天,4天是阴天,3天是雨天。从中任选一天,因为8>4>3,所以选中晴天的可能性最大。据此解答即可。
【解答】解:8天是晴天,4天是阴天,3天是雨天。从中任选一天,因为8>4>3,所以选中晴天的可能性最大。
答:选中晴天的可能性最大。
故选:A。
【名师点评】本题考查了可能性大小知识,结合题意分析解答即可。
3.【考点】平均数的含义及求平均数的方法.
【答案】C
【思路分析】四人的平均体重是40.8千克,则四人的总体重是40.8×4=163.2(千克)减去体重最重的和小红的体重后是163.2﹣42﹣38.2=83(千克),即剩下两人的体重和是83千克,据此选择。
【解答】解:40.8×4=163.2(千克)
163.2﹣42﹣38.2=83(千克),即剩下两人的体重和是83千克。
A.39+40=79≠83,不符合题意;
B.40+41=81≠83,不符合题意;
C.41+41=83,符合题意。
故选:C。
【名师点评】本题考查了平均数的应用。
4.【考点】平移.
【答案】A
【思路分析】把一个图形整体沿某一方向移动一定的距离,图形的这种移动,叫做平移,平移后图形的位置改变,形状、大小不变,据此解答即可。
【解答】解:在推导多边形面积时,如图的方法中只用到平移的是。
故选:A。
【名师点评】本题考查了平移知识,结合推导多边形面积的方法,解答即可。
5.【考点】组合图形的面积.
【答案】B
【思路分析】如图所示,把蜘蛛网覆盖的面积分成上、下两个相同的梯形和中间一个长方形,梯形的面积=(上底+下底)×高÷2,长方形的面积=长×宽,蜘蛛网覆盖的面积=梯形的面积×2+长方形的面积,据此解答。
【解答】解:
每个小正方形的面积为1平方单位,则每个小正方形的边长为1个单位。
(2+6)×2÷2×2+6×2
=8×2÷2×2+6×2
=16+12
=28(平方单位)
答:蜘蛛网覆盖的面积是28平方单位。
故选:B。
【名师点评】把所求图形的面积分割成几个基本图形的面积之和是解答题目的关键。
6.【考点】百分数的实际应用.
【答案】C
【思路分析】糖的质量=含糖率×糖水质量,分别求出三杯糖水里面的糖的质量,再除以糖水的总质量即可求出混合糖水的含糖率。
【解答】解:(100×40%+100×47%+100×60%)÷(3×100)×100%
=(40+47+60)÷300×100%
=49%
答:三杯糖水混合在一起后的含糖率是49%。
故选:C。
【名师点评】此题考查含糖率的应用,糖水中糖的质量的求法也是解题的关键。
7.【考点】数与形结合的规律.
【答案】C
【思路分析】观察可知,方框中的圆点数量如,中间空白处圆点数量为4个时,可以符合变化规律,再根据圆点的呈现方式即可选出正确答案。
【解答】解:如图示排列时,具有一定的规律性。
故选:C。
【名师点评】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
8.【考点】百分数的实际应用.
【答案】D
【思路分析】根据票价执行递减递远原则:京沪高铁北京南﹣上海虹桥票价包括两部分,先求出超出1000千米的部分,超出1000千米的部分×收费标准×折扣+500~1000千米的部分×收费标准×折扣+500千米部分×收费标准=票价,据此列式计算。
【解答】解:(1318﹣1000)×0.77×80%+500×0.77×90%+500×0.77
=318×0.77×0.8+385×0.9+385
=195.88+346.5+385
≈927(元)
答:京沪高铁北京南﹣上海虹桥一等座票价四舍五入约是927元。
故选:D。
【名师点评】关键是理解收费规则,理解折扣的意义,几折就是百分之几十。
9.【考点】分数四则复合应用题.
【答案】A
【思路分析】方法一:把袋中原来有米的斗数看作单位“1”,平均分成7份,其中分给关卡的占1份,还剩下的占6份,还剩下5斗米,用5斗米除以剩下的米所占的份数,求出1份量,再乘这袋米的总份数即可求出这袋米原来有多少斗;
方法二:把袋中原来有米的斗数看作单位“1”,剩下的米所占的分率为(1),剩下的米为5斗,根据分数除法的意义,用5斗米除以(1)就是袋中原来有多少斗米。
【解答】解:根据分析得,袋中原来有米斗数:5÷(7﹣1)×7或5÷(1),所以题目中①③的算式都是正确的。
故选:A。
【名师点评】本题主要考查了分数的意义以及分数除法的应用,已知一个数的几分之几是多少,求这个数,用除法计算。
10.【考点】百分数的实际应用.
【答案】D
【思路分析】A4纸是A3纸的一半,A3纸是A2纸的一半,根据此规则,A5纸又是A4纸的一半,设A2纸的面积是1,先把A2纸的面积看成单位“1”,用A2纸的面积乘50%,就是A3纸的面积,同理逐步求出A5纸的面积,再用A5纸的面积除以A2纸的面积即可。
【解答】解:设A2纸的面积是1,
1×50%×50%×50%
=0.25×50%
=0.125
0.125×100%=12.5%
答:A5纸的面积是A2纸的12.5%。
故选:D。
【名师点评】解答此题的关键是分清三个单位“1”的区别,找清各自以谁为标准,再把数据设出,根据基本的数量关系解决问题。
二.填空题
11.【考点】分数的意义和读写;涂色部分表示分数.
【答案】。
【思路分析】假设每个小长方形的长是2,宽是1,观察题意可知,梯形的上底是1,下底是(1×4),高是2,根据梯形的面积公式,用(1+4)×2÷2即可求出梯形的面积;再根据长方形的面积公式,用2×1×4即可求出4个小长方形的面积,再根据求一个数占另一个数的几分之几,用一个数除以另一个数,则用梯形的面积除以4个小长方形的面积,即可求出阴影部分占总面积的几分之几。
【解答】解:假设每个小长方形的长是2,宽是1。
1×4=4
(1+4)×2÷2
=5×2÷2
=5
2×1×4=8
5÷8
阴影部分可以用分数表示为。
故答案为:。
【名师点评】本题主要考查了分数的意义,明确求一个数占另一个数的几分之几,用除法计算。
12.【考点】圆锥的体积;圆柱的特征;圆柱的体积.
【答案】12.56;6;50.24。
【思路分析】根据题意,圆柱的体积公式是:V=Sh,圆锥的体积公式是:VSh,如果把这个圆柱平均截成3段(如图),表面积比原来增加50.24平方厘米,此时一共增加了4个底面的面积,所以圆柱的底面积是50.24÷4=12.56(平方厘米),如果把截成的其中一段捏成一个底面与它相等的圆锥,此时圆锥的体积等于与它等底等高的圆锥体积的3倍,所以此时圆锥的高是截成的一截圆柱的高的3倍,即6厘米。此时圆锥的体积是(立方厘米),截之前圆柱的体积是12.56×6=75.36(立方厘米),所以圆锥的体积比原来未截之前的圆柱体积少75.36﹣25.12=50.24(立方厘米),据此解答。
【解答】解:50.24÷4=12.56(平方厘米)
6÷3×3
=2×3
=6(厘米)
=75.36﹣25.12
=50.24(立方厘米)
答:原来圆柱的底面面积是12.56平方厘米,如果把截成的其中一段捏成一个底面与它相等的圆锥,圆锥的高是6厘米,圆锥的体积比原来未截之前的圆柱体积少50.24立方厘米。
故答案为:12.56;6;50.24。
【名师点评】本题考查了圆柱、圆锥的体积,解决本题的关键是熟练运用圆锥、圆柱的体积公式。
13.【考点】分数乘法应用题.
【答案】14.75。
【思路分析】德州的黑夜时间约是白昼时间的,可以设黑夜的时间是37份,白昼的时间是59份,用白昼时间的份数除以黑夜白昼的时间总份数求出白昼占全天时间的几分之几,再乘24求出具体是多少小时。
【解答】解:59÷(37+59)×24
=59÷96×24
=14.75(小时)
答:夏至这一天德州的白昼时间有14.75小时。
故答案为:14.75。
【名师点评】此题考查分数乘除法的应用,求一个数的几分之几具体是多少用分数乘法。
14.【考点】简单图形的折叠问题.
【答案】297。
【思路分析】观察或动手实践后可知,小阴影三角形是个等腰直角三角形,对折后,阴影部分是个长方形,长方形的宽=原长方形的长﹣原长方形的宽=三角形的直角边,三角形的斜边=原长方形的宽﹣三角形的直角边,据此求出三角形三条边的和即可。
【解答】解:三角形的直角边:297﹣210=87(mm)
三角形的斜边:210﹣87=123(mm)
三角形的周长:87×2+123
=174+123
=297(mm)
答:最后图中小阴影三角形的周长是297mm。
故答案为:297。
【名师点评】关键是具有一定的空间想象能力,也可以用一张A4纸实际折一折,即可发现各边之间的关系。
15.【考点】定义新运算.
【答案】2。
【思路分析】先从25的倍数中找出比2023大且最小的一个,然后计算这个倍数与2023的差。
【解答】解:25△2023
=25×81﹣2023
=2025﹣2023
=2
【名师点评】定义新运算是指用一个符号和已知运算表达式表示一种新的运算。
16.【考点】列方程解含有两个未知数的应用题.
【答案】4,3。
【思路分析】根据“象棋和跳棋共7副”,设跳棋有x副,则象棋有(7﹣x)副;等量关系:下一副跳棋的人数×跳棋的数量+下一副象棋的人数×象棋的数量=总人数,据此列出方程,并求解。
【解答】解:设跳棋有x副,则象棋有(7﹣x)副。
6x+2(7﹣x)=26
6x+14﹣2x=26
4x+14=26
4x=12
x=3
象棋:7﹣3=4(副)
答:象棋有4副,跳棋有3副。
故答案为:4,3。
【名师点评】本题考查列方程解决问题,从题目中找到等量关系,按等量关系列出方程。本题也可以用鸡兔同笼的假设法解答。
17.【考点】小面积单位间的进率及单位换算;大面积单位间的进率及单位换算;体积、容积进率及单位换算;长度的单位换算.
【答案】2.075,650,1500,15000000,13.4。
【思路分析】根据1立方分米=1000立方厘米,1米=100厘米,1米=10分米,1分米=10厘米,1平方千米=100公顷,1公顷=10000平方米,高级单位化低级单位要乘进率,低级单位化高级单位要除以进率,复名数换单名数,单位相同的不用换,单位不同的先统一单位,再加上之前没换单位部分的数,据此解答。
【解答】解:2075立方厘米=2.075立方分米
6米=600厘米
5分米=50厘米
6米5分米=650厘米
15平方千米=1500公顷=15000000平方米
4分米=0.4米
13米4分米=13.4米
故答案为:2.075,650,1500,15000000,13.4。
【名师点评】本题主要考查了体积单位、长度单位、面积单位的换算,明确高级单位化低级单位要乘进率,低级单位化高级单位要除以进率。
18.【考点】简单的行程问题.
【答案】5:4;﹣25。
【思路分析】根据题意,聪聪跑了100m时,明明跑了80m,由于二人跑的时间相同,所以他们的路程比就等于二人的速度比;根据倍比问题的解题思路,用明明跑的路程除以4乘5,可以计算出聪聪跑的路程,再用聪聪跑的路程减去100,可以出B点到起点的距离,由于B点在起点的左面可以用负数表示,所以B点的位置需要用负数表示。
【解答】解:聪聪与明明跑步的速度比是100:80=5:4;
100÷4×5﹣100
=25×5﹣100
=125﹣100
=25(米)
由于B点在起点的左面可以用负数表示,所以B点的位置可以表示为﹣25米。
故答案为:5:4;﹣25。
【名师点评】本题解题关键是理解:由于二人跑的时间相同,所以他们的路程比就等于二人的速度比;根据倍比问题的解题思路,求出聪聪跑的路程,理解正数和负数可以表示相反意义的量。
19.【考点】扇形的面积.
【答案】1080,12.56。
【思路分析】分针每小时旋转360°,时针从“2”走到“5”,共3个小时,据此求出分针一共旋转的度数;时针从“2”走到“5”,共旋转了90°,时针扫过的面积是一个扇形,据此解答时针扫过的面积。
【解答】解:360°×3=1080°
3.14×42
3.14×16
=12.56(平方厘米)
故答案为:1080,12.56。
【名师点评】本题重点考查了扇形面积的计算,需熟记公式。
20.【考点】百分数的实际应用.
【答案】八。
【思路分析】买四送一就是买四个的钱买到五份商品,实际上每份花的钱是原来价钱的五分之四,即80%,也就是相当于打八折。据此解答。
【解答】解:4÷(4+1)
=4÷5
=80%
即相当于打八折。
故答案为:八。
【名师点评】此题考查的是分数应用题的列式,要先找准单位“1”,再据题中的数量关系列式。
21.【考点】比例的意义和基本性质.
【答案】a:c=d:b。(答案不唯一)
【思路分析】根据平行四边形面积=底×高可知:ab=cd,根据比例基本性质可知:a:c=d:b,据此解答。
【解答】解:ab=cd
a:c=d:b(答案不唯一)
故答案为:a:c=b:d。
【名师点评】本题考查的是比例基本性质,理解和应用比例基本性质是解答关键。
22.【考点】组合图形的体积.
【答案】10。
【思路分析】根据圆柱、圆锥的体积公式可知,当圆柱和圆锥等体积等底面积时,圆锥的高是圆柱高的3倍;将容器倒过来后,15cm高的圆锥里的水进入圆柱中,水的体积不变,圆柱和圆锥的底面积也相等,用圆锥中水的高度除以3,即是圆锥中的水进入圆柱中的高度,加上圆柱中原有的一部分高为(20﹣15)cm的水,即是此时水面的高度。据此解答。
【解答】解:15÷3+(20﹣15)
=5+5
=10(厘米)
答:容器倒过来后水面的高度是10厘米。
故答案为:10。
【名师点评】此题主要考查圆柱、圆锥的容积(体积)公式的灵活运用,以及等底等高的圆柱与圆锥体积之间的关系及应用。
三.判断题
23.【考点】三角形的分类.
【答案】√
【思路分析】三角形的内角和是180度,最小的角是50度,另外两个内角的和是180°﹣50°=130°,假设较大的角是51°,那么另一个角就是130°﹣51°=79°,根据三个角的度数判断即可。
【解答】解:假设较大的角是51°,180°﹣50°﹣51°=79°,3个角都是锐角,所以最小角是50°的三角形一定是锐角三角形。原题说法正确。
故答案为:√。
【名师点评】本题考查了三角形内角和的知识及三角形按角分类的方法。
24.【考点】辨识成正比例的量与成反比例的量.
【答案】√
【思路分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
【解答】解:因为长方形的面积=长×宽,
如果长方形的面积一定,即长方形的长和宽的积一定,则长方形的长和宽成反比例.
故答案为:√.
【名师点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
25.【考点】正比例.
【答案】×
【思路分析】根据正反比例的意义,分析数量关系.既然小明应完成的作业量一定,就看那两个变量(他已完成的作业量和未完成的作业量)是比值一定还是乘积一定,从而判定是不是成反比例关系.
【解答】解:已完成的作业量+未完成的作业量=应完成的作业量(一定),
可以看出,已完成的作业量和未完成的作业量是两种相关联的变化的量,但是它们相对应的数是和一定,它们的乘积和比值都不一定,
所以已完成的作业量和未完成的作业量不成任何比例关系.
故答案为:×.
【名师点评】此题重点考查正比例和反比例的意义.
26.【考点】三角形边的关系.
【答案】×
【思路分析】任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边,据此解答。
【解答】解:因为5+4=9厘米,所以用长度是5cm、4cm、9cm的三根小棒,不可以围成一个三角形。原题说法错误。
故答案为:×。
【名师点评】本题考查了三角形的三边关系的应用,结合题意分析解答即可。
27.【考点】正、负数大小的比较.
【答案】见试题解答内容
【思路分析】我们知道,在数轴上,0是正、负数的分界点,负数位于0的左边,正数位于0的右边,在数轴上从左到右的顺序,就是数从小到大的顺序,由此可知,正数大于0和一切负数,0大于一切负数.
【解答】解:正数大于0和一切负数,0大于一切负数,因此题干正确;
故答案为:√
【名师点评】本题是考查正、负数的大小比较.正数大于0和一切负数,0大于一切负数.
28.【考点】用字母表示数.
【答案】√
【思路分析】将两个算式相减即可。
【解答】解:4(x+8)﹣(4x+8)
=4x+32﹣4x﹣8
=24
所以将4x+8错写成4(x+8),结果比原来多24,这句话是正确的。
故答案为:√。
【名师点评】熟练掌握乘法分配律,是解答此题的关键。
四.计算题
29.【考点】分数方程求解.
【答案】x=240;x。
【思路分析】(1)先计算xxx,根据等式的性质,方程两边同时乘10即可求解;
(2)根据比例的性质,转化成x,先计算,再根据等式的性质,方程两边同时乘即可求解。
【解答】(1)xx=24
x=24
x×10=24×10
x=240
(2):x:
x,
x
【名师点评】本题主要考查学生依据等式的性质,以及比例基本性质解方程的能力,解答时注意对齐等号。
30.【考点】分数的四则混合运算;运算定律与简便运算;小数四则混合运算.
【答案】;80;;4848。
【思路分析】(1)、(4)根据乘法分配律进行简算;
(2)、(3)先算小括号里面的减法,再按照从左向右的顺序进行计算。
【解答】解:(1)4
=()
=1
(2)4.8÷(9.2﹣6.8)×40
=4.8÷2.4×40
=2×40
=80
(3)(2)
(4)48×101
=48×(100+1)
=48×100+48×1
=4800+48
=4848
【名师点评】考查了运算定律与简便运算,四则混合运算。注意运算顺序和运算法则,灵活运用所学的运算定律简便计算。
五.操作题
31.【考点】数对与位置;作平移后的图形;作旋转一定角度后的图形;图形的放大与缩小.
【答案】(1)(4,4);
(2)如图:
(3)如图:
(4)如图:
【思路分析】(1)根据利用数对表示物体位置的方法,用数对表示物体的位置时,列数是前,行数在后。据此解答。
(2)根据图形平移的性质,图形平移后图形的形状和大小不变,只是图形的位置发生了变化,据此作图即可。
(2)根据图形旋转的性质,图形旋转后图形的形状和大小不变,只是图形的位置发生了变化,据此作图即可。
(3)根据图形放大的方法,先分别求出放大2倍后,长方形的长、宽各是多少,然后根据长方形的画法画出放大后的图形。
【解答】解:(1)D点的位置用数对表示是(4,4)。
(2)画出长方形ABCD先向右平移4格,再向上平移3格后的图形。作图如下:
(3)将原长方形ABCD绕A点逆时针旋转90°,画出旋转后的图形。作图如下:
(4)画出长方形ABCD按2:1放大后的图形。
3×2=6
2×2=4
作图如下:
故答案为:(4,4)。
【名师点评】此题考查的目的是理解掌握利用数对表示物体位置的方法及应用,图形平移的性质、图形旋转的性质、图形放大的方法及应用。
六.应用题
32.【考点】千以内加减法.
【答案】1449元。
【思路分析】先用759减去69,求出二班捐的义卖款数,再与一班捐的义卖款数相加即可。
【解答】解:759﹣69+759
=690+759
=1449(元)
答:两个班共捐义卖款1449元。
【名师点评】本题考查了利用千以内数的加减解决问题,需准确理解题意。
33.【考点】正、反比例应用题.
【答案】20天。
【思路分析】已知实际每天多看20%,把计划每天看的页数看作单位“1”,实际每天看的页数是计划的(1+20%),用计划每天看的页数×(1+20%),求出实际每天看的页数。再根据每天看的页数×看的天数=这本书的总页数(一定),所以每天看的页数和看的天数成反比例。列式解答即可。
【解答】解:x天可以看完。
15×(1+20%)x=15×24
18x=360
x=20
答:20天可以看完。
【名师点评】本题考查用比例解决实际问题。关键是先根据求一个数的百分之几是多少,用乘法求出实际每天看的页数。再判断题中的两种相关联的量成什么比例。
34.【考点】百分数的实际应用.
【答案】60元。
【思路分析】按八折优惠即原价的80%的价格,用一共用去的钱数除以4,得出1张电影票的价钱,再除以80%,即可得每张电影票原价是多少元。
【解答】解:192÷4÷80%
=48÷80%
=60(元)
答:每张电影票原价是60元。
【名师点评】在商品销售中,打几折,即是按原价的百分之几十出售。
35.【考点】百分数的实际应用.
【答案】18.7万元。
【思路分析】按规定需缴纳10%的车辆购置税,它花钱的总数应是17的(1+10%),运用乘法解答即可。
【解答】解:17×(1+10%)
=17×1.1
=18.7(万元)
答:爸爸买这辆车一共需要花18.7万元。
【名师点评】本题的关键是求出花钱的总数是买车钱数的百分之几,然后根据乘法的意义列式解答。
36.【考点】扇形统计图.
【答案】3.2吨。
【思路分析】把该小区5月份所产生的垃圾看作单位“1”,从扇形统计图可知厨余垃圾占所有垃圾的25%,已知该小区产生厨余垃圾2吨,根据对应量÷对应分率=单位“1”的量,即可求出该小区5月份所产生的垃圾总量;其他垃圾占垃圾总量的40%,根据乘法意义,即可求出其它垃圾多少吨。
【解答】解:2÷25%=8(吨)
8×40%=3.2(吨)
答:产生其它垃圾3.2吨。
【名师点评】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
37.【考点】比例尺应用题.
【答案】60千米/小时。
【思路分析】要求货车每小时行多少千米,先根据“图上距离÷比例尺=实际距离”求出A、B两地的总路程,然后根据“路程÷相遇时间=速度之和”求出两车的速度和,最后用速度和减去客车的速度,即可求出货车的速度。
【解答】解:4.590000000(厘米)
90000000厘米=900千米
900÷6﹣90
=150﹣90
=60(千米/小时)
答:货车每小时行60千米/小时。
【名师点评】此题解题的关键是先根据图上距离、实际距离和比例尺的关系,求出两地的路程,然后根据路程、速度和时间的关系。
21世纪教育网(www.21cnjy.com)
2025年秋六年级数学小升初开学重点校分班摸底培优卷青岛版(六三制)
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题
1.下面选项中两种量成正比例的是( )
A.正方形的边长与面积。
B.圆柱的体积一定,它的底面积与高。
C.比例尺一定,图上距离与实际距离。
2.李爷爷查看15日天气预报,其中8天是晴天,4天是阴天,3天是雨天。从中任选一天,选中( )天的可能性最大。
A.晴 B.阴 C.雨
3.小红所在的小组共4人,体重最重的是42千克,小红最轻是38.2千克,已知她们的平均体重是40.8千克,其他两人的体重可能是( )
A.39 40 B.40 41 C.41 42
4.在推导多边形面积时,如图的方法中只用到平移的是( )
A.
B.
C.
5.一只蜘蛛在纱门上织了一张网(如图),若图中每个小正方形的面积为1平方单位,则蜘蛛网覆盖的面积是( )平方单位。
A.20 B.28 C.36 D.40
6.三杯都是100克的糖水,含糖率分别为40%、47%、60%,三杯糖水混合在一起后的含糖率是( )
A.55% B.50% C.49% D.46%
7.观察图,请选择最适合的一个填入问号处,能使之呈现出一定的规律性的是( )
A. B. C. D.
8.高铁票价的计算取决于线路的速度等级、里程、递远递减以及折扣等方面。京沪高铁线路的票价率及执行原则见下表:
速度等级 线路 起止点 里程(单位:千米) 高铁票价率(单位:元/千米) 备注
二等座 一等座
时速300公里及以上 京沪高速线 北京南﹣上海虹桥 1318 0.46 0.77 票价执行递减递远原则:500千米以下的部分无折扣,500~1000千米的部分打九折,1000~1500千米的部分打八折,以此类推。
据此计算,京沪高铁北京南﹣上海虹桥一等座票价四舍五入约是( )元。
A.554 B.606 C.886 D.927
9.《九章算术》是中国古代的一部数学专著,书中记载了这样一个问题:“有人背一袋米经过关卡,将袋中米的交给关卡后,还剩下5斗米。”袋中原来有多少斗米?正确的列式有( )
①5÷(7﹣1)×7
②5×(1)
③5÷(1)
A.①③ B.②③ C.①②
10.印刷用纸通常用A2、A3、A4、A5等编号表示大小规格,A4纸是A3纸的一半,A5纸是A4纸的一半,按照这样编号规则,A5纸的面积是A2纸的( )
A.20% B.25% C.6.25% D.12.5%
二.填空题
11.如图,阴影部分可以用分数表示为 。
12.丽丽用橡皮泥做了一个高为6厘米的圆柱,如果把这个圆柱平均截成3段(如图),表面积比原来增加50.24平方厘米,原来圆柱的底面面积是 平方厘米,如果把截成的其中一段捏成一个底面与它相等的圆锥,圆锥的高是 厘米,圆锥的体积比原来未截之前的圆柱体积少_______ 立方厘米。
13.中国农历中的夏至是一年中白昼最长、黑夜最短的一天。2023年6月21日这一天是夏至,德州的黑夜时间约是白昼时间的,夏至这一天德州的白昼时间有 小时。
14.A4纸的秘密:一张A4纸,规格是210×297(单位:mm),经过以下两次对折,可以得到如图图形,则最后图中小阴影三角形的周长是 mm。
15.规定运算a△b的结果按照下述方式产生:在a的倍数中找出大于b且最小的一个,计算这个倍数与b的差,如7Δ15=7×3﹣15=6,9Δ6=9×1﹣6=3。那么25△2023= 。
16.实验小学象棋活动室有象棋和跳棋共7副,如果2人下一副象棋,6人下一副跳棋,恰好可供26名学生同时进行活动,那么象棋有 副,跳棋有 副。
17.2075立方厘米= 立方分米
6米5分米= 厘米
15平方千米= 公顷= 平方米
13米4分米= 米
18.聪聪和明明进行百米赛跑,他们同时从起点开跑(如图),当聪聪跑到终点时,明明跑到了A点,聪聪与明明跑步的速度比是 : ;照这样的速度,假设聪聪退到B点开始起跑,就能和明明同时跑到终点,则B点的位置可以表示为 米。
19.如图钟面上显示时针从“2”走到“5”,这段时间分针一共旋转了 度;如果时针的长度为4厘米,这段时间时针扫过的面积是 平方厘米。(π取3.14)
20.某超市进行促销活动,饮料买四送一,相当于打 折。
21.如图,根据平行四边形中的信息写出一组比例: 。
22.如图,将这个容器倒过来后,水面的高度是 cm。
三.判断题
23.最小角是50°的三角形一定是锐角三角形。
24.长方形的面积一定,长和宽成反比例.
25.小明应完成的作业量一定,他已完成的作业量和未完成的作业量成反比例.
26.用长度分别是5cm、4cm和9cm的三根小棒,可以围成一个三角形。
27.负数都小于0. .
28.将4x+8错写成4(x+8),结果比原来多24。
四.计算题
29.解方程或比例。
xx=24 :x:
30.计算下面各题(能简算的要简算)。
4 4.8÷(9.2﹣6.8)×40 (2) 48×101
五.操作题
31.按要求填一填,画一画,算一算。
(1)用数对表示图中D点的位置 。
(2)画出长方形ABCD先向右平移4格,再向上平移3格后的图形。
(3)将原长方形ABCD绕A点逆时针旋转90°,画出旋转后的图形。
(4)画出长方形ABCD按2:1放大后的图形。
六.应用题
32.在六年级组织的爱心义卖活动中,一班共捐义卖款759元,二班比一班少69元,两个班共捐义卖款多少元?
33.欣欣看一本数学故事书,如果每天看15页,需用24天看完。实际每天多看20%,多少天可以看完?(用比例知识解答)
34.妈妈按八折的优惠价格购买了4张《满江红》的电影票,一共花了192元。每张《满江红》电影票的原价是多少元?
35.张明家买了一辆价格为17万元的家用车,按规定需要按所购车辆价格的10%缴纳车辆购置税。张明家买这辆车一共需要花多少万元?
36.“垃圾分类”是一种新时尚,某小区5月份“垃圾分类”情况如图所示。据统计,该小区产生厨余垃圾2吨,产生其它垃圾多少吨?
37.在比例尺是1:20000000的地图上,量得A、B两地的公路线长为4.5厘米。一辆客车和一辆货车同时从两地相对开出,6小时后两车相遇,客车每小时行90千米,货车每小时行多少千米?
参考答案及试题解析
一.选择题
1.【考点】辨识成正比例的量与成反比例的量.
【答案】C
【思路分析】判断方法:关键就看这两种量对应的两个数,是商一定还是积一定,如果商一定,就成正比例;如果积一定,就成反比例。
【解答】解:A.正方形的÷边长=边长,正方形的边长与面积不成比例;
B.圆柱的体积=底面积×高,圆柱的体积一定,它的底面积与高成反比例;
C.比列尺=图上距离:实际距离,比例尺一定,图上距离与实际距离成正比例。
故选:C。
【名师点评】本题考查了辨识成正比例的量和成反比例的量的判断方法。
2.【考点】可能性的大小.
【答案】A
【思路分析】根据题意,8天是晴天,4天是阴天,3天是雨天。从中任选一天,因为8>4>3,所以选中晴天的可能性最大。据此解答即可。
【解答】解:8天是晴天,4天是阴天,3天是雨天。从中任选一天,因为8>4>3,所以选中晴天的可能性最大。
答:选中晴天的可能性最大。
故选:A。
【名师点评】本题考查了可能性大小知识,结合题意分析解答即可。
3.【考点】平均数的含义及求平均数的方法.
【答案】C
【思路分析】四人的平均体重是40.8千克,则四人的总体重是40.8×4=163.2(千克)减去体重最重的和小红的体重后是163.2﹣42﹣38.2=83(千克),即剩下两人的体重和是83千克,据此选择。
【解答】解:40.8×4=163.2(千克)
163.2﹣42﹣38.2=83(千克),即剩下两人的体重和是83千克。
A.39+40=79≠83,不符合题意;
B.40+41=81≠83,不符合题意;
C.41+41=83,符合题意。
故选:C。
【名师点评】本题考查了平均数的应用。
4.【考点】平移.
【答案】A
【思路分析】把一个图形整体沿某一方向移动一定的距离,图形的这种移动,叫做平移,平移后图形的位置改变,形状、大小不变,据此解答即可。
【解答】解:在推导多边形面积时,如图的方法中只用到平移的是。
故选:A。
【名师点评】本题考查了平移知识,结合推导多边形面积的方法,解答即可。
5.【考点】组合图形的面积.
【答案】B
【思路分析】如图所示,把蜘蛛网覆盖的面积分成上、下两个相同的梯形和中间一个长方形,梯形的面积=(上底+下底)×高÷2,长方形的面积=长×宽,蜘蛛网覆盖的面积=梯形的面积×2+长方形的面积,据此解答。
【解答】解:
每个小正方形的面积为1平方单位,则每个小正方形的边长为1个单位。
(2+6)×2÷2×2+6×2
=8×2÷2×2+6×2
=16+12
=28(平方单位)
答:蜘蛛网覆盖的面积是28平方单位。
故选:B。
【名师点评】把所求图形的面积分割成几个基本图形的面积之和是解答题目的关键。
6.【考点】百分数的实际应用.
【答案】C
【思路分析】糖的质量=含糖率×糖水质量,分别求出三杯糖水里面的糖的质量,再除以糖水的总质量即可求出混合糖水的含糖率。
【解答】解:(100×40%+100×47%+100×60%)÷(3×100)×100%
=(40+47+60)÷300×100%
=49%
答:三杯糖水混合在一起后的含糖率是49%。
故选:C。
【名师点评】此题考查含糖率的应用,糖水中糖的质量的求法也是解题的关键。
7.【考点】数与形结合的规律.
【答案】C
【思路分析】观察可知,方框中的圆点数量如,中间空白处圆点数量为4个时,可以符合变化规律,再根据圆点的呈现方式即可选出正确答案。
【解答】解:如图示排列时,具有一定的规律性。
故选:C。
【名师点评】数和图形的规律是相对应的,图形的排列有什么变化规律,数的排列就有相应的变化规律。
8.【考点】百分数的实际应用.
【答案】D
【思路分析】根据票价执行递减递远原则:京沪高铁北京南﹣上海虹桥票价包括两部分,先求出超出1000千米的部分,超出1000千米的部分×收费标准×折扣+500~1000千米的部分×收费标准×折扣+500千米部分×收费标准=票价,据此列式计算。
【解答】解:(1318﹣1000)×0.77×80%+500×0.77×90%+500×0.77
=318×0.77×0.8+385×0.9+385
=195.88+346.5+385
≈927(元)
答:京沪高铁北京南﹣上海虹桥一等座票价四舍五入约是927元。
故选:D。
【名师点评】关键是理解收费规则,理解折扣的意义,几折就是百分之几十。
9.【考点】分数四则复合应用题.
【答案】A
【思路分析】方法一:把袋中原来有米的斗数看作单位“1”,平均分成7份,其中分给关卡的占1份,还剩下的占6份,还剩下5斗米,用5斗米除以剩下的米所占的份数,求出1份量,再乘这袋米的总份数即可求出这袋米原来有多少斗;
方法二:把袋中原来有米的斗数看作单位“1”,剩下的米所占的分率为(1),剩下的米为5斗,根据分数除法的意义,用5斗米除以(1)就是袋中原来有多少斗米。
【解答】解:根据分析得,袋中原来有米斗数:5÷(7﹣1)×7或5÷(1),所以题目中①③的算式都是正确的。
故选:A。
【名师点评】本题主要考查了分数的意义以及分数除法的应用,已知一个数的几分之几是多少,求这个数,用除法计算。
10.【考点】百分数的实际应用.
【答案】D
【思路分析】A4纸是A3纸的一半,A3纸是A2纸的一半,根据此规则,A5纸又是A4纸的一半,设A2纸的面积是1,先把A2纸的面积看成单位“1”,用A2纸的面积乘50%,就是A3纸的面积,同理逐步求出A5纸的面积,再用A5纸的面积除以A2纸的面积即可。
【解答】解:设A2纸的面积是1,
1×50%×50%×50%
=0.25×50%
=0.125
0.125×100%=12.5%
答:A5纸的面积是A2纸的12.5%。
故选:D。
【名师点评】解答此题的关键是分清三个单位“1”的区别,找清各自以谁为标准,再把数据设出,根据基本的数量关系解决问题。
二.填空题
11.【考点】分数的意义和读写;涂色部分表示分数.
【答案】。
【思路分析】假设每个小长方形的长是2,宽是1,观察题意可知,梯形的上底是1,下底是(1×4),高是2,根据梯形的面积公式,用(1+4)×2÷2即可求出梯形的面积;再根据长方形的面积公式,用2×1×4即可求出4个小长方形的面积,再根据求一个数占另一个数的几分之几,用一个数除以另一个数,则用梯形的面积除以4个小长方形的面积,即可求出阴影部分占总面积的几分之几。
【解答】解:假设每个小长方形的长是2,宽是1。
1×4=4
(1+4)×2÷2
=5×2÷2
=5
2×1×4=8
5÷8
阴影部分可以用分数表示为。
故答案为:。
【名师点评】本题主要考查了分数的意义,明确求一个数占另一个数的几分之几,用除法计算。
12.【考点】圆锥的体积;圆柱的特征;圆柱的体积.
【答案】12.56;6;50.24。
【思路分析】根据题意,圆柱的体积公式是:V=Sh,圆锥的体积公式是:VSh,如果把这个圆柱平均截成3段(如图),表面积比原来增加50.24平方厘米,此时一共增加了4个底面的面积,所以圆柱的底面积是50.24÷4=12.56(平方厘米),如果把截成的其中一段捏成一个底面与它相等的圆锥,此时圆锥的体积等于与它等底等高的圆锥体积的3倍,所以此时圆锥的高是截成的一截圆柱的高的3倍,即6厘米。此时圆锥的体积是(立方厘米),截之前圆柱的体积是12.56×6=75.36(立方厘米),所以圆锥的体积比原来未截之前的圆柱体积少75.36﹣25.12=50.24(立方厘米),据此解答。
【解答】解:50.24÷4=12.56(平方厘米)
6÷3×3
=2×3
=6(厘米)
=75.36﹣25.12
=50.24(立方厘米)
答:原来圆柱的底面面积是12.56平方厘米,如果把截成的其中一段捏成一个底面与它相等的圆锥,圆锥的高是6厘米,圆锥的体积比原来未截之前的圆柱体积少50.24立方厘米。
故答案为:12.56;6;50.24。
【名师点评】本题考查了圆柱、圆锥的体积,解决本题的关键是熟练运用圆锥、圆柱的体积公式。
13.【考点】分数乘法应用题.
【答案】14.75。
【思路分析】德州的黑夜时间约是白昼时间的,可以设黑夜的时间是37份,白昼的时间是59份,用白昼时间的份数除以黑夜白昼的时间总份数求出白昼占全天时间的几分之几,再乘24求出具体是多少小时。
【解答】解:59÷(37+59)×24
=59÷96×24
=14.75(小时)
答:夏至这一天德州的白昼时间有14.75小时。
故答案为:14.75。
【名师点评】此题考查分数乘除法的应用,求一个数的几分之几具体是多少用分数乘法。
14.【考点】简单图形的折叠问题.
【答案】297。
【思路分析】观察或动手实践后可知,小阴影三角形是个等腰直角三角形,对折后,阴影部分是个长方形,长方形的宽=原长方形的长﹣原长方形的宽=三角形的直角边,三角形的斜边=原长方形的宽﹣三角形的直角边,据此求出三角形三条边的和即可。
【解答】解:三角形的直角边:297﹣210=87(mm)
三角形的斜边:210﹣87=123(mm)
三角形的周长:87×2+123
=174+123
=297(mm)
答:最后图中小阴影三角形的周长是297mm。
故答案为:297。
【名师点评】关键是具有一定的空间想象能力,也可以用一张A4纸实际折一折,即可发现各边之间的关系。
15.【考点】定义新运算.
【答案】2。
【思路分析】先从25的倍数中找出比2023大且最小的一个,然后计算这个倍数与2023的差。
【解答】解:25△2023
=25×81﹣2023
=2025﹣2023
=2
【名师点评】定义新运算是指用一个符号和已知运算表达式表示一种新的运算。
16.【考点】列方程解含有两个未知数的应用题.
【答案】4,3。
【思路分析】根据“象棋和跳棋共7副”,设跳棋有x副,则象棋有(7﹣x)副;等量关系:下一副跳棋的人数×跳棋的数量+下一副象棋的人数×象棋的数量=总人数,据此列出方程,并求解。
【解答】解:设跳棋有x副,则象棋有(7﹣x)副。
6x+2(7﹣x)=26
6x+14﹣2x=26
4x+14=26
4x=12
x=3
象棋:7﹣3=4(副)
答:象棋有4副,跳棋有3副。
故答案为:4,3。
【名师点评】本题考查列方程解决问题,从题目中找到等量关系,按等量关系列出方程。本题也可以用鸡兔同笼的假设法解答。
17.【考点】小面积单位间的进率及单位换算;大面积单位间的进率及单位换算;体积、容积进率及单位换算;长度的单位换算.
【答案】2.075,650,1500,15000000,13.4。
【思路分析】根据1立方分米=1000立方厘米,1米=100厘米,1米=10分米,1分米=10厘米,1平方千米=100公顷,1公顷=10000平方米,高级单位化低级单位要乘进率,低级单位化高级单位要除以进率,复名数换单名数,单位相同的不用换,单位不同的先统一单位,再加上之前没换单位部分的数,据此解答。
【解答】解:2075立方厘米=2.075立方分米
6米=600厘米
5分米=50厘米
6米5分米=650厘米
15平方千米=1500公顷=15000000平方米
4分米=0.4米
13米4分米=13.4米
故答案为:2.075,650,1500,15000000,13.4。
【名师点评】本题主要考查了体积单位、长度单位、面积单位的换算,明确高级单位化低级单位要乘进率,低级单位化高级单位要除以进率。
18.【考点】简单的行程问题.
【答案】5:4;﹣25。
【思路分析】根据题意,聪聪跑了100m时,明明跑了80m,由于二人跑的时间相同,所以他们的路程比就等于二人的速度比;根据倍比问题的解题思路,用明明跑的路程除以4乘5,可以计算出聪聪跑的路程,再用聪聪跑的路程减去100,可以出B点到起点的距离,由于B点在起点的左面可以用负数表示,所以B点的位置需要用负数表示。
【解答】解:聪聪与明明跑步的速度比是100:80=5:4;
100÷4×5﹣100
=25×5﹣100
=125﹣100
=25(米)
由于B点在起点的左面可以用负数表示,所以B点的位置可以表示为﹣25米。
故答案为:5:4;﹣25。
【名师点评】本题解题关键是理解:由于二人跑的时间相同,所以他们的路程比就等于二人的速度比;根据倍比问题的解题思路,求出聪聪跑的路程,理解正数和负数可以表示相反意义的量。
19.【考点】扇形的面积.
【答案】1080,12.56。
【思路分析】分针每小时旋转360°,时针从“2”走到“5”,共3个小时,据此求出分针一共旋转的度数;时针从“2”走到“5”,共旋转了90°,时针扫过的面积是一个扇形,据此解答时针扫过的面积。
【解答】解:360°×3=1080°
3.14×42
3.14×16
=12.56(平方厘米)
故答案为:1080,12.56。
【名师点评】本题重点考查了扇形面积的计算,需熟记公式。
20.【考点】百分数的实际应用.
【答案】八。
【思路分析】买四送一就是买四个的钱买到五份商品,实际上每份花的钱是原来价钱的五分之四,即80%,也就是相当于打八折。据此解答。
【解答】解:4÷(4+1)
=4÷5
=80%
即相当于打八折。
故答案为:八。
【名师点评】此题考查的是分数应用题的列式,要先找准单位“1”,再据题中的数量关系列式。
21.【考点】比例的意义和基本性质.
【答案】a:c=d:b。(答案不唯一)
【思路分析】根据平行四边形面积=底×高可知:ab=cd,根据比例基本性质可知:a:c=d:b,据此解答。
【解答】解:ab=cd
a:c=d:b(答案不唯一)
故答案为:a:c=b:d。
【名师点评】本题考查的是比例基本性质,理解和应用比例基本性质是解答关键。
22.【考点】组合图形的体积.
【答案】10。
【思路分析】根据圆柱、圆锥的体积公式可知,当圆柱和圆锥等体积等底面积时,圆锥的高是圆柱高的3倍;将容器倒过来后,15cm高的圆锥里的水进入圆柱中,水的体积不变,圆柱和圆锥的底面积也相等,用圆锥中水的高度除以3,即是圆锥中的水进入圆柱中的高度,加上圆柱中原有的一部分高为(20﹣15)cm的水,即是此时水面的高度。据此解答。
【解答】解:15÷3+(20﹣15)
=5+5
=10(厘米)
答:容器倒过来后水面的高度是10厘米。
故答案为:10。
【名师点评】此题主要考查圆柱、圆锥的容积(体积)公式的灵活运用,以及等底等高的圆柱与圆锥体积之间的关系及应用。
三.判断题
23.【考点】三角形的分类.
【答案】√
【思路分析】三角形的内角和是180度,最小的角是50度,另外两个内角的和是180°﹣50°=130°,假设较大的角是51°,那么另一个角就是130°﹣51°=79°,根据三个角的度数判断即可。
【解答】解:假设较大的角是51°,180°﹣50°﹣51°=79°,3个角都是锐角,所以最小角是50°的三角形一定是锐角三角形。原题说法正确。
故答案为:√。
【名师点评】本题考查了三角形内角和的知识及三角形按角分类的方法。
24.【考点】辨识成正比例的量与成反比例的量.
【答案】√
【思路分析】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例.
【解答】解:因为长方形的面积=长×宽,
如果长方形的面积一定,即长方形的长和宽的积一定,则长方形的长和宽成反比例.
故答案为:√.
【名师点评】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再做判断.
25.【考点】正比例.
【答案】×
【思路分析】根据正反比例的意义,分析数量关系.既然小明应完成的作业量一定,就看那两个变量(他已完成的作业量和未完成的作业量)是比值一定还是乘积一定,从而判定是不是成反比例关系.
【解答】解:已完成的作业量+未完成的作业量=应完成的作业量(一定),
可以看出,已完成的作业量和未完成的作业量是两种相关联的变化的量,但是它们相对应的数是和一定,它们的乘积和比值都不一定,
所以已完成的作业量和未完成的作业量不成任何比例关系.
故答案为:×.
【名师点评】此题重点考查正比例和反比例的意义.
26.【考点】三角形边的关系.
【答案】×
【思路分析】任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边,据此解答。
【解答】解:因为5+4=9厘米,所以用长度是5cm、4cm、9cm的三根小棒,不可以围成一个三角形。原题说法错误。
故答案为:×。
【名师点评】本题考查了三角形的三边关系的应用,结合题意分析解答即可。
27.【考点】正、负数大小的比较.
【答案】见试题解答内容
【思路分析】我们知道,在数轴上,0是正、负数的分界点,负数位于0的左边,正数位于0的右边,在数轴上从左到右的顺序,就是数从小到大的顺序,由此可知,正数大于0和一切负数,0大于一切负数.
【解答】解:正数大于0和一切负数,0大于一切负数,因此题干正确;
故答案为:√
【名师点评】本题是考查正、负数的大小比较.正数大于0和一切负数,0大于一切负数.
28.【考点】用字母表示数.
【答案】√
【思路分析】将两个算式相减即可。
【解答】解:4(x+8)﹣(4x+8)
=4x+32﹣4x﹣8
=24
所以将4x+8错写成4(x+8),结果比原来多24,这句话是正确的。
故答案为:√。
【名师点评】熟练掌握乘法分配律,是解答此题的关键。
四.计算题
29.【考点】分数方程求解.
【答案】x=240;x。
【思路分析】(1)先计算xxx,根据等式的性质,方程两边同时乘10即可求解;
(2)根据比例的性质,转化成x,先计算,再根据等式的性质,方程两边同时乘即可求解。
【解答】(1)xx=24
x=24
x×10=24×10
x=240
(2):x:
x,
x
【名师点评】本题主要考查学生依据等式的性质,以及比例基本性质解方程的能力,解答时注意对齐等号。
30.【考点】分数的四则混合运算;运算定律与简便运算;小数四则混合运算.
【答案】;80;;4848。
【思路分析】(1)、(4)根据乘法分配律进行简算;
(2)、(3)先算小括号里面的减法,再按照从左向右的顺序进行计算。
【解答】解:(1)4
=()
=1
(2)4.8÷(9.2﹣6.8)×40
=4.8÷2.4×40
=2×40
=80
(3)(2)
(4)48×101
=48×(100+1)
=48×100+48×1
=4800+48
=4848
【名师点评】考查了运算定律与简便运算,四则混合运算。注意运算顺序和运算法则,灵活运用所学的运算定律简便计算。
五.操作题
31.【考点】数对与位置;作平移后的图形;作旋转一定角度后的图形;图形的放大与缩小.
【答案】(1)(4,4);
(2)如图:
(3)如图:
(4)如图:
【思路分析】(1)根据利用数对表示物体位置的方法,用数对表示物体的位置时,列数是前,行数在后。据此解答。
(2)根据图形平移的性质,图形平移后图形的形状和大小不变,只是图形的位置发生了变化,据此作图即可。
(2)根据图形旋转的性质,图形旋转后图形的形状和大小不变,只是图形的位置发生了变化,据此作图即可。
(3)根据图形放大的方法,先分别求出放大2倍后,长方形的长、宽各是多少,然后根据长方形的画法画出放大后的图形。
【解答】解:(1)D点的位置用数对表示是(4,4)。
(2)画出长方形ABCD先向右平移4格,再向上平移3格后的图形。作图如下:
(3)将原长方形ABCD绕A点逆时针旋转90°,画出旋转后的图形。作图如下:
(4)画出长方形ABCD按2:1放大后的图形。
3×2=6
2×2=4
作图如下:
故答案为:(4,4)。
【名师点评】此题考查的目的是理解掌握利用数对表示物体位置的方法及应用,图形平移的性质、图形旋转的性质、图形放大的方法及应用。
六.应用题
32.【考点】千以内加减法.
【答案】1449元。
【思路分析】先用759减去69,求出二班捐的义卖款数,再与一班捐的义卖款数相加即可。
【解答】解:759﹣69+759
=690+759
=1449(元)
答:两个班共捐义卖款1449元。
【名师点评】本题考查了利用千以内数的加减解决问题,需准确理解题意。
33.【考点】正、反比例应用题.
【答案】20天。
【思路分析】已知实际每天多看20%,把计划每天看的页数看作单位“1”,实际每天看的页数是计划的(1+20%),用计划每天看的页数×(1+20%),求出实际每天看的页数。再根据每天看的页数×看的天数=这本书的总页数(一定),所以每天看的页数和看的天数成反比例。列式解答即可。
【解答】解:x天可以看完。
15×(1+20%)x=15×24
18x=360
x=20
答:20天可以看完。
【名师点评】本题考查用比例解决实际问题。关键是先根据求一个数的百分之几是多少,用乘法求出实际每天看的页数。再判断题中的两种相关联的量成什么比例。
34.【考点】百分数的实际应用.
【答案】60元。
【思路分析】按八折优惠即原价的80%的价格,用一共用去的钱数除以4,得出1张电影票的价钱,再除以80%,即可得每张电影票原价是多少元。
【解答】解:192÷4÷80%
=48÷80%
=60(元)
答:每张电影票原价是60元。
【名师点评】在商品销售中,打几折,即是按原价的百分之几十出售。
35.【考点】百分数的实际应用.
【答案】18.7万元。
【思路分析】按规定需缴纳10%的车辆购置税,它花钱的总数应是17的(1+10%),运用乘法解答即可。
【解答】解:17×(1+10%)
=17×1.1
=18.7(万元)
答:爸爸买这辆车一共需要花18.7万元。
【名师点评】本题的关键是求出花钱的总数是买车钱数的百分之几,然后根据乘法的意义列式解答。
36.【考点】扇形统计图.
【答案】3.2吨。
【思路分析】把该小区5月份所产生的垃圾看作单位“1”,从扇形统计图可知厨余垃圾占所有垃圾的25%,已知该小区产生厨余垃圾2吨,根据对应量÷对应分率=单位“1”的量,即可求出该小区5月份所产生的垃圾总量;其他垃圾占垃圾总量的40%,根据乘法意义,即可求出其它垃圾多少吨。
【解答】解:2÷25%=8(吨)
8×40%=3.2(吨)
答:产生其它垃圾3.2吨。
【名师点评】此题考查的目的是理解掌握扇形统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题。
37.【考点】比例尺应用题.
【答案】60千米/小时。
【思路分析】要求货车每小时行多少千米,先根据“图上距离÷比例尺=实际距离”求出A、B两地的总路程,然后根据“路程÷相遇时间=速度之和”求出两车的速度和,最后用速度和减去客车的速度,即可求出货车的速度。
【解答】解:4.590000000(厘米)
90000000厘米=900千米
900÷6﹣90
=150﹣90
=60(千米/小时)
答:货车每小时行60千米/小时。
【名师点评】此题解题的关键是先根据图上距离、实际距离和比例尺的关系,求出两地的路程,然后根据路程、速度和时间的关系。
21世纪教育网(www.21cnjy.com)
同课章节目录
