(小升初开学分班考)小升初开学重点校分班摸底押题卷-2025年秋六年级数学青岛版(六三学制)(含答案解析)
文档属性
| 名称 | (小升初开学分班考)小升初开学重点校分班摸底押题卷-2025年秋六年级数学青岛版(六三学制)(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 255.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-16 12:48:10 | ||
图片预览




文档简介
/ 让学习更有效 小升初备考 | 数学学科
2025年秋六年级数学小升初开学重点校分班摸底押题卷青岛版(六三制)
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题
1.再添一个小正方形,使它成为一个正方体的展开图,添加的方法共有( )种。
A.3 B.4 C.5
2.把一根4米长的绳子平均分成m段,每段长( )米。
A. B. C. D.
3.数轴上有四个点分别是,﹣1,+2,其中( )更接近0。
A. B. C.﹣1 D.+2
4.三位同学进行小组研究学习,各自表达自己的思路和方法,合理的是( )
A.①②③ B.①② C.②③ D.①③
5.移动公司进行技能大比拼,一件工作,张叔叔单独做8分钟完成,李叔叔单独做10分钟完成,那么下列说法不成立的是( )
A.张叔叔的工作效率和工作时间成正比例
B.李叔叔5天做的工作量,张叔叔只需4天
C.张叔叔用时比李叔叔节省
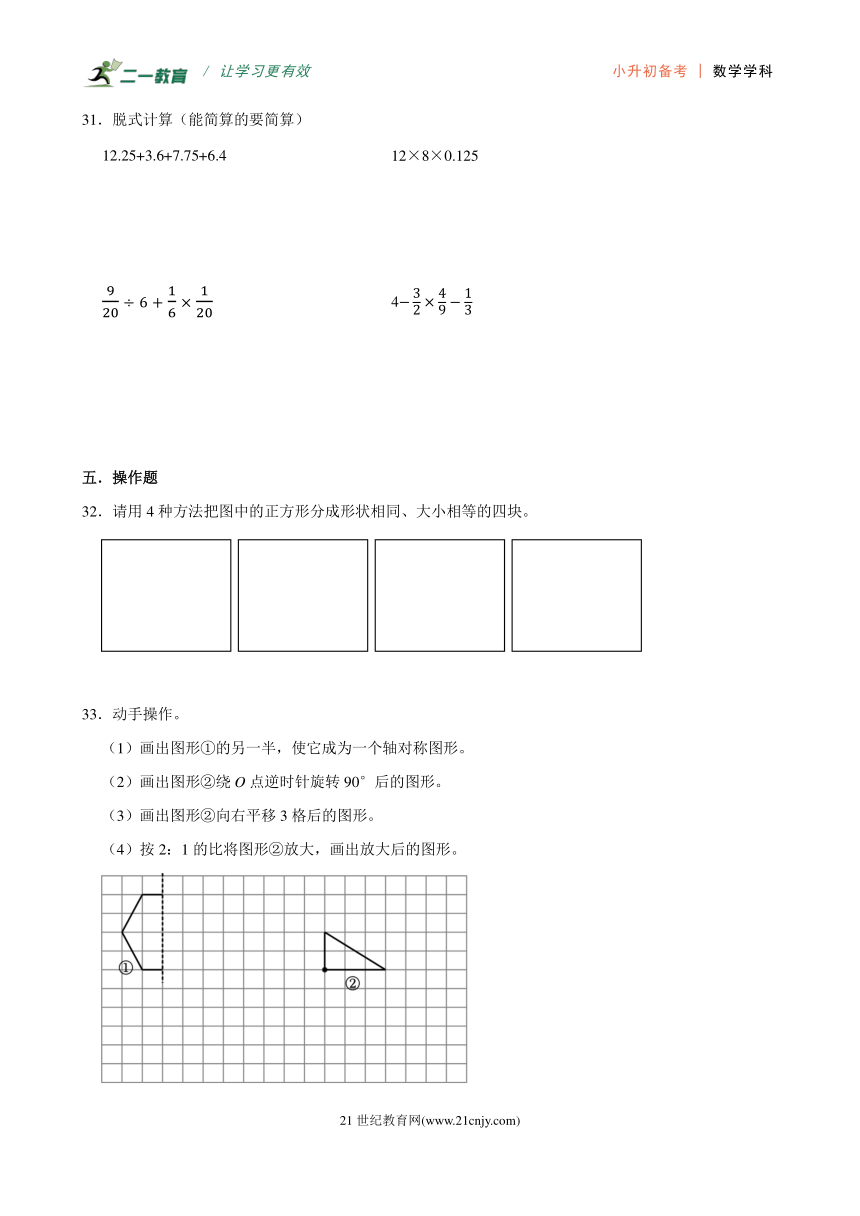
D.李叔叔的工作效率比张叔叔低20%
6.毕业赠礼物,为了分类摆放提高效率,将4个完全一样的长方体礼物盒子包成一包,扎物盒子的长是10cm,宽是6cm,高是4cm,下面最省包装纸的是( )
A. B. C. D.
7.六年级一周30节课,要反映各学科课时与总课时之间的关系,选择( )比较合适。
A.条形统计图 B.折线统计图 C.扇形统计图
8.一种机器零件,横截面是环形,外直径是8毫米,画在图纸上的长度是4厘米。这张图纸的比例尺是(( )
A.5:1 B.2:1 C.1:2
9.从这四张数字卡片中任选两张,组成不同的两位数。其中3和5的公倍数有( )个。
A.2 B.3 C.4
10.用一张正方形纸卷成一个圆柱形纸筒,这个圆柱体纸筒的底面直径和高的比是( )
A.π:1 B.1:π C.2π:1
二.填空题
11.小强用三根整厘米的小棒拼一个三角形,其中两根小棒的长度分别是5厘米和6厘米,第三根小棒的长度最长是 厘米。
12.一个三角形,它的一个内角度数占内角和的,其余两个角是按剩下度数的2:3来分配的。这个三角形是 三角形。
13.2023年“五一”假期,全国国内旅游出游二亿七千四百万人次,横线上的数写作 人次;实现国内旅游收入148056000000元,省略亿后面的尾数是 亿元。
14.2023年5月10日,第三期和第四期储蓄国债开始发行,其中第三期限期二年,年利率是2.95%,爸爸买了50000元第三期国债,到期时的利息是 元。
15.和都是假分数,的分数单位是 ;如果A是一个合数,那么A表示的数字是 。
16.青岛到杭州全程813.4千米,合 千米 米。一列客车上午7:30从青岛出发,下午3:30到达杭州,这列客车途中共用 小时。
17.实验室有如右图的两个容器,吴老师将2L的药水倒入两个容器中,刚好倒完,两个容器都刚好倒满。已知两个容器的底面积相等,则圆锥形容器的容积是 L。
18.小丽将一张纸对折后,剪出了一个符合轴对称的三角形,将三角形完全展开后,经测量发现其中两条边的长度分别是7厘米和15厘米,如果不考虑小数的情况,另外一条边是 厘米。
19.3吨70千克= 千克 7.5立方米= 升
20.把4千克糖果平均分成8包,每包重 千克,每包占4千克的 。
21.一根底面直径是4分米、高是5分米的圆柱形木材,如果把它截成3段,表面积会增加 平方分米;如果把它沿底面直径切成形状、大小完全相同的两部分,表面积会增加 平方分米。
22.比萨斜塔高54.5米,按1:100的比例尺画出它的平面图,高是 厘米。
三.判断题
23.圆规两脚间的距离是4厘米,画出的圆的周长是12.56厘米。
24.圆柱的体积比与它等底等高的圆锥的体积多. .
25.两条直线相交组成的四个角中如果有一个角是直角,那么其它三个角也是直角. .
26.xyz,那么x、y、z的关系是x>y>z.
27.一个长方形,长增加3米,宽增加4米,它的面积就增加12平方米.
28.一个等腰三角形,两角之和是130°,则两角之差是30°。
四.计算题
29.直接写出得数。
0.4+0.66= 5÷0.05= 6.3﹣2.7= 0.25×0.4= 1
3 33= 3×0
30.解方程或比例。
3x﹣0.5x=1.6
31.脱式计算(能简算的要简算)
12.25+3.6+7.75+6.4 12×8×0.125
4
五.操作题
32.请用4种方法把图中的正方形分成形状相同、大小相等的四块。
33.动手操作。
(1)画出图形①的另一半,使它成为一个轴对称图形。
(2)画出图形②绕O点逆时针旋转90°后的图形。
(3)画出图形②向右平移3格后的图形。
(4)按2:1的比将图形②放大,画出放大后的图形。
六.应用题
34.青岛电视塔的塔蝶直径为32米,塔蝶之上的环形露天观光平台的宽度是4.5米。环形露天观光平台的面积是多少?
35.一个圆柱的底面周长和高相等,如果高增加4cm,表面积就增加125.6cm2,原来这个圆柱的表面积是多少平方厘米?
36.测量小组测量教学楼的影子长是22.5米,同时量得附近一个3米高的篮球架的影子长是4.5米,教学楼高多少米?(用比例知识解答)
37.甲乙两车分别从AB两城相对开出。甲车2小时行驶了160千米,甲乙车的速度比是4:3,两车行驶了4.2小时相遇。AB两城相距多少千米?
38.甲、乙两地相距150千米,在一幅地图上量得甲、乙两地之间的距离是5厘米,同时在这幅地图上量得乙、丙两地之间的距离是7厘米,乙、丙两地之间的实际距离是多少千米?(用比例解)
39.可乐家新买一圆柱形鱼缸,测得缸体直径36厘米等数据如图所示:
(1)这个鱼缸的占地面积是多少平方厘米?
(2)鱼缸缸体侧面是透明玻璃制成,这个圆柱形鱼缸需要多少玻璃?
(3)水族界有个比较公认的算法:一升水大约能养1厘米长的一条鱼,比如10升水就大约能养10厘米长的一条鱼或者养1厘米长的10条鱼。那么这个鱼缸大约能养多少条5厘米长的鱼?
参考答案及试题解析
一.选择题
1.【考点】正方体的展开图.
【答案】B
【思路分析】根据正方体展开图的11种特征,再下层的任一个正方形的正面再画一个相同的正方形,即可使之成为一个正方体展开图的“1﹣4﹣1”型。
【解答】解:如图:
再添一个小正方形,使它成为一个正方体的展开图,添加的方法共有4种。
故选:B。
【名师点评】此题是考查正方体展开图的认识。正方体展开图分四种类型,11种情况,要掌握每种情况的特征。
2.【考点】分数除法应用题.
【答案】D
【思路分析】求每段长多少米,是把4米平均分成m份,所以用这根绳子的长度除以平均分成的段数就是每段的长度。
【解答】解:4÷m(米)
答:每段长米。
故选:D。
【名师点评】解决此题关键是弄清求的是“分率”还是“具体的数量”,求分率:平均分的是单位“1”;求具体的数量:平均分的是具体的数量,要注意:分率不能带单位名称,而具体的数量要带单位名称。
3.【考点】数轴的认识;正、负数大小的比较.
【答案】B
【思路分析】根据题意,与0相差,与0相差,﹣1与0相差1,+2与0相差2,据此比较解答即可。
【解答】解:与0相差,与0相差,﹣1与0相差1,+2与0相差2,
因为1<2,所以更接近0。
故选:B。
【名师点评】本题考查了数轴知识,结合比较大小的方法解答即可。
4.【考点】数学常识.
【答案】D
【思路分析】根据题意,①中竖式计算12÷5时,余下的2表示2个一,后面添上0后,表示20个十分之一,据此分析即可;
②中22×9÷2,据此分析即可;
③中(1)×(2)=(1×2)×(),据此解答即可。
【解答】解:①中竖式计算12÷5时,余下的2表示2个一,后面添上0后,表示20个十分之一,所以原说法正确;
②中22×9÷2,所以原说法错误;
③中(1)×(2)=(1×2)×(),所以原说法正确。
所以三位同学进行小组研究学习,各自表达自己的思路和方法,合理的是①③。
故选:D。
【名师点评】本题考查了除法竖式计算以及分数乘除法计算的算理知识,结合题意分析解答即可。
5.【考点】辨识成正比例的量与成反比例的量;百分数的实际应用;简单的工程问题.
【答案】A
【思路分析】先根据“工作量=工作效率×工作时间”,直接判断选项A的说法是否正确;再将工作量设为1,由题意可知,张叔叔单独做每分钟完成,李叔叔单独做每分钟完成。据此计算后判断B、C、D的说法是否正确。
【解答】解:选项A,工作量=工作效率×工作时间,这件工作的工作量一定,张叔叔的工作效率和工作时间成反比例。原题说法错误;
选项B,5
=4(天)
答:李叔叔5天做的工作量,张叔叔只需4天。
原题说法正确;
选项C,(10﹣8)÷10
=2÷10
答:张叔叔用时比李叔叔节省。
原题说法正确;
选项D,()
=0.2
=20%
答:李叔叔的工作效率比张叔叔低20%。
原题说法正确。
故选:A。
【名师点评】解答本题需明确成正比例和成反比例的判定方法,熟练掌握工作量、工作时间和工作效率之间的关系,熟记求一个数比另一个数多(少)几分之几或百分之几的计算方法。
6.【考点】长方体和正方体的表面积.
【答案】C
【思路分析】根据长方体表面积的意义可知,要想最节省包装纸,也就是把4个完全一样的长方体礼品盒的最大面重合摞起来进行包装,据此解答即可。
【解答】解:要想最节省包装纸,也就是把4个完全一样的长方体礼品盒的最大面重合摞起来进行包装。
故选:C。
【名师点评】此题考查的目的是理解掌握长方体表面积的意义及应用。
7.【考点】统计图的选择.
【答案】C
【思路分析】首先要清楚每一种统计图的优点:条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【解答】解:六年级一周30节课,要反映各学科课时与总课时之间的关系,选择扇形比较合适。
故选:C。
【名师点评】解答此题要熟练掌握统计图的特点,根据实际情况灵活选择。
8.【考点】比例尺.
【答案】A
【思路分析】图上距离:实际距离=比例尺,据此代入数据解答即可。
【解答】解:4厘米:8毫米
=40毫米:8毫米
=40:8
=5:1
答:这张图纸的比例尺是5:1。
故选:A。
【名师点评】熟练掌握比例尺的意义是解题的关键。
9.【考点】公倍数和最小公倍数.
【答案】A
【思路分析】根据题意,组成的两位数是:10、30、50、13、31、15、51、35、53,这些数中只有30和15是3和5的公倍数。
【解答】解:从0、1、3、5这四张数字卡片中任选两张,组成不同的两位数。其中3和5的公倍数有2个,分别是15和30。
故答案为:A。
【名师点评】此题考查了数的组成和3和5的公倍数,要求学生掌握。
10.【考点】比的意义;圆柱的展开图.
【答案】B
【思路分析】用一张正方形纸围成一个圆柱形纸筒,圆柱的底面周长等于正方形的边长,圆柱的高等于正方形的边长,据此判断选择即可。
【解答】解:设这个正方形的边长为a,则圆柱的底面周长等于a,圆柱的高等于a,则这个圆柱体纸筒的底面直径和高的比是
(a÷π):a=1:π
故选:B。
【名师点评】解答本题的关键是明确:圆柱的底面周长等于正方形的边长,圆柱的高等于正方形的边长。
二.填空题
11.【考点】三角形边的关系;三角形的特性.
【答案】10。
【思路分析】任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边,据此解答。
【解答】解:5+6=11(厘米)
11﹣1=10(厘米)
答:第三根小棒的长度最长是10厘米。
故答案为:10。
【名师点评】本题考查了三角形的三边关系的应用。
12.【考点】按比例分配应用题;三角形的分类.
【答案】直角。
【思路分析】把内角和180度看作单位“1“,用180°乘,求出它的一个内角度数,再用180°减去它的一个内角度数,求出其余两个角的度数和,又知道其余两个角是按剩下度数的2:3来分配的。再用其余两个角的度数和除以(2+3),求出一份是多少度,再分别乘2、3求出其余两个角各是多少度,再判断三角形的类型。
【解答】解:180°30°
(180°﹣30°)×(2+3)
=150°÷5
=30°
30°×2=60°
30°×3=90°
有一个角是直角90°,所以这个三角形是等腰直角三角形。
答:这个三角形是直角三角形。
故答案为:直角。
【名师点评】本题考查了三角形的类型、内角和和按比例分配问题。
13.【考点】亿以上数的读写;亿以上数的改写与近似.
【答案】见试题解答内容
【思路分析】根据整数的写法,从高位到低位,一级一级地写,哪一个数位上一个计数单位也没有,就在那个数位上写0,即可写出此数;省略“亿”后面的尾数就是四舍五入到亿位,就是把亿位后的千万位上的数进行四舍五入,再在数的后面写上“亿”字。
【解答】解:二亿七千四百万写作:274000000;148056000000≈1481亿。
故答案为:274000000,1481。
【名师点评】本题主要考查整数的写法和求近似数,分级写或借助数位表写数能较好的避免写错数的情况,求近似数时要注意带计数单位。
14.【考点】存款利息与纳税相关问题.
【答案】2950元。
【思路分析】取出的钱数=买国债用的钱数×年利率×年数,结合已知数据,列式计算,求出取出的钱数即可。
【解答】解:50000×2.95%×2
=100000×0.0295
=2950(元)
答:到期时的利息是2950元。
故答案为:2950元。
【名师点评】本题是一道关于百分数应用的题目,解答本题的关键是掌握取出的钱数的计算方法。
15.【考点】分数的意义和读写;用字母表示数.
【答案】,6。
【思路分析】分数单位是把单位“1”平均分成若干份,表示其中的一份的数;假分数就是分子大于分母(或等于分母)的数;合数是在大于1的整数中,除了能被1和本身整除外,还能被其他数(0除外)整除的数。
【解答】解:和都是假分数,的分数单位是,如果A是一个合数,那么A表示的数字是6。
故答案为:,6。
【名师点评】此题考查了假分数、分数单位以及合数的知识,要求学生掌握。
16.【考点】日期和时间的推算.
【答案】见试题解答内容
【思路分析】1千米=1000米,根据低级单位换算成高级单位用除法计算,高级单位换算成低级单位用乘法计算完成填空。
运用结束时刻﹣开始时刻=经过的时间。
【解答】解:813.4千米,合813千米400米。
下午3:30=15时30分
15时30分﹣7时30分=8小时
故答案为:813,400;8。
【名师点评】本题考查时间的推算及长度单位之间的换算,要牢记这些单位之间的进率和换算规则。
17.【考点】圆锥的体积.
【答案】0.5。
【思路分析】因为等底等高的圆柱的体积是圆锥体积的3倍,所以等底等高的圆柱与圆锥的体积和相当于圆锥体积的(3+1)倍,根据已知一个数的几倍是多少,求这个数,用除法解答。
【解答】解:2÷(3+1)
=2÷4
=0.5(升)
答:圆锥形容器的容积是0.5升。
故答案为:0.5。
【名师点评】此题考查的目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及应用。
18.【考点】简单图形的折叠问题.
【答案】15。
【思路分析】根据剪成的三角形符合轴对称的三角形,可知这是一个等腰三角形,在三角形中。两边之和要大于第三边,如果7厘米是腰长,7+7<15,所以不符合三角形边的规律,据此可知另一条腰长是15厘米。据此解答即可。
【解答】解:7+7<15
15+15>7
所以另外一条边是15厘米。
故答案为:15。
【名师点评】本题考查三角形边的关系。
19.【考点】体积、容积进率及单位换算;质量的单位换算.
【答案】3070,7500。
【思路分析】把3吨乘进率1000化成3000千克再加70千克。
高级单位立方米化低级单位升乘进率1000。
【解答】解:3吨70千克=3070千克
7.5立方米=7500升
故答案为:3070,7500。
【名师点评】此题是考查质量的单位换算、体积(容积)的单位换算。单位换算首先要弄清是由高级单位化低级单位还是由低级单位化高级单位,其次记住单位间的进率。
20.【考点】分数的意义和读写.
【答案】。
【思路分析】根据题意,求每包重多少千克,利用总质量除以包数即可,求每包占总质量的几分之几,利用1除以8即可。
【解答】解:4(千克)
1
答:每包重千克,每包占4千克的。
故答案为:。
【名师点评】本题考查了分数的意义及应用。
21.【考点】圆柱的侧面积、表面积和体积;简单的立方体切拼问题.
【答案】50.24,40。
【思路分析】根据题意可知,把这根圆柱形木料横截成3段,表面积增加4个底面的面积;如果把它沿底面直径切成形状、大小完全相同的两部分,表面积会增加两个切面的面积,每个切面的长等于圆柱的高,每个切面的宽等于圆柱的底面直径,根据圆的面积公式:S=πr2,长方形的面积公式:S=ab,把数据代入公式解答。
【解答】解:3.14×(4÷2)2×4
=3.14×4×4
=12.56×4
=50.24(平方分米)
5×4×2
=20×2
=40(平方分米)
答:如果把它截成3段,表面积会增加50.24平方分米,如果把它沿底面直径切成形状、大小完全相同的两部分,表面积会增加40平方分米。
故答案为:50.24,40。
【名师点评】此题考查的目的是理解掌握圆柱表面积的意义及应用,圆的面积公式、长方形的面积公式及应用。
22.【考点】图上距离与实际距离的换算(比例尺的应用).
【答案】54.5。
【思路分析】图上距离=实际距离×比例尺,据此代入数据解答即可。
【解答】解:54.5米=5450厘米
545054.5(厘米)
答:高是54.5厘米。
故答案为:54.5。
【名师点评】熟练掌握比例尺、图上距离、实际距离三者间的关系是解题的关键。
三.判断题
23.【考点】圆、圆环的周长.
【答案】×
【思路分析】用圆规画圆时,圆规两脚间的距离是4厘米,画出圆的半径是4厘米,根据圆的周长公式:C=2πr,把数据代入公式解答。
【解答】解:3.14×4×2
=3.14×8
=25.12(厘米)
答:画出的圆的周长是25.12厘米。
所以原题说法是错误的。
故答案为:×。
【名师点评】此题主要考查圆周长公式的灵活运用,关键是熟记公式。
24.【考点】圆锥的体积.
【答案】见试题解答内容
【思路分析】因为一个圆柱的体积是与它等底等高的圆锥体积的3倍,所以圆柱体积比与它等底等高的圆锥体积大2倍.
【解答】解:因为一个圆柱的体积是与它等底等高的圆锥体积的3倍,
所以圆柱体积比与它等底等高的圆锥体积大:(3﹣1)÷1=2倍.
故答案为:×.
【名师点评】此题是考查圆柱、圆锥的关系,要注意圆柱和圆锥在等底等高的条件下体积有3倍或的关系.
25.【考点】垂直与平行的特征及性质.
【答案】见试题解答内容
【思路分析】两条直线相交,有两种情况,垂直或不垂直,如果其中一个角是90°,那么其它各个角都是90°,这两条直线就相互垂直.
【解答】解:由垂直的含义可知:两条直线相交组成的四个角中如果有一个角是直角,那么其它三个角也是直角,
所以原题说法正确;
故答案为:√.
【名师点评】此题考查了垂直的含义,注意对一些基础概念和性质的理解.
26.【考点】分数的大小比较.
【答案】×
【思路分析】已知xyz,由它们的和相等,一个加数大另一个加数就小,比较加数的大小,即可得出另一个加数的大小,再判断即可.
【解答】解:
,
所以
所以x<y<z;
故答案为:×.
【名师点评】此题考查了两个加数与和之间的关系.
27.【考点】长方形、正方形的面积.
【答案】×
【思路分析】根据长方形的面积公式:S=ab,长方形长和宽增加后,又形成了三个长方形,三个长方形的面积和即为增加的面积,据此可列式推算判断即可.
【解答】解:如图:
则增加的面积为:4a+3b+4×3=4a+3b+12
因a、b不能为0,所以4a+3b+12>12
所以一个长方形,长增加3米,宽增加4米,它的面积就增加12平方米.这种说法是错误的.
故答案为:×.
【名师点评】此题主要考查长方形面积公式的灵活运用,关键是熟记公式.
28.【考点】三角形的内角和.
【答案】×
【思路分析】等腰三角形两个角之和是130°时,则第三个角是180°﹣130°=50°,这个50°的角可能是顶角,也可能是底角,若为底角,则顶角的度数就是:180°﹣50°×2。据此解答即可。
【解答】解:180°﹣130°=50°
这个50°的角可能是顶角,也可能是底角。
若为底角,则顶角就是:180°﹣50°×2=80°
若为顶角,则底角就是:130°÷2=65°
两角之差为:80﹣50°=30°或65°﹣50°=15度
所以原题干说法错误。
故答案为:×。
【名师点评】本题考查的是等腰三角形的性质,熟知等腰三角形两个底角相等是解答本题的关键。
四.计算题
29.【考点】分数的四则混合运算;小数的加法和减法;小数乘法;小数除法;分数的加法和减法;分数乘法.
【答案】1.06,100,3.6,0.1,0.8,2,27,,,0。
【思路分析】根据分数的四则混合运算,小数的加法和减法的运算方法,小数乘法和除法的运算方法,还有分数加法和减法的运算方法和分数乘法的运算方法,计算解答此题即可。
【解答】解:
0.4+0.66=1.06 5÷0.05=100 6.3﹣2.7=3.6 0.25×0.4=0.1 10.8
32 33=27 3×00
【名师点评】此题主要考查了对分数的四则混合运算,小数的加法和减法的运算方法,小数乘法和除法的运算方法,还有分数加法和减法的运算方法和分数乘法的运算方法的灵活运用。
30.【考点】分数方程求解.
【答案】0.64,1。
【思路分析】先计算出方程左边3x﹣0.5x=2.5x,再根据等式的性质,方程两边同时除以2.5即可得到原方程的解。
根据比例的性质,两外项之积等于两内项之积,把比例式转化成一般方程75x=50×1.5,再根据等式的性质,方程两边同时除以75,即可得到原比例的解。
【解答】解:3x﹣0.5x=1.6
2.5x=1.6
2.5x÷2.5=1.6÷2.5
x=0.64
75x=50×1.5
75x÷75=50×1.5÷75
x=1
【名师点评】解方程的依据是等式的性质。解答过程要注意书写格式:上、下行等号对齐;不能连等。解比例时,先根据比例的性质,两外项之积等于两内项之积,把比例式转化成一般方程,然后再根据解方程的方法解答。
31.【考点】分数的四则混合运算;小数四则混合运算.
【答案】30;12;;3。
【思路分析】(1)运用加法交换律和加法结合律简算;
(2)利用乘法结合律简算;
(3)把除法化成乘法,再利用乘法分配律即可;
(4)先计算乘法,再利用减法的运算性质计算。
【解答】解:12.25+3.6+7.75+6.4
=(12.25+7.75)+(3.6+6.4)
=20+10
=30
12×8×0.125
=12×(8×0.125)
=12×1
=12
=()
4
=4
=4﹣()
=4﹣1
=3
【名师点评】本题主要考查整数、分数、小数的四则混合运算,关键注意运算律的应用。
五.操作题
32.【考点】图形划分.
【答案】
【思路分析】由题意知,要分成形状相同、大小相等的两部分,可运用中心对称的原理,借助画图。
【解答】解:如图:
【名师点评】此题是考查图形的拆分,可利用中心对称的原理经过画图求得答案。
33.【考点】图形的放大与缩小;作轴对称图形;作平移后的图形;作旋转一定角度后的图形.
【答案】(1)(2)(3)(4)
【思路分析】(1)根据轴对称图形的画法,画出图形①的另一半,使它成为一个轴对称图形即可。
(2)根据旋转的方法,O点不动,画出图形②绕O点逆时针旋转90°后的图形即可。
(3)根据平移的方法,画出图形②向右平移3格后的图形。
(4)根据图形放大的方法,按2:1的比将图形②的各边扩大到原来的2倍,形状不变,画出放大后的图形即可。
【解答】解:(1)画出图形①的另一半,使它成为一个轴对称图形。如图:
(2)画出图形②绕O点逆时针旋转90°后的图形。如图:
(3)画出图形②向右平移3格后的图形。如图:
(4)按2:1的比将图形②放大,画出放大后的图形。如图:
【名师点评】本题考查了轴对称图形、平移、旋转以及图形的放大等知识,结合题意分析解答即可。
六.应用题
34.【考点】圆、圆环的面积.
【答案】388.575平方米。
【思路分析】先利用塔蝶直径求出外圆的半径,减去环宽4.5米,就是内圆的半径,再利用圆环的面积公式:S=π(R2﹣r2)即可求出环形露天观光平台的面积。
【解答】解:32÷2=16(米)
16﹣4.5=11.5(米)
3.14×(162﹣11.52)
=3.14×(256﹣132.25)
=3.14×123.75
=388.575(平方米)
答:环形露天观光平台的面积是388.575平方米。
【名师点评】此题的解题关键是掌握圆环的面积的计算方法。
35.【考点】圆柱的侧面积和表面积.
【答案】1142.96平方厘米。
【思路分析】圆柱的高增加了4cm,底面面积还是原来的,只是增加部分的圆柱增加了侧面积。把增加部分展开,看作长方形。长方形的面积就是125.6cm2,宽为4cm。关键是求出长方形的长,用面积除以宽可得长。这个长就是圆柱的底面周长,接下来再求出直径、半径,原来圆柱的表面积就求出来了。还要注意圆柱的底面周长和高相等,据此解答。
【解答】解:125.6÷4=31.4(cm)
31.4×31.4+3.14×(31.4÷3.14÷2)2×2
=985.96+3.14×50
=985.96+157
=1142.96(cm2)
答:原来这个圆柱的表面积是1142.96平方厘米。
【名师点评】本题考查圆柱侧面积和表面积的计算:①圆柱的底面周长和高相等,计算时要注意数据的选取;②高增加了,就增加了表面积,就要研究增加的部分,从求增加部分的底面周长入手。还要注意计算量很大。
36.【考点】比例的应用.
【答案】15米。
【思路分析】同样条件下,物体的高度与它的影子的比是一定的,也就是说,篮球架与其影子的比和教学楼与其影子的比是相等的,据此即可列比例求解。
【解答】解:设教学楼的高度为x米,
则3:4.5=x:22.5
4.5x=3×22.5
4.5x=67.5
x=15
答:教学楼的高度是15米。
【名师点评】解答此题的关键是明白:同样条件下,物体的高度与它的影子的比是一定的.
37.【考点】比的应用.
【答案】588千米。
【思路分析】首先根据路程÷时间=速度,用160除以甲车的时间2小时,求出甲车的速度;然后把两车的速度分别看作4份和3份,用甲车的速度除以4再乘3求出乙车的速度,再用两车的速度之和乘两车的相遇时间即可解答。
【解答】解:160÷2=80(千米/时)
80÷4×3
=60(千米/时)
(80+60)×4.2
=140×4.2
=588(千米)
答:AB两城相距588千米。
【名师点评】此题主要考查了行程问题中速度、时间和路程的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间,解答此题的关键是求出两车的速度之和是多少。
38.【考点】正、反比例应用题;比例尺.
【答案】210千米。
【思路分析】根据比例尺=图上距离:实际距离,比例尺一定,即图上距离与实际距离的比值是一定的,符合正比例的意义,所以图上距离与实际距离成正比例,假设乙、丙两地之间的实际距离是x千米,列出比例,求解即可。
【解答】解:设乙、丙两地之间的实际距离是x厘米,
150千米=15000000厘米
7:x=5:15000000
5x=7×15000000
5x=105000000
x=21000000
21000000厘米=210千米
答:乙、丙两地之间的实际距离是210千米。
【名师点评】解答此题的关键是弄清楚哪两种量成何比例,进而列比例求解。
39.【考点】关于圆柱的应用题.
【答案】(1)1256平方厘米;(2)11304平方厘米;(3)20条。
【思路分析】(1)求鱼缸的占地面积,也就是求圆柱体鱼缸的底座的底面积,根据圆的面积公式S=πr2解答;
(2)鱼缸缸体侧面是透明玻璃制成,所以这个圆柱体的表面是由圆柱侧面组成的,圆柱侧面积公式S=2πrh,将数据代入公式解答即可;
(3)根据圆柱体积公式:圆柱体积=底面积×高;求出水的体积,再换算单位,再除以10升,乘2即可。
【解答】解:(1)40÷2=20(厘米)
3.14×202=1256(平方厘米)
答:这个鱼缸的占地面积是1256平方厘米。
(2)3.14×36×100
=3.14×3600
=11304(平方厘米)
答:制作这个鱼缸需要11304平方厘米的玻璃。
(3)3.14×(36÷2)2×100
=3.14×182×100
=101736(立方厘米)
101736立方厘米=101.736升
101.736÷10×2≈20(条)
答:这个鱼缸大约能养20条5厘米长的鱼。
【名师点评】此题属于圆柱体底面积、侧面积和体积的实际应用,特别是求做这个鱼缸至少要用多少平方分米的玻璃;首先弄清这个鱼缸是由几个面组成的,缺少的是哪个面;然后根据公式解答即可。
21世纪教育网(www.21cnjy.com)
2025年秋六年级数学小升初开学重点校分班摸底押题卷青岛版(六三制)
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一.选择题
1.再添一个小正方形,使它成为一个正方体的展开图,添加的方法共有( )种。
A.3 B.4 C.5
2.把一根4米长的绳子平均分成m段,每段长( )米。
A. B. C. D.
3.数轴上有四个点分别是,﹣1,+2,其中( )更接近0。
A. B. C.﹣1 D.+2
4.三位同学进行小组研究学习,各自表达自己的思路和方法,合理的是( )
A.①②③ B.①② C.②③ D.①③
5.移动公司进行技能大比拼,一件工作,张叔叔单独做8分钟完成,李叔叔单独做10分钟完成,那么下列说法不成立的是( )
A.张叔叔的工作效率和工作时间成正比例
B.李叔叔5天做的工作量,张叔叔只需4天
C.张叔叔用时比李叔叔节省
D.李叔叔的工作效率比张叔叔低20%
6.毕业赠礼物,为了分类摆放提高效率,将4个完全一样的长方体礼物盒子包成一包,扎物盒子的长是10cm,宽是6cm,高是4cm,下面最省包装纸的是( )
A. B. C. D.
7.六年级一周30节课,要反映各学科课时与总课时之间的关系,选择( )比较合适。
A.条形统计图 B.折线统计图 C.扇形统计图
8.一种机器零件,横截面是环形,外直径是8毫米,画在图纸上的长度是4厘米。这张图纸的比例尺是(( )
A.5:1 B.2:1 C.1:2
9.从这四张数字卡片中任选两张,组成不同的两位数。其中3和5的公倍数有( )个。
A.2 B.3 C.4
10.用一张正方形纸卷成一个圆柱形纸筒,这个圆柱体纸筒的底面直径和高的比是( )
A.π:1 B.1:π C.2π:1
二.填空题
11.小强用三根整厘米的小棒拼一个三角形,其中两根小棒的长度分别是5厘米和6厘米,第三根小棒的长度最长是 厘米。
12.一个三角形,它的一个内角度数占内角和的,其余两个角是按剩下度数的2:3来分配的。这个三角形是 三角形。
13.2023年“五一”假期,全国国内旅游出游二亿七千四百万人次,横线上的数写作 人次;实现国内旅游收入148056000000元,省略亿后面的尾数是 亿元。
14.2023年5月10日,第三期和第四期储蓄国债开始发行,其中第三期限期二年,年利率是2.95%,爸爸买了50000元第三期国债,到期时的利息是 元。
15.和都是假分数,的分数单位是 ;如果A是一个合数,那么A表示的数字是 。
16.青岛到杭州全程813.4千米,合 千米 米。一列客车上午7:30从青岛出发,下午3:30到达杭州,这列客车途中共用 小时。
17.实验室有如右图的两个容器,吴老师将2L的药水倒入两个容器中,刚好倒完,两个容器都刚好倒满。已知两个容器的底面积相等,则圆锥形容器的容积是 L。
18.小丽将一张纸对折后,剪出了一个符合轴对称的三角形,将三角形完全展开后,经测量发现其中两条边的长度分别是7厘米和15厘米,如果不考虑小数的情况,另外一条边是 厘米。
19.3吨70千克= 千克 7.5立方米= 升
20.把4千克糖果平均分成8包,每包重 千克,每包占4千克的 。
21.一根底面直径是4分米、高是5分米的圆柱形木材,如果把它截成3段,表面积会增加 平方分米;如果把它沿底面直径切成形状、大小完全相同的两部分,表面积会增加 平方分米。
22.比萨斜塔高54.5米,按1:100的比例尺画出它的平面图,高是 厘米。
三.判断题
23.圆规两脚间的距离是4厘米,画出的圆的周长是12.56厘米。
24.圆柱的体积比与它等底等高的圆锥的体积多. .
25.两条直线相交组成的四个角中如果有一个角是直角,那么其它三个角也是直角. .
26.xyz,那么x、y、z的关系是x>y>z.
27.一个长方形,长增加3米,宽增加4米,它的面积就增加12平方米.
28.一个等腰三角形,两角之和是130°,则两角之差是30°。
四.计算题
29.直接写出得数。
0.4+0.66= 5÷0.05= 6.3﹣2.7= 0.25×0.4= 1
3 33= 3×0
30.解方程或比例。
3x﹣0.5x=1.6
31.脱式计算(能简算的要简算)
12.25+3.6+7.75+6.4 12×8×0.125
4
五.操作题
32.请用4种方法把图中的正方形分成形状相同、大小相等的四块。
33.动手操作。
(1)画出图形①的另一半,使它成为一个轴对称图形。
(2)画出图形②绕O点逆时针旋转90°后的图形。
(3)画出图形②向右平移3格后的图形。
(4)按2:1的比将图形②放大,画出放大后的图形。
六.应用题
34.青岛电视塔的塔蝶直径为32米,塔蝶之上的环形露天观光平台的宽度是4.5米。环形露天观光平台的面积是多少?
35.一个圆柱的底面周长和高相等,如果高增加4cm,表面积就增加125.6cm2,原来这个圆柱的表面积是多少平方厘米?
36.测量小组测量教学楼的影子长是22.5米,同时量得附近一个3米高的篮球架的影子长是4.5米,教学楼高多少米?(用比例知识解答)
37.甲乙两车分别从AB两城相对开出。甲车2小时行驶了160千米,甲乙车的速度比是4:3,两车行驶了4.2小时相遇。AB两城相距多少千米?
38.甲、乙两地相距150千米,在一幅地图上量得甲、乙两地之间的距离是5厘米,同时在这幅地图上量得乙、丙两地之间的距离是7厘米,乙、丙两地之间的实际距离是多少千米?(用比例解)
39.可乐家新买一圆柱形鱼缸,测得缸体直径36厘米等数据如图所示:
(1)这个鱼缸的占地面积是多少平方厘米?
(2)鱼缸缸体侧面是透明玻璃制成,这个圆柱形鱼缸需要多少玻璃?
(3)水族界有个比较公认的算法:一升水大约能养1厘米长的一条鱼,比如10升水就大约能养10厘米长的一条鱼或者养1厘米长的10条鱼。那么这个鱼缸大约能养多少条5厘米长的鱼?
参考答案及试题解析
一.选择题
1.【考点】正方体的展开图.
【答案】B
【思路分析】根据正方体展开图的11种特征,再下层的任一个正方形的正面再画一个相同的正方形,即可使之成为一个正方体展开图的“1﹣4﹣1”型。
【解答】解:如图:
再添一个小正方形,使它成为一个正方体的展开图,添加的方法共有4种。
故选:B。
【名师点评】此题是考查正方体展开图的认识。正方体展开图分四种类型,11种情况,要掌握每种情况的特征。
2.【考点】分数除法应用题.
【答案】D
【思路分析】求每段长多少米,是把4米平均分成m份,所以用这根绳子的长度除以平均分成的段数就是每段的长度。
【解答】解:4÷m(米)
答:每段长米。
故选:D。
【名师点评】解决此题关键是弄清求的是“分率”还是“具体的数量”,求分率:平均分的是单位“1”;求具体的数量:平均分的是具体的数量,要注意:分率不能带单位名称,而具体的数量要带单位名称。
3.【考点】数轴的认识;正、负数大小的比较.
【答案】B
【思路分析】根据题意,与0相差,与0相差,﹣1与0相差1,+2与0相差2,据此比较解答即可。
【解答】解:与0相差,与0相差,﹣1与0相差1,+2与0相差2,
因为1<2,所以更接近0。
故选:B。
【名师点评】本题考查了数轴知识,结合比较大小的方法解答即可。
4.【考点】数学常识.
【答案】D
【思路分析】根据题意,①中竖式计算12÷5时,余下的2表示2个一,后面添上0后,表示20个十分之一,据此分析即可;
②中22×9÷2,据此分析即可;
③中(1)×(2)=(1×2)×(),据此解答即可。
【解答】解:①中竖式计算12÷5时,余下的2表示2个一,后面添上0后,表示20个十分之一,所以原说法正确;
②中22×9÷2,所以原说法错误;
③中(1)×(2)=(1×2)×(),所以原说法正确。
所以三位同学进行小组研究学习,各自表达自己的思路和方法,合理的是①③。
故选:D。
【名师点评】本题考查了除法竖式计算以及分数乘除法计算的算理知识,结合题意分析解答即可。
5.【考点】辨识成正比例的量与成反比例的量;百分数的实际应用;简单的工程问题.
【答案】A
【思路分析】先根据“工作量=工作效率×工作时间”,直接判断选项A的说法是否正确;再将工作量设为1,由题意可知,张叔叔单独做每分钟完成,李叔叔单独做每分钟完成。据此计算后判断B、C、D的说法是否正确。
【解答】解:选项A,工作量=工作效率×工作时间,这件工作的工作量一定,张叔叔的工作效率和工作时间成反比例。原题说法错误;
选项B,5
=4(天)
答:李叔叔5天做的工作量,张叔叔只需4天。
原题说法正确;
选项C,(10﹣8)÷10
=2÷10
答:张叔叔用时比李叔叔节省。
原题说法正确;
选项D,()
=0.2
=20%
答:李叔叔的工作效率比张叔叔低20%。
原题说法正确。
故选:A。
【名师点评】解答本题需明确成正比例和成反比例的判定方法,熟练掌握工作量、工作时间和工作效率之间的关系,熟记求一个数比另一个数多(少)几分之几或百分之几的计算方法。
6.【考点】长方体和正方体的表面积.
【答案】C
【思路分析】根据长方体表面积的意义可知,要想最节省包装纸,也就是把4个完全一样的长方体礼品盒的最大面重合摞起来进行包装,据此解答即可。
【解答】解:要想最节省包装纸,也就是把4个完全一样的长方体礼品盒的最大面重合摞起来进行包装。
故选:C。
【名师点评】此题考查的目的是理解掌握长方体表面积的意义及应用。
7.【考点】统计图的选择.
【答案】C
【思路分析】首先要清楚每一种统计图的优点:条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系;由此根据情况选择即可。
【解答】解:六年级一周30节课,要反映各学科课时与总课时之间的关系,选择扇形比较合适。
故选:C。
【名师点评】解答此题要熟练掌握统计图的特点,根据实际情况灵活选择。
8.【考点】比例尺.
【答案】A
【思路分析】图上距离:实际距离=比例尺,据此代入数据解答即可。
【解答】解:4厘米:8毫米
=40毫米:8毫米
=40:8
=5:1
答:这张图纸的比例尺是5:1。
故选:A。
【名师点评】熟练掌握比例尺的意义是解题的关键。
9.【考点】公倍数和最小公倍数.
【答案】A
【思路分析】根据题意,组成的两位数是:10、30、50、13、31、15、51、35、53,这些数中只有30和15是3和5的公倍数。
【解答】解:从0、1、3、5这四张数字卡片中任选两张,组成不同的两位数。其中3和5的公倍数有2个,分别是15和30。
故答案为:A。
【名师点评】此题考查了数的组成和3和5的公倍数,要求学生掌握。
10.【考点】比的意义;圆柱的展开图.
【答案】B
【思路分析】用一张正方形纸围成一个圆柱形纸筒,圆柱的底面周长等于正方形的边长,圆柱的高等于正方形的边长,据此判断选择即可。
【解答】解:设这个正方形的边长为a,则圆柱的底面周长等于a,圆柱的高等于a,则这个圆柱体纸筒的底面直径和高的比是
(a÷π):a=1:π
故选:B。
【名师点评】解答本题的关键是明确:圆柱的底面周长等于正方形的边长,圆柱的高等于正方形的边长。
二.填空题
11.【考点】三角形边的关系;三角形的特性.
【答案】10。
【思路分析】任意三角形的两边之和必须大于第三边,任意两边的差必须小于第三边,据此解答。
【解答】解:5+6=11(厘米)
11﹣1=10(厘米)
答:第三根小棒的长度最长是10厘米。
故答案为:10。
【名师点评】本题考查了三角形的三边关系的应用。
12.【考点】按比例分配应用题;三角形的分类.
【答案】直角。
【思路分析】把内角和180度看作单位“1“,用180°乘,求出它的一个内角度数,再用180°减去它的一个内角度数,求出其余两个角的度数和,又知道其余两个角是按剩下度数的2:3来分配的。再用其余两个角的度数和除以(2+3),求出一份是多少度,再分别乘2、3求出其余两个角各是多少度,再判断三角形的类型。
【解答】解:180°30°
(180°﹣30°)×(2+3)
=150°÷5
=30°
30°×2=60°
30°×3=90°
有一个角是直角90°,所以这个三角形是等腰直角三角形。
答:这个三角形是直角三角形。
故答案为:直角。
【名师点评】本题考查了三角形的类型、内角和和按比例分配问题。
13.【考点】亿以上数的读写;亿以上数的改写与近似.
【答案】见试题解答内容
【思路分析】根据整数的写法,从高位到低位,一级一级地写,哪一个数位上一个计数单位也没有,就在那个数位上写0,即可写出此数;省略“亿”后面的尾数就是四舍五入到亿位,就是把亿位后的千万位上的数进行四舍五入,再在数的后面写上“亿”字。
【解答】解:二亿七千四百万写作:274000000;148056000000≈1481亿。
故答案为:274000000,1481。
【名师点评】本题主要考查整数的写法和求近似数,分级写或借助数位表写数能较好的避免写错数的情况,求近似数时要注意带计数单位。
14.【考点】存款利息与纳税相关问题.
【答案】2950元。
【思路分析】取出的钱数=买国债用的钱数×年利率×年数,结合已知数据,列式计算,求出取出的钱数即可。
【解答】解:50000×2.95%×2
=100000×0.0295
=2950(元)
答:到期时的利息是2950元。
故答案为:2950元。
【名师点评】本题是一道关于百分数应用的题目,解答本题的关键是掌握取出的钱数的计算方法。
15.【考点】分数的意义和读写;用字母表示数.
【答案】,6。
【思路分析】分数单位是把单位“1”平均分成若干份,表示其中的一份的数;假分数就是分子大于分母(或等于分母)的数;合数是在大于1的整数中,除了能被1和本身整除外,还能被其他数(0除外)整除的数。
【解答】解:和都是假分数,的分数单位是,如果A是一个合数,那么A表示的数字是6。
故答案为:,6。
【名师点评】此题考查了假分数、分数单位以及合数的知识,要求学生掌握。
16.【考点】日期和时间的推算.
【答案】见试题解答内容
【思路分析】1千米=1000米,根据低级单位换算成高级单位用除法计算,高级单位换算成低级单位用乘法计算完成填空。
运用结束时刻﹣开始时刻=经过的时间。
【解答】解:813.4千米,合813千米400米。
下午3:30=15时30分
15时30分﹣7时30分=8小时
故答案为:813,400;8。
【名师点评】本题考查时间的推算及长度单位之间的换算,要牢记这些单位之间的进率和换算规则。
17.【考点】圆锥的体积.
【答案】0.5。
【思路分析】因为等底等高的圆柱的体积是圆锥体积的3倍,所以等底等高的圆柱与圆锥的体积和相当于圆锥体积的(3+1)倍,根据已知一个数的几倍是多少,求这个数,用除法解答。
【解答】解:2÷(3+1)
=2÷4
=0.5(升)
答:圆锥形容器的容积是0.5升。
故答案为:0.5。
【名师点评】此题考查的目的是理解掌握等底等高的圆柱与圆锥体积之间的关系及应用。
18.【考点】简单图形的折叠问题.
【答案】15。
【思路分析】根据剪成的三角形符合轴对称的三角形,可知这是一个等腰三角形,在三角形中。两边之和要大于第三边,如果7厘米是腰长,7+7<15,所以不符合三角形边的规律,据此可知另一条腰长是15厘米。据此解答即可。
【解答】解:7+7<15
15+15>7
所以另外一条边是15厘米。
故答案为:15。
【名师点评】本题考查三角形边的关系。
19.【考点】体积、容积进率及单位换算;质量的单位换算.
【答案】3070,7500。
【思路分析】把3吨乘进率1000化成3000千克再加70千克。
高级单位立方米化低级单位升乘进率1000。
【解答】解:3吨70千克=3070千克
7.5立方米=7500升
故答案为:3070,7500。
【名师点评】此题是考查质量的单位换算、体积(容积)的单位换算。单位换算首先要弄清是由高级单位化低级单位还是由低级单位化高级单位,其次记住单位间的进率。
20.【考点】分数的意义和读写.
【答案】。
【思路分析】根据题意,求每包重多少千克,利用总质量除以包数即可,求每包占总质量的几分之几,利用1除以8即可。
【解答】解:4(千克)
1
答:每包重千克,每包占4千克的。
故答案为:。
【名师点评】本题考查了分数的意义及应用。
21.【考点】圆柱的侧面积、表面积和体积;简单的立方体切拼问题.
【答案】50.24,40。
【思路分析】根据题意可知,把这根圆柱形木料横截成3段,表面积增加4个底面的面积;如果把它沿底面直径切成形状、大小完全相同的两部分,表面积会增加两个切面的面积,每个切面的长等于圆柱的高,每个切面的宽等于圆柱的底面直径,根据圆的面积公式:S=πr2,长方形的面积公式:S=ab,把数据代入公式解答。
【解答】解:3.14×(4÷2)2×4
=3.14×4×4
=12.56×4
=50.24(平方分米)
5×4×2
=20×2
=40(平方分米)
答:如果把它截成3段,表面积会增加50.24平方分米,如果把它沿底面直径切成形状、大小完全相同的两部分,表面积会增加40平方分米。
故答案为:50.24,40。
【名师点评】此题考查的目的是理解掌握圆柱表面积的意义及应用,圆的面积公式、长方形的面积公式及应用。
22.【考点】图上距离与实际距离的换算(比例尺的应用).
【答案】54.5。
【思路分析】图上距离=实际距离×比例尺,据此代入数据解答即可。
【解答】解:54.5米=5450厘米
545054.5(厘米)
答:高是54.5厘米。
故答案为:54.5。
【名师点评】熟练掌握比例尺、图上距离、实际距离三者间的关系是解题的关键。
三.判断题
23.【考点】圆、圆环的周长.
【答案】×
【思路分析】用圆规画圆时,圆规两脚间的距离是4厘米,画出圆的半径是4厘米,根据圆的周长公式:C=2πr,把数据代入公式解答。
【解答】解:3.14×4×2
=3.14×8
=25.12(厘米)
答:画出的圆的周长是25.12厘米。
所以原题说法是错误的。
故答案为:×。
【名师点评】此题主要考查圆周长公式的灵活运用,关键是熟记公式。
24.【考点】圆锥的体积.
【答案】见试题解答内容
【思路分析】因为一个圆柱的体积是与它等底等高的圆锥体积的3倍,所以圆柱体积比与它等底等高的圆锥体积大2倍.
【解答】解:因为一个圆柱的体积是与它等底等高的圆锥体积的3倍,
所以圆柱体积比与它等底等高的圆锥体积大:(3﹣1)÷1=2倍.
故答案为:×.
【名师点评】此题是考查圆柱、圆锥的关系,要注意圆柱和圆锥在等底等高的条件下体积有3倍或的关系.
25.【考点】垂直与平行的特征及性质.
【答案】见试题解答内容
【思路分析】两条直线相交,有两种情况,垂直或不垂直,如果其中一个角是90°,那么其它各个角都是90°,这两条直线就相互垂直.
【解答】解:由垂直的含义可知:两条直线相交组成的四个角中如果有一个角是直角,那么其它三个角也是直角,
所以原题说法正确;
故答案为:√.
【名师点评】此题考查了垂直的含义,注意对一些基础概念和性质的理解.
26.【考点】分数的大小比较.
【答案】×
【思路分析】已知xyz,由它们的和相等,一个加数大另一个加数就小,比较加数的大小,即可得出另一个加数的大小,再判断即可.
【解答】解:
,
所以
所以x<y<z;
故答案为:×.
【名师点评】此题考查了两个加数与和之间的关系.
27.【考点】长方形、正方形的面积.
【答案】×
【思路分析】根据长方形的面积公式:S=ab,长方形长和宽增加后,又形成了三个长方形,三个长方形的面积和即为增加的面积,据此可列式推算判断即可.
【解答】解:如图:
则增加的面积为:4a+3b+4×3=4a+3b+12
因a、b不能为0,所以4a+3b+12>12
所以一个长方形,长增加3米,宽增加4米,它的面积就增加12平方米.这种说法是错误的.
故答案为:×.
【名师点评】此题主要考查长方形面积公式的灵活运用,关键是熟记公式.
28.【考点】三角形的内角和.
【答案】×
【思路分析】等腰三角形两个角之和是130°时,则第三个角是180°﹣130°=50°,这个50°的角可能是顶角,也可能是底角,若为底角,则顶角的度数就是:180°﹣50°×2。据此解答即可。
【解答】解:180°﹣130°=50°
这个50°的角可能是顶角,也可能是底角。
若为底角,则顶角就是:180°﹣50°×2=80°
若为顶角,则底角就是:130°÷2=65°
两角之差为:80﹣50°=30°或65°﹣50°=15度
所以原题干说法错误。
故答案为:×。
【名师点评】本题考查的是等腰三角形的性质,熟知等腰三角形两个底角相等是解答本题的关键。
四.计算题
29.【考点】分数的四则混合运算;小数的加法和减法;小数乘法;小数除法;分数的加法和减法;分数乘法.
【答案】1.06,100,3.6,0.1,0.8,2,27,,,0。
【思路分析】根据分数的四则混合运算,小数的加法和减法的运算方法,小数乘法和除法的运算方法,还有分数加法和减法的运算方法和分数乘法的运算方法,计算解答此题即可。
【解答】解:
0.4+0.66=1.06 5÷0.05=100 6.3﹣2.7=3.6 0.25×0.4=0.1 10.8
32 33=27 3×00
【名师点评】此题主要考查了对分数的四则混合运算,小数的加法和减法的运算方法,小数乘法和除法的运算方法,还有分数加法和减法的运算方法和分数乘法的运算方法的灵活运用。
30.【考点】分数方程求解.
【答案】0.64,1。
【思路分析】先计算出方程左边3x﹣0.5x=2.5x,再根据等式的性质,方程两边同时除以2.5即可得到原方程的解。
根据比例的性质,两外项之积等于两内项之积,把比例式转化成一般方程75x=50×1.5,再根据等式的性质,方程两边同时除以75,即可得到原比例的解。
【解答】解:3x﹣0.5x=1.6
2.5x=1.6
2.5x÷2.5=1.6÷2.5
x=0.64
75x=50×1.5
75x÷75=50×1.5÷75
x=1
【名师点评】解方程的依据是等式的性质。解答过程要注意书写格式:上、下行等号对齐;不能连等。解比例时,先根据比例的性质,两外项之积等于两内项之积,把比例式转化成一般方程,然后再根据解方程的方法解答。
31.【考点】分数的四则混合运算;小数四则混合运算.
【答案】30;12;;3。
【思路分析】(1)运用加法交换律和加法结合律简算;
(2)利用乘法结合律简算;
(3)把除法化成乘法,再利用乘法分配律即可;
(4)先计算乘法,再利用减法的运算性质计算。
【解答】解:12.25+3.6+7.75+6.4
=(12.25+7.75)+(3.6+6.4)
=20+10
=30
12×8×0.125
=12×(8×0.125)
=12×1
=12
=()
4
=4
=4﹣()
=4﹣1
=3
【名师点评】本题主要考查整数、分数、小数的四则混合运算,关键注意运算律的应用。
五.操作题
32.【考点】图形划分.
【答案】
【思路分析】由题意知,要分成形状相同、大小相等的两部分,可运用中心对称的原理,借助画图。
【解答】解:如图:
【名师点评】此题是考查图形的拆分,可利用中心对称的原理经过画图求得答案。
33.【考点】图形的放大与缩小;作轴对称图形;作平移后的图形;作旋转一定角度后的图形.
【答案】(1)(2)(3)(4)
【思路分析】(1)根据轴对称图形的画法,画出图形①的另一半,使它成为一个轴对称图形即可。
(2)根据旋转的方法,O点不动,画出图形②绕O点逆时针旋转90°后的图形即可。
(3)根据平移的方法,画出图形②向右平移3格后的图形。
(4)根据图形放大的方法,按2:1的比将图形②的各边扩大到原来的2倍,形状不变,画出放大后的图形即可。
【解答】解:(1)画出图形①的另一半,使它成为一个轴对称图形。如图:
(2)画出图形②绕O点逆时针旋转90°后的图形。如图:
(3)画出图形②向右平移3格后的图形。如图:
(4)按2:1的比将图形②放大,画出放大后的图形。如图:
【名师点评】本题考查了轴对称图形、平移、旋转以及图形的放大等知识,结合题意分析解答即可。
六.应用题
34.【考点】圆、圆环的面积.
【答案】388.575平方米。
【思路分析】先利用塔蝶直径求出外圆的半径,减去环宽4.5米,就是内圆的半径,再利用圆环的面积公式:S=π(R2﹣r2)即可求出环形露天观光平台的面积。
【解答】解:32÷2=16(米)
16﹣4.5=11.5(米)
3.14×(162﹣11.52)
=3.14×(256﹣132.25)
=3.14×123.75
=388.575(平方米)
答:环形露天观光平台的面积是388.575平方米。
【名师点评】此题的解题关键是掌握圆环的面积的计算方法。
35.【考点】圆柱的侧面积和表面积.
【答案】1142.96平方厘米。
【思路分析】圆柱的高增加了4cm,底面面积还是原来的,只是增加部分的圆柱增加了侧面积。把增加部分展开,看作长方形。长方形的面积就是125.6cm2,宽为4cm。关键是求出长方形的长,用面积除以宽可得长。这个长就是圆柱的底面周长,接下来再求出直径、半径,原来圆柱的表面积就求出来了。还要注意圆柱的底面周长和高相等,据此解答。
【解答】解:125.6÷4=31.4(cm)
31.4×31.4+3.14×(31.4÷3.14÷2)2×2
=985.96+3.14×50
=985.96+157
=1142.96(cm2)
答:原来这个圆柱的表面积是1142.96平方厘米。
【名师点评】本题考查圆柱侧面积和表面积的计算:①圆柱的底面周长和高相等,计算时要注意数据的选取;②高增加了,就增加了表面积,就要研究增加的部分,从求增加部分的底面周长入手。还要注意计算量很大。
36.【考点】比例的应用.
【答案】15米。
【思路分析】同样条件下,物体的高度与它的影子的比是一定的,也就是说,篮球架与其影子的比和教学楼与其影子的比是相等的,据此即可列比例求解。
【解答】解:设教学楼的高度为x米,
则3:4.5=x:22.5
4.5x=3×22.5
4.5x=67.5
x=15
答:教学楼的高度是15米。
【名师点评】解答此题的关键是明白:同样条件下,物体的高度与它的影子的比是一定的.
37.【考点】比的应用.
【答案】588千米。
【思路分析】首先根据路程÷时间=速度,用160除以甲车的时间2小时,求出甲车的速度;然后把两车的速度分别看作4份和3份,用甲车的速度除以4再乘3求出乙车的速度,再用两车的速度之和乘两车的相遇时间即可解答。
【解答】解:160÷2=80(千米/时)
80÷4×3
=60(千米/时)
(80+60)×4.2
=140×4.2
=588(千米)
答:AB两城相距588千米。
【名师点评】此题主要考查了行程问题中速度、时间和路程的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间,解答此题的关键是求出两车的速度之和是多少。
38.【考点】正、反比例应用题;比例尺.
【答案】210千米。
【思路分析】根据比例尺=图上距离:实际距离,比例尺一定,即图上距离与实际距离的比值是一定的,符合正比例的意义,所以图上距离与实际距离成正比例,假设乙、丙两地之间的实际距离是x千米,列出比例,求解即可。
【解答】解:设乙、丙两地之间的实际距离是x厘米,
150千米=15000000厘米
7:x=5:15000000
5x=7×15000000
5x=105000000
x=21000000
21000000厘米=210千米
答:乙、丙两地之间的实际距离是210千米。
【名师点评】解答此题的关键是弄清楚哪两种量成何比例,进而列比例求解。
39.【考点】关于圆柱的应用题.
【答案】(1)1256平方厘米;(2)11304平方厘米;(3)20条。
【思路分析】(1)求鱼缸的占地面积,也就是求圆柱体鱼缸的底座的底面积,根据圆的面积公式S=πr2解答;
(2)鱼缸缸体侧面是透明玻璃制成,所以这个圆柱体的表面是由圆柱侧面组成的,圆柱侧面积公式S=2πrh,将数据代入公式解答即可;
(3)根据圆柱体积公式:圆柱体积=底面积×高;求出水的体积,再换算单位,再除以10升,乘2即可。
【解答】解:(1)40÷2=20(厘米)
3.14×202=1256(平方厘米)
答:这个鱼缸的占地面积是1256平方厘米。
(2)3.14×36×100
=3.14×3600
=11304(平方厘米)
答:制作这个鱼缸需要11304平方厘米的玻璃。
(3)3.14×(36÷2)2×100
=3.14×182×100
=101736(立方厘米)
101736立方厘米=101.736升
101.736÷10×2≈20(条)
答:这个鱼缸大约能养20条5厘米长的鱼。
【名师点评】此题属于圆柱体底面积、侧面积和体积的实际应用,特别是求做这个鱼缸至少要用多少平方分米的玻璃;首先弄清这个鱼缸是由几个面组成的,缺少的是哪个面;然后根据公式解答即可。
21世纪教育网(www.21cnjy.com)
同课章节目录
