2024-2025学年河北省邢台市襄都区八年级(下)段考数学试卷(一)(含答案)
文档属性
| 名称 | 2024-2025学年河北省邢台市襄都区八年级(下)段考数学试卷(一)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 107.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 11:51:13 | ||
图片预览



文档简介
2024-2025学年河北省邢台市襄都区八年级(下)段考数学试卷(一)
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.根据下列表述,能确定位置的是( )
A. 红星东街 B. 东经106°,北纬32°
C. 太平洋影城3号厅2排 D. 负二层停车场
2.如下表,若田径场的位置可以表示为A1区,则办公楼的位置可以表示为( )
序号 1 2 3 4
A 田径场 喷泉 教学楼 实验楼
B 篮球场 办公楼 食堂 宿舍楼
A. B2区 B. B3区 C. A2区 D. A3区
3.每年的6月6日是全国爱眼日,2023年爱眼日的主题是“关注普遍的眼睛健康”.某中学七年级数学活动兴趣小组为了解该校2000名学生的视力情况,制定了如下调查方案,最合理的方案是( )
A. 按学籍号随机抽取200名学生进行调查 B. 按学籍号随机抽取5名学生进行调查
C. 抽取本校九年级全体学生进行调查 D. 抽取八年级100名女生进行调查
4.若点A(-4,3)与点B关于原点对称,则点B的纵坐标为( )
A. 4 B. -4 C. 3 D. -3
5.某学习小组将要进行一次统计活动,下面是四位同学分别设计的活动序号,其中正确的是( )
A. 实际问题→收集数据→表示数据→整理数据→统计分析合理决策
B. 实际问题→表示数据→收集数据→整理数据→统计分析合理决策
C. 实际问题→收集数据→整理数据→表示数据→统计分析合理决策
D. 实际问题→整理数据→收集数据→表示数据→统计分析合理决策
6.某校为了了解学生在校午餐所需的时间,抽查了20名同学在校午餐所需的时间,获得如下数据(单位:分):10,12,15,10,16,18,19,18,20,34,22,25,20,18,18,20,15,16,21,16.若将这些数据分为5组,则组距是( )
A. 4分 B. 5分 C. 6分 D. 7分
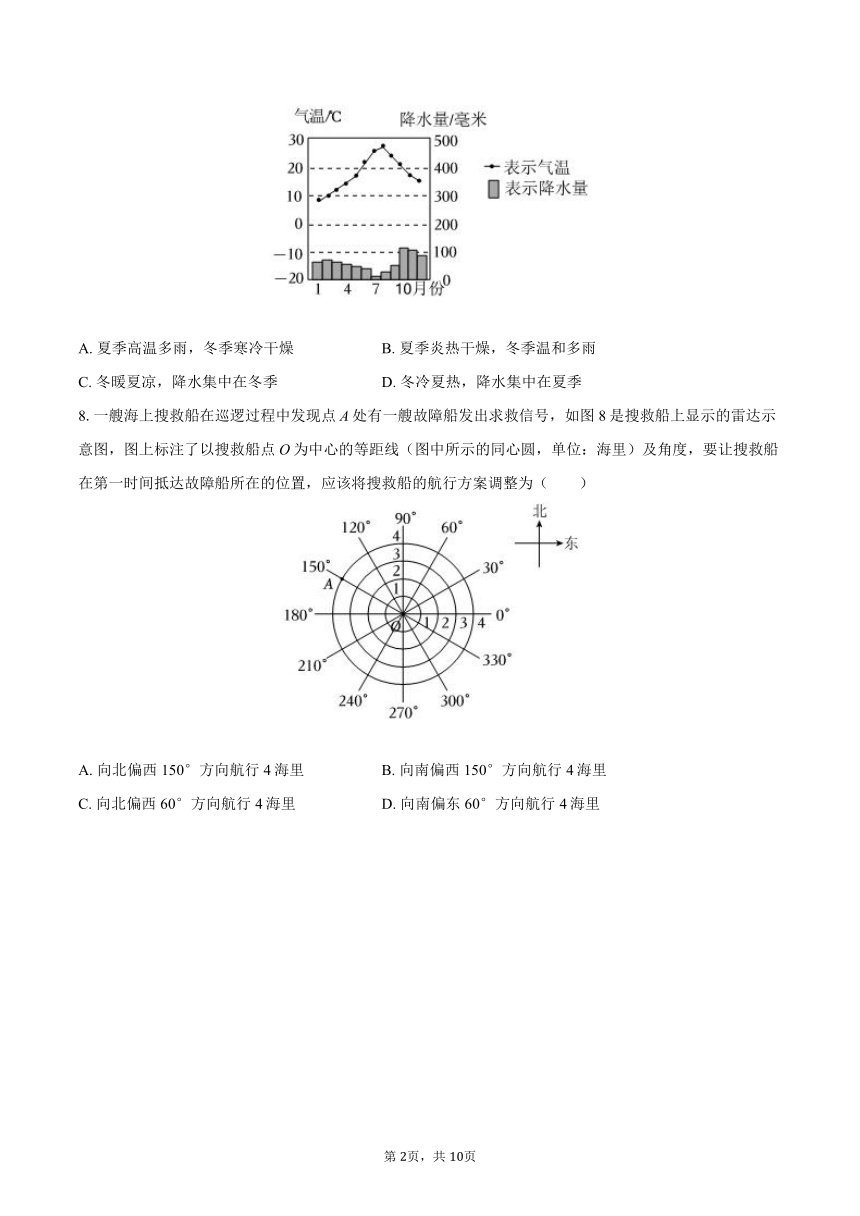
7.如图所示为某地的气候资料,根据图中信息推断,下列说法正确的是( )
A. 夏季高温多雨,冬季寒冷干燥 B. 夏季炎热干燥,冬季温和多雨
C. 冬暖夏凉,降水集中在冬季 D. 冬冷夏热,降水集中在夏季
8.一艘海上搜救船在巡逻过程中发现点A处有一艘故障船发出求救信号,如图8是搜救船上显示的雷达示意图,图上标注了以搜救船点O为中心的等距线(图中所示的同心圆,单位:海里)及角度,要让搜救船在第一时间抵达故障船所在的位置,应该将搜救船的航行方案调整为( )
A. 向北偏西150°方向航行4海里 B. 向南偏西150°方向航行4海里
C. 向北偏西60°方向航行4海里 D. 向南偏东60°方向航行4海里
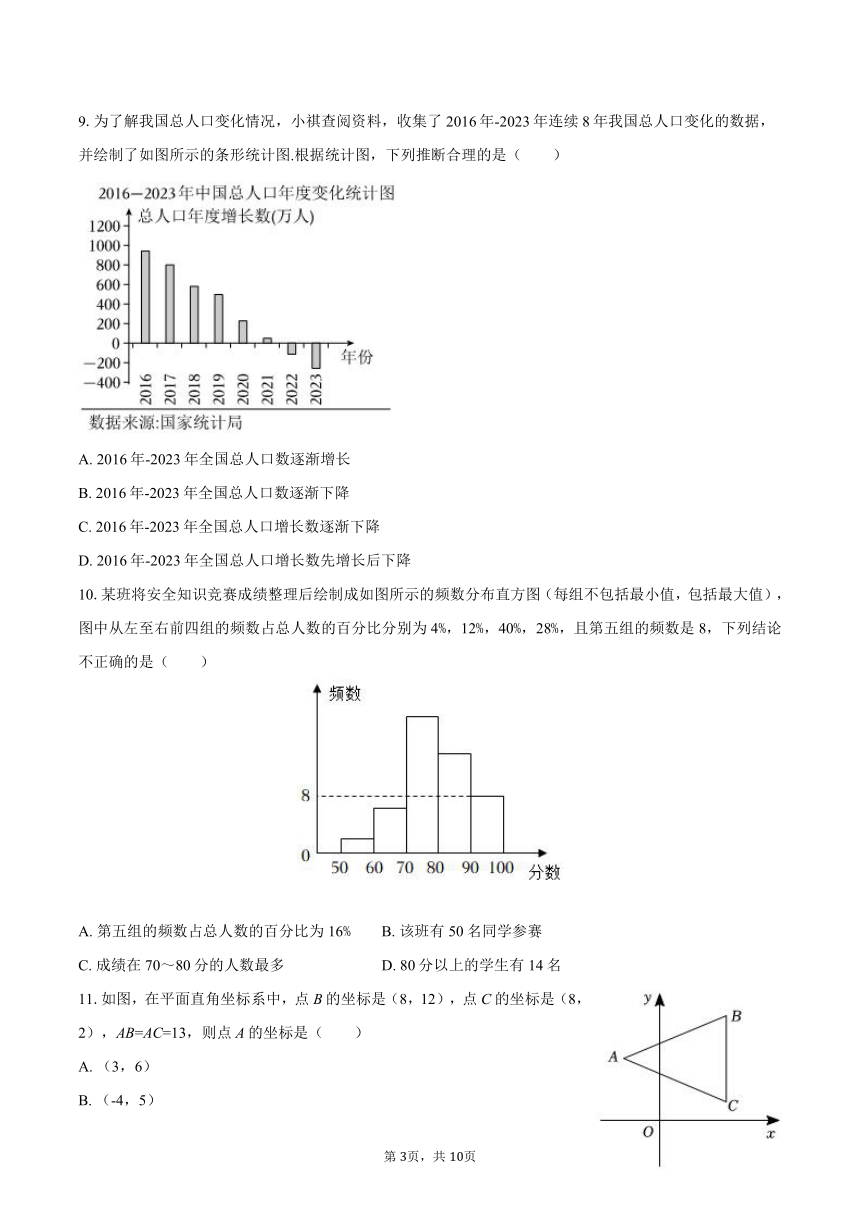
9.为了解我国总人口变化情况,小祺查阅资料,收集了2016年-2023年连续8年我国总人口变化的数据,并绘制了如图所示的条形统计图.根据统计图,下列推断合理的是( )
A. 2016年-2023年全国总人口数逐渐增长
B. 2016年-2023年全国总人口数逐渐下降
C. 2016年-2023年全国总人口增长数逐渐下降
D. 2016年-2023年全国总人口增长数先增长后下降
10.某班将安全知识竞赛成绩整理后绘制成如图所示的频数分布直方图(每组不包括最小值,包括最大值),图中从左至右前四组的频数占总人数的百分比分别为4%,12%,40%,28%,且第五组的频数是8,下列结论不正确的是( )
A. 第五组的频数占总人数的百分比为16% B. 该班有50名同学参赛
C. 成绩在70~80分的人数最多 D. 80分以上的学生有14名
11.如图,在平面直角坐标系中,点B的坐标是(8,12),点C的坐标是(8,2),AB=AC=13,则点A的坐标是( )
A. (3,6)
B. (-4,5)
C. (-4,6)
D. (-4,7)
12.平面直角坐标系中,我们把横、纵坐标都是整数,且横、纵坐标之和大于0的点称为“和点”.将某“和点”平移,每次平移的方向取决于该点横、纵坐标之和除以4所得的余数(当余数为0时,向右平移;当余数为1时,向上平移;当余数为2时,向左平移;余数为3时,向下平移),每次平移1个单位长度.“和点”P(2,1)按上述规则连续平移3次后,到达点P3(1,1),其平移过程如下:.若“和点”R按上述规则连续平移10次后,到达点R10(7,2),则点R的坐标为( )
A. (12,-3) B. (-9,3) C. (9,-3) D. (-12,3)
二、填空题:本题共4小题,每小题3分,共12分。
13.某校为了解本校1200名学生的周末做家务时间,从中抽查了200名学生的周末做家务时间进行统计,则样本容量为______.
14.已知点P(-4a,2+b)在第三象限,则点Q(a,b)在第______象限.
15.如图是一家灯泡生产厂商的广告图,从统计学角度判断广告语不合适,理由是______.
16.已知A(6,-3),B(-2,4),C(2,-1),,则=______.
三、解答题:本题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题7分)
春节过了,你想了解你班里的同学参加社会实践活动情况,你打算实施调查之后再加以总结,那么:
(1)你调查的问题是什么?
(2)你调查的对象是什么?
18.(本小题8分)
小雨同学为调查一个月内全校1000名学生的借书情况,在校园里对学生进行调查,并绘制了如下表格:
借书次数 0 1 2 3 4及4以上
学生人数 45 33 15 5 2
(1)小雨同学采用的是什么调查方式?
(2)总体、个体、样本各是什么?
19.(本小题8分)
你玩过五子棋吗?它的比赛规则是:两人各拥有一种颜色的棋子,每人每次在正方形网格的格点处下一子,两人轮流下,只要连续的同色5个棋子先成一条直线就算胜.如图,是两人玩的一盘棋,若棋盘上白棋①的坐标为(-3,-2),黑棋②的坐标为(-1,0).
(1)请你根据题意,画出相应的平面直角坐标系;
(2)现轮到黑棋下,要使黑棋在这一步要赢,请写出这一步黑棋的坐标.
20.(本小题8分)
在平面直角坐标系中,已知点M(m,2m+3).
(1)若点M在x轴上,则m的值为______;
(2)若点M到x轴、y轴的距离相等,求m的值.
21.(本小题9分)
某校开展了学生的兴趣活动问卷调查,问卷中涉及的兴趣活动有书法、围棋、剪纸、绘画、阅读共五项,参与问卷调查的学生每人必选且只选一项.抽取其中一部分问卷进行整理,分别得到如下统计表和统计图.
学生的兴趣活动统计表
兴趣活动 书法 围棋 剪纸 绘画 阅读
人数 a 30 b 20 40
请根据统计表和统计图提供的信息,解答下列问题:
(1)a= ______,b= ______;
(2)在扇形统计图中,求“阅读”兴趣活动所对应扇形的圆心角的度数;
(3)已知该校共有1200名学生,为使这些学生能够参加自己所喜爱的兴趣活动,该校计划设立5个用于开展不同兴趣活动的专用场地,每个专用场地最多可容纳300人.试问这样的设立计划能否满足所有有意向参加兴趣活动的学生同时进行学习的需求,请说明理由.
22.(本小题9分)
为了解八年级学生每天完成课外作业时间的情况、从全区八年级学生中随机抽取了部分学生每天完成课外作业的时间进行调查,并将调查结果绘制成如下图表:
时间x(小时) 频数y(人数) 频率
0≤x≤0.5 8 0.2
0.5<x≤1 c 0.3
1<x≤1.5 12 0.3
1.5<x≤2 6 b
2<x≤2.5 2 0.05
合计 a 1
(1)a= ______,b= ______,c= ______;
(2)补全频数分布直方图;
(3)根据规定,学生每天完成课外作业的时间不超过1.5小时,那么全区4800名八年级学生中每天完成课外作业时间超过规定的学生约有多少人?
23.(本小题11分)
在数学研究课上,研究小组研究了平面直角坐标系中的特殊线段的长度:在平面直角坐标系中有不重合的两点M(x1,y1)和点N(x2,y2),若x1=x2,则MN∥y轴,且线段MN的长度为|y1-y2|,若y1=y2,则MN∥x轴,且线段MN的长度为|x1-x2|.
【实践操作】
(1)若点M(-1,1),N(2,1),则MN∥x轴,MN的长度为______;若点M(1,0),且MN∥y轴,且MN=2,则点N的坐标为______.
【拓展应用】
(2)如图,在平面直角坐标系中,A(-4,0),B(0,2),C(0,-3).
①如图1,△ABC的面积为______;
②如图2,点D在线段AB上,将点D沿x轴正方向向右平移3个单位长度至E点,若△ACE的面积等于14,求点D坐标.
24.(本小题12分)
阅读理解:
在平面直角坐标系中,经过点M(0,m)且平行于x轴的直线记作直线y=m.
给出如下知识:
①把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线成轴对称,这条直线叫做对称轴,折叠后重合的点叫做对称点,对称轴是任何一对对应点所连线段的垂直平分线;
②平面直角坐标系中,已知点A(x1,y1),点B(x2,y2),点C是线段AB的中点,则点C的坐标为;
③将点P(x,y)关于y轴的对称点记作点P1,再将点P1关于直线y=m的对称点记作点P2,则称点P2为点P(x,y)关于y轴和直线y=m的“美对称点”.例如:点P(3,1)关于y轴和直线y=3的“美对称点”为点P2(-3,5).
应用
(1)点A(3,4)关于y轴和直线y=1的“美对称点”A2的坐标是______;
(2)点B(3m+n,m-n)关于y轴和直线y=m的“美对称点”B2的坐标是(-9,5),求m和n的值;
(3)若点C(6x-5,2x+1)关于y轴和直线y=m的“美对称点”C2在第二象限,且满足条件的x的整数解有且只有一个,求m的取值范围.
1.【答案】B
2.【答案】A
3.【答案】A
4.【答案】D
5.【答案】C
6.【答案】B
7.【答案】B
8.【答案】C
9.【答案】C
10.【答案】D
11.【答案】D
12.【答案】A
13.【答案】200
14.【答案】四
15.【答案】全面检查灯泡的使用寿命,具有破坏性
16.【答案】3
17.【答案】班里的同学参加社会实践活动情况;
全班同学.
18.【答案】小雨同学采用的是抽样调查方式;
1000名学生的借书情况是总体;每名学生的借书情况是个体;抽取的100名学生的借书情况是总体的一个样本.
19.【答案】见解析;
(-2,3)或(3,-2).
20.【答案】
21.【答案】50,60;
“阅读”兴趣活动所对应扇形的圆心角的度数为72°;
不能,
理由:∵喜爱“剪纸”兴趣活动的学生的人数,
∴这样的设立计划不能满足所有有意向参加兴趣活动的学生同时进行学习的需求.
22.【答案】40,0.15,12;
;
960人.
23.【答案】3 N(1,2)或N(1,-2) 10
24.【答案】(-3,-2);
m=2,n=3;
.
第1页,共1页
一、选择题:本题共12小题,每小题3分,共36分。在每小题给出的选项中,只有一项是符合题目要求的。
1.根据下列表述,能确定位置的是( )
A. 红星东街 B. 东经106°,北纬32°
C. 太平洋影城3号厅2排 D. 负二层停车场
2.如下表,若田径场的位置可以表示为A1区,则办公楼的位置可以表示为( )
序号 1 2 3 4
A 田径场 喷泉 教学楼 实验楼
B 篮球场 办公楼 食堂 宿舍楼
A. B2区 B. B3区 C. A2区 D. A3区
3.每年的6月6日是全国爱眼日,2023年爱眼日的主题是“关注普遍的眼睛健康”.某中学七年级数学活动兴趣小组为了解该校2000名学生的视力情况,制定了如下调查方案,最合理的方案是( )
A. 按学籍号随机抽取200名学生进行调查 B. 按学籍号随机抽取5名学生进行调查
C. 抽取本校九年级全体学生进行调查 D. 抽取八年级100名女生进行调查
4.若点A(-4,3)与点B关于原点对称,则点B的纵坐标为( )
A. 4 B. -4 C. 3 D. -3
5.某学习小组将要进行一次统计活动,下面是四位同学分别设计的活动序号,其中正确的是( )
A. 实际问题→收集数据→表示数据→整理数据→统计分析合理决策
B. 实际问题→表示数据→收集数据→整理数据→统计分析合理决策
C. 实际问题→收集数据→整理数据→表示数据→统计分析合理决策
D. 实际问题→整理数据→收集数据→表示数据→统计分析合理决策
6.某校为了了解学生在校午餐所需的时间,抽查了20名同学在校午餐所需的时间,获得如下数据(单位:分):10,12,15,10,16,18,19,18,20,34,22,25,20,18,18,20,15,16,21,16.若将这些数据分为5组,则组距是( )
A. 4分 B. 5分 C. 6分 D. 7分
7.如图所示为某地的气候资料,根据图中信息推断,下列说法正确的是( )
A. 夏季高温多雨,冬季寒冷干燥 B. 夏季炎热干燥,冬季温和多雨
C. 冬暖夏凉,降水集中在冬季 D. 冬冷夏热,降水集中在夏季
8.一艘海上搜救船在巡逻过程中发现点A处有一艘故障船发出求救信号,如图8是搜救船上显示的雷达示意图,图上标注了以搜救船点O为中心的等距线(图中所示的同心圆,单位:海里)及角度,要让搜救船在第一时间抵达故障船所在的位置,应该将搜救船的航行方案调整为( )
A. 向北偏西150°方向航行4海里 B. 向南偏西150°方向航行4海里
C. 向北偏西60°方向航行4海里 D. 向南偏东60°方向航行4海里
9.为了解我国总人口变化情况,小祺查阅资料,收集了2016年-2023年连续8年我国总人口变化的数据,并绘制了如图所示的条形统计图.根据统计图,下列推断合理的是( )
A. 2016年-2023年全国总人口数逐渐增长
B. 2016年-2023年全国总人口数逐渐下降
C. 2016年-2023年全国总人口增长数逐渐下降
D. 2016年-2023年全国总人口增长数先增长后下降
10.某班将安全知识竞赛成绩整理后绘制成如图所示的频数分布直方图(每组不包括最小值,包括最大值),图中从左至右前四组的频数占总人数的百分比分别为4%,12%,40%,28%,且第五组的频数是8,下列结论不正确的是( )
A. 第五组的频数占总人数的百分比为16% B. 该班有50名同学参赛
C. 成绩在70~80分的人数最多 D. 80分以上的学生有14名
11.如图,在平面直角坐标系中,点B的坐标是(8,12),点C的坐标是(8,2),AB=AC=13,则点A的坐标是( )
A. (3,6)
B. (-4,5)
C. (-4,6)
D. (-4,7)
12.平面直角坐标系中,我们把横、纵坐标都是整数,且横、纵坐标之和大于0的点称为“和点”.将某“和点”平移,每次平移的方向取决于该点横、纵坐标之和除以4所得的余数(当余数为0时,向右平移;当余数为1时,向上平移;当余数为2时,向左平移;余数为3时,向下平移),每次平移1个单位长度.“和点”P(2,1)按上述规则连续平移3次后,到达点P3(1,1),其平移过程如下:.若“和点”R按上述规则连续平移10次后,到达点R10(7,2),则点R的坐标为( )
A. (12,-3) B. (-9,3) C. (9,-3) D. (-12,3)
二、填空题:本题共4小题,每小题3分,共12分。
13.某校为了解本校1200名学生的周末做家务时间,从中抽查了200名学生的周末做家务时间进行统计,则样本容量为______.
14.已知点P(-4a,2+b)在第三象限,则点Q(a,b)在第______象限.
15.如图是一家灯泡生产厂商的广告图,从统计学角度判断广告语不合适,理由是______.
16.已知A(6,-3),B(-2,4),C(2,-1),,则=______.
三、解答题:本题共8小题,共72分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题7分)
春节过了,你想了解你班里的同学参加社会实践活动情况,你打算实施调查之后再加以总结,那么:
(1)你调查的问题是什么?
(2)你调查的对象是什么?
18.(本小题8分)
小雨同学为调查一个月内全校1000名学生的借书情况,在校园里对学生进行调查,并绘制了如下表格:
借书次数 0 1 2 3 4及4以上
学生人数 45 33 15 5 2
(1)小雨同学采用的是什么调查方式?
(2)总体、个体、样本各是什么?
19.(本小题8分)
你玩过五子棋吗?它的比赛规则是:两人各拥有一种颜色的棋子,每人每次在正方形网格的格点处下一子,两人轮流下,只要连续的同色5个棋子先成一条直线就算胜.如图,是两人玩的一盘棋,若棋盘上白棋①的坐标为(-3,-2),黑棋②的坐标为(-1,0).
(1)请你根据题意,画出相应的平面直角坐标系;
(2)现轮到黑棋下,要使黑棋在这一步要赢,请写出这一步黑棋的坐标.
20.(本小题8分)
在平面直角坐标系中,已知点M(m,2m+3).
(1)若点M在x轴上,则m的值为______;
(2)若点M到x轴、y轴的距离相等,求m的值.
21.(本小题9分)
某校开展了学生的兴趣活动问卷调查,问卷中涉及的兴趣活动有书法、围棋、剪纸、绘画、阅读共五项,参与问卷调查的学生每人必选且只选一项.抽取其中一部分问卷进行整理,分别得到如下统计表和统计图.
学生的兴趣活动统计表
兴趣活动 书法 围棋 剪纸 绘画 阅读
人数 a 30 b 20 40
请根据统计表和统计图提供的信息,解答下列问题:
(1)a= ______,b= ______;
(2)在扇形统计图中,求“阅读”兴趣活动所对应扇形的圆心角的度数;
(3)已知该校共有1200名学生,为使这些学生能够参加自己所喜爱的兴趣活动,该校计划设立5个用于开展不同兴趣活动的专用场地,每个专用场地最多可容纳300人.试问这样的设立计划能否满足所有有意向参加兴趣活动的学生同时进行学习的需求,请说明理由.
22.(本小题9分)
为了解八年级学生每天完成课外作业时间的情况、从全区八年级学生中随机抽取了部分学生每天完成课外作业的时间进行调查,并将调查结果绘制成如下图表:
时间x(小时) 频数y(人数) 频率
0≤x≤0.5 8 0.2
0.5<x≤1 c 0.3
1<x≤1.5 12 0.3
1.5<x≤2 6 b
2<x≤2.5 2 0.05
合计 a 1
(1)a= ______,b= ______,c= ______;
(2)补全频数分布直方图;
(3)根据规定,学生每天完成课外作业的时间不超过1.5小时,那么全区4800名八年级学生中每天完成课外作业时间超过规定的学生约有多少人?
23.(本小题11分)
在数学研究课上,研究小组研究了平面直角坐标系中的特殊线段的长度:在平面直角坐标系中有不重合的两点M(x1,y1)和点N(x2,y2),若x1=x2,则MN∥y轴,且线段MN的长度为|y1-y2|,若y1=y2,则MN∥x轴,且线段MN的长度为|x1-x2|.
【实践操作】
(1)若点M(-1,1),N(2,1),则MN∥x轴,MN的长度为______;若点M(1,0),且MN∥y轴,且MN=2,则点N的坐标为______.
【拓展应用】
(2)如图,在平面直角坐标系中,A(-4,0),B(0,2),C(0,-3).
①如图1,△ABC的面积为______;
②如图2,点D在线段AB上,将点D沿x轴正方向向右平移3个单位长度至E点,若△ACE的面积等于14,求点D坐标.
24.(本小题12分)
阅读理解:
在平面直角坐标系中,经过点M(0,m)且平行于x轴的直线记作直线y=m.
给出如下知识:
①把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线成轴对称,这条直线叫做对称轴,折叠后重合的点叫做对称点,对称轴是任何一对对应点所连线段的垂直平分线;
②平面直角坐标系中,已知点A(x1,y1),点B(x2,y2),点C是线段AB的中点,则点C的坐标为;
③将点P(x,y)关于y轴的对称点记作点P1,再将点P1关于直线y=m的对称点记作点P2,则称点P2为点P(x,y)关于y轴和直线y=m的“美对称点”.例如:点P(3,1)关于y轴和直线y=3的“美对称点”为点P2(-3,5).
应用
(1)点A(3,4)关于y轴和直线y=1的“美对称点”A2的坐标是______;
(2)点B(3m+n,m-n)关于y轴和直线y=m的“美对称点”B2的坐标是(-9,5),求m和n的值;
(3)若点C(6x-5,2x+1)关于y轴和直线y=m的“美对称点”C2在第二象限,且满足条件的x的整数解有且只有一个,求m的取值范围.
1.【答案】B
2.【答案】A
3.【答案】A
4.【答案】D
5.【答案】C
6.【答案】B
7.【答案】B
8.【答案】C
9.【答案】C
10.【答案】D
11.【答案】D
12.【答案】A
13.【答案】200
14.【答案】四
15.【答案】全面检查灯泡的使用寿命,具有破坏性
16.【答案】3
17.【答案】班里的同学参加社会实践活动情况;
全班同学.
18.【答案】小雨同学采用的是抽样调查方式;
1000名学生的借书情况是总体;每名学生的借书情况是个体;抽取的100名学生的借书情况是总体的一个样本.
19.【答案】见解析;
(-2,3)或(3,-2).
20.【答案】
21.【答案】50,60;
“阅读”兴趣活动所对应扇形的圆心角的度数为72°;
不能,
理由:∵喜爱“剪纸”兴趣活动的学生的人数,
∴这样的设立计划不能满足所有有意向参加兴趣活动的学生同时进行学习的需求.
22.【答案】40,0.15,12;
;
960人.
23.【答案】3 N(1,2)或N(1,-2) 10
24.【答案】(-3,-2);
m=2,n=3;
.
第1页,共1页
同课章节目录
