2024-2025学年江苏省淮安市淮安外国语学校八年级(下)月考数学试卷(3月份)(含答案)
文档属性
| 名称 | 2024-2025学年江苏省淮安市淮安外国语学校八年级(下)月考数学试卷(3月份)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 152.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 14:11:57 | ||
图片预览



文档简介
2024-2025学年江苏省淮安外国语学校八年级(下)月考数学试卷(3月份)
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.《国家宝藏》节目立足于中华文化宝库资源,通过对文物的梳理与总结,演绎文物背后的故事与历史,让更多的观众走进博物馆,让一个个馆藏文物鲜活起来.下面四幅图是我国一些博物馆的标志,其中是中心对称图形的是( )
A. B. C. D.
2.下列运算正确的是( )
A. B. C. D.
3.在 ABCD中,∠A与∠B的度数之比为1:2,则∠C的度数是( )
A. 120° B. 100° C. 80° D. 60°
4.在下列根式中,最简二次根式是( )
A. B. C. D.
5.如图,△ABC绕点O逆时针旋转100°后得到△A′B′C′,若∠AOB=35°,则∠A′OB=( )
A. 35°
B. 65°
C. 100°
D. 135°
6.将分式中x与y的值同时扩大为原来的3倍,分式的值( )
A. 扩大3倍 B. 缩小为原来的 C. 不变 D. 无法确定
7.若实数a、b、c依次在数轴上的对应点如图所示,化简的值为( )
A. -a+b-c B. -a-b+c C. a+b-c D. a-b+c
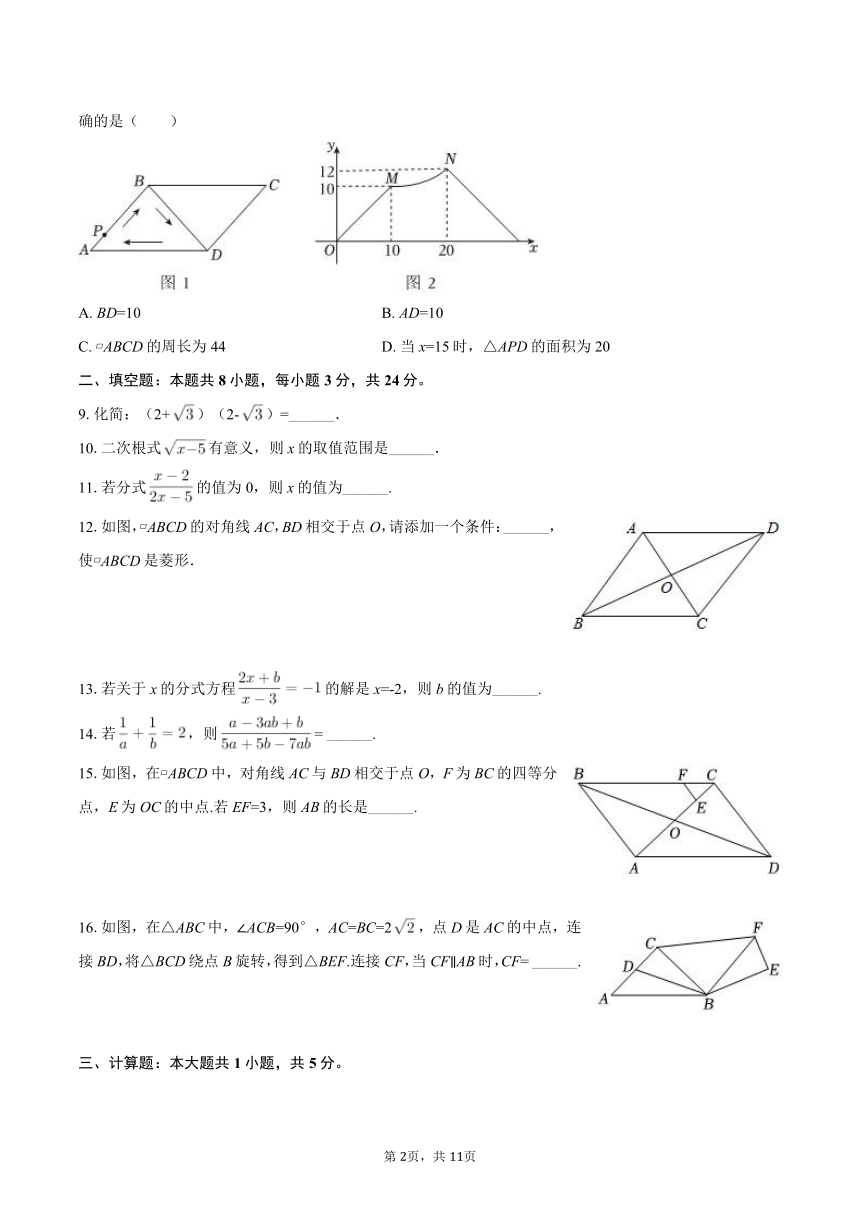
8.如图1,四边形ABCD是平行四边形,连接BD,动点P从点A出发沿折线AB→BD→DA匀速运动,回到点A后停止.设点P运动的路程为x,线段AP的长为y,图2是y与x的函数关系的大致图象,下列结论中不正确的是( )
A. BD=10 B. AD=10
C. ABCD的周长为44 D. 当x=15时,△APD的面积为20
二、填空题:本题共8小题,每小题3分,共24分。
9.化简:(2+)(2-)=______.
10.二次根式有意义,则x的取值范围是______.
11.若分式的值为0,则x的值为______.
12.如图, ABCD的对角线AC,BD相交于点O,请添加一个条件:______,使 ABCD是菱形.
13.若关于x的分式方程的解是x=-2,则b的值为______.
14.若,则= ______.
15.如图,在 ABCD中,对角线AC与BD相交于点O,F为BC的四等分点,E为OC的中点.若EF=3,则AB的长是______.
16.如图,在△ABC中,∠ACB=90°,AC=BC=2,点D是AC的中点,连接BD,将△BCD绕点B旋转,得到△BEF.连接CF,当CF∥AB时,CF= ______.
三、计算题:本大题共1小题,共5分。
17.解分式方程:-1=.
四、解答题:本题共10小题,共97分。解答应写出文字说明,证明过程或演算步骤。
18.(本小题8分)
计算:
(1).
(2).
19.(本小题8分)
先化简,再求值:,其中a是的小数部分.
20.(本小题8分)
已知:如图,在平行四边形ABCD中,E,F分别是边AB,DC上的点,AE=CF,DE⊥AB,求证:四边形DEBF是矩形.
21.(本小题8分)
有一块矩形木板ABCD,木工甲采用如图的方式,将木板的长AD增加,宽AB增加,得到一个面积为128cm2的正方形AEFG.
(1)正方形AEFG的边长为______cm;(填最简二次根式)
(2)求矩形木板ABCD的面积;
(3)木工乙想从矩形木板ABCD中截出长为2.0cm、宽为1.0cm的矩形木条,最多能截出______根这样的木条.
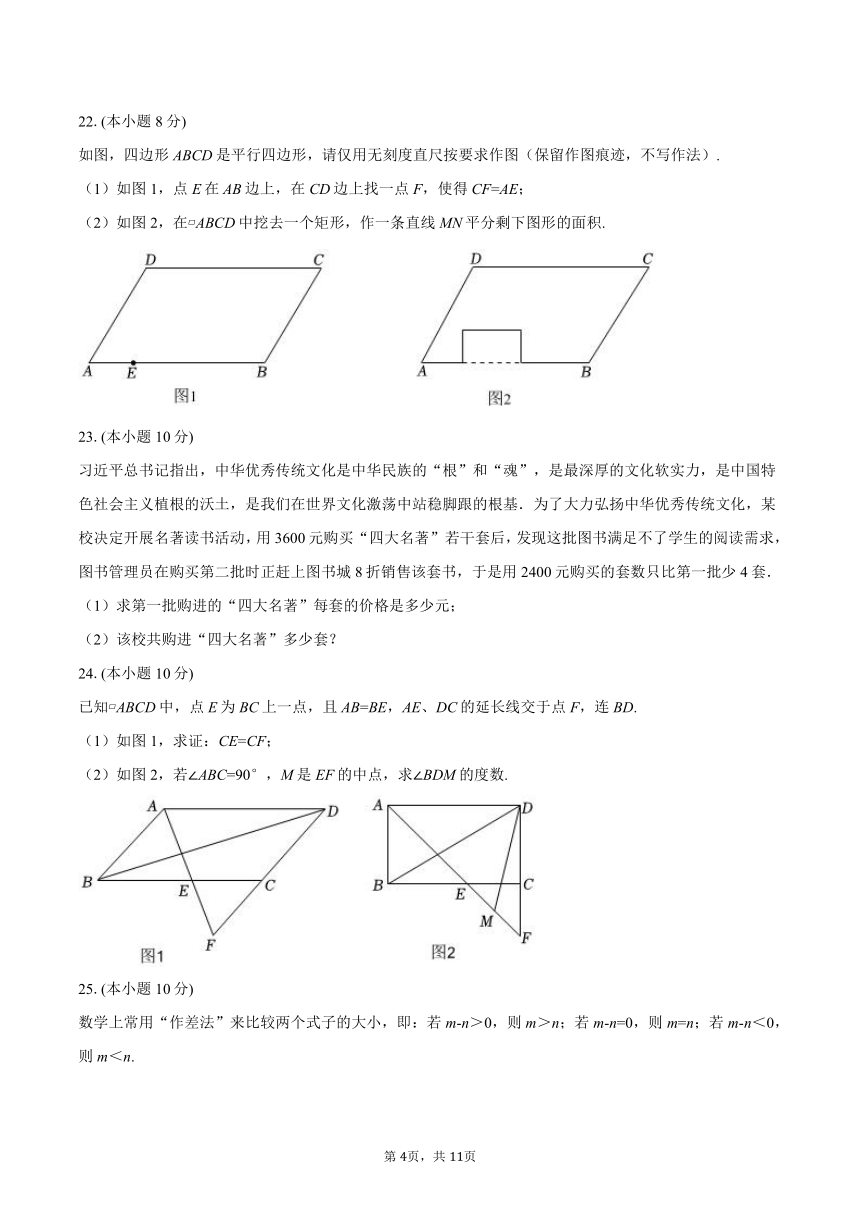
22.(本小题8分)
如图,四边形ABCD是平行四边形,请仅用无刻度直尺按要求作图(保留作图痕迹,不写作法).
(1)如图1,点E在AB边上,在CD边上找一点F,使得CF=AE;
(2)如图2,在 ABCD中挖去一个矩形,作一条直线MN平分剩下图形的面积.
23.(本小题10分)
习近平总书记指出,中华优秀传统文化是中华民族的“根”和“魂”,是最深厚的文化软实力,是中国特色社会主义植根的沃土,是我们在世界文化激荡中站稳脚跟的根基.为了大力弘扬中华优秀传统文化,某校决定开展名著读书活动,用3600元购买“四大名著”若干套后,发现这批图书满足不了学生的阅读需求,图书管理员在购买第二批时正赶上图书城8折销售该套书,于是用2400元购买的套数只比第一批少4套.
(1)求第一批购进的“四大名著”每套的价格是多少元;
(2)该校共购进“四大名著”多少套?
24.(本小题10分)
已知 ABCD中,点E为BC上一点,且AB=BE,AE、DC的延长线交于点F,连BD.
(1)如图1,求证:CE=CF;
(2)如图2,若∠ABC=90°,M是EF的中点,求∠BDM的度数.
25.(本小题10分)
数学上常用“作差法”来比较两个式子的大小,即:若m-n>0,则m>n;若m-n=0,则m=n;若m-n<0,则m<n.
(1)若n>0,试比较与的大小,并说明理由;
(2)某水果店用相同重量的包装盒包装了两款苹果礼盒,售价如表:
连盒重量 售价
甲款礼盒 5kg 50元
乙款礼盒 10kg 100元
请判断哪款礼盒的苹果单价更合算?并说明理由.
26.(本小题13分)
如图1,E,F,G,H四点分别在四边形ABCD的四条边上,若四边形EFGH为菱形,我们称菱形EFGH为四边形ABCD的内接菱形.
(1)如图2,网格中的每个小四边形都为正方形,每个小四边形的顶点叫做格点,由36个小正方形组成一个大正方形ABCD,点E、F在格点上,请在图2中画出四边形ABCD的内接菱形EFGH;
(2)如图3,矩形ABCD中,AB=8,点E在线段AB上且EB=3,四边形EFGH是矩形ABCD的内接菱形,求GC的长度;
(3)如图4,平行四边形ABCD,AB=6,∠B=60°,点E在线段AB上且EB=2,AD=a.
①请你在图4中作出平行四边形ABCD的内接菱形EFGH,点F在边BC上(用直尺和圆规作图,不写作法,保留作图痕迹,标出相应的字母);
②若平行四边形ABCD存在以点E为顶点的内接菱形,则a的取值范围为______.
27.(本小题14分)
【课本再现】
(1)如图1,正方形ABCD的对角线AC、BD相交于点O,正方形A′B′C′D′的顶点A′与点O重合.将正方形A′B′C′D′绕点A′旋转,在这个过程中,若连接EF,则BE、EF、DF之间的数量关系为______.
【类比迁移】
(2)如图2,矩形ABCD对角线的交点O是矩形OB′C′D′的一个顶点,D′O与边AB相交于点E,B′O与边AD相交于点F,连接EF,矩形OB′C′D′可绕着点O旋转,猜想BE,DF,EF之间的数量关系,并进行证明.
【拓展应用】
(3)在菱形ABCD中,∠B=60°,E、F分别是边AB、对角线AC上一点,且AE=AF,以AE、AF为邻边作菱形AEMF,再将菱形AEMF绕点A逆时针旋转一定角度后得到新的菱形AE′M′F′如图3,连接DM′,点P为线段DM′的中点,连接CP、F′P.
①判断CP与F′P的数量关系,并进行证明;
②若AB=4,AE=2,菱形AEMF在旋转过程中,当CP最小时,△CDP的面积为______.
1.【答案】B
2.【答案】D
3.【答案】D
4.【答案】C
5.【答案】B
6.【答案】A
7.【答案】A
8.【答案】B
9.【答案】1
10.【答案】x≥5
11.【答案】2
12.【答案】AD=DC(答案不唯一)
13.【答案】9
14.【答案】
15.【答案】12
16.【答案】2+或-2
17.【答案】解:原方程变形为:-1=,
方程两边同乘3(x+1),得3x-3(x+1)=2x,即3x-3x-3=2x,
解得:x=-1.5,
经检验,x=-1.5是原方程的解.
18.【答案】-2;
-6 ab.
19.【答案】,.
20.【答案】见解析.
21.【答案】8; 12 cm2; 4.
22.【答案】见解析.
23.【答案】解:设第一批购买的“四大名著”每套的价格为x元,则第二批购买的“四大名著”每套的价格为0.8x元,
依题意得:,-=4,
解得:x=150,
经检验,x=150是原方程的解,
答:第一批购进的“四大名著”每套的价格是150元;
(2)由(1)得:=24(套),
∴24+(24-4)=44(套),
答:该校共购进“四大名著”44套.
24.【答案】证明过程见解答;
∠ BDM=45°.
25.【答案】>,理由见解析;
乙款礼盒的苹果单价更合算,理由见解析.
26.【答案】见解析过程;
GC=5;
①见解析过程;
②1+.
27.【答案】∵四边形ABCD是正方形,
∴OB=OC,∠BOC=90°,∠OBC=∠OCE=45°,∠BCD=90°,
∵四边形A′B′C′D′是正方形,
∴∠EOF=90°,
∴∠EOF=∠BOC,
∴∠EOF-∠COE=∠BOC-∠COE,
∴∠BOE=∠COF,
∴△BOE≌△COF(ASA),
∴CF=BE,
同理可得,
CE=DF,
∵CF2+CE2=EF2,
∴BE2+DF2=EF2,
故答案为:BE2+DF2=EF2;
如图1,
延长EO,交CD于G,连接FG,
∵四边形ABCD是矩形,
∴OB=OD,AB∥CD,∠ADC=90°,
∴∠OBE=∠ODC,
∵∠BOE=∠DOG,
∴△DOG≌△BOE(ASA),
∴DG=BE,OE=OG,
∵∠EOF=90°,
∴EF=FG,
∵DF2+DG2=FG2,
∴DF2+BE2=EF2;
①如图2,
CP=F′P,理由如下:
延长F′P至Q,使PQ=F′P,连接CF′,CQ,DQ,
∵点P为线段DM′的中点,
∴PM′=PD,
∵∠DPQ=∠F′PM′,
∴△DPQ≌△M′PF′(SAS),
∴DQ=F′M′,∠PQD=∠M′F′P,
∴DQ∥F′M′,
∵四边形ABCD和四边形AE′M′F′是菱形,
∴AF′=F′M′,AB∥CD,AE′∥F′M′,CD=AD,
∴AE′∥DQ,AF′=DQ,∠BAE′=∠CDQ,
∵∠ADC=∠BAC=∠E′AF′=60°,
∴∠BAE′=CAF′,△ACD是等边三角形,
∴∠CAF′=∠CDQ,∠ACD=60°,AC=CD,
∴△CDQ≌△CAF′(SAS),
∴∠DCQ=∠ACF′,CQ=CF′,
∴∠QCF′=∠ACD=60°,
∴△CQF′是等边三角形,
∴∠CPF′=,CP⊥F′Q,
∴CP=F′P;
②由①知,
∠CPF′=,CP⊥F′Q,
∴CP=CF′,
∵CF′≥AC-AF′=4-2=2,
∴当F′在AC上时,CF′最小,即CP最小,
如图3,
此时M′使BC的中点,作DW⊥BC,交BC的延长线于W,
∵∠W=90°,∠DCW=∠B=60°,CD=4,
∴DW=4,
∴S△DCM′=,
∴S△CDP=S△DCM′=,
故答案为:.
第1页,共1页
一、选择题:本题共8小题,每小题3分,共24分。在每小题给出的选项中,只有一项是符合题目要求的。
1.《国家宝藏》节目立足于中华文化宝库资源,通过对文物的梳理与总结,演绎文物背后的故事与历史,让更多的观众走进博物馆,让一个个馆藏文物鲜活起来.下面四幅图是我国一些博物馆的标志,其中是中心对称图形的是( )
A. B. C. D.
2.下列运算正确的是( )
A. B. C. D.
3.在 ABCD中,∠A与∠B的度数之比为1:2,则∠C的度数是( )
A. 120° B. 100° C. 80° D. 60°
4.在下列根式中,最简二次根式是( )
A. B. C. D.
5.如图,△ABC绕点O逆时针旋转100°后得到△A′B′C′,若∠AOB=35°,则∠A′OB=( )
A. 35°
B. 65°
C. 100°
D. 135°
6.将分式中x与y的值同时扩大为原来的3倍,分式的值( )
A. 扩大3倍 B. 缩小为原来的 C. 不变 D. 无法确定
7.若实数a、b、c依次在数轴上的对应点如图所示,化简的值为( )
A. -a+b-c B. -a-b+c C. a+b-c D. a-b+c
8.如图1,四边形ABCD是平行四边形,连接BD,动点P从点A出发沿折线AB→BD→DA匀速运动,回到点A后停止.设点P运动的路程为x,线段AP的长为y,图2是y与x的函数关系的大致图象,下列结论中不正确的是( )
A. BD=10 B. AD=10
C. ABCD的周长为44 D. 当x=15时,△APD的面积为20
二、填空题:本题共8小题,每小题3分,共24分。
9.化简:(2+)(2-)=______.
10.二次根式有意义,则x的取值范围是______.
11.若分式的值为0,则x的值为______.
12.如图, ABCD的对角线AC,BD相交于点O,请添加一个条件:______,使 ABCD是菱形.
13.若关于x的分式方程的解是x=-2,则b的值为______.
14.若,则= ______.
15.如图,在 ABCD中,对角线AC与BD相交于点O,F为BC的四等分点,E为OC的中点.若EF=3,则AB的长是______.
16.如图,在△ABC中,∠ACB=90°,AC=BC=2,点D是AC的中点,连接BD,将△BCD绕点B旋转,得到△BEF.连接CF,当CF∥AB时,CF= ______.
三、计算题:本大题共1小题,共5分。
17.解分式方程:-1=.
四、解答题:本题共10小题,共97分。解答应写出文字说明,证明过程或演算步骤。
18.(本小题8分)
计算:
(1).
(2).
19.(本小题8分)
先化简,再求值:,其中a是的小数部分.
20.(本小题8分)
已知:如图,在平行四边形ABCD中,E,F分别是边AB,DC上的点,AE=CF,DE⊥AB,求证:四边形DEBF是矩形.
21.(本小题8分)
有一块矩形木板ABCD,木工甲采用如图的方式,将木板的长AD增加,宽AB增加,得到一个面积为128cm2的正方形AEFG.
(1)正方形AEFG的边长为______cm;(填最简二次根式)
(2)求矩形木板ABCD的面积;
(3)木工乙想从矩形木板ABCD中截出长为2.0cm、宽为1.0cm的矩形木条,最多能截出______根这样的木条.
22.(本小题8分)
如图,四边形ABCD是平行四边形,请仅用无刻度直尺按要求作图(保留作图痕迹,不写作法).
(1)如图1,点E在AB边上,在CD边上找一点F,使得CF=AE;
(2)如图2,在 ABCD中挖去一个矩形,作一条直线MN平分剩下图形的面积.
23.(本小题10分)
习近平总书记指出,中华优秀传统文化是中华民族的“根”和“魂”,是最深厚的文化软实力,是中国特色社会主义植根的沃土,是我们在世界文化激荡中站稳脚跟的根基.为了大力弘扬中华优秀传统文化,某校决定开展名著读书活动,用3600元购买“四大名著”若干套后,发现这批图书满足不了学生的阅读需求,图书管理员在购买第二批时正赶上图书城8折销售该套书,于是用2400元购买的套数只比第一批少4套.
(1)求第一批购进的“四大名著”每套的价格是多少元;
(2)该校共购进“四大名著”多少套?
24.(本小题10分)
已知 ABCD中,点E为BC上一点,且AB=BE,AE、DC的延长线交于点F,连BD.
(1)如图1,求证:CE=CF;
(2)如图2,若∠ABC=90°,M是EF的中点,求∠BDM的度数.
25.(本小题10分)
数学上常用“作差法”来比较两个式子的大小,即:若m-n>0,则m>n;若m-n=0,则m=n;若m-n<0,则m<n.
(1)若n>0,试比较与的大小,并说明理由;
(2)某水果店用相同重量的包装盒包装了两款苹果礼盒,售价如表:
连盒重量 售价
甲款礼盒 5kg 50元
乙款礼盒 10kg 100元
请判断哪款礼盒的苹果单价更合算?并说明理由.
26.(本小题13分)
如图1,E,F,G,H四点分别在四边形ABCD的四条边上,若四边形EFGH为菱形,我们称菱形EFGH为四边形ABCD的内接菱形.
(1)如图2,网格中的每个小四边形都为正方形,每个小四边形的顶点叫做格点,由36个小正方形组成一个大正方形ABCD,点E、F在格点上,请在图2中画出四边形ABCD的内接菱形EFGH;
(2)如图3,矩形ABCD中,AB=8,点E在线段AB上且EB=3,四边形EFGH是矩形ABCD的内接菱形,求GC的长度;
(3)如图4,平行四边形ABCD,AB=6,∠B=60°,点E在线段AB上且EB=2,AD=a.
①请你在图4中作出平行四边形ABCD的内接菱形EFGH,点F在边BC上(用直尺和圆规作图,不写作法,保留作图痕迹,标出相应的字母);
②若平行四边形ABCD存在以点E为顶点的内接菱形,则a的取值范围为______.
27.(本小题14分)
【课本再现】
(1)如图1,正方形ABCD的对角线AC、BD相交于点O,正方形A′B′C′D′的顶点A′与点O重合.将正方形A′B′C′D′绕点A′旋转,在这个过程中,若连接EF,则BE、EF、DF之间的数量关系为______.
【类比迁移】
(2)如图2,矩形ABCD对角线的交点O是矩形OB′C′D′的一个顶点,D′O与边AB相交于点E,B′O与边AD相交于点F,连接EF,矩形OB′C′D′可绕着点O旋转,猜想BE,DF,EF之间的数量关系,并进行证明.
【拓展应用】
(3)在菱形ABCD中,∠B=60°,E、F分别是边AB、对角线AC上一点,且AE=AF,以AE、AF为邻边作菱形AEMF,再将菱形AEMF绕点A逆时针旋转一定角度后得到新的菱形AE′M′F′如图3,连接DM′,点P为线段DM′的中点,连接CP、F′P.
①判断CP与F′P的数量关系,并进行证明;
②若AB=4,AE=2,菱形AEMF在旋转过程中,当CP最小时,△CDP的面积为______.
1.【答案】B
2.【答案】D
3.【答案】D
4.【答案】C
5.【答案】B
6.【答案】A
7.【答案】A
8.【答案】B
9.【答案】1
10.【答案】x≥5
11.【答案】2
12.【答案】AD=DC(答案不唯一)
13.【答案】9
14.【答案】
15.【答案】12
16.【答案】2+或-2
17.【答案】解:原方程变形为:-1=,
方程两边同乘3(x+1),得3x-3(x+1)=2x,即3x-3x-3=2x,
解得:x=-1.5,
经检验,x=-1.5是原方程的解.
18.【答案】-2;
-6 ab.
19.【答案】,.
20.【答案】见解析.
21.【答案】8; 12 cm2; 4.
22.【答案】见解析.
23.【答案】解:设第一批购买的“四大名著”每套的价格为x元,则第二批购买的“四大名著”每套的价格为0.8x元,
依题意得:,-=4,
解得:x=150,
经检验,x=150是原方程的解,
答:第一批购进的“四大名著”每套的价格是150元;
(2)由(1)得:=24(套),
∴24+(24-4)=44(套),
答:该校共购进“四大名著”44套.
24.【答案】证明过程见解答;
∠ BDM=45°.
25.【答案】>,理由见解析;
乙款礼盒的苹果单价更合算,理由见解析.
26.【答案】见解析过程;
GC=5;
①见解析过程;
②1+.
27.【答案】∵四边形ABCD是正方形,
∴OB=OC,∠BOC=90°,∠OBC=∠OCE=45°,∠BCD=90°,
∵四边形A′B′C′D′是正方形,
∴∠EOF=90°,
∴∠EOF=∠BOC,
∴∠EOF-∠COE=∠BOC-∠COE,
∴∠BOE=∠COF,
∴△BOE≌△COF(ASA),
∴CF=BE,
同理可得,
CE=DF,
∵CF2+CE2=EF2,
∴BE2+DF2=EF2,
故答案为:BE2+DF2=EF2;
如图1,
延长EO,交CD于G,连接FG,
∵四边形ABCD是矩形,
∴OB=OD,AB∥CD,∠ADC=90°,
∴∠OBE=∠ODC,
∵∠BOE=∠DOG,
∴△DOG≌△BOE(ASA),
∴DG=BE,OE=OG,
∵∠EOF=90°,
∴EF=FG,
∵DF2+DG2=FG2,
∴DF2+BE2=EF2;
①如图2,
CP=F′P,理由如下:
延长F′P至Q,使PQ=F′P,连接CF′,CQ,DQ,
∵点P为线段DM′的中点,
∴PM′=PD,
∵∠DPQ=∠F′PM′,
∴△DPQ≌△M′PF′(SAS),
∴DQ=F′M′,∠PQD=∠M′F′P,
∴DQ∥F′M′,
∵四边形ABCD和四边形AE′M′F′是菱形,
∴AF′=F′M′,AB∥CD,AE′∥F′M′,CD=AD,
∴AE′∥DQ,AF′=DQ,∠BAE′=∠CDQ,
∵∠ADC=∠BAC=∠E′AF′=60°,
∴∠BAE′=CAF′,△ACD是等边三角形,
∴∠CAF′=∠CDQ,∠ACD=60°,AC=CD,
∴△CDQ≌△CAF′(SAS),
∴∠DCQ=∠ACF′,CQ=CF′,
∴∠QCF′=∠ACD=60°,
∴△CQF′是等边三角形,
∴∠CPF′=,CP⊥F′Q,
∴CP=F′P;
②由①知,
∠CPF′=,CP⊥F′Q,
∴CP=CF′,
∵CF′≥AC-AF′=4-2=2,
∴当F′在AC上时,CF′最小,即CP最小,
如图3,
此时M′使BC的中点,作DW⊥BC,交BC的延长线于W,
∵∠W=90°,∠DCW=∠B=60°,CD=4,
∴DW=4,
∴S△DCM′=,
∴S△CDP=S△DCM′=,
故答案为:.
第1页,共1页
同课章节目录
