3.1.2排列与排列数(教学课件)- 高中数学人教B版(2019)选择性必修第二册(共39张PPT)
文档属性
| 名称 | 3.1.2排列与排列数(教学课件)- 高中数学人教B版(2019)选择性必修第二册(共39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-16 22:49:58 | ||
图片预览











文档简介
(共39张PPT)
3.1.2 排列与排列数
第三章 排列、组合与二项式定理
人教B版(2019)
素养目录
02 掌握排列数公式及其推导方法.
01 通过具体实例理解排列、排列数的概念;
新知导入
【尝试与发现】
试解答下列三个计数问题:
(1)小张要在 3 所大学中选择 2 所,分别作为自己的第一志愿和第二志愿,小张共有多少种不同的选择方式?
(2)在 3 名学生中选出 2 名,分别在某话剧表演中扮演 A 和 B 两个角色,共有多少种不同的选择方式?
(3)学校要在 3 名教师中指派 2 人,分别去上海和浙江交流教学经验,共有多少种不同的指派方案?
它们的答案是否一致?
探究新知
以上三个问题虽然实际背景不同,但所求的本质上都是“从 3 个不同对象中选出 2 个并排成先后顺序,有多少种不同的排法”.
因此它们的答案肯定是一致的.
事实上,根据分步计数原理可知,方法种数都是3×2=6种.
一般地,从n个不同对象中,任取m(m≤n)个对象,按照一定顺序排成一列,称为从n个不同对象中取出m个对象的一个排列.
特别地,当m=n时的排列 (即取出所有对象的排列)称为全排列.
特征:①取出的对象互不相同;(互异性)
②取出的对象要按一定的顺序排列.(有序性)
排列
探究新知
【尝试与发现】(1)小张要在 3 所大学中选择 2 所,分别作为自己的第一志愿和第二志愿,小张共有多少种不同的选择方式?
如果用(A,B)表示第一志愿是A,第二志愿是B,则(A,B)就是一个排列.
【思考】(A,B)与(A,C)是相同排列吗?排列(A,B)与(B,A)呢?相同排列有什么特点
两个排列,如果组成排列的对象是相同的,并且对象的排列顺序也相同,那么就称这两个排列是相同的;否则,就称为是不同的.
因此,(A,B)与(A,C)是不同的排列,(A,B)与(B,A)也是不同的排列.
排列数
从n个不同对象中任取m个对象的所有排列的个数,称为从n个不同对象中取出m个对象的排列数.用符号 表示.
注意:(1)所谓排成一列,是指与顺序有关,例如,排列AB与排列BA是不同的排列,可以把一个排列看成一个类似点坐标的有序数对.
(2)符号 中,总要求n和m都是正整数,且m≤n,以后不再声明.
探究新知
思考:排列和排列数有什么区别?
一个排列是指“从n个不同对象中,任取m(m ≤ n)个对象按照一定的顺序排成一列”,它是具体的一种选排情况;
排列数是指“从n个不同对象中任取m(m ≤ n)个对象的所有排列的个数”,它是一个数.
通过探究我们已经知道
【思考】一般情况下, 等于多少呢?
(1) 等于多少?
等于从n个不同对象中取出1个的方法种数,即
(2) 等于多少?
探究新知
等于从n个不同对象中取出2个并排成先后顺序的方法种数.分两步完成:
第一步,选一个排在第一个位置,有n种选法;
第二步,在剩下的对象中选一个排在第二个位置,有n-1种选法.
因此共有n(n-1)种选法,即
探究新知
(3) 等于多少?
(4) 等于多少?
……
思考: 等于多少?
排列数公式:
m个数
例如:
探究新知
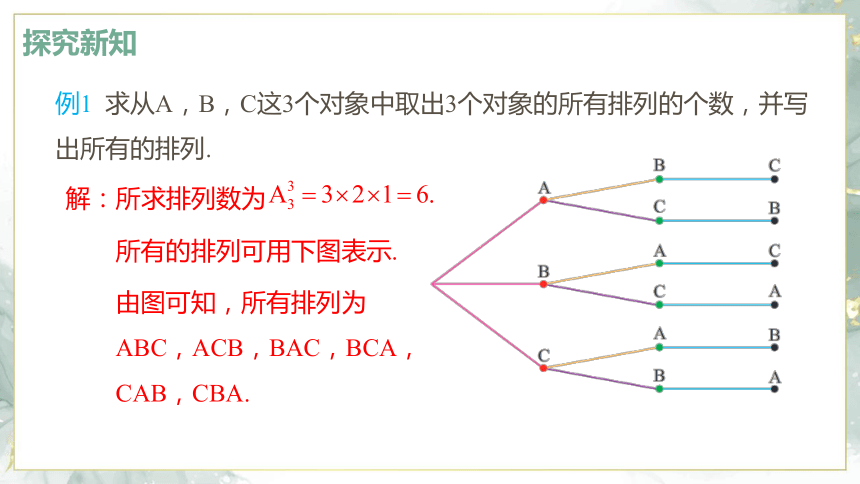
例1 求从A,B,C这3个对象中取出3个对象的所有排列的个数,并写出所有的排列.
解:所求排列数为
所有的排列可用下图表示.
由图可知,所有排列为ABC,ACB,BAC,BCA,CAB,CBA.
通常将上式的右边,从n到1连续n个正整数的乘积简写成:n!
(读作“n的阶乘”).
一般地,在 中,当m=n时,
即
阶乘
探究新知
当0所以此时排列数公式可以改写为:
为了使得上式对m=n时也成立,规定:0!=1 .
另外,为了方便起见,也规定 .
探究新知
例2 求证:
探究新知
思考:假设有n+1个不同对象,甲是其中一个,从这n+1个对象中取出m个做成的排列,可以分为两类:(1)不包括对象甲的;(2)包括对象甲的.
分别计算每一类的排列个数.
(1)若不包括对象甲,则应从余下的n个对象中取出m个对象排成一列,所以有 种方法.
(2)若包括对象甲,分两步完成:
第一步让甲占据一个位置,有m种方法;
第二步,从余下的n个对象中取出m-1个对象占据余下的m-1个位置,有 种方法.根据分步乘法计数原理,共有 种方法.
因此,
探究新知
例3 某地区足球比赛共有12个队伍参加,每队都要与其他各队在主客场分别比赛一次,则共要进行多少场比赛?
解:如果把每一场比赛都看成主场队在前,客场队在后的一个排列,则不难看出,所求比赛数等于从12个对象中取出2个的排列数,即
探究新知
例4 某信号兵用红、黄、蓝三面旗从上到下挂在竖直的旗杆上表示信号,每次可以只挂1面旗,也可以挂2面旗或3面旗,旗数或顺序不同时,表示信号不同,则一共可表示多少种不同的信号?
探究新知
解题过程中,可以将基本计数原理与排列知识有机结合.
解:按照所挂旗数,可以分为三类:
第一类是只挂1面旗,此时可表示 种不同的信号;
第二类是挂2面旗,此时可表示 种不同的信号;
第三类是挂3面旗,此时可表示 种不同的信号 .
按照分类加法计数原理,一共可表示不同的信号
种.
探究新知
例5 用 这10个数字,可以排成多少个没有重复数字的三位数?
解:(方法一)要组成一个没有重复数字的三位数,可以分为两步:
第一步,确定百位上的数字,因为只能是 这9个数字中的某一个,所以有 种方法;
第二步,确定十位和个位上的数字,因为数字不能重复,所以只能从百位以外的数字来选取,因此共有 种方法.
由分步乘法计数原理可知,满足条件的三位数个数为:
.
探究新知
方法二通常称为 "排除法",也就是先算出无限制条件的所有排法种数,然后再减去不符合条件的排法种数.
(方法二)从 这10个数字中,取出3个做排列的排列数为 .
所有的这些排列中,0排在首位的都不能对应一个三位数,而其他的都对应一个三位数.
又因为0排在首位的排列共有 个,
所以可知所求三位数的个数为 .
探究新知
例6 用 0,1,2,…,9 这 10 个数字,可以排成多少个没有重复数字的四位偶数?
解:满足条件的四位数可以分为两类:第一类的末位数字是0,有 个.
第二类的末位数字不是0. 要排成这样的四位数,可以分成三个步骤来完成:
第一步,确定末位数字,因为只能是2,4,6或8,所以有 种方法;
第二步,确定首位数字,因为数字不能重复,所以有 种方法;
第三步,确定中间两位数字,有 种方法. 由分步乘法计数原理可知,这样的数字有 个.
由分类加法计数原理可知,满足条件的四位数个数为:
探究新知
例7 有 3 位男生和 2 位女生,在某风景点前站成一排拍合照,要求 2 位女生要相邻,有多少种不同的站法?
解:分成两步来完成:第一步,先让两位女生站好,有 种方法;
第二步,把两位女生当成一个整体,与3位男生去站成一排,有 种方法.
根据分步乘法计数原理可知,共有 种不同的站法.
例7的解法,相当于把两位女生捆绑在了一起,因此也常被称为“捆绑法”.
探究新知
例8 某晚会要安排3个歌唱节目(记为 A,B,C)和2个舞蹈节目 (记为甲、乙),要求舞蹈节目不能相邻,共有多少种不同的安排方法?
解:分成两步来完成:第一步,先确定3个歌唱节目的先后顺序(不考虑舞蹈节目),总共有 种排法;
第二步,歌唱节目的先后顺序确定之后,舞蹈节目共有 种排法(例如,如果第一步确定的歌唱节目先后顺序为ABC,则舞蹈节目只能安排在如图所示的4个空格中).
由分步乘法计数原理可知,共有 种不同的安排方法.
探究新知
值得注意的是,例8中所有符合条件的安排方法都可用解法中的方式得到,如“AB 甲 C 乙”,只要在图中的第三个、第四个空格分别填上甲、乙即可. 这种解题方法通常称为“插空法”.
在解决类似的要求不相邻的问题中,用插空法往往简单、有效.
C
B
B
B
ACD
72
720
小结
排列数公式:
排列、排列数
排列与排列数
谢谢同学们的聆听
3.1.2 排列与排列数
第三章 排列、组合与二项式定理
人教B版(2019)
素养目录
02 掌握排列数公式及其推导方法.
01 通过具体实例理解排列、排列数的概念;
新知导入
【尝试与发现】
试解答下列三个计数问题:
(1)小张要在 3 所大学中选择 2 所,分别作为自己的第一志愿和第二志愿,小张共有多少种不同的选择方式?
(2)在 3 名学生中选出 2 名,分别在某话剧表演中扮演 A 和 B 两个角色,共有多少种不同的选择方式?
(3)学校要在 3 名教师中指派 2 人,分别去上海和浙江交流教学经验,共有多少种不同的指派方案?
它们的答案是否一致?
探究新知
以上三个问题虽然实际背景不同,但所求的本质上都是“从 3 个不同对象中选出 2 个并排成先后顺序,有多少种不同的排法”.
因此它们的答案肯定是一致的.
事实上,根据分步计数原理可知,方法种数都是3×2=6种.
一般地,从n个不同对象中,任取m(m≤n)个对象,按照一定顺序排成一列,称为从n个不同对象中取出m个对象的一个排列.
特别地,当m=n时的排列 (即取出所有对象的排列)称为全排列.
特征:①取出的对象互不相同;(互异性)
②取出的对象要按一定的顺序排列.(有序性)
排列
探究新知
【尝试与发现】(1)小张要在 3 所大学中选择 2 所,分别作为自己的第一志愿和第二志愿,小张共有多少种不同的选择方式?
如果用(A,B)表示第一志愿是A,第二志愿是B,则(A,B)就是一个排列.
【思考】(A,B)与(A,C)是相同排列吗?排列(A,B)与(B,A)呢?相同排列有什么特点
两个排列,如果组成排列的对象是相同的,并且对象的排列顺序也相同,那么就称这两个排列是相同的;否则,就称为是不同的.
因此,(A,B)与(A,C)是不同的排列,(A,B)与(B,A)也是不同的排列.
排列数
从n个不同对象中任取m个对象的所有排列的个数,称为从n个不同对象中取出m个对象的排列数.用符号 表示.
注意:(1)所谓排成一列,是指与顺序有关,例如,排列AB与排列BA是不同的排列,可以把一个排列看成一个类似点坐标的有序数对.
(2)符号 中,总要求n和m都是正整数,且m≤n,以后不再声明.
探究新知
思考:排列和排列数有什么区别?
一个排列是指“从n个不同对象中,任取m(m ≤ n)个对象按照一定的顺序排成一列”,它是具体的一种选排情况;
排列数是指“从n个不同对象中任取m(m ≤ n)个对象的所有排列的个数”,它是一个数.
通过探究我们已经知道
【思考】一般情况下, 等于多少呢?
(1) 等于多少?
等于从n个不同对象中取出1个的方法种数,即
(2) 等于多少?
探究新知
等于从n个不同对象中取出2个并排成先后顺序的方法种数.分两步完成:
第一步,选一个排在第一个位置,有n种选法;
第二步,在剩下的对象中选一个排在第二个位置,有n-1种选法.
因此共有n(n-1)种选法,即
探究新知
(3) 等于多少?
(4) 等于多少?
……
思考: 等于多少?
排列数公式:
m个数
例如:
探究新知
例1 求从A,B,C这3个对象中取出3个对象的所有排列的个数,并写出所有的排列.
解:所求排列数为
所有的排列可用下图表示.
由图可知,所有排列为ABC,ACB,BAC,BCA,CAB,CBA.
通常将上式的右边,从n到1连续n个正整数的乘积简写成:n!
(读作“n的阶乘”).
一般地,在 中,当m=n时,
即
阶乘
探究新知
当0
为了使得上式对m=n时也成立,规定:0!=1 .
另外,为了方便起见,也规定 .
探究新知
例2 求证:
探究新知
思考:假设有n+1个不同对象,甲是其中一个,从这n+1个对象中取出m个做成的排列,可以分为两类:(1)不包括对象甲的;(2)包括对象甲的.
分别计算每一类的排列个数.
(1)若不包括对象甲,则应从余下的n个对象中取出m个对象排成一列,所以有 种方法.
(2)若包括对象甲,分两步完成:
第一步让甲占据一个位置,有m种方法;
第二步,从余下的n个对象中取出m-1个对象占据余下的m-1个位置,有 种方法.根据分步乘法计数原理,共有 种方法.
因此,
探究新知
例3 某地区足球比赛共有12个队伍参加,每队都要与其他各队在主客场分别比赛一次,则共要进行多少场比赛?
解:如果把每一场比赛都看成主场队在前,客场队在后的一个排列,则不难看出,所求比赛数等于从12个对象中取出2个的排列数,即
探究新知
例4 某信号兵用红、黄、蓝三面旗从上到下挂在竖直的旗杆上表示信号,每次可以只挂1面旗,也可以挂2面旗或3面旗,旗数或顺序不同时,表示信号不同,则一共可表示多少种不同的信号?
探究新知
解题过程中,可以将基本计数原理与排列知识有机结合.
解:按照所挂旗数,可以分为三类:
第一类是只挂1面旗,此时可表示 种不同的信号;
第二类是挂2面旗,此时可表示 种不同的信号;
第三类是挂3面旗,此时可表示 种不同的信号 .
按照分类加法计数原理,一共可表示不同的信号
种.
探究新知
例5 用 这10个数字,可以排成多少个没有重复数字的三位数?
解:(方法一)要组成一个没有重复数字的三位数,可以分为两步:
第一步,确定百位上的数字,因为只能是 这9个数字中的某一个,所以有 种方法;
第二步,确定十位和个位上的数字,因为数字不能重复,所以只能从百位以外的数字来选取,因此共有 种方法.
由分步乘法计数原理可知,满足条件的三位数个数为:
.
探究新知
方法二通常称为 "排除法",也就是先算出无限制条件的所有排法种数,然后再减去不符合条件的排法种数.
(方法二)从 这10个数字中,取出3个做排列的排列数为 .
所有的这些排列中,0排在首位的都不能对应一个三位数,而其他的都对应一个三位数.
又因为0排在首位的排列共有 个,
所以可知所求三位数的个数为 .
探究新知
例6 用 0,1,2,…,9 这 10 个数字,可以排成多少个没有重复数字的四位偶数?
解:满足条件的四位数可以分为两类:第一类的末位数字是0,有 个.
第二类的末位数字不是0. 要排成这样的四位数,可以分成三个步骤来完成:
第一步,确定末位数字,因为只能是2,4,6或8,所以有 种方法;
第二步,确定首位数字,因为数字不能重复,所以有 种方法;
第三步,确定中间两位数字,有 种方法. 由分步乘法计数原理可知,这样的数字有 个.
由分类加法计数原理可知,满足条件的四位数个数为:
探究新知
例7 有 3 位男生和 2 位女生,在某风景点前站成一排拍合照,要求 2 位女生要相邻,有多少种不同的站法?
解:分成两步来完成:第一步,先让两位女生站好,有 种方法;
第二步,把两位女生当成一个整体,与3位男生去站成一排,有 种方法.
根据分步乘法计数原理可知,共有 种不同的站法.
例7的解法,相当于把两位女生捆绑在了一起,因此也常被称为“捆绑法”.
探究新知
例8 某晚会要安排3个歌唱节目(记为 A,B,C)和2个舞蹈节目 (记为甲、乙),要求舞蹈节目不能相邻,共有多少种不同的安排方法?
解:分成两步来完成:第一步,先确定3个歌唱节目的先后顺序(不考虑舞蹈节目),总共有 种排法;
第二步,歌唱节目的先后顺序确定之后,舞蹈节目共有 种排法(例如,如果第一步确定的歌唱节目先后顺序为ABC,则舞蹈节目只能安排在如图所示的4个空格中).
由分步乘法计数原理可知,共有 种不同的安排方法.
探究新知
值得注意的是,例8中所有符合条件的安排方法都可用解法中的方式得到,如“AB 甲 C 乙”,只要在图中的第三个、第四个空格分别填上甲、乙即可. 这种解题方法通常称为“插空法”.
在解决类似的要求不相邻的问题中,用插空法往往简单、有效.
C
B
B
B
ACD
72
720
小结
排列数公式:
排列、排列数
排列与排列数
谢谢同学们的聆听
