【导学案】第11章 平面直角坐标系复习课(含答案) 2025-2026学年数学沪科版(2024)八年级上册
文档属性
| 名称 | 【导学案】第11章 平面直角坐标系复习课(含答案) 2025-2026学年数学沪科版(2024)八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 486.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 17:44:34 | ||
图片预览

文档简介
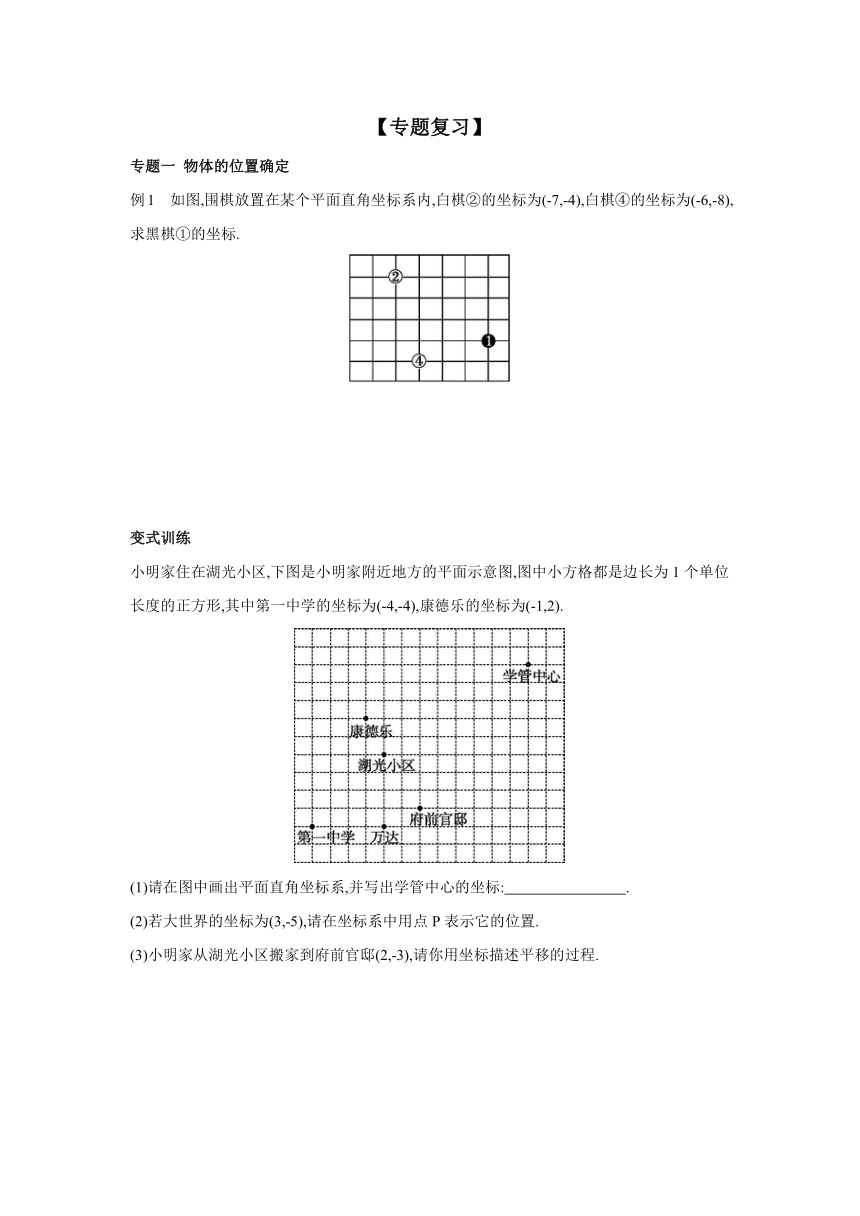
第11章 平面直角坐标系 复习课
复习目标
1.能画出平面直角坐标系,会在平面直角坐标系中描点,能写出平面直角坐标系中点的坐标.
2.知道平面直角坐标系中的点与有序实数对的一一对应关系,体会数形结合的思想.
3.掌握平面直角坐标系中图形的平移与坐标的变化规律.
重点
平面直角坐标系中的点与平移.
【体系构建】
【专题复习】
专题一 物体的位置确定
例1 如图,围棋放置在某个平面直角坐标系内,白棋②的坐标为(-7,-4),白棋④的坐标为(-6,-8),求黑棋①的坐标.
变式训练
小明家住在湖光小区,下图是小明家附近地方的平面示意图,图中小方格都是边长为1个单位长度的正方形,其中第一中学的坐标为(-4,-4),康德乐的坐标为(-1,2).
(1)请在图中画出平面直角坐标系,并写出学管中心的坐标: .
(2)若大世界的坐标为(3,-5),请在坐标系中用点P表示它的位置.
(3)小明家从湖光小区搬家到府前官邸(2,-3),请你用坐标描述平移的过程.
专题二 点的坐标特征
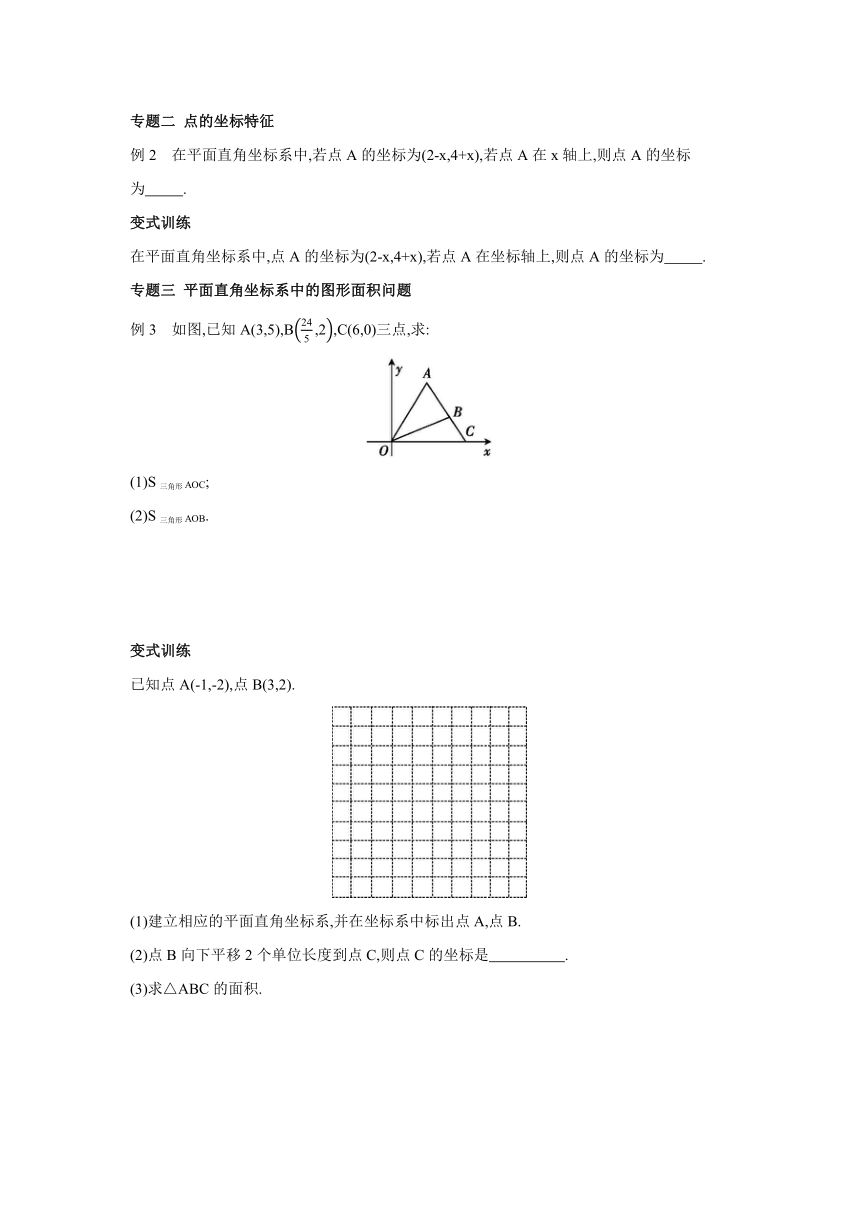
例2 在平面直角坐标系中,若点A的坐标为(2-x,4+x),若点A在x轴上,则点A的坐标为 .
变式训练
在平面直角坐标系中,点A的坐标为(2-x,4+x),若点A在坐标轴上,则点A的坐标为 .
专题三 平面直角坐标系中的图形面积问题
例3 如图,已知A(3,5),B,C(6,0)三点,求:
(1)S三角形AOC;
(2)S三角形AOB.
变式训练
已知点A(-1,-2),点B(3,2).
(1)建立相应的平面直角坐标系,并在坐标系中标出点A,点B.
(2)点B向下平移2个单位长度到点C,则点C的坐标是 .
(3)求△ABC的面积.
专题四 平面直角坐标系中图形的平移
例4 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,三角形ABC的顶点均在格点上,点C的坐标为(4,-1).把三角形ABC向上平移5个单位长度后得到对应的三角形A1B1C1,求出C1的坐标,并画出三角形A1B1C1.
变式训练
1.如图,在平面直角坐标系中,点A,B,P的坐标分别为(3,0),(0,2),(1,4).若AB∥PQ,且AB=PQ,则点Q的坐标是 ( )
A.(-2,6)或(4,2)
B.(-2,6)或(5,1)
C.(4,2)
D.(5,1)
2.△ABC与△A'B'Cv在平面直角坐标系中的位置如图所示.
(1)分别写出下列各点的坐标:A ,A' .
(2)若P(x,y)是△ABC内部一点,则△A'B'C'内部的对应点P'的坐标为 .
(3)△A'B'C'是由△ABC经过怎样的平移得到的
参考答案
专题复习
专题一
例1
解:由白棋④的坐标为(-6,-8),而黑棋①在白棋④的上方一格,所以黑棋①的纵坐标为-7,黑棋①在白棋④右侧三格,所以黑棋①的横坐标为-3,即黑棋①的坐标为(-3,-7).
变式训练
解:(1)如图所示.(8,5).
(2)如图所示:
(3)用坐标描述平移的过程为(0,0)→(2,0)→(2,-3)(答案不唯一).
专题二
例2
(6,0)
变式训练
(6,0)或(0,6)
专题三
例3
解:(1)由图可知,三角形AOC的底边长为6,底边上的高为5,所以S三角形AOC=×6×5=15.
(2)=-=15-×6×2=9.
变式训练
解:(1)如图1所示.
图1
(2)(3,0).
(3)如图2所示.
图2
S△ABC=×2×4=4.
专题四
例4
解:由图可知,点A的坐标为(1,-4),点B的坐标为(5,-4),则向上平移5个单位长度后,点C的对应点C1的坐标为(4,4),点B的对应点B1的坐标为(5,1),点A的对应点A1的坐标为(1,1),这样就可以画出三角形A1B1C1.
变式训练
1.A
2.解:(1)(1,3);(-3,1).
(2)(x-4,y-2).
(3)△ABC向左平移4个单位长度,再向下平移2个单位长度得到△A'B'C'.
复习目标
1.能画出平面直角坐标系,会在平面直角坐标系中描点,能写出平面直角坐标系中点的坐标.
2.知道平面直角坐标系中的点与有序实数对的一一对应关系,体会数形结合的思想.
3.掌握平面直角坐标系中图形的平移与坐标的变化规律.
重点
平面直角坐标系中的点与平移.
【体系构建】
【专题复习】
专题一 物体的位置确定
例1 如图,围棋放置在某个平面直角坐标系内,白棋②的坐标为(-7,-4),白棋④的坐标为(-6,-8),求黑棋①的坐标.
变式训练
小明家住在湖光小区,下图是小明家附近地方的平面示意图,图中小方格都是边长为1个单位长度的正方形,其中第一中学的坐标为(-4,-4),康德乐的坐标为(-1,2).
(1)请在图中画出平面直角坐标系,并写出学管中心的坐标: .
(2)若大世界的坐标为(3,-5),请在坐标系中用点P表示它的位置.
(3)小明家从湖光小区搬家到府前官邸(2,-3),请你用坐标描述平移的过程.
专题二 点的坐标特征
例2 在平面直角坐标系中,若点A的坐标为(2-x,4+x),若点A在x轴上,则点A的坐标为 .
变式训练
在平面直角坐标系中,点A的坐标为(2-x,4+x),若点A在坐标轴上,则点A的坐标为 .
专题三 平面直角坐标系中的图形面积问题
例3 如图,已知A(3,5),B,C(6,0)三点,求:
(1)S三角形AOC;
(2)S三角形AOB.
变式训练
已知点A(-1,-2),点B(3,2).
(1)建立相应的平面直角坐标系,并在坐标系中标出点A,点B.
(2)点B向下平移2个单位长度到点C,则点C的坐标是 .
(3)求△ABC的面积.
专题四 平面直角坐标系中图形的平移
例4 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,在建立平面直角坐标系后,三角形ABC的顶点均在格点上,点C的坐标为(4,-1).把三角形ABC向上平移5个单位长度后得到对应的三角形A1B1C1,求出C1的坐标,并画出三角形A1B1C1.
变式训练
1.如图,在平面直角坐标系中,点A,B,P的坐标分别为(3,0),(0,2),(1,4).若AB∥PQ,且AB=PQ,则点Q的坐标是 ( )
A.(-2,6)或(4,2)
B.(-2,6)或(5,1)
C.(4,2)
D.(5,1)
2.△ABC与△A'B'Cv在平面直角坐标系中的位置如图所示.
(1)分别写出下列各点的坐标:A ,A' .
(2)若P(x,y)是△ABC内部一点,则△A'B'C'内部的对应点P'的坐标为 .
(3)△A'B'C'是由△ABC经过怎样的平移得到的
参考答案
专题复习
专题一
例1
解:由白棋④的坐标为(-6,-8),而黑棋①在白棋④的上方一格,所以黑棋①的纵坐标为-7,黑棋①在白棋④右侧三格,所以黑棋①的横坐标为-3,即黑棋①的坐标为(-3,-7).
变式训练
解:(1)如图所示.(8,5).
(2)如图所示:
(3)用坐标描述平移的过程为(0,0)→(2,0)→(2,-3)(答案不唯一).
专题二
例2
(6,0)
变式训练
(6,0)或(0,6)
专题三
例3
解:(1)由图可知,三角形AOC的底边长为6,底边上的高为5,所以S三角形AOC=×6×5=15.
(2)=-=15-×6×2=9.
变式训练
解:(1)如图1所示.
图1
(2)(3,0).
(3)如图2所示.
图2
S△ABC=×2×4=4.
专题四
例4
解:由图可知,点A的坐标为(1,-4),点B的坐标为(5,-4),则向上平移5个单位长度后,点C的对应点C1的坐标为(4,4),点B的对应点B1的坐标为(5,1),点A的对应点A1的坐标为(1,1),这样就可以画出三角形A1B1C1.
变式训练
1.A
2.解:(1)(1,3);(-3,1).
(2)(x-4,y-2).
(3)△ABC向左平移4个单位长度,再向下平移2个单位长度得到△A'B'C'.
