2024新人教版七年级上数学 3.2 代数式的值 第2课时 几何中的代数式求值 课件(共30张PPT)
文档属性
| 名称 | 2024新人教版七年级上数学 3.2 代数式的值 第2课时 几何中的代数式求值 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 00:00:00 | ||
图片预览








文档简介
(共30张PPT)
人教版(2024)
七年级上册
3.2 代数式的值
第2课时 几何中的代数式求值
第三章 · 代数式
几何中的代数式求值
知识目标
1.理解几何图形中线段长度、面积等量化指标与代数式的对应关系;
2.掌握用字母表示几何元素,并代入具体数值计算代数式的值;
3.熟练进行“几何语言→符号化表达→数值代入→结果验证”的完整流程.
能力目标
1.强化单位换算意识、精确计算习惯;
2.培养分步书写规范性,明确标注每一步骤的几何依据;
3.借助网格纸手绘示意图辅助分析复杂图形.
素质目标
1.感知数学知识与实际生活的普遍联系;
2.培养学生的探索能力和进取精神;
3.体会数学建模在解决实际问题中的作用.
教学难点
教学重点
实现数、形的有效转换,即准确提取几何特征并用代数语言描述
几何语言→符号化表达→数值代入→结果验证
情景导入
1
合作探究
2
抽象概括
3
示范讲解
4
课堂练习
5
课堂小结
6
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
回顾:求代数式的值
一般地,用数值代替代数式中的字母,按照代数式中的运算关系计算得出的结果,叫作代数式的值.
注意:1.当字母取不同的数值时,代数式的值一般也不同.
2.代数式里的字母可以取各种不同的数值,但所取的数值必须使代数式和它表示的实际数量有意义,如上例5n+20中的字母n不能取负数,也不能取小数.
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
回顾:代数式的值的基本方法和步骤
例:根据下列x,y的值,分别求代数式2x+3y的值:
x=15,y=12;
解:当x=15,y=12时,
2x+3y
=2×15+3×12
=30+36
=66;
求代数式的值的步骤:
(1)写出条件:当……时.
(2)抄写代数式.
(3)代入数值.
(4)计算得出结果.
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
以下是校园绿化带规划的方案,你能回忆起以下图形面积与周长的计算公式吗?
圆形
长方形
正方形
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
复习旧知
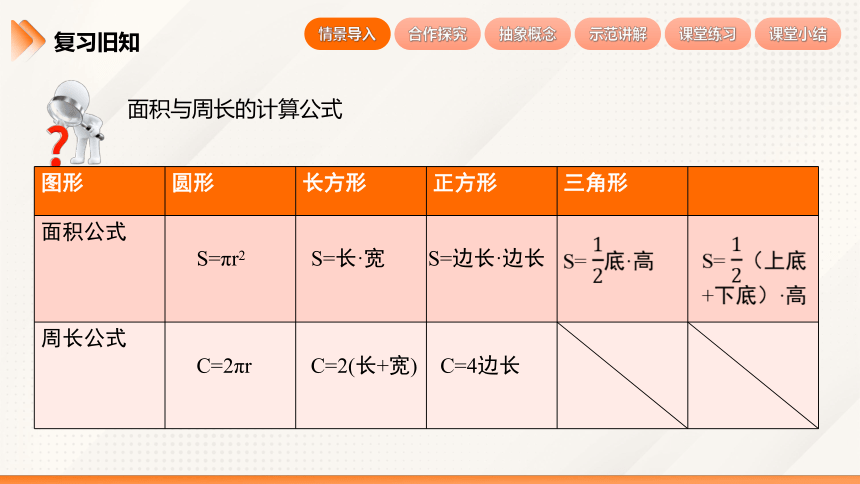
面积与周长的计算公式
图形 圆形 长方形 正方形 三角形
面积公式
周长公式
C=2(长+宽)
S=长·宽
C=4边长
S=边长·边长
C=2πr
S=πr2
S= 底·高
S= (上底+下底)·高
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
复习旧知
体积的计算公式
长方形:
正方形:
V = 长·宽·高
V = 棱长·棱长·棱长
分析问题,寻找对应
体会几何中的代数式求值过程.
探究
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
如图,用字母表示图中阴影部分的面积:
m
n
p
q
分析:阴影的面积 = 大矩形的面积 - 小矩形的面积.
S = mn - pq.
分析问题,寻找对应
体会几何中的代数式求值过程.
探究
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
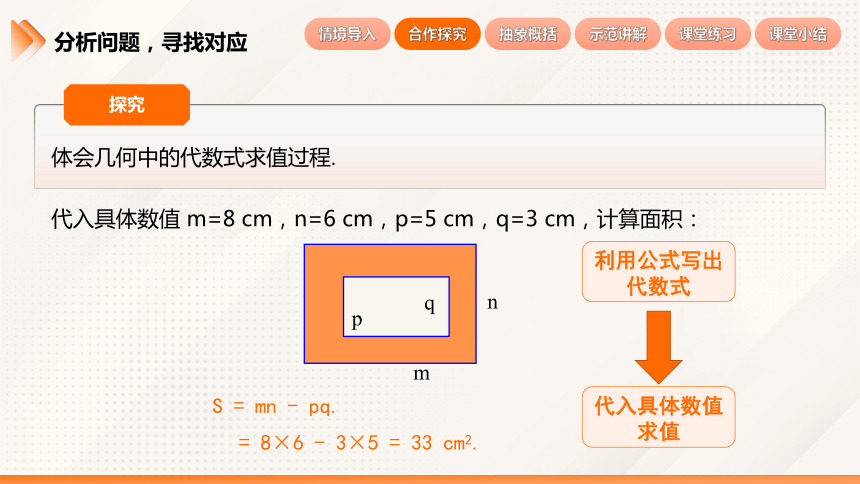
代入具体数值 m=8 cm,n=6 cm,p=5 cm,q=3 cm,计算面积:
n
m
q
p
= 8×6 - 3×5 = 33 cm2.
S = mn - pq.
利用公式写出代数式
代入具体数值求值
几何中的代数式求值
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
几何中的代数式求值的步骤
第一步,利用公式写出代数式
第二步,代入具体数值求值
几何中的代数式求值
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
特别提醒
用代数式解决与图形面积有关的问题时,通常将图形分解成几部分,根据它们的构成利用和差关系求解.
对于不能直接求得的图形面积,常运用转化思想将其转化成其他规则图形面积的和或差进行求解.
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例1
如图,某学校操场最内侧的跑道由两段直道和两段半圆形的弯道组成,其中直道的长为 a,半圆形弯道的直径为 b.
(1)用代数式表示这条跑道的周长;
(2)当a = 67.3 m,b = 52.6 m 时,求这条跑道的周长(π取3.14,结果取整数).
分析:跑道的周长是两段直道和两段弯道的长度和.由圆的周长公式可以求出弯道的长度.
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例1
如图,某学校操场最内侧的跑道由两段直道和两段半圆形的弯道组成,其中直道的长为 a,半圆形弯道的直径为 b.
(1)用代数式表示这条跑道的周长;
(2)当a = 67.3 m,b = 52.6 m 时,求这条跑道的周长(π取3.14,结果取整数).
解
(1)两段直道的长为 2a;
两段弯道组成一个圆,
它的直径为 b,周长为 πb.
因此,这条跑道的周长为 2a + πb.
b
a
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例1
如图,某学校操场最内侧的跑道由两段直道和两段半圆形的弯道组成,其中直道的长为 a,半圆形弯道的直径为 b.
(1)用代数式表示这条跑道的周长;
(2)当a = 67.3 m,b = 52.6 m 时,求这条跑道的周长(π取3.14,结果取整数).
解
(2)当 a = 67.3 m,b = 52.6 m 时,
2a + πb = 2×67.3 + 3.14×52.6
≈ 300(m)
因此,这条跑道的周长约为 300 m.
b
a
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例2
一个三角尺的形状和尺寸如图所示,用代数式表示这个三角尺的面积 S.当 a = 10 cm,b = 17.3 cm,r = 2 cm 时,求这个三角尺的面积(π 取 3.14)
r
a
b
分析:三角尺的面积 = 三角形的面积 - 圆的面积.根据三角形、圆的面积公式可以求出三角尺的面积.
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例2
一个三角尺的形状和尺寸如图所示,用代数式表示这个三角尺的面积 S.当 a = 10 cm,b = 17.3 cm,r = 2 cm 时,求这个三角尺的面积(π 取 3.14)
r
a
b
解
三角形的面积为ab,圆的面积为πr ,S=ab - πr2 .
当a=10 cm,b=17.3 cm,r=2 cm时,
因此,这个三角尺的面积是73.94 cm2.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.如图是一个长为 x,宽为 y 的长方形休闲广场,在它的四角各修建一块半径为 r 的四分之一圆形的花坛(阴影部分),其余部分作为休闲区.
(1)用代数式表示休闲区的面积;
(2)若长方形休闲广场的长为 50 m,宽为 20 m,四分之一圆形花坛的半径为 8 m,求休闲区的面积(π 取3.14,结果取整数).
分析:花坛的面积=4×圆的面积.休闲区的面积 = 长方形休闲广场的面积-花坛的面积.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.如图是一个长为 x,宽为 y 的长方形休闲广场,在它的四角各修建一块半径为 r 的四分之一圆形的花坛(阴影部分),其余部分作为休闲区.
(1)用代数式表示休闲区的面积;
(2)若长方形休闲广场的长为 50 m,宽为 20 m,四分之一圆形花坛的半径为 8 m,求休闲区的面积(π 取3.14,结果取整数).
解:(1)休闲区的面积 S = xy - πr2.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.如图是一个长为 x,宽为 y 的长方形休闲广场,在它的四角各修建一块半径为 r 的四分之一圆形的花坛(阴影部分),其余部分作为休闲区.
(2)若长方形休闲广场的长为 50 m,宽为 20 m,四分之一圆形花坛的半径为 8 m,求休闲区的面积(π 取3.14,结果取整数).
解:(2)当x = 50 m,y = 20 m,r = 8 m 时,
S = xy - πr2 = 50×20 - 3.14×82 ≈ 799 (m2).
因此,休闲区的面积约为 799 m2.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
2.填空题.
(1)若 a,b 分别表示平行四边形的底和高,则面积S =_____;当 a = 2 cm,b = 3 cm 时,S =____cm2.
ab
6
(2)若 a,b 分别表示梯形的上底和下底,h 表示梯形的高,则面积 S =_________;当 a = 2 cm,b = 4 cm,h = 5 cm 时,S =________cm2.
15
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
3.一个长方体纸箱的长是a,宽与高都是b,用代数式表示这个纸箱的体积V.当a=60 cm,b=40 cm时,求这个纸箱的体积.
解:这个纸箱的体积V=a·b·b=a·b2.
当a=60 cm,b=40 cm时,
这个纸箱的体积V=60×40×40=96000.
答:这个纸箱的体积V=a·b2.
当a=60 cm,b=40 cm时,这个纸箱的体积是96000 cm3.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
4.如图,用代数式表示圆环的面积.当 R = 15 cm,r = 10 cm 时,求圆环的面积(π 取 3.14).
解:圆环的面积为 πR2 - πr2 .
当 R = 15 cm,r = 10 cm 时,
πR2 – πr2 = 3.14×152 - 3.14×102 = 392.5 (cm2).
因此,圆环的面积为392.5 cm2 .
对应中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.(2025·湖北·中考真题)一个矩形相邻两边的长分别为2,m,则这个矩形的面积是______.
[答案]2m
[分析]该题考查了列代数式,根据矩形的性质求面积,根据矩形的面积是长×宽即可解答.
[详解]解:根据题意可得矩形的面积是2m,
故答案为:2m.
对应中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
2.(2024·四川雅安·中考真题) 如图是1个纸杯和若干个叠放在一起的纸杯的示意图,在探究纸杯叠放在一起后的总高度H与杯子数量n的变化规律的活动中,我们可以获得以下数据(字母),请选用适当的字母表示______.
①杯子底部到杯沿底边的高h;②杯口直径D;③杯底直径d;④杯沿高a.
[答案]h+an
[分析]本题考查的是列代数式,由总高度=等于杯子底部到杯沿底边的高h加上n个杯子的杯沿高na即可得到答案;
[详解]解:由题意可得:H=h+an,
故答案为:h+an;
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
我亲历了什么
我知道了什么
我会什么
几何中的代数式求值的步骤
求解几何中的代数式求值的应用题
数、形的有效转换
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
几何中的代数式求值的步骤
第一步,利用公式写出代数式
第二步,代入具体数值求值
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
特别提醒
用代数式解决与图形面积有关的问题时,通常将图形分解成几部分,根据它们的构成利用和差关系求解.
对于不能直接求得的图形面积,常运用转化思想将其转化成其他规则图形面积的和或差进行求解.
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
课后作业
A层:P82:习题3.2:第3题,第4题;
B层:P82:习题3.2:第6题,第7题.
下 课
人教版(2024)
七年级上册
3.2 代数式的值
第2课时 几何中的代数式求值
第三章 · 代数式
几何中的代数式求值
知识目标
1.理解几何图形中线段长度、面积等量化指标与代数式的对应关系;
2.掌握用字母表示几何元素,并代入具体数值计算代数式的值;
3.熟练进行“几何语言→符号化表达→数值代入→结果验证”的完整流程.
能力目标
1.强化单位换算意识、精确计算习惯;
2.培养分步书写规范性,明确标注每一步骤的几何依据;
3.借助网格纸手绘示意图辅助分析复杂图形.
素质目标
1.感知数学知识与实际生活的普遍联系;
2.培养学生的探索能力和进取精神;
3.体会数学建模在解决实际问题中的作用.
教学难点
教学重点
实现数、形的有效转换,即准确提取几何特征并用代数语言描述
几何语言→符号化表达→数值代入→结果验证
情景导入
1
合作探究
2
抽象概括
3
示范讲解
4
课堂练习
5
课堂小结
6
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
回顾:求代数式的值
一般地,用数值代替代数式中的字母,按照代数式中的运算关系计算得出的结果,叫作代数式的值.
注意:1.当字母取不同的数值时,代数式的值一般也不同.
2.代数式里的字母可以取各种不同的数值,但所取的数值必须使代数式和它表示的实际数量有意义,如上例5n+20中的字母n不能取负数,也不能取小数.
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
回顾:代数式的值的基本方法和步骤
例:根据下列x,y的值,分别求代数式2x+3y的值:
x=15,y=12;
解:当x=15,y=12时,
2x+3y
=2×15+3×12
=30+36
=66;
求代数式的值的步骤:
(1)写出条件:当……时.
(2)抄写代数式.
(3)代入数值.
(4)计算得出结果.
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
以下是校园绿化带规划的方案,你能回忆起以下图形面积与周长的计算公式吗?
圆形
长方形
正方形
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
复习旧知
面积与周长的计算公式
图形 圆形 长方形 正方形 三角形
面积公式
周长公式
C=2(长+宽)
S=长·宽
C=4边长
S=边长·边长
C=2πr
S=πr2
S= 底·高
S= (上底+下底)·高
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
复习旧知
体积的计算公式
长方形:
正方形:
V = 长·宽·高
V = 棱长·棱长·棱长
分析问题,寻找对应
体会几何中的代数式求值过程.
探究
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
如图,用字母表示图中阴影部分的面积:
m
n
p
q
分析:阴影的面积 = 大矩形的面积 - 小矩形的面积.
S = mn - pq.
分析问题,寻找对应
体会几何中的代数式求值过程.
探究
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
代入具体数值 m=8 cm,n=6 cm,p=5 cm,q=3 cm,计算面积:
n
m
q
p
= 8×6 - 3×5 = 33 cm2.
S = mn - pq.
利用公式写出代数式
代入具体数值求值
几何中的代数式求值
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
几何中的代数式求值的步骤
第一步,利用公式写出代数式
第二步,代入具体数值求值
几何中的代数式求值
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
特别提醒
用代数式解决与图形面积有关的问题时,通常将图形分解成几部分,根据它们的构成利用和差关系求解.
对于不能直接求得的图形面积,常运用转化思想将其转化成其他规则图形面积的和或差进行求解.
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例1
如图,某学校操场最内侧的跑道由两段直道和两段半圆形的弯道组成,其中直道的长为 a,半圆形弯道的直径为 b.
(1)用代数式表示这条跑道的周长;
(2)当a = 67.3 m,b = 52.6 m 时,求这条跑道的周长(π取3.14,结果取整数).
分析:跑道的周长是两段直道和两段弯道的长度和.由圆的周长公式可以求出弯道的长度.
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例1
如图,某学校操场最内侧的跑道由两段直道和两段半圆形的弯道组成,其中直道的长为 a,半圆形弯道的直径为 b.
(1)用代数式表示这条跑道的周长;
(2)当a = 67.3 m,b = 52.6 m 时,求这条跑道的周长(π取3.14,结果取整数).
解
(1)两段直道的长为 2a;
两段弯道组成一个圆,
它的直径为 b,周长为 πb.
因此,这条跑道的周长为 2a + πb.
b
a
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例1
如图,某学校操场最内侧的跑道由两段直道和两段半圆形的弯道组成,其中直道的长为 a,半圆形弯道的直径为 b.
(1)用代数式表示这条跑道的周长;
(2)当a = 67.3 m,b = 52.6 m 时,求这条跑道的周长(π取3.14,结果取整数).
解
(2)当 a = 67.3 m,b = 52.6 m 时,
2a + πb = 2×67.3 + 3.14×52.6
≈ 300(m)
因此,这条跑道的周长约为 300 m.
b
a
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例2
一个三角尺的形状和尺寸如图所示,用代数式表示这个三角尺的面积 S.当 a = 10 cm,b = 17.3 cm,r = 2 cm 时,求这个三角尺的面积(π 取 3.14)
r
a
b
分析:三角尺的面积 = 三角形的面积 - 圆的面积.根据三角形、圆的面积公式可以求出三角尺的面积.
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例2
一个三角尺的形状和尺寸如图所示,用代数式表示这个三角尺的面积 S.当 a = 10 cm,b = 17.3 cm,r = 2 cm 时,求这个三角尺的面积(π 取 3.14)
r
a
b
解
三角形的面积为ab,圆的面积为πr ,S=ab - πr2 .
当a=10 cm,b=17.3 cm,r=2 cm时,
因此,这个三角尺的面积是73.94 cm2.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.如图是一个长为 x,宽为 y 的长方形休闲广场,在它的四角各修建一块半径为 r 的四分之一圆形的花坛(阴影部分),其余部分作为休闲区.
(1)用代数式表示休闲区的面积;
(2)若长方形休闲广场的长为 50 m,宽为 20 m,四分之一圆形花坛的半径为 8 m,求休闲区的面积(π 取3.14,结果取整数).
分析:花坛的面积=4×圆的面积.休闲区的面积 = 长方形休闲广场的面积-花坛的面积.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.如图是一个长为 x,宽为 y 的长方形休闲广场,在它的四角各修建一块半径为 r 的四分之一圆形的花坛(阴影部分),其余部分作为休闲区.
(1)用代数式表示休闲区的面积;
(2)若长方形休闲广场的长为 50 m,宽为 20 m,四分之一圆形花坛的半径为 8 m,求休闲区的面积(π 取3.14,结果取整数).
解:(1)休闲区的面积 S = xy - πr2.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.如图是一个长为 x,宽为 y 的长方形休闲广场,在它的四角各修建一块半径为 r 的四分之一圆形的花坛(阴影部分),其余部分作为休闲区.
(2)若长方形休闲广场的长为 50 m,宽为 20 m,四分之一圆形花坛的半径为 8 m,求休闲区的面积(π 取3.14,结果取整数).
解:(2)当x = 50 m,y = 20 m,r = 8 m 时,
S = xy - πr2 = 50×20 - 3.14×82 ≈ 799 (m2).
因此,休闲区的面积约为 799 m2.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
2.填空题.
(1)若 a,b 分别表示平行四边形的底和高,则面积S =_____;当 a = 2 cm,b = 3 cm 时,S =____cm2.
ab
6
(2)若 a,b 分别表示梯形的上底和下底,h 表示梯形的高,则面积 S =_________;当 a = 2 cm,b = 4 cm,h = 5 cm 时,S =________cm2.
15
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
3.一个长方体纸箱的长是a,宽与高都是b,用代数式表示这个纸箱的体积V.当a=60 cm,b=40 cm时,求这个纸箱的体积.
解:这个纸箱的体积V=a·b·b=a·b2.
当a=60 cm,b=40 cm时,
这个纸箱的体积V=60×40×40=96000.
答:这个纸箱的体积V=a·b2.
当a=60 cm,b=40 cm时,这个纸箱的体积是96000 cm3.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
4.如图,用代数式表示圆环的面积.当 R = 15 cm,r = 10 cm 时,求圆环的面积(π 取 3.14).
解:圆环的面积为 πR2 - πr2 .
当 R = 15 cm,r = 10 cm 时,
πR2 – πr2 = 3.14×152 - 3.14×102 = 392.5 (cm2).
因此,圆环的面积为392.5 cm2 .
对应中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.(2025·湖北·中考真题)一个矩形相邻两边的长分别为2,m,则这个矩形的面积是______.
[答案]2m
[分析]该题考查了列代数式,根据矩形的性质求面积,根据矩形的面积是长×宽即可解答.
[详解]解:根据题意可得矩形的面积是2m,
故答案为:2m.
对应中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
2.(2024·四川雅安·中考真题) 如图是1个纸杯和若干个叠放在一起的纸杯的示意图,在探究纸杯叠放在一起后的总高度H与杯子数量n的变化规律的活动中,我们可以获得以下数据(字母),请选用适当的字母表示______.
①杯子底部到杯沿底边的高h;②杯口直径D;③杯底直径d;④杯沿高a.
[答案]h+an
[分析]本题考查的是列代数式,由总高度=等于杯子底部到杯沿底边的高h加上n个杯子的杯沿高na即可得到答案;
[详解]解:由题意可得:H=h+an,
故答案为:h+an;
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
我亲历了什么
我知道了什么
我会什么
几何中的代数式求值的步骤
求解几何中的代数式求值的应用题
数、形的有效转换
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
几何中的代数式求值的步骤
第一步,利用公式写出代数式
第二步,代入具体数值求值
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
特别提醒
用代数式解决与图形面积有关的问题时,通常将图形分解成几部分,根据它们的构成利用和差关系求解.
对于不能直接求得的图形面积,常运用转化思想将其转化成其他规则图形面积的和或差进行求解.
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
课后作业
A层:P82:习题3.2:第3题,第4题;
B层:P82:习题3.2:第6题,第7题.
下 课
同课章节目录
