2024新人教版八年级上数学 14.2 三角形全等的判定 第4课时 尺规作图问题 课件(共35张PPT)
文档属性
| 名称 | 2024新人教版八年级上数学 14.2 三角形全等的判定 第4课时 尺规作图问题 课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 06:04:05 | ||
图片预览









文档简介
(共35张PPT)
人教版(2024)
八年级上册
14.2 三角形全等的判定
第4课时 尺规作图问题
第十四章·全等三角形
尺规作图问题
知识目标
1.作一个角等于已知角;过直线外一点作这条直线的平行线;已知两边及其夹角、两角及其夹边作三角形;
2.通过实践验证全等三角形的判定定理,明确作图步骤背后的数学依据.
能力目标
1.将抽象的文字描述转化为具体的图形表达,培养从条件出发设计合理作图路径的思维习惯;
2.能够清晰阐述作图依据,并用规范术语书写证明过程,实现“做中学、说中学”.
素质目标
1.体会尺规作图的历史意义,感受数学的美学与理性精神;
2.在小组互助中分享经验技巧,学会倾听他人思路并优化自身方案.
教学难点
教学重点
典型尺规作图的具体步骤
尺规作图的作图顺序
情景导入
1
合作探究
2
抽象概括
3
示范讲解
4
课堂练习
5
课堂小结
6
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
尺规作图的起源
古希腊数学家如欧几里得将尺规作图系统化,他在《几何原本》中详细阐述了尺规作图的基本规则和方法,这些规则成为后世几何学的重要基石,推动了数学的理论化发展。
古埃及人在土地丈量中使用简单的工具,如绳子和木棍,这些实践为尺规作图的初步发展奠定了基础。他们需要精确划分土地,以确保公平分配,这些经验逐渐积累,形成了早期的几何知识。
古希腊的理论奠基
古埃及的测量实践
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
尺规作图的发展历程
三大作图难题的提出
古希腊时期,数学家们提出了三个著名的尺规作图难题:化圆为方、倍立方体和三等分角。这些问题引发了无数数学家的研究,促进了数学理论的深入发展,尽管这些问题最终被证明无法用尺规解决,但其研究过程极大地丰富了数学知识。
中世纪的传播与改进
在中世纪,尺规作图的知识通过阿拉伯世界传播到欧洲。阿拉伯数学家对尺规作图进行了进一步的研究和改进,他们引入了新的作图方法和工具,为文艺复兴时期的数学复兴奠定了基础。
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
复习旧知
圆规
尺规作图的基本工具
直尺
直尺在尺规作图中用于画直线。它没有刻度,只能用来连接两点或延长已知直线。直尺的使用需要精确的操作,以确保所画直线的准确性,这是尺规作图的基础。
圆规用于画圆和弧线。它可以确定圆的半径和圆心,通过圆规可以构造出许多复杂的几何图形。圆规的使用需要掌握一定的技巧,如保持圆规的稳定性,确保所画圆的准确性。
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
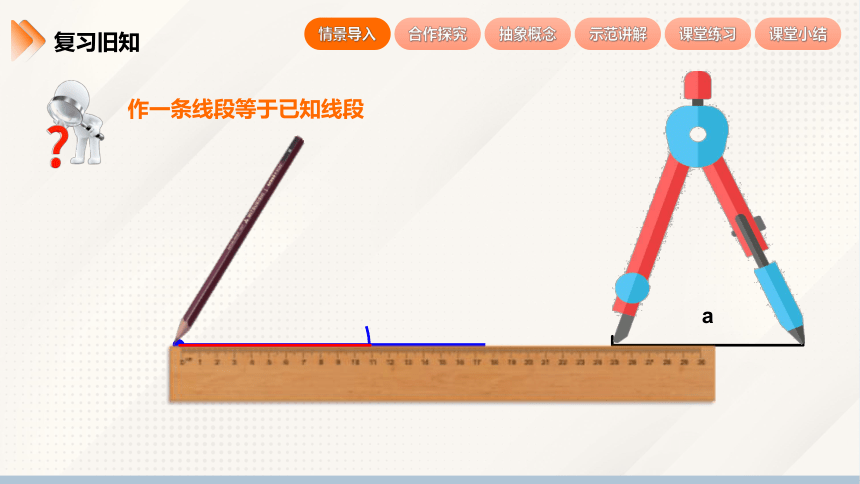
复习旧知
作一条线段等于已知线段
a
尺规作图问题
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
尺规作图
只用直尺(没有刻度)和圆规也可以画出一些图形,这种画图方法被称为尺规作图.
由三角形全等判定可以知道,每一种判定两个三角形全等的条件(_____,_____,_____,_____),都只能作出唯一的三角形.
SSS
SAS
ASA
AAS
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
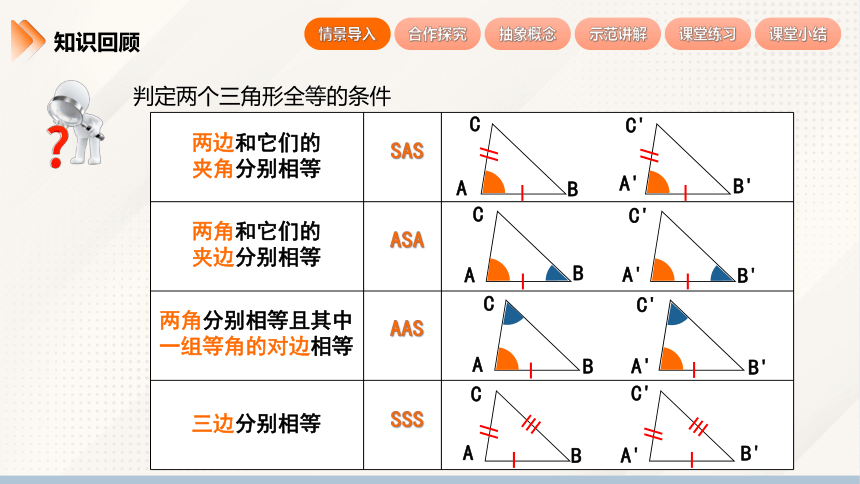
知识回顾
判定两个三角形全等的条件
A
B
C
C'
A'
B'
A
B
C
C'
A'
B'
A
B
C
C'
A'
B'
A
B
C
C'
A'
B'
三边分别相等
两边和它们的
夹角分别相等
两角和它们的
夹边分别相等
两角分别相等且其中
一组等角的对边相等
SSS
SAS
AAS
ASA
分析问题,寻找对应
线段和角都是基本的几何图形,也是构成其他几何图形的元素. 如何用直尺和圆规作一个角等于已知角呢?
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
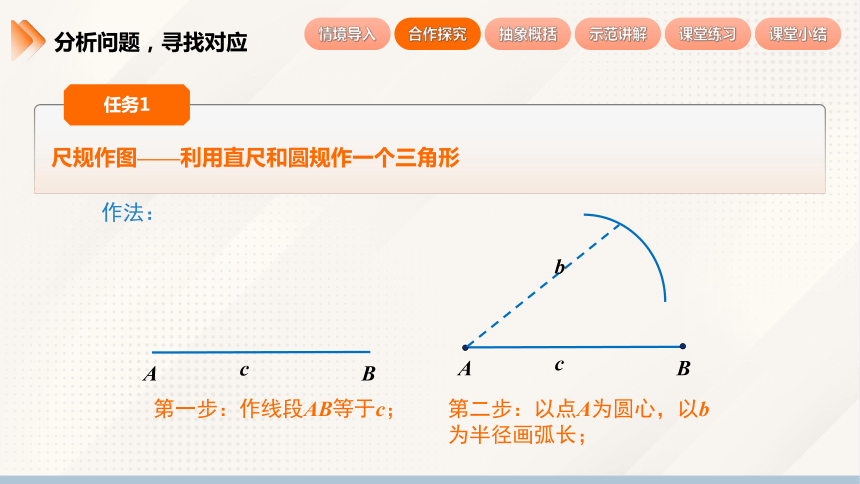
任务1:尺规作图——利用直尺和圆规作一个三角形
已知:已知三条线段 a,b,c(其中任意两条线段的和大于第三条线段),求作△ABC,使其边分别为 a,b,c.
分析问题,寻找对应
尺规作图——利用直尺和圆规作一个三角形
已知:已知三条线段 a,b,c(其中任意两条线段的和大于第三条线段),求作△ABC,使其边分别为 a,b,c.
任务1
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
分析:由作一条线段等于已知线段,能够作出边AB,即A,B两点确定,而BC=a,AC=b,故以点A为圆心,b为半径画弧长,以点B为圆心,a为半径画弧,两弧的交点就是点C.
a
b
c
分析问题,寻找对应
尺规作图——利用直尺和圆规作一个三角形
任务1
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
作法:
第一步:作线段AB等于c;
第二步:以点A为圆心,以b为半径画弧长;
c
B
A
c
B
A
b
分析问题,寻找对应
尺规作图——利用直尺和圆规作一个三角形
任务1
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
作法:
第三步:以点B为圆心,以a为半径画弧,两弧交于点C;
c
B
A
b
a
第四步:连接AC,BC,△ABC即为所求.
c
B
A
b
a
C
分析问题,寻找对应
尺规作图——利用直尺和圆规作一个角等于已知角
已知∠AOB,要用直尺和圆规作一个角与其相等,关键是能用直尺和圆规确定∠AOB 的大小.
任务2
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
分析: 一个三角形的三条边、三个角是确定的. 如果能将∠AOB“放在”某个三角形中,作为其一个角,再作出一个与其全等的三角形,能否得到与∠AOB 一样大小的角?为什么?
O
A
B
能,因为全等三角形的对应角相等.
分析问题,寻找对应
尺规作图——利用直尺和圆规作一个角等于已知角
已知∠AOB,要用直尺和圆规作一个角与其相等,关键是能用直尺和圆规确定∠AOB 的大小.
任务2
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
思考1: 如何围绕∠AOB 构建一个三角形?
O
A
B
如图,在∠AOB 的边 OA,OB 上分别取点 C,D,连接 CD,得到△COD. ∠AOB 就是△ COD 的一个内角.
C
D
为了作图方便,一般取 OC = OD.
分析问题,寻找对应
尺规作图——利用直尺和圆规作一个角等于已知角
已知∠AOB,要用直尺和圆规作一个角与其相等,关键是能用直尺和圆规确定∠AOB 的大小.
任务2
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
思考2:为了作出与△COD 全等的三角形,哪种三角形全等的判定方法可以作为作图依据?
O
A
B
如图,在∠AOB 的边 OA,OB 上分别取点 C,D,连接 CD,得到△COD. ∠AOB 就是△ COD 的一个内角.
C
D
分析问题,寻找对应
尺规作图——利用直尺和圆规作一个角等于已知角
已知∠AOB,要用直尺和圆规作一个角与其相等,关键是能用直尺和圆规确定∠AOB 的大小.
任务2
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
O
A
B
第一步:以点 O 为圆心,任意长为半径作弧,分别交 OA,OB 于点 C,D;
C
D
第二步:作一条射线 O'A',以点 O' 为圆心,OC为半径作弧,交 O'A' 于点 C';
O'
A'
C'
分析问题,寻找对应
尺规作图——利用直尺和圆规作一个角等于已知角
已知∠AOB,要用直尺和圆规作一个角与其相等,关键是能用直尺和圆规确定∠AOB 的大小.
任务2
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
O
A
B
第三步:以点 C' 为圆心,CD 为半径作弧,与上一步作的弧相交于点 D';
C
D
第四步: 过点 D' 作射线 O'B',则∠A'O'B' = ∠AOB.
O'
A'
C'
D'
B'
分析问题,寻找对应
尺规作图——利用直尺和圆规过直线外一点作这条直线的平行线
与“作一条线段等于已知线段”一样,“作一个角等于已知角”也是基本、常用的尺规作图,利用它可以进一步完成其他尺规作图.
任务3
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
回顾:我们学过的判定两直线平行的方法有哪些?
① 同位角相等,两直线平行;
② 内错角相等,两直线平行;
③ 同旁内角互补,两直线平行;
④ 如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
这是尺规作图的依据
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
如图,已知直线 AB 及直线 AB 外一点 C,利用直尺和圆规过点 C 作直线 AB 的平行线 CD.
例1
C
A
B
作法:
(1) 过点 C 作一条直线,与直线 AB 相交于点 E;
C
A
B
E
(2) 在点 C 处作∠CEB 的同位角∠FCD,使∠FCD = ∠CEB;
F
D
(3) 反向延长 CD,得直线 CD,则直线 CD // AB.
解:如图,直线 CD 即所求作直线.
分析问题,寻找对应
尺规作图——利用直尺和圆规已知两边及其夹角作三角形
已知线段 a,b (a>b)和∠α,求作△ABC,使 AB = a,AC = b,∠A =∠α.
任务4
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
a
b
α
先作一个角等于已知角
在作出的角的两边上截取指定长度的边
确定三角形的三个顶点的位置
分析问题,寻找对应
尺规作图——利用直尺和圆规已知两边及其夹角作三角形
已知线段 a,b (a>b)和∠α,求作△ABC,使 AB = a,AC = b,∠A =∠α.
任务4
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
α
A
D
E
第一步,作∠DAE=∠α;
分析问题,寻找对应
尺规作图——利用直尺和圆规已知两边及其夹角作三角形
已知线段 a,b (a>b)和∠α,求作△ABC,使 AB = a,AC = b,∠A =∠α.
任务4
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
D
E
A
D
E
B
C
第二步,在射线 AD 上作 AB = a,在射线 AE 上作 AC = b;
分析问题,寻找对应
尺规作图——利用直尺和圆规已知两边及其夹角作三角形
已知线段 a,b (a>b)和∠α,求作△ABC,使 AB = a,AC = b,∠A =∠α.
任务4
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
D
E
A
D
E
B
C
第三步,连接 BC,则△ABC 就是所求作的三角形.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.如图,用直尺和圆规作一个三角形,使这个三角形的两角分别等于∠α,∠β,这两角的夹边等于线段 a.
a
α
β
A
B
C
解:如图,△ABC 即所求作的三角形.
a
α
β
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
2. 如图,已知∠AOB,以点 O 为圆心,以任意长为半径作弧①,分别交 OA,OB 于点E,F,再以点 E 为圆心,以 EF 长为半径作弧,交弧①于点 D,画射线 OD. 若∠AOB = 28°,则∠BOD 的度数为( )
A. 34° B. 62°
C. 56° D. 124°
C
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
3. 已知△ABC,由尺规作图痕迹可知△ABC≌△ABD,判定这两个三角形全等的理由为( )
A. SSS B. SAS
C. AAS D. ASA
D
对应中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.(2024·北京)下面是“作一个角使其等于∠AOB”的尺规作图方法.
(1)如图,以点O为圆心,任意长为半径画弧,分别交OA,OB于点C,D:
(2)作射线O’A’,以点O为圆心,OC长为半径画弧,交O’A’于点C;以点C’为圆心,CD长为
半径画弧,两弧交于点D’;
(3)过点D’作射线O’B’,则∠A’O’B’= ㄥAOB
上述通过判定ΔC’O’D’≌ΔCOD得到∠A’O’B’= ∠AOB,其中判定ΔC’O’D’≌COD的依据是( )
A.三边分别相等的两个三角形全等 B.两边及其夹角分别相等的两个三角形全等
C.两角及其夹边分别相等的两个三角形全等
D.两角分别相等且其中一组等角的对边相等的两个三角形全等
A
对应中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
2.(2024·山东德州)已知∠AOB,点P为OA上一点,用尺规作图,过点P作OB的平行线,下列作图痕迹不正确的是( )
A B
C D
B
对应中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
3.(2024·江苏扬州)如图,已知∠PAQ及AP边上一点C.
用无刻度直尺和圆规在射线AQ上求作点O,使得∠COQ=2∠CAQ;(保留作图痕迹,不写作法)
解:如图所示
∴∠COQ=2∠CAQ;
点0即为所求
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
我亲历了什么
我知道了什么
我会什么
尺规作图的几种情况
独立完成尺规作图要求
明确尺规作图的依据
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
尺规作图
只用直尺(没有刻度)和圆规也可以画出一些图形,这种画图方法被称为尺规作图.
由三角形全等判定可以知道,每一种判定两个三角形全等的条件(_____,_____,_____,_____),都只能作出唯一的三角形.
SSS
SAS
ASA
AAS
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
尺规作图
依据:SSS
依据:“同位角相等,两直线平行”或“内错角相等,两直线平行”
作一个角等于已知角
过直线外一点作这条直线的平行线
已知两边及其夹角作三角形,已知两角及其夹边作三角形.
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
课后作业
A层:P44:习题14.2:9题.
B层:P44:习题14.2:10题.
下 课
人教版(2024)
八年级上册
14.2 三角形全等的判定
第4课时 尺规作图问题
第十四章·全等三角形
尺规作图问题
知识目标
1.作一个角等于已知角;过直线外一点作这条直线的平行线;已知两边及其夹角、两角及其夹边作三角形;
2.通过实践验证全等三角形的判定定理,明确作图步骤背后的数学依据.
能力目标
1.将抽象的文字描述转化为具体的图形表达,培养从条件出发设计合理作图路径的思维习惯;
2.能够清晰阐述作图依据,并用规范术语书写证明过程,实现“做中学、说中学”.
素质目标
1.体会尺规作图的历史意义,感受数学的美学与理性精神;
2.在小组互助中分享经验技巧,学会倾听他人思路并优化自身方案.
教学难点
教学重点
典型尺规作图的具体步骤
尺规作图的作图顺序
情景导入
1
合作探究
2
抽象概括
3
示范讲解
4
课堂练习
5
课堂小结
6
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
尺规作图的起源
古希腊数学家如欧几里得将尺规作图系统化,他在《几何原本》中详细阐述了尺规作图的基本规则和方法,这些规则成为后世几何学的重要基石,推动了数学的理论化发展。
古埃及人在土地丈量中使用简单的工具,如绳子和木棍,这些实践为尺规作图的初步发展奠定了基础。他们需要精确划分土地,以确保公平分配,这些经验逐渐积累,形成了早期的几何知识。
古希腊的理论奠基
古埃及的测量实践
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
尺规作图的发展历程
三大作图难题的提出
古希腊时期,数学家们提出了三个著名的尺规作图难题:化圆为方、倍立方体和三等分角。这些问题引发了无数数学家的研究,促进了数学理论的深入发展,尽管这些问题最终被证明无法用尺规解决,但其研究过程极大地丰富了数学知识。
中世纪的传播与改进
在中世纪,尺规作图的知识通过阿拉伯世界传播到欧洲。阿拉伯数学家对尺规作图进行了进一步的研究和改进,他们引入了新的作图方法和工具,为文艺复兴时期的数学复兴奠定了基础。
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
复习旧知
圆规
尺规作图的基本工具
直尺
直尺在尺规作图中用于画直线。它没有刻度,只能用来连接两点或延长已知直线。直尺的使用需要精确的操作,以确保所画直线的准确性,这是尺规作图的基础。
圆规用于画圆和弧线。它可以确定圆的半径和圆心,通过圆规可以构造出许多复杂的几何图形。圆规的使用需要掌握一定的技巧,如保持圆规的稳定性,确保所画圆的准确性。
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
复习旧知
作一条线段等于已知线段
a
尺规作图问题
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
尺规作图
只用直尺(没有刻度)和圆规也可以画出一些图形,这种画图方法被称为尺规作图.
由三角形全等判定可以知道,每一种判定两个三角形全等的条件(_____,_____,_____,_____),都只能作出唯一的三角形.
SSS
SAS
ASA
AAS
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
知识回顾
判定两个三角形全等的条件
A
B
C
C'
A'
B'
A
B
C
C'
A'
B'
A
B
C
C'
A'
B'
A
B
C
C'
A'
B'
三边分别相等
两边和它们的
夹角分别相等
两角和它们的
夹边分别相等
两角分别相等且其中
一组等角的对边相等
SSS
SAS
AAS
ASA
分析问题,寻找对应
线段和角都是基本的几何图形,也是构成其他几何图形的元素. 如何用直尺和圆规作一个角等于已知角呢?
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
任务1:尺规作图——利用直尺和圆规作一个三角形
已知:已知三条线段 a,b,c(其中任意两条线段的和大于第三条线段),求作△ABC,使其边分别为 a,b,c.
分析问题,寻找对应
尺规作图——利用直尺和圆规作一个三角形
已知:已知三条线段 a,b,c(其中任意两条线段的和大于第三条线段),求作△ABC,使其边分别为 a,b,c.
任务1
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
分析:由作一条线段等于已知线段,能够作出边AB,即A,B两点确定,而BC=a,AC=b,故以点A为圆心,b为半径画弧长,以点B为圆心,a为半径画弧,两弧的交点就是点C.
a
b
c
分析问题,寻找对应
尺规作图——利用直尺和圆规作一个三角形
任务1
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
作法:
第一步:作线段AB等于c;
第二步:以点A为圆心,以b为半径画弧长;
c
B
A
c
B
A
b
分析问题,寻找对应
尺规作图——利用直尺和圆规作一个三角形
任务1
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
作法:
第三步:以点B为圆心,以a为半径画弧,两弧交于点C;
c
B
A
b
a
第四步:连接AC,BC,△ABC即为所求.
c
B
A
b
a
C
分析问题,寻找对应
尺规作图——利用直尺和圆规作一个角等于已知角
已知∠AOB,要用直尺和圆规作一个角与其相等,关键是能用直尺和圆规确定∠AOB 的大小.
任务2
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
分析: 一个三角形的三条边、三个角是确定的. 如果能将∠AOB“放在”某个三角形中,作为其一个角,再作出一个与其全等的三角形,能否得到与∠AOB 一样大小的角?为什么?
O
A
B
能,因为全等三角形的对应角相等.
分析问题,寻找对应
尺规作图——利用直尺和圆规作一个角等于已知角
已知∠AOB,要用直尺和圆规作一个角与其相等,关键是能用直尺和圆规确定∠AOB 的大小.
任务2
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
思考1: 如何围绕∠AOB 构建一个三角形?
O
A
B
如图,在∠AOB 的边 OA,OB 上分别取点 C,D,连接 CD,得到△COD. ∠AOB 就是△ COD 的一个内角.
C
D
为了作图方便,一般取 OC = OD.
分析问题,寻找对应
尺规作图——利用直尺和圆规作一个角等于已知角
已知∠AOB,要用直尺和圆规作一个角与其相等,关键是能用直尺和圆规确定∠AOB 的大小.
任务2
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
思考2:为了作出与△COD 全等的三角形,哪种三角形全等的判定方法可以作为作图依据?
O
A
B
如图,在∠AOB 的边 OA,OB 上分别取点 C,D,连接 CD,得到△COD. ∠AOB 就是△ COD 的一个内角.
C
D
分析问题,寻找对应
尺规作图——利用直尺和圆规作一个角等于已知角
已知∠AOB,要用直尺和圆规作一个角与其相等,关键是能用直尺和圆规确定∠AOB 的大小.
任务2
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
O
A
B
第一步:以点 O 为圆心,任意长为半径作弧,分别交 OA,OB 于点 C,D;
C
D
第二步:作一条射线 O'A',以点 O' 为圆心,OC为半径作弧,交 O'A' 于点 C';
O'
A'
C'
分析问题,寻找对应
尺规作图——利用直尺和圆规作一个角等于已知角
已知∠AOB,要用直尺和圆规作一个角与其相等,关键是能用直尺和圆规确定∠AOB 的大小.
任务2
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
O
A
B
第三步:以点 C' 为圆心,CD 为半径作弧,与上一步作的弧相交于点 D';
C
D
第四步: 过点 D' 作射线 O'B',则∠A'O'B' = ∠AOB.
O'
A'
C'
D'
B'
分析问题,寻找对应
尺规作图——利用直尺和圆规过直线外一点作这条直线的平行线
与“作一条线段等于已知线段”一样,“作一个角等于已知角”也是基本、常用的尺规作图,利用它可以进一步完成其他尺规作图.
任务3
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
回顾:我们学过的判定两直线平行的方法有哪些?
① 同位角相等,两直线平行;
② 内错角相等,两直线平行;
③ 同旁内角互补,两直线平行;
④ 如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
这是尺规作图的依据
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
如图,已知直线 AB 及直线 AB 外一点 C,利用直尺和圆规过点 C 作直线 AB 的平行线 CD.
例1
C
A
B
作法:
(1) 过点 C 作一条直线,与直线 AB 相交于点 E;
C
A
B
E
(2) 在点 C 处作∠CEB 的同位角∠FCD,使∠FCD = ∠CEB;
F
D
(3) 反向延长 CD,得直线 CD,则直线 CD // AB.
解:如图,直线 CD 即所求作直线.
分析问题,寻找对应
尺规作图——利用直尺和圆规已知两边及其夹角作三角形
已知线段 a,b (a>b)和∠α,求作△ABC,使 AB = a,AC = b,∠A =∠α.
任务4
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
a
b
α
先作一个角等于已知角
在作出的角的两边上截取指定长度的边
确定三角形的三个顶点的位置
分析问题,寻找对应
尺规作图——利用直尺和圆规已知两边及其夹角作三角形
已知线段 a,b (a>b)和∠α,求作△ABC,使 AB = a,AC = b,∠A =∠α.
任务4
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
α
A
D
E
第一步,作∠DAE=∠α;
分析问题,寻找对应
尺规作图——利用直尺和圆规已知两边及其夹角作三角形
已知线段 a,b (a>b)和∠α,求作△ABC,使 AB = a,AC = b,∠A =∠α.
任务4
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
D
E
A
D
E
B
C
第二步,在射线 AD 上作 AB = a,在射线 AE 上作 AC = b;
分析问题,寻找对应
尺规作图——利用直尺和圆规已知两边及其夹角作三角形
已知线段 a,b (a>b)和∠α,求作△ABC,使 AB = a,AC = b,∠A =∠α.
任务4
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
D
E
A
D
E
B
C
第三步,连接 BC,则△ABC 就是所求作的三角形.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.如图,用直尺和圆规作一个三角形,使这个三角形的两角分别等于∠α,∠β,这两角的夹边等于线段 a.
a
α
β
A
B
C
解:如图,△ABC 即所求作的三角形.
a
α
β
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
2. 如图,已知∠AOB,以点 O 为圆心,以任意长为半径作弧①,分别交 OA,OB 于点E,F,再以点 E 为圆心,以 EF 长为半径作弧,交弧①于点 D,画射线 OD. 若∠AOB = 28°,则∠BOD 的度数为( )
A. 34° B. 62°
C. 56° D. 124°
C
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
3. 已知△ABC,由尺规作图痕迹可知△ABC≌△ABD,判定这两个三角形全等的理由为( )
A. SSS B. SAS
C. AAS D. ASA
D
对应中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.(2024·北京)下面是“作一个角使其等于∠AOB”的尺规作图方法.
(1)如图,以点O为圆心,任意长为半径画弧,分别交OA,OB于点C,D:
(2)作射线O’A’,以点O为圆心,OC长为半径画弧,交O’A’于点C;以点C’为圆心,CD长为
半径画弧,两弧交于点D’;
(3)过点D’作射线O’B’,则∠A’O’B’= ㄥAOB
上述通过判定ΔC’O’D’≌ΔCOD得到∠A’O’B’= ∠AOB,其中判定ΔC’O’D’≌COD的依据是( )
A.三边分别相等的两个三角形全等 B.两边及其夹角分别相等的两个三角形全等
C.两角及其夹边分别相等的两个三角形全等
D.两角分别相等且其中一组等角的对边相等的两个三角形全等
A
对应中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
2.(2024·山东德州)已知∠AOB,点P为OA上一点,用尺规作图,过点P作OB的平行线,下列作图痕迹不正确的是( )
A B
C D
B
对应中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
3.(2024·江苏扬州)如图,已知∠PAQ及AP边上一点C.
用无刻度直尺和圆规在射线AQ上求作点O,使得∠COQ=2∠CAQ;(保留作图痕迹,不写作法)
解:如图所示
∴∠COQ=2∠CAQ;
点0即为所求
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
我亲历了什么
我知道了什么
我会什么
尺规作图的几种情况
独立完成尺规作图要求
明确尺规作图的依据
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
尺规作图
只用直尺(没有刻度)和圆规也可以画出一些图形,这种画图方法被称为尺规作图.
由三角形全等判定可以知道,每一种判定两个三角形全等的条件(_____,_____,_____,_____),都只能作出唯一的三角形.
SSS
SAS
ASA
AAS
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
尺规作图
依据:SSS
依据:“同位角相等,两直线平行”或“内错角相等,两直线平行”
作一个角等于已知角
过直线外一点作这条直线的平行线
已知两边及其夹角作三角形,已知两角及其夹边作三角形.
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
课后作业
A层:P44:习题14.2:9题.
B层:P44:习题14.2:10题.
下 课
同课章节目录
