2024新人教版八年级上数学 14.2 三角形全等的判定 第5课时 用 ''HL'' 判定直角三角形全等 课件(共35张PPT)
文档属性
| 名称 | 2024新人教版八年级上数学 14.2 三角形全等的判定 第5课时 用 ''HL'' 判定直角三角形全等 课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 06:03:38 | ||
图片预览






文档简介
(共35张PPT)
人教版(2024)
八年级上册
14.2 三角形全等的判定
第5课时 用 ''HL''
判定直角三角形全等
第十四章·全等三角形
判定直角三角形全等
知识目标
1.理解并掌握“HL”定理的内容。
2.明确该定理适用于仅当其中一个角为90°的特殊情形,区分其与一般三角形全等判定条件的不同。
3.能够准确识别题目中的已知条件是否符合HL定理的应用前提。
能力目标
1.用规范的数学语言书写证明步骤,能基于HL定理进行简单的几何论证。
2.在复杂图形中提取关键信息,灵活运用HL定理解决实际问题。
素质目标
1.渗透“特殊与一般”“分类讨论”的辩证思维思想,体会数学定理的严谨性和普适性。
2.培养科学探究精神,鼓励学生通过猜想—验证—结论的研究路径自主建构知识。
教学难点
教学重点
HL定理的条件与结论
“必须包含斜边”是关键前提,例如仅知两条直角边相等时不能用HL
情景导入
1
合作探究
2
抽象概括
3
示范讲解
4
课堂练习
5
课堂小结
6
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
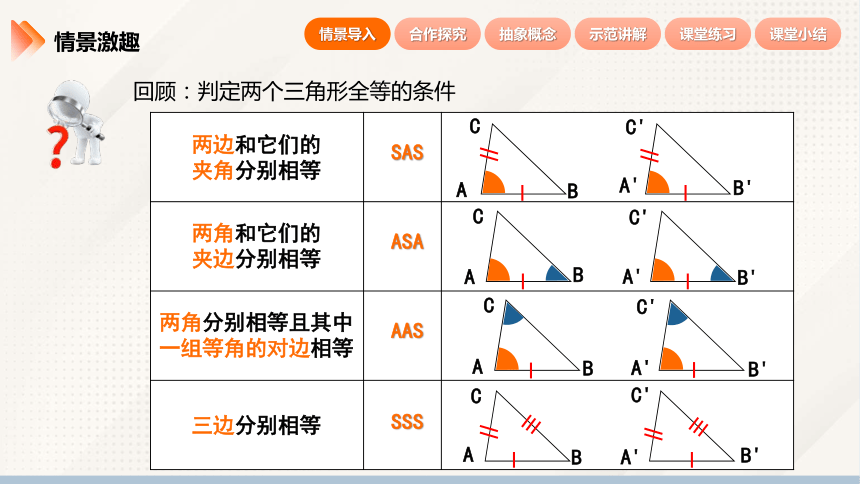
回顾:判定两个三角形全等的条件
A
B
C
C'
A'
B'
A
B
C
C'
A'
B'
A
B
C
C'
A'
B'
A
B
C
C'
A'
B'
三边分别相等
两边和它们的
夹角分别相等
两角和它们的
夹边分别相等
两角分别相等且其中
一组等角的对边相等
SSS
SAS
AAS
ASA
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
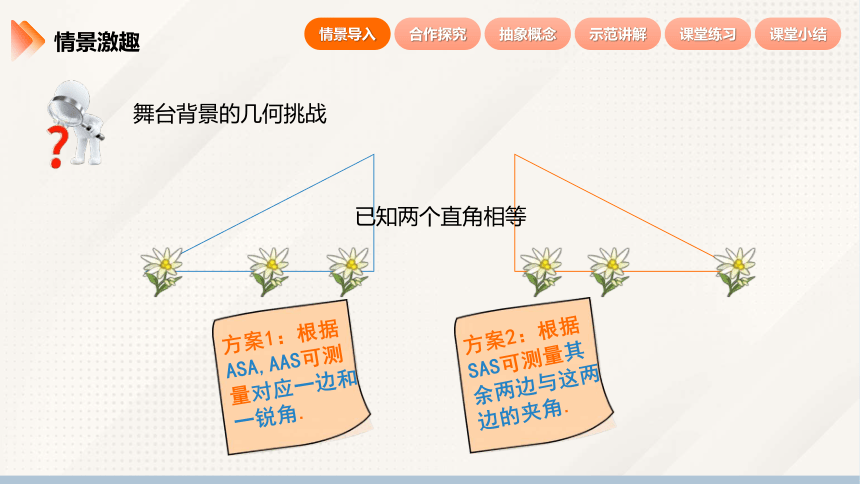
舞台背景的几何挑战
如图,舞台背景的形状是两个直角三角形, 为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.你能帮工作人员想个办法吗?
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
舞台背景的几何挑战
方案2:根据SAS可测量其余两边与这两边的夹角.
方案1:根据ASA,AAS可测量对应一边和一锐角.
已知两个直角相等
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠B和∠F的大小有什么关系?
探究判定两个直角三角形全等的条件
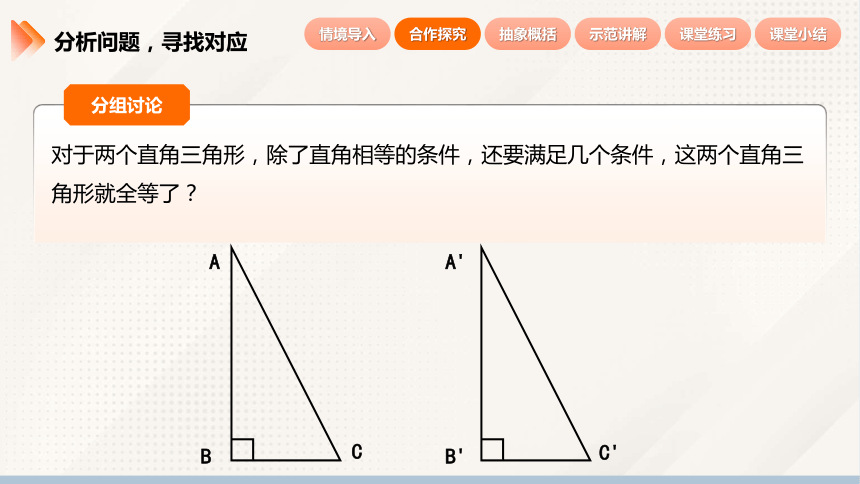
分析问题,寻找对应
对于两个直角三角形,除了直角相等的条件,还要满足几个条件,这两个直角三角形就全等了?
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
B
C
A'
B'
C'
分析问题,寻找对应
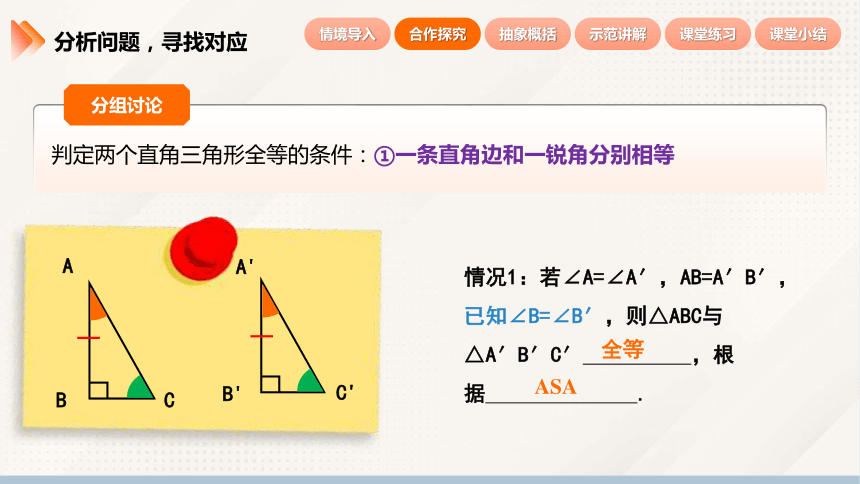
判定两个直角三角形全等的条件:①一条直角边和一锐角分别相等
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
B
C
A'
B'
C'
情况1:若∠A=∠A′,AB=A′B′,已知∠B=∠B′,则△ABC与△A′B′C′ ,根据 .
ASA
全等
分析问题,寻找对应
判定两个直角三角形全等的条件:①一条直角边和一锐角分别相等
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
B
C
A'
B'
C'
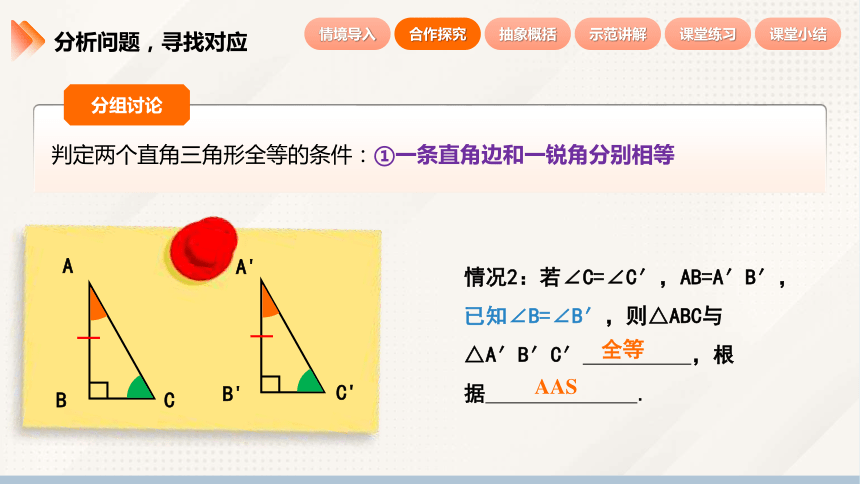
AAS
情况2:若∠C=∠C′,AB=A′B′,已知∠B=∠B′,则△ABC与△A′B′C′ ,根据 .
全等
分析问题,寻找对应
判定两个直角三角形全等的条件:②斜边和一锐角分别相等
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
B
C
A'
B'
C'
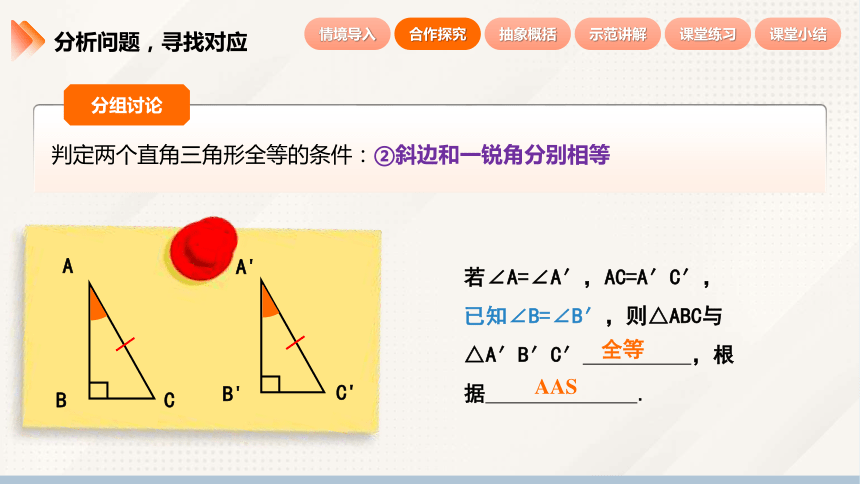
若∠A=∠A′,AC=A′C′,
已知∠B=∠B′,则△ABC与△A′B′C′ ,根据 .
AAS
全等
分析问题,寻找对应
判定两个直角三角形全等的条件:③两直角边分别相等
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
B
C
A'
B'
C'
若AB=A′B′,BC=B′C′,
已知∠B=∠B′,则△ABC与△A′B′C′ ,根据 .
ASA
全等
分析问题,寻找对应
如果满足斜边和一条直角边分别相等呢?能证明全等吗?
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
分析问题,寻找对应
任意画一个Rt△ABC,使∠C =90°,再画一个Rt△A′B′C′,使∠C′=90°,B′C′=BC,A′B′=AB,然后把画好的Rt△A′B′C′剪下来放到Rt△ABC上,你发现了什么?
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
B
C
作法:
(1)画∠MC'N=90°;
(2)在射线C'M上截取B'C'=BC;
(3)以点B'为圆心,AB为半径画弧,交射线C'N于点A';
(4)连接A'B'.
分析问题,寻找对应
任意画一个Rt△ABC,使∠C =90°,再画一个Rt△A′B′C′,使∠C′=90°,B′C′=BC,A′B′=AB,然后把画好的Rt△A′B′C′剪下来放到Rt△ABC上,你发现了什么?
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
C ′
N
M
A
B
C
A ′
B ′
两个三角形放在一起能完全重合
分析问题,寻找对应
接下来讨论射线 CA 上除点 C,A 外的点与点 B 的连线和边 AB 的大小关系.
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
C
A
B
(C')
(B')
① 设点 M 在直角边 AC (不包括端点)上,连接 BM,则∠BMA >∠C,∠BMA是钝角.
② 若过点 M 且垂直于 BM 的直线与线段 AB 相交于点 M′,则有 AB > BM′ > BM.
M
外角的性质
M'
垂线段最短
分析问题,寻找对应
接下来讨论射线 CA 上除点 C,A 外的点与点 B 的连线和边 AB 的大小关系.
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
C
A
B
(C')
(B')
③ 设点 N 在线段 CA 的延长线上,连接 BN,同理可得 BN > AB.
④ 因此,在射线 CA 上,与点 B 的连线长度等于 AB 的点只有一个.
M
M'
在点 A 下方时,长度 < AB;在点 A 上方时,长度 > AB.
N
⑤再由点 A′ 在射线 CA 上,
A′B′ = AB,可知点 A′与点 A 重合.
判定直角三角形全等
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
斜边和一直角边分别相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”)
如图,在Rt△ABC 与 Rt△A′B′C′ 中,
∴Rt△ABC≌Rt△A′B′C′ (HL)
AB =A′B′
BC = B′C′
几何语言:
基本事实:
知识点 用“HL”判定直角三角形全等
C
A
B
C'
A'
B'
判定直角三角形全等
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
在使用“HL”时,同学们应注意什么
(1)“HL”是仅适用于直角三角形的特殊方法.
两个“△”前要加“Rt”.
(2)注意对应相等.
”HL”中“H”代表斜边,“L”代表直角边.
“斜边-直角边”顺序不要混淆.
在Rt△ABC 与 Rt△A′B′C′ 中,
∴Rt△ABC≌Rt△A′B′C′ (HL)
AB =A′B′
BC = B′C′
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例1
解
证明:∵ AC⊥BC,BD⊥AD,
∴ ∠C =∠D = 90°.
在Rt△ABC 和 Rt△BAD 中,
AB = BA,
AC = BD,
∴ Rt△ABC ≌ Rt△BAD(HL).
∴ BC =AD(全等三角形对应边相等).
如图,AC⊥BC,BD⊥AD,垂足分别为C,D,AC = BD.
求证 BC =AD.
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例2
如图,AC⊥BC,BD⊥AD,要明证△ABC ≌△BAD,需要添加一个什么条件?请说明理由.
(1) ( );
(2) ( );
(3) ( );
(4) ( ).
AD = BC
AC = BD
∠DAB = ∠CBA
∠DBA = ∠CAB
HL
HL
AAS
AAS
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例3
如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠B和∠F的大小有什么关系?
解
在Rt△ABC和Rt△DEF中,
BC=EF,
AC=DF ,
∴ Rt△ABC≌Rt△DEF (HL).
∴∠B=∠DEF.
∵ ∠DEF+∠F=90°,
∴∠B+∠F=90°.
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例4
如图,两根长度均为12m的绳子,一端系在旗杆上,另一端分别固定在地面的两个木桩上,两个木桩离旗杆底部的距离相等吗 请说明你的理由.
解
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在Rt△ABD和Rt △ACD中,
∴Rt△ABD≌Rt △ACD(HL),
∴BD=CD.
AB=AC,
∠ADB=∠ADC ,
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.如图,C 是路段AB 的中点,两人从C 同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地.DA⊥AB,EB⊥AB. D,E 与路段AB的距离相等吗?为什么?
A
B
C
D
E
分析:CA=CB
CD=CE
∠A=∠B=90°
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.如图,C 是路段AB 的中点,两人从C 同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地.DA⊥AB,EB⊥AB. D,E 与路段AB的距离相等吗?为什么?
A
B
C
D
E
解:D,E与线段AB的距离相等.
∵C是路段AB的中点,
∴AC=BC.
∵DA⊥AB , EB⊥AB ,
∴∠A=∠B=90°.
CD=CE,
AC=CB,
在Rt△ADC 和Rt△BEC 中,
∴ Rt△ADC ≌ Rt△BEC (HL).
∴ AD =BE.
∴ D,E与线段AB的距离相等.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
2.如图,AB =CD,AE⊥BC,DF⊥BC,垂足分别为E ,F,CE =BF.求证:(1)AE =DF ; (2)CD//AB.
A
B
C
D
E
F
分析: CE-EF=BF-EF,即CF=BE
Rt△ABE ≌ Rt△DCF(HL)
AE=DF
∠B=∠C
CD//AB
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
2.如图,AB =CD,AE⊥BC,DF⊥BC,垂足分别为E ,F,CE =BF.求证:(1)AE =DF ; (2)CD//AB.
A
B
C
D
E
F
证明:∵CE=BF,
∵AE⊥BC , DF⊥BC ,
∴∠AEB=∠DFC=90°.
AB=DC,
CF=BE,
在Rt△ABE 和Rt△DCF 中,
∴ Rt△ABE ≌ Rt△DCF (HL).
∴ AE=DF , ∠B=∠C.
∴ CD//AB.
∴CE-EF=BF-EF,即CF=BE.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
3.如图,已知AB=AC,AE=AF, AE⊥EC,AF⊥BF,
垂足分别是点E、F.求证:∠1=∠2.
A
B
C
E
F
1
2
证明:∵ AE⊥EC,AF⊥BF ,
∴∠E=∠F=90°.
在Rt△AEC 和 Rt△AFB 中,
AC =AB,
AE =AF,
∴Rt△AEC ≌ Rt△AFB(HL).
∴∠EAC=∠FAB.
∴∠EAC-∠BAC=∠FAB-∠BAC.
∴∠1=∠2.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
4.如图 在△ABC中,已知BD⊥AC,CE ⊥AB,BD=CE.求证:△EBC≌△DCB.
A
B
C
E
D
证明:∵ BD⊥AC,CE⊥AB,
∴∠BEC=∠BDC=90 °.
在 Rt△EBC 和Rt△DCB 中,
CE=BD,
BC=CB .
∴ Rt△EBC≌Rt△DCB (HL).
对应中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.(2025·重庆)学习了角平分线和尺规作图后,小红进行了拓展性研究,她发现了角平分线的另一种作法,并与她的同伴进行交流,现在你作为她的同伴,请根据她的想法与思路,完成以下作图和填空:
第一步:构造角平分线.
小红在∠AOB的边OA上任取一点E,并过点E作了OA的垂线(如图).请你利用尺规作图,在OB边上截取OF=OE,过点F作OB的垂线与小红所作的垂线交于点P,作射线OP,OP即为∠AOB的平分线(不写作法,保留作图痕迹).
第二步:利用三角形全等证明她的猜想.
证明:∵PE⊥OA,PF⊥OB,
∴∠OEP=∠OFP=90°.
在RtΔOEP和RtΔOFP中,
① ,
② ,
∴ Rt ΔOEP≌Rt ΔOFP(HL)
∴ ③ .
∴OP平分∠AOB
①PO=PO; ②OE=OF;③∠EOP= ∠FOP
对应中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
2.(2023·浙江)如图,在RtΔABC中,∠ACB=90°,0为AC边上一点,连结OB,以OC为半径的半圆与AB边相切于点D,交AC边于点E.
求证:BC=BD.
证明:如图,连接OD,
∵BD是⊙O的切线,点D为切点,
∴∠ODB=90°,
∠ACB=90°,
∴RtΔODB≌RtΔOCB(HL).
∴BC=BD.
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
我亲历了什么
我知道了什么
我会什么
用“HL”判定直角三角形全等
独立书写用“HL”判定直角三角形全等的步骤
推导判定两个直角三角形全等的条件
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
斜边和一直角边分别相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”)
基本事实:
知识点 用“HL”判定直角三角形全等
(1)“HL”是仅适用于直角三角形的特殊方法.
两个“△”前要加“Rt”.
(2)注意对应相等.
”HL”中“H”代表斜边,“L”代表直角边.
“斜边-直角边”顺序不要混淆.
在Rt△ABC 与 Rt△A′B′C′ 中,
∴Rt△ABC≌Rt△A′B′C′ (HL)
AB =A′B′
BC = B′C′
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
课后作业
A层:P43:习题14.2:11题.
B层:P43:习题14.2:12题.
下 课
人教版(2024)
八年级上册
14.2 三角形全等的判定
第5课时 用 ''HL''
判定直角三角形全等
第十四章·全等三角形
判定直角三角形全等
知识目标
1.理解并掌握“HL”定理的内容。
2.明确该定理适用于仅当其中一个角为90°的特殊情形,区分其与一般三角形全等判定条件的不同。
3.能够准确识别题目中的已知条件是否符合HL定理的应用前提。
能力目标
1.用规范的数学语言书写证明步骤,能基于HL定理进行简单的几何论证。
2.在复杂图形中提取关键信息,灵活运用HL定理解决实际问题。
素质目标
1.渗透“特殊与一般”“分类讨论”的辩证思维思想,体会数学定理的严谨性和普适性。
2.培养科学探究精神,鼓励学生通过猜想—验证—结论的研究路径自主建构知识。
教学难点
教学重点
HL定理的条件与结论
“必须包含斜边”是关键前提,例如仅知两条直角边相等时不能用HL
情景导入
1
合作探究
2
抽象概括
3
示范讲解
4
课堂练习
5
课堂小结
6
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
回顾:判定两个三角形全等的条件
A
B
C
C'
A'
B'
A
B
C
C'
A'
B'
A
B
C
C'
A'
B'
A
B
C
C'
A'
B'
三边分别相等
两边和它们的
夹角分别相等
两角和它们的
夹边分别相等
两角分别相等且其中
一组等角的对边相等
SSS
SAS
AAS
ASA
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
舞台背景的几何挑战
如图,舞台背景的形状是两个直角三角形, 为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量.你能帮工作人员想个办法吗?
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
舞台背景的几何挑战
方案2:根据SAS可测量其余两边与这两边的夹角.
方案1:根据ASA,AAS可测量对应一边和一锐角.
已知两个直角相等
情景导入
合作探究
抽象概念
示范讲解
课堂练习
课堂小结
情景激趣
如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠B和∠F的大小有什么关系?
探究判定两个直角三角形全等的条件
分析问题,寻找对应
对于两个直角三角形,除了直角相等的条件,还要满足几个条件,这两个直角三角形就全等了?
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
B
C
A'
B'
C'
分析问题,寻找对应
判定两个直角三角形全等的条件:①一条直角边和一锐角分别相等
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
B
C
A'
B'
C'
情况1:若∠A=∠A′,AB=A′B′,已知∠B=∠B′,则△ABC与△A′B′C′ ,根据 .
ASA
全等
分析问题,寻找对应
判定两个直角三角形全等的条件:①一条直角边和一锐角分别相等
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
B
C
A'
B'
C'
AAS
情况2:若∠C=∠C′,AB=A′B′,已知∠B=∠B′,则△ABC与△A′B′C′ ,根据 .
全等
分析问题,寻找对应
判定两个直角三角形全等的条件:②斜边和一锐角分别相等
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
B
C
A'
B'
C'
若∠A=∠A′,AC=A′C′,
已知∠B=∠B′,则△ABC与△A′B′C′ ,根据 .
AAS
全等
分析问题,寻找对应
判定两个直角三角形全等的条件:③两直角边分别相等
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
B
C
A'
B'
C'
若AB=A′B′,BC=B′C′,
已知∠B=∠B′,则△ABC与△A′B′C′ ,根据 .
ASA
全等
分析问题,寻找对应
如果满足斜边和一条直角边分别相等呢?能证明全等吗?
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
分析问题,寻找对应
任意画一个Rt△ABC,使∠C =90°,再画一个Rt△A′B′C′,使∠C′=90°,B′C′=BC,A′B′=AB,然后把画好的Rt△A′B′C′剪下来放到Rt△ABC上,你发现了什么?
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
A
B
C
作法:
(1)画∠MC'N=90°;
(2)在射线C'M上截取B'C'=BC;
(3)以点B'为圆心,AB为半径画弧,交射线C'N于点A';
(4)连接A'B'.
分析问题,寻找对应
任意画一个Rt△ABC,使∠C =90°,再画一个Rt△A′B′C′,使∠C′=90°,B′C′=BC,A′B′=AB,然后把画好的Rt△A′B′C′剪下来放到Rt△ABC上,你发现了什么?
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
C ′
N
M
A
B
C
A ′
B ′
两个三角形放在一起能完全重合
分析问题,寻找对应
接下来讨论射线 CA 上除点 C,A 外的点与点 B 的连线和边 AB 的大小关系.
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
C
A
B
(C')
(B')
① 设点 M 在直角边 AC (不包括端点)上,连接 BM,则∠BMA >∠C,∠BMA是钝角.
② 若过点 M 且垂直于 BM 的直线与线段 AB 相交于点 M′,则有 AB > BM′ > BM.
M
外角的性质
M'
垂线段最短
分析问题,寻找对应
接下来讨论射线 CA 上除点 C,A 外的点与点 B 的连线和边 AB 的大小关系.
分组讨论
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
C
A
B
(C')
(B')
③ 设点 N 在线段 CA 的延长线上,连接 BN,同理可得 BN > AB.
④ 因此,在射线 CA 上,与点 B 的连线长度等于 AB 的点只有一个.
M
M'
在点 A 下方时,长度 < AB;在点 A 上方时,长度 > AB.
N
⑤再由点 A′ 在射线 CA 上,
A′B′ = AB,可知点 A′与点 A 重合.
判定直角三角形全等
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
斜边和一直角边分别相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”)
如图,在Rt△ABC 与 Rt△A′B′C′ 中,
∴Rt△ABC≌Rt△A′B′C′ (HL)
AB =A′B′
BC = B′C′
几何语言:
基本事实:
知识点 用“HL”判定直角三角形全等
C
A
B
C'
A'
B'
判定直角三角形全等
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
在使用“HL”时,同学们应注意什么
(1)“HL”是仅适用于直角三角形的特殊方法.
两个“△”前要加“Rt”.
(2)注意对应相等.
”HL”中“H”代表斜边,“L”代表直角边.
“斜边-直角边”顺序不要混淆.
在Rt△ABC 与 Rt△A′B′C′ 中,
∴Rt△ABC≌Rt△A′B′C′ (HL)
AB =A′B′
BC = B′C′
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例1
解
证明:∵ AC⊥BC,BD⊥AD,
∴ ∠C =∠D = 90°.
在Rt△ABC 和 Rt△BAD 中,
AB = BA,
AC = BD,
∴ Rt△ABC ≌ Rt△BAD(HL).
∴ BC =AD(全等三角形对应边相等).
如图,AC⊥BC,BD⊥AD,垂足分别为C,D,AC = BD.
求证 BC =AD.
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例2
如图,AC⊥BC,BD⊥AD,要明证△ABC ≌△BAD,需要添加一个什么条件?请说明理由.
(1) ( );
(2) ( );
(3) ( );
(4) ( ).
AD = BC
AC = BD
∠DAB = ∠CBA
∠DBA = ∠CAB
HL
HL
AAS
AAS
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例3
如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠B和∠F的大小有什么关系?
解
在Rt△ABC和Rt△DEF中,
BC=EF,
AC=DF ,
∴ Rt△ABC≌Rt△DEF (HL).
∴∠B=∠DEF.
∵ ∠DEF+∠F=90°,
∴∠B+∠F=90°.
例题讲解
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
例4
如图,两根长度均为12m的绳子,一端系在旗杆上,另一端分别固定在地面的两个木桩上,两个木桩离旗杆底部的距离相等吗 请说明你的理由.
解
∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在Rt△ABD和Rt △ACD中,
∴Rt△ABD≌Rt △ACD(HL),
∴BD=CD.
AB=AC,
∠ADB=∠ADC ,
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.如图,C 是路段AB 的中点,两人从C 同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地.DA⊥AB,EB⊥AB. D,E 与路段AB的距离相等吗?为什么?
A
B
C
D
E
分析:CA=CB
CD=CE
∠A=∠B=90°
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.如图,C 是路段AB 的中点,两人从C 同时出发,以相同的速度分别沿两条直线行走,并同时到达D,E两地.DA⊥AB,EB⊥AB. D,E 与路段AB的距离相等吗?为什么?
A
B
C
D
E
解:D,E与线段AB的距离相等.
∵C是路段AB的中点,
∴AC=BC.
∵DA⊥AB , EB⊥AB ,
∴∠A=∠B=90°.
CD=CE,
AC=CB,
在Rt△ADC 和Rt△BEC 中,
∴ Rt△ADC ≌ Rt△BEC (HL).
∴ AD =BE.
∴ D,E与线段AB的距离相等.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
2.如图,AB =CD,AE⊥BC,DF⊥BC,垂足分别为E ,F,CE =BF.求证:(1)AE =DF ; (2)CD//AB.
A
B
C
D
E
F
分析: CE-EF=BF-EF,即CF=BE
Rt△ABE ≌ Rt△DCF(HL)
AE=DF
∠B=∠C
CD//AB
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
2.如图,AB =CD,AE⊥BC,DF⊥BC,垂足分别为E ,F,CE =BF.求证:(1)AE =DF ; (2)CD//AB.
A
B
C
D
E
F
证明:∵CE=BF,
∵AE⊥BC , DF⊥BC ,
∴∠AEB=∠DFC=90°.
AB=DC,
CF=BE,
在Rt△ABE 和Rt△DCF 中,
∴ Rt△ABE ≌ Rt△DCF (HL).
∴ AE=DF , ∠B=∠C.
∴ CD//AB.
∴CE-EF=BF-EF,即CF=BE.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
3.如图,已知AB=AC,AE=AF, AE⊥EC,AF⊥BF,
垂足分别是点E、F.求证:∠1=∠2.
A
B
C
E
F
1
2
证明:∵ AE⊥EC,AF⊥BF ,
∴∠E=∠F=90°.
在Rt△AEC 和 Rt△AFB 中,
AC =AB,
AE =AF,
∴Rt△AEC ≌ Rt△AFB(HL).
∴∠EAC=∠FAB.
∴∠EAC-∠BAC=∠FAB-∠BAC.
∴∠1=∠2.
对照练习
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
4.如图 在△ABC中,已知BD⊥AC,CE ⊥AB,BD=CE.求证:△EBC≌△DCB.
A
B
C
E
D
证明:∵ BD⊥AC,CE⊥AB,
∴∠BEC=∠BDC=90 °.
在 Rt△EBC 和Rt△DCB 中,
CE=BD,
BC=CB .
∴ Rt△EBC≌Rt△DCB (HL).
对应中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
1.(2025·重庆)学习了角平分线和尺规作图后,小红进行了拓展性研究,她发现了角平分线的另一种作法,并与她的同伴进行交流,现在你作为她的同伴,请根据她的想法与思路,完成以下作图和填空:
第一步:构造角平分线.
小红在∠AOB的边OA上任取一点E,并过点E作了OA的垂线(如图).请你利用尺规作图,在OB边上截取OF=OE,过点F作OB的垂线与小红所作的垂线交于点P,作射线OP,OP即为∠AOB的平分线(不写作法,保留作图痕迹).
第二步:利用三角形全等证明她的猜想.
证明:∵PE⊥OA,PF⊥OB,
∴∠OEP=∠OFP=90°.
在RtΔOEP和RtΔOFP中,
① ,
② ,
∴ Rt ΔOEP≌Rt ΔOFP(HL)
∴ ③ .
∴OP平分∠AOB
①PO=PO; ②OE=OF;③∠EOP= ∠FOP
对应中考
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
2.(2023·浙江)如图,在RtΔABC中,∠ACB=90°,0为AC边上一点,连结OB,以OC为半径的半圆与AB边相切于点D,交AC边于点E.
求证:BC=BD.
证明:如图,连接OD,
∵BD是⊙O的切线,点D为切点,
∴∠ODB=90°,
∠ACB=90°,
∴RtΔODB≌RtΔOCB(HL).
∴BC=BD.
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
我亲历了什么
我知道了什么
我会什么
用“HL”判定直角三角形全等
独立书写用“HL”判定直角三角形全等的步骤
推导判定两个直角三角形全等的条件
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
斜边和一直角边分别相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”)
基本事实:
知识点 用“HL”判定直角三角形全等
(1)“HL”是仅适用于直角三角形的特殊方法.
两个“△”前要加“Rt”.
(2)注意对应相等.
”HL”中“H”代表斜边,“L”代表直角边.
“斜边-直角边”顺序不要混淆.
在Rt△ABC 与 Rt△A′B′C′ 中,
∴Rt△ABC≌Rt△A′B′C′ (HL)
AB =A′B′
BC = B′C′
课堂小结
情境导入
合作探究
抽象概括
课堂练习
示范讲解
课堂小结
课后作业
A层:P43:习题14.2:11题.
B层:P43:习题14.2:12题.
下 课
同课章节目录
