苏教版高中数学选择性必修第一册第四章数列4.2.3等差数列前n项和(1) 课件(共22张PPT)
文档属性
| 名称 | 苏教版高中数学选择性必修第一册第四章数列4.2.3等差数列前n项和(1) 课件(共22张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 12:53:57 | ||
图片预览






文档简介
(共22张PPT)
4.2.3 等差数列的前n项和(1)
学习目标:
1.掌握等差数列的前n项和公式,并能运用公式解决一些简单问题.
2.体会等差数列前n项和公式与二次函数间的关系.
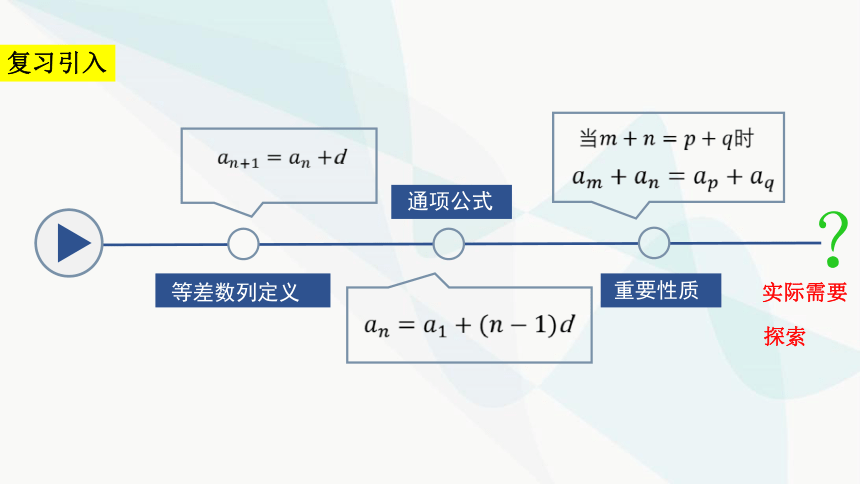
复习引入
等差数列定义
通项公式
重要性质
?
实际需要
探索
数学建构
世界七大奇迹之一的泰姬陵传说(泰姬陵坐落于印度古都阿格,是十七世纪莫卧儿帝国皇帝沙杰罕为纪念其爱妃所建,它宏伟壮观,纯白大理石砌建而成的主体建筑叫人心醉神迷,陵寝以宝石镶饰,图案之细致令人叫绝,成为世界七大奇迹之一。)
传说陵寝中有一个三角形图案,以相同大小的圆宝石镶饰而成,共有 100 层, 你知道这个图案一共花了多少宝石吗?
情景引入
等差数列前n项和
定义:
合作探究
……
……
…
你知道这个图案一共花了多少宝石吗?
如何计算
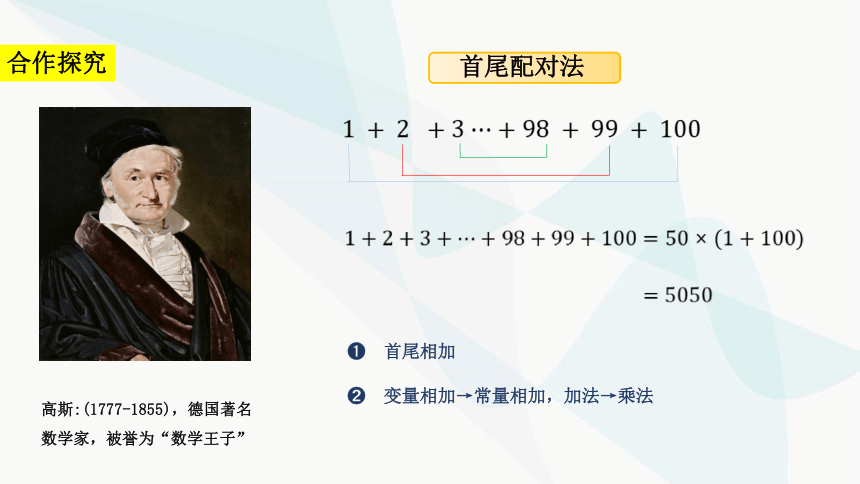
合作探究
高斯:(1777-1855),德国著名数学家,被誉为“数学王子”
首尾相加
变量相加→常量相加,加法→乘法
首尾配对法
合作探究
与奇偶性无关
奇偶分析法
→ 存在避免分类讨论的方法→ 怎样操作?
合作探究
①
②
①+②可得
1
2
n
n+1
n+1
n+1
倒置拼补法
倒序相加法
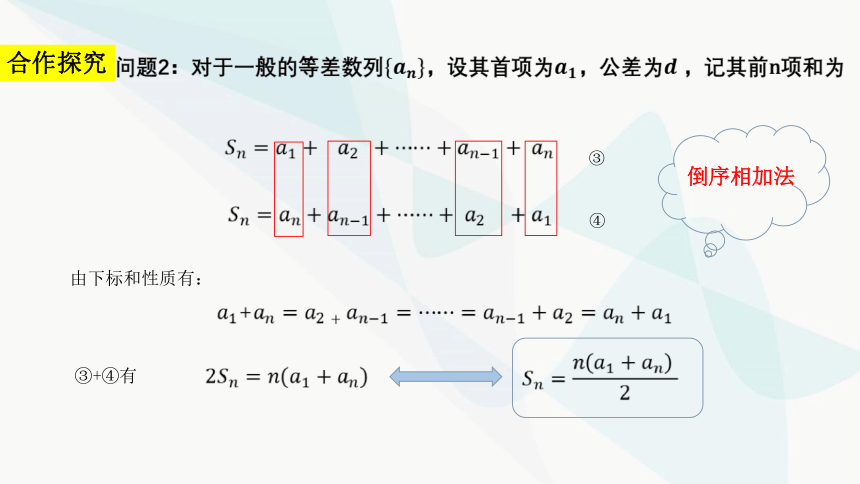
合作探究
③
④
由下标和性质有:
③+④有
倒序相加法
方法总结
不同数的求和
相同数的求和
一般
特殊
等差数列前n项和公式:
数学建构
数学应用
你有什么发现?
知 三 求 二
(3)d=2,an=11,Sn=35,求a1和n.
数学应用
例1.在等差数列{an}中,
数学应用
法一:(基本量法)
法二:(函数思想)待定系数法,设
例3:南北朝时张丘建在《张丘建算经》里给出了几个等差数列的问题:
(1)”今有女子不善织布,逐日所织之布以同数递减,初日织五尺, 末一日织一尺,计织三十日,问共织几何?”
(2)今有女子善织布,逐日所织的布以同数递增,初日织五尺,计织三十日,共织九匹三丈,问日增几何?”(一匹为四丈,一丈为10尺)
d=
数学应用
1、求和的重要方法之一:倒序相加法
2、等差数列前n项和公式:
3、求等差数列基本量方法:
①方程思想;②函数思想
课堂小结
1.在等差数列{an}中,若3S3=S2+S4,a1=2,则a5=( )
A.-12 B.-10 C.10 D.12
3.数列{an}为等差数列,它的前n项和为Sn,若Sn=(n+1)2+λ,则λ的值为________.
4. S5=24,则a2+a4= .
课堂达标
谢谢
公式的再认识
公式的再认识
公式的再认识
公式的再认识
4.2.3 等差数列的前n项和(1)
学习目标:
1.掌握等差数列的前n项和公式,并能运用公式解决一些简单问题.
2.体会等差数列前n项和公式与二次函数间的关系.
复习引入
等差数列定义
通项公式
重要性质
?
实际需要
探索
数学建构
世界七大奇迹之一的泰姬陵传说(泰姬陵坐落于印度古都阿格,是十七世纪莫卧儿帝国皇帝沙杰罕为纪念其爱妃所建,它宏伟壮观,纯白大理石砌建而成的主体建筑叫人心醉神迷,陵寝以宝石镶饰,图案之细致令人叫绝,成为世界七大奇迹之一。)
传说陵寝中有一个三角形图案,以相同大小的圆宝石镶饰而成,共有 100 层, 你知道这个图案一共花了多少宝石吗?
情景引入
等差数列前n项和
定义:
合作探究
……
……
…
你知道这个图案一共花了多少宝石吗?
如何计算
合作探究
高斯:(1777-1855),德国著名数学家,被誉为“数学王子”
首尾相加
变量相加→常量相加,加法→乘法
首尾配对法
合作探究
与奇偶性无关
奇偶分析法
→ 存在避免分类讨论的方法→ 怎样操作?
合作探究
①
②
①+②可得
1
2
n
n+1
n+1
n+1
倒置拼补法
倒序相加法
合作探究
③
④
由下标和性质有:
③+④有
倒序相加法
方法总结
不同数的求和
相同数的求和
一般
特殊
等差数列前n项和公式:
数学建构
数学应用
你有什么发现?
知 三 求 二
(3)d=2,an=11,Sn=35,求a1和n.
数学应用
例1.在等差数列{an}中,
数学应用
法一:(基本量法)
法二:(函数思想)待定系数法,设
例3:南北朝时张丘建在《张丘建算经》里给出了几个等差数列的问题:
(1)”今有女子不善织布,逐日所织之布以同数递减,初日织五尺, 末一日织一尺,计织三十日,问共织几何?”
(2)今有女子善织布,逐日所织的布以同数递增,初日织五尺,计织三十日,共织九匹三丈,问日增几何?”(一匹为四丈,一丈为10尺)
d=
数学应用
1、求和的重要方法之一:倒序相加法
2、等差数列前n项和公式:
3、求等差数列基本量方法:
①方程思想;②函数思想
课堂小结
1.在等差数列{an}中,若3S3=S2+S4,a1=2,则a5=( )
A.-12 B.-10 C.10 D.12
3.数列{an}为等差数列,它的前n项和为Sn,若Sn=(n+1)2+λ,则λ的值为________.
4. S5=24,则a2+a4= .
课堂达标
谢谢
公式的再认识
公式的再认识
公式的再认识
公式的再认识
