苏教版高中数学选择性必修第一册第五章导数及其应用5.1.2瞬时变化率导数 课件(共16张PPT)
文档属性
| 名称 | 苏教版高中数学选择性必修第一册第五章导数及其应用5.1.2瞬时变化率导数 课件(共16张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 895.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
5.1 .2瞬时变化率-导数
学习目标
(1)知道平均变化率与瞬时变化率的关系;能正确区分平均变化率与瞬时变化率;会描述导数概念的实际背景,知道瞬时变化率就是导数,体会导数的思想及其内涵.
(2)会依据定义求简单函数在某点处的导数,能初步按定义归纳求函数在某点处导数的基本步骤.
(3)通过从实例——速度——变化率的抽象过程,培养学生观察、分析、比较、归纳与类比能力,体验从特殊到一般的研究问题方法.
(4)感受导数在解决实际问题中的作用,体会导数思想的作用与价值.
(5)通过导数概念形成的系列探究活动,进一步认识合作学习的意义,增强学生的合作交流意识与能力.
情景引入
“人类精神的
最高胜利”
牛顿
莱布尼茨
问题情景
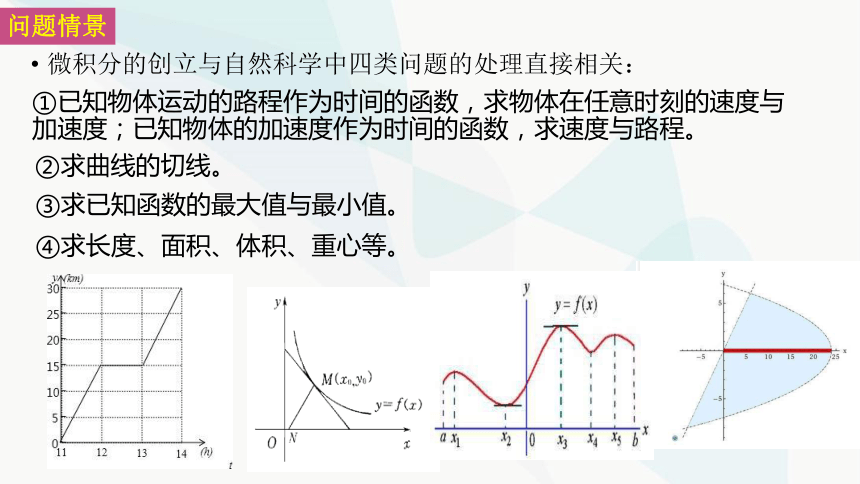
微积分的创立与自然科学中四类问题的处理直接相关:
①已知物体运动的路程作为时间的函数,求物体在任意时刻的速度与 加速度;已知物体的加速度作为时间的函数,求速度与路程。
②求曲线的切线。
③求已知函数的最大值与最小值。
④求长度、面积、体积、重心等。
问题情景
探究:某高台跳水运动员距水面的高度与起跳后的时间存在函数关系:
(2)你认为用平均速度描述运动员的运动状态有什么问题吗?
如何解决这个问题?
(1)运动员在这段时间里是静止的吗?
计算运动员在 这段时间里的平均速度;
思考并回答下面的问题:
h
t
o
1. 平均速度能否精确反映它的运动状态
2.如何精确描述物体在某一时刻的运动状态
思考:
瞬时速度:物体在某一时刻的速度。
如何求呢?
利用激光反射测出指定时间内汽车的移动距离,通过计算得出这段时间的平均速度.测速时间非常短,因此可用这段时间的平均速度近似刻画这段时间内任意时刻的瞬时速度.
问题情景
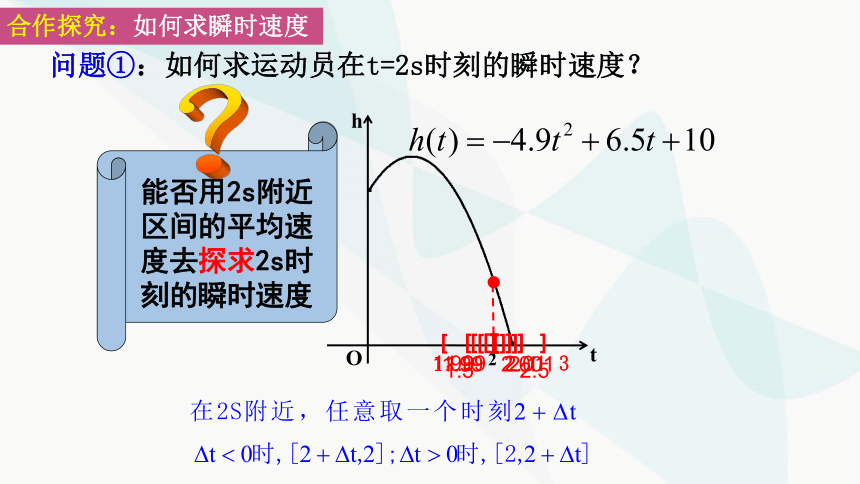
合作探究:如何求瞬时速度
问题①:如何求运动员在t=2s时刻的瞬时速度?
O
t
h
2
[ ]
1
[ ]
1.5
[ ]
1.9
[ ]
1.99
[]
1.999
[ ]
3
[ ]
2.5
[ ]
2.1
[ ]
2.01
[]
2.001
能否用2s附近区间的平均速度去探求2s时刻的瞬时速度
合作探究
在[2+△t,2]这段时间内
在[2,2 +△t]这段时间内
△t>0时
△t<0时
我们先考察该运动员在t=2S时刻附近的平均速度:
-0.1 0.1
-0.01 0.01
-0.001 0.001
-0.0001 0.0001
-0.00001 0.00001
…… ……
△t<0 时,在[2+△t,2]
这段时间内
△t>0,在[2,2 +△t]这段时间内
-12.61
-13.59
问题②:计算下列表格各个区间内的平均速度
合作探究
△t<0,在[2+△t,2]这段时间内
△t>0,在[2,2 +△t]这段时间内
-0.1 -12.61 0.1 -13.59
-0.01 -13.051 0.01 -13.149
-0.001 -13.0951 0.001 -13.1049
-0.0001 -13.09951 0.0001 -13.10049
-0.00001 -13.099951 0.00001 -13.100049
…… ……
问③:Δt趋近于0时,平均速度有怎样的变化趋势?
当t=2,Δt趋近于0时,平均速度就无限趋近于一个确定值,这个确定值就是t=2时刻的瞬时速度
合作探究
t=2s时刻的瞬时速度:
数学符号表示为:
合作探究
问题⑤ :如果将上述问题中的函数 用 来表示,那么函数 在 处的瞬时变化率如何表示呢?
问题④:运动员在某个时刻 的瞬时速度如何表示呢?
数学建构
函数 在 处的瞬时变化率
称为函数 在 处的导数,记作
或
即
导数可以描述任何事物的瞬时变化率。
数学建构
数学应用
练习:求函数f(x)=x2在x=1处的导数.
数学应用
例1 将原油精炼为汽油、柴油、塑胶等各种不同产品, 需要对原油进行冷却和加热. 如果第 x h时, 原油的温度(单位: )为 f (x) = x2 – 7x+15 ( 0≤x≤8 ) . 计算第2h和第6h, 原油温度的瞬时变化率, 并说明它们的意义.
数学应用
解: 在第2h和第6h时, 原油温度的瞬时变化率就是
和
根据导数的定义,
所以,
同理可得
在第2h和第6h时, 原油温度的瞬时变化率分别为–3和5. 它说明在第2h附近, 原油温度大约以3 / h的速率下降; 在第6h附近,原油温度大约以5 / h的速率上升.
课堂小结
1、知识点:
2、主要的思想方法:
导数的概念(瞬时变化率);
逼近.
5.1 .2瞬时变化率-导数
学习目标
(1)知道平均变化率与瞬时变化率的关系;能正确区分平均变化率与瞬时变化率;会描述导数概念的实际背景,知道瞬时变化率就是导数,体会导数的思想及其内涵.
(2)会依据定义求简单函数在某点处的导数,能初步按定义归纳求函数在某点处导数的基本步骤.
(3)通过从实例——速度——变化率的抽象过程,培养学生观察、分析、比较、归纳与类比能力,体验从特殊到一般的研究问题方法.
(4)感受导数在解决实际问题中的作用,体会导数思想的作用与价值.
(5)通过导数概念形成的系列探究活动,进一步认识合作学习的意义,增强学生的合作交流意识与能力.
情景引入
“人类精神的
最高胜利”
牛顿
莱布尼茨
问题情景
微积分的创立与自然科学中四类问题的处理直接相关:
①已知物体运动的路程作为时间的函数,求物体在任意时刻的速度与 加速度;已知物体的加速度作为时间的函数,求速度与路程。
②求曲线的切线。
③求已知函数的最大值与最小值。
④求长度、面积、体积、重心等。
问题情景
探究:某高台跳水运动员距水面的高度与起跳后的时间存在函数关系:
(2)你认为用平均速度描述运动员的运动状态有什么问题吗?
如何解决这个问题?
(1)运动员在这段时间里是静止的吗?
计算运动员在 这段时间里的平均速度;
思考并回答下面的问题:
h
t
o
1. 平均速度能否精确反映它的运动状态
2.如何精确描述物体在某一时刻的运动状态
思考:
瞬时速度:物体在某一时刻的速度。
如何求呢?
利用激光反射测出指定时间内汽车的移动距离,通过计算得出这段时间的平均速度.测速时间非常短,因此可用这段时间的平均速度近似刻画这段时间内任意时刻的瞬时速度.
问题情景
合作探究:如何求瞬时速度
问题①:如何求运动员在t=2s时刻的瞬时速度?
O
t
h
2
[ ]
1
[ ]
1.5
[ ]
1.9
[ ]
1.99
[]
1.999
[ ]
3
[ ]
2.5
[ ]
2.1
[ ]
2.01
[]
2.001
能否用2s附近区间的平均速度去探求2s时刻的瞬时速度
合作探究
在[2+△t,2]这段时间内
在[2,2 +△t]这段时间内
△t>0时
△t<0时
我们先考察该运动员在t=2S时刻附近的平均速度:
-0.1 0.1
-0.01 0.01
-0.001 0.001
-0.0001 0.0001
-0.00001 0.00001
…… ……
△t<0 时,在[2+△t,2]
这段时间内
△t>0,在[2,2 +△t]这段时间内
-12.61
-13.59
问题②:计算下列表格各个区间内的平均速度
合作探究
△t<0,在[2+△t,2]这段时间内
△t>0,在[2,2 +△t]这段时间内
-0.1 -12.61 0.1 -13.59
-0.01 -13.051 0.01 -13.149
-0.001 -13.0951 0.001 -13.1049
-0.0001 -13.09951 0.0001 -13.10049
-0.00001 -13.099951 0.00001 -13.100049
…… ……
问③:Δt趋近于0时,平均速度有怎样的变化趋势?
当t=2,Δt趋近于0时,平均速度就无限趋近于一个确定值,这个确定值就是t=2时刻的瞬时速度
合作探究
t=2s时刻的瞬时速度:
数学符号表示为:
合作探究
问题⑤ :如果将上述问题中的函数 用 来表示,那么函数 在 处的瞬时变化率如何表示呢?
问题④:运动员在某个时刻 的瞬时速度如何表示呢?
数学建构
函数 在 处的瞬时变化率
称为函数 在 处的导数,记作
或
即
导数可以描述任何事物的瞬时变化率。
数学建构
数学应用
练习:求函数f(x)=x2在x=1处的导数.
数学应用
例1 将原油精炼为汽油、柴油、塑胶等各种不同产品, 需要对原油进行冷却和加热. 如果第 x h时, 原油的温度(单位: )为 f (x) = x2 – 7x+15 ( 0≤x≤8 ) . 计算第2h和第6h, 原油温度的瞬时变化率, 并说明它们的意义.
数学应用
解: 在第2h和第6h时, 原油温度的瞬时变化率就是
和
根据导数的定义,
所以,
同理可得
在第2h和第6h时, 原油温度的瞬时变化率分别为–3和5. 它说明在第2h附近, 原油温度大约以3 / h的速率下降; 在第6h附近,原油温度大约以5 / h的速率上升.
课堂小结
1、知识点:
2、主要的思想方法:
导数的概念(瞬时变化率);
逼近.
