苏教版高中数学选择性必修第一册第1章直线与方程1.2.2直线的两点式方程 课件(共52张PPT)
文档属性
| 名称 | 苏教版高中数学选择性必修第一册第1章直线与方程1.2.2直线的两点式方程 课件(共52张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 00:00:00 | ||
图片预览











文档简介
(共52张PPT)
苏教版2019高二数学(选修一)第一章 直线与方程
1.2.2 直线的两点式方程
学习目标
1.根据确定直线位置的几何要素,探索并掌握直
线的两点式方程.
2.了解直线的截距式方程的形式特征及适用范围.
1、直线的点斜式方程
2、直线的斜截式方程
3、直线的点斜式方程和斜截式方程之间的关系
斜截式是点斜式的特殊情况,两者均不能表示斜率不存在即与x轴垂直的直线。
复习回顾
情景导入
生活中“两点确定一条直线”的例子随处可见,比如我们在植树时,只要定出两个树坑的位置就能够确定同一行的树坑所在的直线.那么在直角坐标系内,已知直线上两点,如何求直线的方程呢?
直线的两点式方程
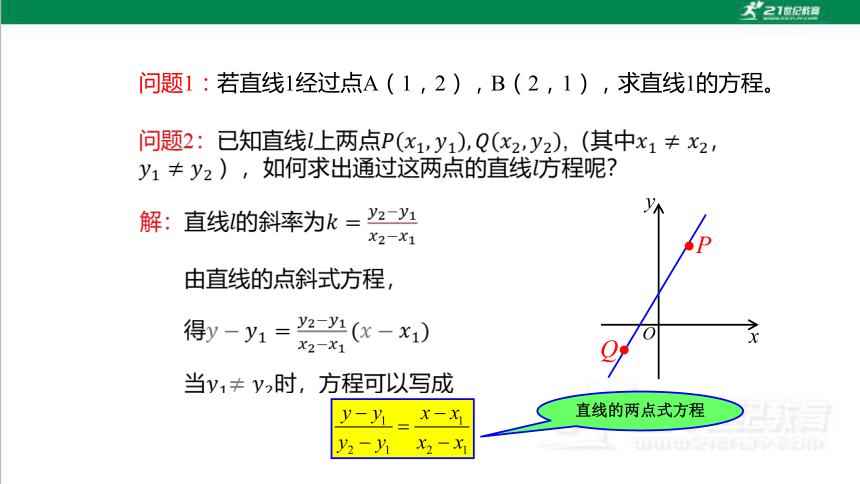
问题1:若直线1经过点A(1,2),B(2,1),求直线1的方程。
(3)方程 能表示平面内任意一条直线。
1、直线的两点式方程
新知探究
说明:(1)这个方程由直线上两点确定;
(2)当直线没有斜率或斜率为0时,不能用两点式求出它们的方程。
即:直线的两点式方程不能表示与坐标轴(x轴与y轴)平行的直线;
课本例3 已知直线l经过两点A(a,0),B(0,b)(如图),其中a≠0,b≠0,求直线l的方程.
典例剖析
利用两点式求直线的方程
(1)首先要判断是否满足两点式方程的适用条件,若满足即可考虑用两点式求方程.
(2)在斜率存在的情况下,也可以先应用斜率公式求出斜率,再用点斜式写方程.
概念归纳
练一练
练一练
2、直线的截距式方程
新知探究
注意:直线的截距式方程不能表示与坐标轴(x轴与y轴)平行或经过原点的直线。
课本例4 已知三角形的顶点是A(-5,0),B(3,-3),C(0,2)(如图),
分别求这个三角形三边所在直线的方程.
方程 适用范围
点斜式 不垂直于x轴的直线
斜截式 不垂直于x轴的直线
两点式 不垂直于坐标轴的直线
截距式 不垂直于坐标轴且不经过原点的直线
★四种直线方程及其适用范围★
概念归纳
下列四个命题中正确的是( )
(A)经过定点P0 (x0,y0)的直线都可以用方程y-y0=k(x-x0)
表示;
(B)经过任意两个不同点P1 (x1,y1)、 P2 (x2,y2)的直线都可
以用方程(y-y1)(x2-x1) = (x-x1)(y2-y1)表示;
(C)不经过原点的直线都可以用方程 表示;
(D)经过定点的直线都可以用方程y=kx+b表示。
B
练一练
典例剖析
截距式方程应用的注意事项
(1)如果问题中涉及直线与坐标轴相交,则可考虑选用截距式方程,用待定系数法确定其系数即可.
(2)选用截距式方程时,必须首先考虑直线是否过原点以及是否与两坐标轴垂直.
(3)要注意截距式方程的逆向应用.
概念归纳
练一练
典例剖析
直线方程的选择技巧
(1)已知一点的坐标,求过该点的直线方程,一般选取点斜式方程,再由其他条件确定直线的斜率.
(2)若已知直线的斜率,一般选用直线的斜截式,再由其他条件确定直线的一个点或者截距.
(3)若已知两点坐标,一般选用直线的两点式方程,若两点是与坐标轴的交点,就用截距式方程.
(4)不论选用怎样的直线方程,都要注意各自方程的限制条件,对特殊情况下的直线要单独讨论解决.
概念归纳
练一练
随堂练
1.在x轴、y轴上的截距分别是-3,4的直线方程是( )
答案 A
3.过点P(1,2)且在两坐标轴上截距的和为0的直线方程为________________________.
答案 2x-y=0或x-y+1=0
分层练习-基础
分层练习-基础
答案 A
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
答案 D
分层练习-基础
分层练习-基础
答案 2023
分层练习-基础
分层练习-基础
分层练习-巩固
答案 AC
分层练习-巩固
分层练习-巩固
分层练习-巩固
答案 x+2y-6=0
分层练习-巩固
分层练习-巩固
分层练习-拓展
答案 3
分层练习-拓展
方程 适用范围
点斜式 不垂直于x轴的直线
斜截式 不垂直于x轴的直线
两点式 不垂直于坐标轴的直线
截距式 不垂直于坐标轴且不经过原点的直线
★四种直线方程及其适用范围★
课堂小结
苏教版2019高二数学(选修一)第一章 直线与方程
1.2.2 直线的两点式方程
学习目标
1.根据确定直线位置的几何要素,探索并掌握直
线的两点式方程.
2.了解直线的截距式方程的形式特征及适用范围.
1、直线的点斜式方程
2、直线的斜截式方程
3、直线的点斜式方程和斜截式方程之间的关系
斜截式是点斜式的特殊情况,两者均不能表示斜率不存在即与x轴垂直的直线。
复习回顾
情景导入
生活中“两点确定一条直线”的例子随处可见,比如我们在植树时,只要定出两个树坑的位置就能够确定同一行的树坑所在的直线.那么在直角坐标系内,已知直线上两点,如何求直线的方程呢?
直线的两点式方程
问题1:若直线1经过点A(1,2),B(2,1),求直线1的方程。
(3)方程 能表示平面内任意一条直线。
1、直线的两点式方程
新知探究
说明:(1)这个方程由直线上两点确定;
(2)当直线没有斜率或斜率为0时,不能用两点式求出它们的方程。
即:直线的两点式方程不能表示与坐标轴(x轴与y轴)平行的直线;
课本例3 已知直线l经过两点A(a,0),B(0,b)(如图),其中a≠0,b≠0,求直线l的方程.
典例剖析
利用两点式求直线的方程
(1)首先要判断是否满足两点式方程的适用条件,若满足即可考虑用两点式求方程.
(2)在斜率存在的情况下,也可以先应用斜率公式求出斜率,再用点斜式写方程.
概念归纳
练一练
练一练
2、直线的截距式方程
新知探究
注意:直线的截距式方程不能表示与坐标轴(x轴与y轴)平行或经过原点的直线。
课本例4 已知三角形的顶点是A(-5,0),B(3,-3),C(0,2)(如图),
分别求这个三角形三边所在直线的方程.
方程 适用范围
点斜式 不垂直于x轴的直线
斜截式 不垂直于x轴的直线
两点式 不垂直于坐标轴的直线
截距式 不垂直于坐标轴且不经过原点的直线
★四种直线方程及其适用范围★
概念归纳
下列四个命题中正确的是( )
(A)经过定点P0 (x0,y0)的直线都可以用方程y-y0=k(x-x0)
表示;
(B)经过任意两个不同点P1 (x1,y1)、 P2 (x2,y2)的直线都可
以用方程(y-y1)(x2-x1) = (x-x1)(y2-y1)表示;
(C)不经过原点的直线都可以用方程 表示;
(D)经过定点的直线都可以用方程y=kx+b表示。
B
练一练
典例剖析
截距式方程应用的注意事项
(1)如果问题中涉及直线与坐标轴相交,则可考虑选用截距式方程,用待定系数法确定其系数即可.
(2)选用截距式方程时,必须首先考虑直线是否过原点以及是否与两坐标轴垂直.
(3)要注意截距式方程的逆向应用.
概念归纳
练一练
典例剖析
直线方程的选择技巧
(1)已知一点的坐标,求过该点的直线方程,一般选取点斜式方程,再由其他条件确定直线的斜率.
(2)若已知直线的斜率,一般选用直线的斜截式,再由其他条件确定直线的一个点或者截距.
(3)若已知两点坐标,一般选用直线的两点式方程,若两点是与坐标轴的交点,就用截距式方程.
(4)不论选用怎样的直线方程,都要注意各自方程的限制条件,对特殊情况下的直线要单独讨论解决.
概念归纳
练一练
随堂练
1.在x轴、y轴上的截距分别是-3,4的直线方程是( )
答案 A
3.过点P(1,2)且在两坐标轴上截距的和为0的直线方程为________________________.
答案 2x-y=0或x-y+1=0
分层练习-基础
分层练习-基础
答案 A
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
答案 D
分层练习-基础
分层练习-基础
答案 2023
分层练习-基础
分层练习-基础
分层练习-巩固
答案 AC
分层练习-巩固
分层练习-巩固
分层练习-巩固
答案 x+2y-6=0
分层练习-巩固
分层练习-巩固
分层练习-拓展
答案 3
分层练习-拓展
方程 适用范围
点斜式 不垂直于x轴的直线
斜截式 不垂直于x轴的直线
两点式 不垂直于坐标轴的直线
截距式 不垂直于坐标轴且不经过原点的直线
★四种直线方程及其适用范围★
课堂小结
