苏教版高中数学选择性必修第一册第1章直线与方程1.2.1直线的点斜式、斜截式方程课件(共59张PPT)
文档属性
| 名称 | 苏教版高中数学选择性必修第一册第1章直线与方程1.2.1直线的点斜式、斜截式方程课件(共59张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 00:00:00 | ||
图片预览










文档简介
(共59张PPT)
苏教版2019高二数学(选修一)第一章 直线与方程
1.2.1 直线的点斜式、斜截式方程
学习目标
1.了解由斜率公式推导直线方程的点斜式的过程.
2.掌握直线的点斜式方程与斜截式方程.
3.会利用直线的点斜式方程与斜截式方程解决有关的问题.
飞逝的流星形成了一条美丽的弧线,这条弧线可以看做是满足某种运动规律的点的集合.在平面直角坐标系中,直线也可以看做是满足某种条件的点的集合,直线的位置既可由两点惟一确定,也可由一点和一个方向来确定.
情景导入
2、直线斜率的两个定义
3、直线倾斜角和斜率的取值范围
1、直线倾斜角的定义
在平面直角坐标系中,对于一条与x轴相交的直线l,把 x轴所在的直线绕着交点按逆时针方向旋转到和直线l重合时所转过的最小正角称为直线l的倾斜角。
注意:(1)直线向上方向; (2)x轴的正方向。
复习回顾
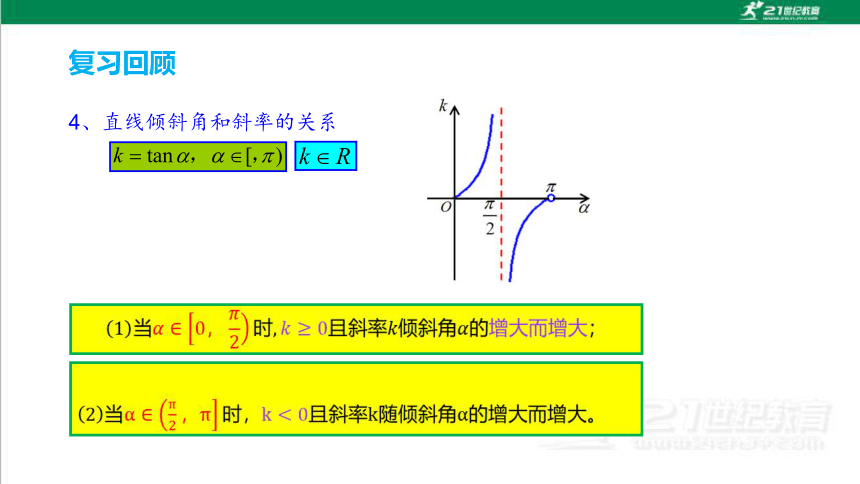
4、直线倾斜角和斜率的关系
复习回顾
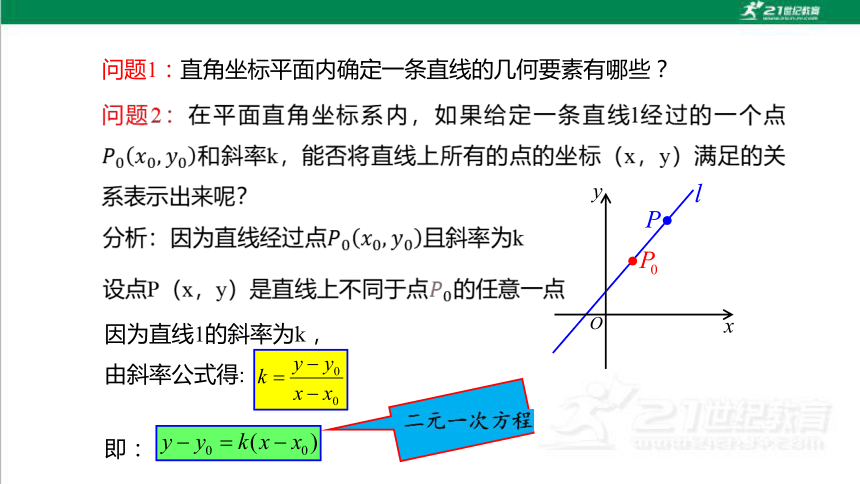
问题1:直角坐标平面内确定一条直线的几何要素有哪些?
因为直线1的斜率为k,
由斜率公式得:
即:
1.直线的点斜式方程
新知探究
与x轴平行的直线倾斜角为0°,
其斜率 k = tan 0° = 0,
故与x轴平行的直线方程为:
x轴所在直线的倾斜角为0°,其斜率k = tan 0° = 0,
故x轴所在直线方程为:
问题4:坐标轴或与坐标轴平行的直线方程怎么表示?
(1)x轴所在直线的方程是什么?
即:
与y轴平行的直线倾斜角为90°,其斜率不存在,
不能用点斜式方程表示,
故y轴所在直线方程为:
问题4:坐标轴或与坐标轴平行的直线方程怎么表示?
(3)y轴所在直线的方程是什么?
故y轴所在直线方程为:
y轴所在直线的倾斜角为90°其斜率不存在,不能用点斜式方程表示,
问题5:直线的点斜式方程能表示坐标平面上的所有直线吗?
当直线的斜率不存在(即与y轴重合或平行)时,直线的方程不可以用点斜式来表示。
课本例1 已知一直线经过点P(-2,3),斜率为2,求这条直线的方程.
解 由直线的点斜式方程,得所求直线的方程为y-3=2(x+2),
即2x-y+7=0.
课本例题
典例剖析
例1 写出下列直线的点斜式方程:
(1)经过点(2,5),倾斜角为45°;
(2)直线y=x+1绕着其上一点P(3,4)逆时针旋转90°后得直线l,求直线l的点斜式方程;
(3)经过点C(-1,-1),且与x轴平行;
(4)经过点D(1,1),且与x轴垂直.
解 (1)因为倾斜角为45°,
所以斜率k=tan 45°=1,
所以直线的方程为y-5=x-2.
(2)直线y=x+1的斜率k=1,所以倾斜角为45°.
由题意知,直线l的倾斜角为135°,
所以直线l的斜率k′=tan 135°=-1.
所以直线的方程为y-4=-(x-3).
(3)由题意知,直线的斜率k=tan 0°=0,
所以直线的点斜式方程为y-(-1)=0,
即y=-1.
(4)由题意可知直线的斜率不存在,所以直线的方程为x=1, 该直 线没有点斜式方程.
概念归纳
求直线的点斜式方程的步骤及注意点
(1)求直线的点斜式方程的步骤:定点(x1,y1)→定斜率k→写出方程y-y1=k(x-x1).
(2)点斜式方程y-y1=k(x-x1)可表示过点P(x1,y1)的所有直线,但x=x1除外.
练一练
课本例2:
直线l上给定一个点P0(0,b)和斜率k,求直线l的方程.
解:由直线的点斜式方程,得直线1的方程为y-b=k(x-0),即y=kx+b.
课本例题
其中,b为直线与y轴交点的纵坐标。我们称b为直线l 在y轴上的截距。
2.直线的斜截式方程
新知探究
方程y=kx+b由直线的斜率与它在y轴上的截距确定,把这个方程叫做直线的斜截式方程,
简称斜截式(Slope intercept form)。
问题6:截距是距离吗?两者有什么区别?如何定义直线在x 轴上的截距?
截距是直线与坐标轴交点的坐标,它可正、可负、可为零,而距离是恒大于等于0的。
当直线与x轴相交时,我们把直线与x轴交点的横坐标叫做直线在x轴上的截距,简称横截距。
问题7:观察方程y=kx+b,它的形式有什么特点?此方程能表示平面内所有直线吗?
我们发现:方程左端的系数恒为1,方程右端x的系数k和常数项b均有明显的几何意义。
k是直线的斜率,b是直线在y轴上的截距。
问题8:斜截式与点斜式存在什么关系?
斜截式是点斜式的特殊情况,有时比点斜式更方便
问题9:斜截式y=kx+b在形式上与一次函数的表达式一样,
它们之间有什么差别?
只有当k≠0时,斜截式方程才是一次函数的表达式
例2 根据条件写出下列直线的斜截式方程:
(1)斜率是3,在y轴上的截距是-3;
(2)倾斜角是60°,在y轴上的截距是5;
(3)过点A(-1,-2),B(-2,3).
典例剖析
求直线的斜截式方程的策略
(1)斜截式方程的应用前提是直线的斜率存在.
(2)直线的斜截式方程y=kx+b中只有两个参数,因此要确定直线方程只需两个独立条件即可.
概念归纳
练一练
练一练
例3、求下列直线的点斜式方程
(1)直线经过点P(-2,3),斜率为2;
(2)直线经过点A (-1,2),且倾斜角α=135o;
(3)直线的斜率为2,经过点(0,1)。
典例剖析
3.利用点斜式、斜截式求直线方程
已知直线的斜率为k,与y轴的交点是P(0,b),求这条直线的方程。
当直线与y轴相交时,我们把直线与y轴交点的纵坐标b叫做直线在y轴上的截距,简称纵截距。
即:
例4 (1)已知直线kx-y+1-3k=0,当k变化时,所有的直线恒过定点( )
A.(1,3) B.(-1,-3)
C.(3,1) D.(-3,-1)
答案 C
典例剖析
1.若本例(1)中直线不经过第四象限,求k的取值范围.
(1)解含参数的直线恒过定点问题,可将直线方程整理成y-y0=k(x-x0)的形式,则表示的直线必过定点(x0,y0).
(2)在求面积时,要将截距转化为距离.
概念归纳
(1)若y=a|x|与y=x+a(a>0)有两个公共点,则a的取值范围是( )
A.a>1 B.0C.a=1 D.01
答案 A
练一练
解析 y=x+a(a>0)表示斜率为1,在y轴上的截距为a(a>0)的直线,
y=a|x|表示关于y轴对称的两条射线.
所以当0当a>1时,有两个公共点,如图②.
1.方程y=k(x-2)表示( )
A.过点(-2,0)的所有直线
B.过点(2,0)的所有直线
C.过点(2,0)且不垂直于x轴的所有直线
D.过点(2,0)且除去x轴的所有直线
答案 C
解析 易验证直线过点(2,0),又直线斜率存在,故直线不垂直于x轴.
随堂练
随堂练
随堂练
4.若直线y=kx+b通过第一、三、四象限,则有( )
A.k>0,b>0 B.k>0,b<0
C.k<0,b>0 D.k<0,b<0
答案 B
解析 直线y=kx+b经过第一、三、四象限,由图知,k>0,b<0.
随堂练
分层练习-基础
1.已知一直线经过点A(3,-2),且与x轴平行,则该直线的方程为( )
A.x=3 B.x=-2
C.y=3 D.y=-2
答案 D
解析 ∵直线与x轴平行,∴其斜率为0,
∴直线的方程为y=-2.
分层练习-基础
2.若直线l的倾斜角为45°,且过点(0,-1),则直线l的方程是( )
A.y-1=x B.y+1=x
C.y-1=-x D.y+1=-x
答案 B
解析 ∵直线l的倾斜角为45°,
∴直线l的斜率为1,
又∵直线l过点(0,-1),
∴直线l的方程为y+1=x.
分层练习-基础
4.直线y=ax+(a≠0)的图形可能是( )
答案 B
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
8.已知△ABC的三个顶点都在第一象限内,A(1,1),B(5,1),∠A=45°,∠B=45°.求:
(1)直线AB的方程;
(2)直线AC和BC的方程.
分层练习-基础
解 (1)因为A(1,1),B(5,1),所以直线AB平行于x轴,所以直线AB的方程为y=1.
(2)由题意知,直线AC的倾斜角为∠A=45°,所以kAC=tan 45°=1.
又直线AC过点A(1,1),所以直线AC的方程为y-1=1×(x-1),即y=x.
同理可知,直线BC的倾斜角为180°-∠B=135°,所以kBC=tan 135°=-1.
又直线BC过点B(5,1),所以直线BC的方程为y-1=-1×(x-5),即y=-x+6.
分层练习-基础
分层练习-巩固
9.已知直线l不经过第三象限,设它的斜率为k,在y轴上的截距为b(b≠0),则( )
A.kb<0 B.kb≤0
C.kb>0 D.kb≥0
答案 B
解析 当k≠0时,∵直线l不经过第三象限,∴k<0,b>0,∴kb<0.
当k=0,b>0时,直线l也不过第三象限,∴kb≤0.
分层练习-巩固
答案 BC
分层练习-巩固
分层练习-巩固
分层练习-拓展
分层练习-拓展
12.已知直线l:y=kx+2k+1.
(1)求证:直线l恒过一个定点;
(2)当-3(1)证明 由y=kx+2k+1,得y-1=k(x+2).
由直线方程的点斜式可知,直线恒过定点(-2,1).
(2)解 设函数f(x)=kx+2k+1,显然其图象是一条直线(如图所示),
1、直线的点斜式方程
2、直线的斜截式方程
3、直线的点斜式方程和斜截式方程之间的关系
斜截式是点斜式的特殊情况,两者均不能表示斜率不存在即与x轴垂直的直线。
课堂小结
苏教版2019高二数学(选修一)第一章 直线与方程
1.2.1 直线的点斜式、斜截式方程
学习目标
1.了解由斜率公式推导直线方程的点斜式的过程.
2.掌握直线的点斜式方程与斜截式方程.
3.会利用直线的点斜式方程与斜截式方程解决有关的问题.
飞逝的流星形成了一条美丽的弧线,这条弧线可以看做是满足某种运动规律的点的集合.在平面直角坐标系中,直线也可以看做是满足某种条件的点的集合,直线的位置既可由两点惟一确定,也可由一点和一个方向来确定.
情景导入
2、直线斜率的两个定义
3、直线倾斜角和斜率的取值范围
1、直线倾斜角的定义
在平面直角坐标系中,对于一条与x轴相交的直线l,把 x轴所在的直线绕着交点按逆时针方向旋转到和直线l重合时所转过的最小正角称为直线l的倾斜角。
注意:(1)直线向上方向; (2)x轴的正方向。
复习回顾
4、直线倾斜角和斜率的关系
复习回顾
问题1:直角坐标平面内确定一条直线的几何要素有哪些?
因为直线1的斜率为k,
由斜率公式得:
即:
1.直线的点斜式方程
新知探究
与x轴平行的直线倾斜角为0°,
其斜率 k = tan 0° = 0,
故与x轴平行的直线方程为:
x轴所在直线的倾斜角为0°,其斜率k = tan 0° = 0,
故x轴所在直线方程为:
问题4:坐标轴或与坐标轴平行的直线方程怎么表示?
(1)x轴所在直线的方程是什么?
即:
与y轴平行的直线倾斜角为90°,其斜率不存在,
不能用点斜式方程表示,
故y轴所在直线方程为:
问题4:坐标轴或与坐标轴平行的直线方程怎么表示?
(3)y轴所在直线的方程是什么?
故y轴所在直线方程为:
y轴所在直线的倾斜角为90°其斜率不存在,不能用点斜式方程表示,
问题5:直线的点斜式方程能表示坐标平面上的所有直线吗?
当直线的斜率不存在(即与y轴重合或平行)时,直线的方程不可以用点斜式来表示。
课本例1 已知一直线经过点P(-2,3),斜率为2,求这条直线的方程.
解 由直线的点斜式方程,得所求直线的方程为y-3=2(x+2),
即2x-y+7=0.
课本例题
典例剖析
例1 写出下列直线的点斜式方程:
(1)经过点(2,5),倾斜角为45°;
(2)直线y=x+1绕着其上一点P(3,4)逆时针旋转90°后得直线l,求直线l的点斜式方程;
(3)经过点C(-1,-1),且与x轴平行;
(4)经过点D(1,1),且与x轴垂直.
解 (1)因为倾斜角为45°,
所以斜率k=tan 45°=1,
所以直线的方程为y-5=x-2.
(2)直线y=x+1的斜率k=1,所以倾斜角为45°.
由题意知,直线l的倾斜角为135°,
所以直线l的斜率k′=tan 135°=-1.
所以直线的方程为y-4=-(x-3).
(3)由题意知,直线的斜率k=tan 0°=0,
所以直线的点斜式方程为y-(-1)=0,
即y=-1.
(4)由题意可知直线的斜率不存在,所以直线的方程为x=1, 该直 线没有点斜式方程.
概念归纳
求直线的点斜式方程的步骤及注意点
(1)求直线的点斜式方程的步骤:定点(x1,y1)→定斜率k→写出方程y-y1=k(x-x1).
(2)点斜式方程y-y1=k(x-x1)可表示过点P(x1,y1)的所有直线,但x=x1除外.
练一练
课本例2:
直线l上给定一个点P0(0,b)和斜率k,求直线l的方程.
解:由直线的点斜式方程,得直线1的方程为y-b=k(x-0),即y=kx+b.
课本例题
其中,b为直线与y轴交点的纵坐标。我们称b为直线l 在y轴上的截距。
2.直线的斜截式方程
新知探究
方程y=kx+b由直线的斜率与它在y轴上的截距确定,把这个方程叫做直线的斜截式方程,
简称斜截式(Slope intercept form)。
问题6:截距是距离吗?两者有什么区别?如何定义直线在x 轴上的截距?
截距是直线与坐标轴交点的坐标,它可正、可负、可为零,而距离是恒大于等于0的。
当直线与x轴相交时,我们把直线与x轴交点的横坐标叫做直线在x轴上的截距,简称横截距。
问题7:观察方程y=kx+b,它的形式有什么特点?此方程能表示平面内所有直线吗?
我们发现:方程左端的系数恒为1,方程右端x的系数k和常数项b均有明显的几何意义。
k是直线的斜率,b是直线在y轴上的截距。
问题8:斜截式与点斜式存在什么关系?
斜截式是点斜式的特殊情况,有时比点斜式更方便
问题9:斜截式y=kx+b在形式上与一次函数的表达式一样,
它们之间有什么差别?
只有当k≠0时,斜截式方程才是一次函数的表达式
例2 根据条件写出下列直线的斜截式方程:
(1)斜率是3,在y轴上的截距是-3;
(2)倾斜角是60°,在y轴上的截距是5;
(3)过点A(-1,-2),B(-2,3).
典例剖析
求直线的斜截式方程的策略
(1)斜截式方程的应用前提是直线的斜率存在.
(2)直线的斜截式方程y=kx+b中只有两个参数,因此要确定直线方程只需两个独立条件即可.
概念归纳
练一练
练一练
例3、求下列直线的点斜式方程
(1)直线经过点P(-2,3),斜率为2;
(2)直线经过点A (-1,2),且倾斜角α=135o;
(3)直线的斜率为2,经过点(0,1)。
典例剖析
3.利用点斜式、斜截式求直线方程
已知直线的斜率为k,与y轴的交点是P(0,b),求这条直线的方程。
当直线与y轴相交时,我们把直线与y轴交点的纵坐标b叫做直线在y轴上的截距,简称纵截距。
即:
例4 (1)已知直线kx-y+1-3k=0,当k变化时,所有的直线恒过定点( )
A.(1,3) B.(-1,-3)
C.(3,1) D.(-3,-1)
答案 C
典例剖析
1.若本例(1)中直线不经过第四象限,求k的取值范围.
(1)解含参数的直线恒过定点问题,可将直线方程整理成y-y0=k(x-x0)的形式,则表示的直线必过定点(x0,y0).
(2)在求面积时,要将截距转化为距离.
概念归纳
(1)若y=a|x|与y=x+a(a>0)有两个公共点,则a的取值范围是( )
A.a>1 B.0
答案 A
练一练
解析 y=x+a(a>0)表示斜率为1,在y轴上的截距为a(a>0)的直线,
y=a|x|表示关于y轴对称的两条射线.
所以当0
1.方程y=k(x-2)表示( )
A.过点(-2,0)的所有直线
B.过点(2,0)的所有直线
C.过点(2,0)且不垂直于x轴的所有直线
D.过点(2,0)且除去x轴的所有直线
答案 C
解析 易验证直线过点(2,0),又直线斜率存在,故直线不垂直于x轴.
随堂练
随堂练
随堂练
4.若直线y=kx+b通过第一、三、四象限,则有( )
A.k>0,b>0 B.k>0,b<0
C.k<0,b>0 D.k<0,b<0
答案 B
解析 直线y=kx+b经过第一、三、四象限,由图知,k>0,b<0.
随堂练
分层练习-基础
1.已知一直线经过点A(3,-2),且与x轴平行,则该直线的方程为( )
A.x=3 B.x=-2
C.y=3 D.y=-2
答案 D
解析 ∵直线与x轴平行,∴其斜率为0,
∴直线的方程为y=-2.
分层练习-基础
2.若直线l的倾斜角为45°,且过点(0,-1),则直线l的方程是( )
A.y-1=x B.y+1=x
C.y-1=-x D.y+1=-x
答案 B
解析 ∵直线l的倾斜角为45°,
∴直线l的斜率为1,
又∵直线l过点(0,-1),
∴直线l的方程为y+1=x.
分层练习-基础
4.直线y=ax+(a≠0)的图形可能是( )
答案 B
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
8.已知△ABC的三个顶点都在第一象限内,A(1,1),B(5,1),∠A=45°,∠B=45°.求:
(1)直线AB的方程;
(2)直线AC和BC的方程.
分层练习-基础
解 (1)因为A(1,1),B(5,1),所以直线AB平行于x轴,所以直线AB的方程为y=1.
(2)由题意知,直线AC的倾斜角为∠A=45°,所以kAC=tan 45°=1.
又直线AC过点A(1,1),所以直线AC的方程为y-1=1×(x-1),即y=x.
同理可知,直线BC的倾斜角为180°-∠B=135°,所以kBC=tan 135°=-1.
又直线BC过点B(5,1),所以直线BC的方程为y-1=-1×(x-5),即y=-x+6.
分层练习-基础
分层练习-巩固
9.已知直线l不经过第三象限,设它的斜率为k,在y轴上的截距为b(b≠0),则( )
A.kb<0 B.kb≤0
C.kb>0 D.kb≥0
答案 B
解析 当k≠0时,∵直线l不经过第三象限,∴k<0,b>0,∴kb<0.
当k=0,b>0时,直线l也不过第三象限,∴kb≤0.
分层练习-巩固
答案 BC
分层练习-巩固
分层练习-巩固
分层练习-拓展
分层练习-拓展
12.已知直线l:y=kx+2k+1.
(1)求证:直线l恒过一个定点;
(2)当-3
由直线方程的点斜式可知,直线恒过定点(-2,1).
(2)解 设函数f(x)=kx+2k+1,显然其图象是一条直线(如图所示),
1、直线的点斜式方程
2、直线的斜截式方程
3、直线的点斜式方程和斜截式方程之间的关系
斜截式是点斜式的特殊情况,两者均不能表示斜率不存在即与x轴垂直的直线。
课堂小结
