苏教版高中数学选择性必修第一册第1章直线与方程1.4两条直线的交点课件(共67张PPT)
文档属性
| 名称 | 苏教版高中数学选择性必修第一册第1章直线与方程1.4两条直线的交点课件(共67张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 17:40:40 | ||
图片预览











文档简介
(共67张PPT)
苏教版2019高二数学(选修一)第一章 直线与方程
1.4 两条直线的交点
学习目标
1.会用解方程组的方法求两条相交直线的交点坐标.
2.会根据方程组解的个数判定两条直线的位置关系.
情景导入
在平面几何中,我们对直线做了定性研究,引入平面直角坐标系后,我们用二元一次方程表示直线,直线的方程就是相应直线上每一点的坐标所满足的一个关系式,这样我们可以通过方程把握直线上的点,进而用代数方法对直线进行定量研究,例如求两条直线的交点,坐标平面内与点、直线相关的距离问题等.
O
x
y
B
O
x
y
B
1.两条直线的交点
新知探究
直线x+y-2=0与直线x-y+3=0的位置关系是什么?
垂直
垂足的坐标能否求出?如何求呢?
(1)已知一条直线的方程如何判断一个点是否在直线上?
将点代入直线,成立则点在直线上,不成立则点不在直线上
(4)请试着总结求两条直线交点的一般方法.
答:将两条直线的方程联立,即可求出同时在两条直线上的点的座标
两条直线的交点
概念归纳
2.两直线的交点和方程组解的个数问题
新知探究
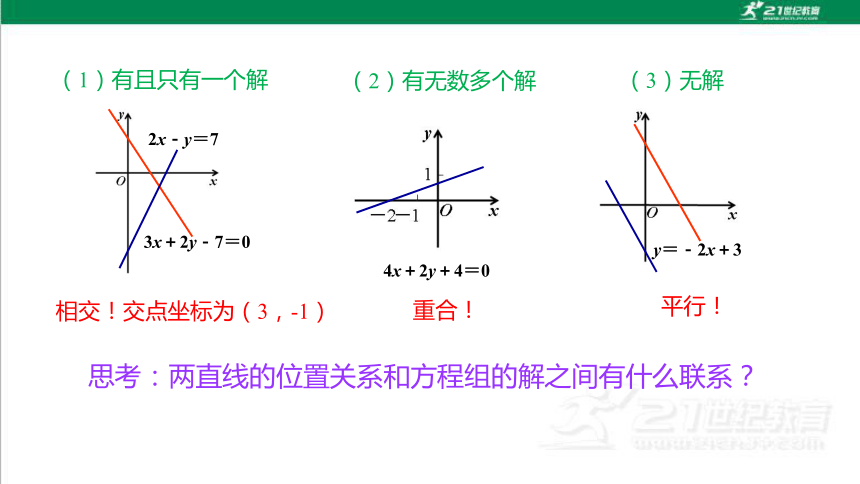
例1、解下列方程组,并分别在同一坐标系中画出每一方程组中的两条直线,观察它们的位置关系
3x+2y-7=0
2x-y=7
y=-2x+3
4x+2y+4=0
(3)无解
(1)有且只有一个解
(2)有无数多个解
平行!
重合!
相交!交点坐标为(3,-1)
思考:两直线的位置关系和方程组的解之间有什么联系?
两条直线的位置与相应方程组的解的个数之间的关系
一组
一个
相交
无数组
无数个
重 合
无解
零个
平行
概念归纳
注意点:
(1)虽然利用方程组解的个数可以判断两直线的位置关系,但是由于运算量较大,一般较少使用.
(2)两条直线相交的等价条件是A1B2-A2B1≠0.
概念归纳
3.有关直线系方程
1.直线5x+4y-2m-1=0与直线2x+3y-m=0的交点在第四象限,求m的取值范围.
【思路探究】 先求出两直线的交点,根据第四象限点的特点,横坐标为正、纵坐标为负,解不等式组求出字母m的取值范围.
典例剖析
1.直线5x+4y-2m-1=0与直线2x+3y-m=0的交
点在第四象限,求m的取值范围.
4、纳税制度
新知探究
纳税是每个公民应尽的义务和责任,市场交易时购买者同样也纳税。
例如:我们以100元的价格买入一件商品,那么其中有5元是我们所纳的税额,因此供应方得到了
100-5=95元
5、政府补贴
新知探究
政府补贴就是国家为了调节市场的供应量和需求量的比例而拿出一部分资金对市场进行宏观调控的一种手段。
例如:我们每天必须的食盐,如果我们从市场上购得食盐的价格为2元/斤,那么销售方除了我们付的2元之外,还将从国家那里得到大约0.5元的政府补贴,即供应方得到了
2+0.5=2.5元
课本例1 分别判断下列直线l1与l2是否相交.若相交,求出它们交点的坐标:
(1)l1:2x-y=7,l2:3x+2y-7=0;
(2)l1:2x-6y+4=0,l2:4x-12y+8=0;
(3)l1:4x+2y+4=0, l2:y=-2x+3.
解 (1)因为方程组的解为
所以直线l1和l2相交,且交点坐标为(3,-1).
(2)因为方程组有无数组解,所以直线l1和l2重合.
(3)因为方程组无解,所以l1∥l2.
课本例题
典例剖析
AD
概念归纳
(1)求两直线的交点坐标可直接建立方程组求解,并可利用解的个数判断直线的位置关系.
(2)当多条直线相交于同一点时,先选两直线求交点,此点必满足其他直线.
练一练
C
典例剖析
概念归纳
练一练
1.直接法:求出两直线的交点,作为待求直线上的已知点,再根据已知条件求出待求直线的
方程.
2.待定系数法:设经过两直线l1:A1x+B1y+C1=0(A1,B1不全为0),l2:A2x+B2y+C2=0(A2,B2不全为0) 的直线方程为A1x+B1y+C1+λ(A2x+B2y+C2)=0(λ为任意实数),然后根据条件求λ.
注意该设法中直线的方程可表示除l2外所有过两直线交点的直线.
1 .求过两条直线交点的直线方程的方法
高频考点
已知两直线l1:x+2y-6=0和l2:x-2y+2=0的交点为P.求:
(1)过点P与Q(1,4)的直线方程;
(2)过点P且与直线x-3y-1=0平行的直线方程.
思路点拨 思路一(直接法):(1)先求点P坐标,再由两点式方程求直线方程;(2)由直线平行, 则斜率相等得斜率,再由点斜式求直线方程.
思路二(待定系数法):(1)设出过交点的直线方程,求出参数即可;(2)由平行关系列出关于参 数的方程,求出参数即可.
典例
典例剖析
解析 解法一(直接法):(1)由 解得 即P(2,2).
所以所求直线方程为 = ,即2x+y-6=0.
(2)由(1)知点P(2,2),因为直线x-3y-1=0的斜率为 ,
所以所求直线方程为y-2= (x-2),即x-3y+4=0.
解法二(待定系数法):(1)设过直线l1和l2交点的直线方程为x+2y-6+m(x-2y+2)=0,即(m+1)x+(2- 2m)y+(2m-6)=0①.
把(1,4)代入①,化简得3-5m=0,解得m= ,所以过点P与Q的直线方程为 x+ y- =0,即2x+y-
6=0.
(2)由(1)知过直线l1和l2交点的直线方程为(m+1)x+(2-2m)y+(2m-6)=0,则由两直线平行,得-3(m
+1)=2-2m,得m=-5,所以所求直线的方程为-4x+12y-16=0,即x-3y+4=0.
1.将直线方程转化为y-y0=k(x-x0)的形式,则直线必过定点(x0,y0).
2.应用分离参数的方法,将直线方程转化为a1x+b1y+c1+λ(a2x+b2y+c2)=0,由 求
出定点坐标.
3.应用特殊值法,给方程中的参数赋两个特殊值,可得关于x,y的两个方程,将其联立并求解, 则解出的x,y的值分别为所求定点的横、纵坐标.
2.求解直线过定点问题的常用方法
方法技巧
已知(k+1)x-(k-1)y-2k=0为直线l的方程,求证:无论k取何实数,直线l都过定点,并求出这 个定点的坐标.
解析 解法一: 原方程整理得(x+y)+k(x-y-2)=0,无论k取何实数,直线l都过定点,且定点坐标 即为方程组 的解,解此方程组得
∴无论k取何实数,直线l都过定点(1,-1).
解法二:由直线l的方程得(k+1)x=(k-1)y+2k,变形为(k+1)x-(k+1)=(k-1)y+(k-1),即(k+1)(x-1)+(1- k)(y+1)=0.
直线l的方程为过定点(x0,y0)的直线系方程A(x-x0)+B(y-y0)=0的形式,所以直线l必过定点,定点 坐标为方程组 的解,解此方程组得
∴无论k取何实数,直线l都过定点(1,-1).
典例
典例剖析
解法三: 对于方程(k+1)x-(k-1)y-2k=0,令k=0,得x+y=0;令k=1,得2x-2=0.
解方程组 得 即两直线的交点为(1,-1).将(1,-1)代入已知直线方程的左边,得
(k+1)-(k-1)·(-1)-2k=0.这表明无论k取何实数,直线l都过定点(1,-1).
随堂练
随堂练
随堂练
随堂练
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
C
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-拓展
BCD
分层练习-拓展
分层练习-拓展
分层练习-拓展
两条直线的交点
课堂小结
两条直线的位置与相应方程组的解的个数之间的关系
一组
一个
相交
无数组
无数个
重 合
无解
零个
平行
课堂小结
有关直线系方程
课堂小结
课堂小结
苏教版2019高二数学(选修一)第一章 直线与方程
1.4 两条直线的交点
学习目标
1.会用解方程组的方法求两条相交直线的交点坐标.
2.会根据方程组解的个数判定两条直线的位置关系.
情景导入
在平面几何中,我们对直线做了定性研究,引入平面直角坐标系后,我们用二元一次方程表示直线,直线的方程就是相应直线上每一点的坐标所满足的一个关系式,这样我们可以通过方程把握直线上的点,进而用代数方法对直线进行定量研究,例如求两条直线的交点,坐标平面内与点、直线相关的距离问题等.
O
x
y
B
O
x
y
B
1.两条直线的交点
新知探究
直线x+y-2=0与直线x-y+3=0的位置关系是什么?
垂直
垂足的坐标能否求出?如何求呢?
(1)已知一条直线的方程如何判断一个点是否在直线上?
将点代入直线,成立则点在直线上,不成立则点不在直线上
(4)请试着总结求两条直线交点的一般方法.
答:将两条直线的方程联立,即可求出同时在两条直线上的点的座标
两条直线的交点
概念归纳
2.两直线的交点和方程组解的个数问题
新知探究
例1、解下列方程组,并分别在同一坐标系中画出每一方程组中的两条直线,观察它们的位置关系
3x+2y-7=0
2x-y=7
y=-2x+3
4x+2y+4=0
(3)无解
(1)有且只有一个解
(2)有无数多个解
平行!
重合!
相交!交点坐标为(3,-1)
思考:两直线的位置关系和方程组的解之间有什么联系?
两条直线的位置与相应方程组的解的个数之间的关系
一组
一个
相交
无数组
无数个
重 合
无解
零个
平行
概念归纳
注意点:
(1)虽然利用方程组解的个数可以判断两直线的位置关系,但是由于运算量较大,一般较少使用.
(2)两条直线相交的等价条件是A1B2-A2B1≠0.
概念归纳
3.有关直线系方程
1.直线5x+4y-2m-1=0与直线2x+3y-m=0的交点在第四象限,求m的取值范围.
【思路探究】 先求出两直线的交点,根据第四象限点的特点,横坐标为正、纵坐标为负,解不等式组求出字母m的取值范围.
典例剖析
1.直线5x+4y-2m-1=0与直线2x+3y-m=0的交
点在第四象限,求m的取值范围.
4、纳税制度
新知探究
纳税是每个公民应尽的义务和责任,市场交易时购买者同样也纳税。
例如:我们以100元的价格买入一件商品,那么其中有5元是我们所纳的税额,因此供应方得到了
100-5=95元
5、政府补贴
新知探究
政府补贴就是国家为了调节市场的供应量和需求量的比例而拿出一部分资金对市场进行宏观调控的一种手段。
例如:我们每天必须的食盐,如果我们从市场上购得食盐的价格为2元/斤,那么销售方除了我们付的2元之外,还将从国家那里得到大约0.5元的政府补贴,即供应方得到了
2+0.5=2.5元
课本例1 分别判断下列直线l1与l2是否相交.若相交,求出它们交点的坐标:
(1)l1:2x-y=7,l2:3x+2y-7=0;
(2)l1:2x-6y+4=0,l2:4x-12y+8=0;
(3)l1:4x+2y+4=0, l2:y=-2x+3.
解 (1)因为方程组的解为
所以直线l1和l2相交,且交点坐标为(3,-1).
(2)因为方程组有无数组解,所以直线l1和l2重合.
(3)因为方程组无解,所以l1∥l2.
课本例题
典例剖析
AD
概念归纳
(1)求两直线的交点坐标可直接建立方程组求解,并可利用解的个数判断直线的位置关系.
(2)当多条直线相交于同一点时,先选两直线求交点,此点必满足其他直线.
练一练
C
典例剖析
概念归纳
练一练
1.直接法:求出两直线的交点,作为待求直线上的已知点,再根据已知条件求出待求直线的
方程.
2.待定系数法:设经过两直线l1:A1x+B1y+C1=0(A1,B1不全为0),l2:A2x+B2y+C2=0(A2,B2不全为0) 的直线方程为A1x+B1y+C1+λ(A2x+B2y+C2)=0(λ为任意实数),然后根据条件求λ.
注意该设法中直线的方程可表示除l2外所有过两直线交点的直线.
1 .求过两条直线交点的直线方程的方法
高频考点
已知两直线l1:x+2y-6=0和l2:x-2y+2=0的交点为P.求:
(1)过点P与Q(1,4)的直线方程;
(2)过点P且与直线x-3y-1=0平行的直线方程.
思路点拨 思路一(直接法):(1)先求点P坐标,再由两点式方程求直线方程;(2)由直线平行, 则斜率相等得斜率,再由点斜式求直线方程.
思路二(待定系数法):(1)设出过交点的直线方程,求出参数即可;(2)由平行关系列出关于参 数的方程,求出参数即可.
典例
典例剖析
解析 解法一(直接法):(1)由 解得 即P(2,2).
所以所求直线方程为 = ,即2x+y-6=0.
(2)由(1)知点P(2,2),因为直线x-3y-1=0的斜率为 ,
所以所求直线方程为y-2= (x-2),即x-3y+4=0.
解法二(待定系数法):(1)设过直线l1和l2交点的直线方程为x+2y-6+m(x-2y+2)=0,即(m+1)x+(2- 2m)y+(2m-6)=0①.
把(1,4)代入①,化简得3-5m=0,解得m= ,所以过点P与Q的直线方程为 x+ y- =0,即2x+y-
6=0.
(2)由(1)知过直线l1和l2交点的直线方程为(m+1)x+(2-2m)y+(2m-6)=0,则由两直线平行,得-3(m
+1)=2-2m,得m=-5,所以所求直线的方程为-4x+12y-16=0,即x-3y+4=0.
1.将直线方程转化为y-y0=k(x-x0)的形式,则直线必过定点(x0,y0).
2.应用分离参数的方法,将直线方程转化为a1x+b1y+c1+λ(a2x+b2y+c2)=0,由 求
出定点坐标.
3.应用特殊值法,给方程中的参数赋两个特殊值,可得关于x,y的两个方程,将其联立并求解, 则解出的x,y的值分别为所求定点的横、纵坐标.
2.求解直线过定点问题的常用方法
方法技巧
已知(k+1)x-(k-1)y-2k=0为直线l的方程,求证:无论k取何实数,直线l都过定点,并求出这 个定点的坐标.
解析 解法一: 原方程整理得(x+y)+k(x-y-2)=0,无论k取何实数,直线l都过定点,且定点坐标 即为方程组 的解,解此方程组得
∴无论k取何实数,直线l都过定点(1,-1).
解法二:由直线l的方程得(k+1)x=(k-1)y+2k,变形为(k+1)x-(k+1)=(k-1)y+(k-1),即(k+1)(x-1)+(1- k)(y+1)=0.
直线l的方程为过定点(x0,y0)的直线系方程A(x-x0)+B(y-y0)=0的形式,所以直线l必过定点,定点 坐标为方程组 的解,解此方程组得
∴无论k取何实数,直线l都过定点(1,-1).
典例
典例剖析
解法三: 对于方程(k+1)x-(k-1)y-2k=0,令k=0,得x+y=0;令k=1,得2x-2=0.
解方程组 得 即两直线的交点为(1,-1).将(1,-1)代入已知直线方程的左边,得
(k+1)-(k-1)·(-1)-2k=0.这表明无论k取何实数,直线l都过定点(1,-1).
随堂练
随堂练
随堂练
随堂练
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
C
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-拓展
BCD
分层练习-拓展
分层练习-拓展
分层练习-拓展
两条直线的交点
课堂小结
两条直线的位置与相应方程组的解的个数之间的关系
一组
一个
相交
无数组
无数个
重 合
无解
零个
平行
课堂小结
有关直线系方程
课堂小结
课堂小结
