苏教版高中数学选择性必修第一册第1章直线与方程1.1直线的斜率与倾斜角课件(共71张PPT)
文档属性
| 名称 | 苏教版高中数学选择性必修第一册第1章直线与方程1.1直线的斜率与倾斜角课件(共71张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 5.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 17:41:03 | ||
图片预览







文档简介
(共71张PPT)
苏教版2019高二数学(选修一)第一章 直线与方程
1.1 直线的斜率与倾斜角
学习目标
1.了解直线的斜率和倾斜角的概念.
2.理解直线倾斜角的唯一性及直线斜率的存在性.
3.了解斜率公式的推导过程,会应用斜率公式求直线的斜率.
现实世界中,到处有美妙的曲线,从飞逝的流星到雨后的彩虹,从古代的石拱桥到现代的立交桥…
行星围绕太阳运行,人们可以建立行星运动的轨迹方程,并借助方程进一步认识它的运动规律.
在建造桥梁时,我们可以根据要求,首先确定桥拱所对应的曲线的方程,然后进行进一步的设计和施工.
情景导入
y
x
o
x
y
o
1.直线的斜率
新知探究
问题1:过一点有多少条直线?确定一条直线需要几个点?
(1)过一个点有 直线;
(2) 确定一条直线。
无数条
两点
问题2:确定一条直线的要素除了两点之外,还有哪些确定直线的方法?
一点与直线的方向,即直线的倾斜程度。
问题3:生活中我们如何刻画楼梯或路面的倾斜程度
楼梯或路面的倾斜程度用坡度来刻画。坡度越大道路越陡峭,坡度越小道路越平坦.
x
y
o
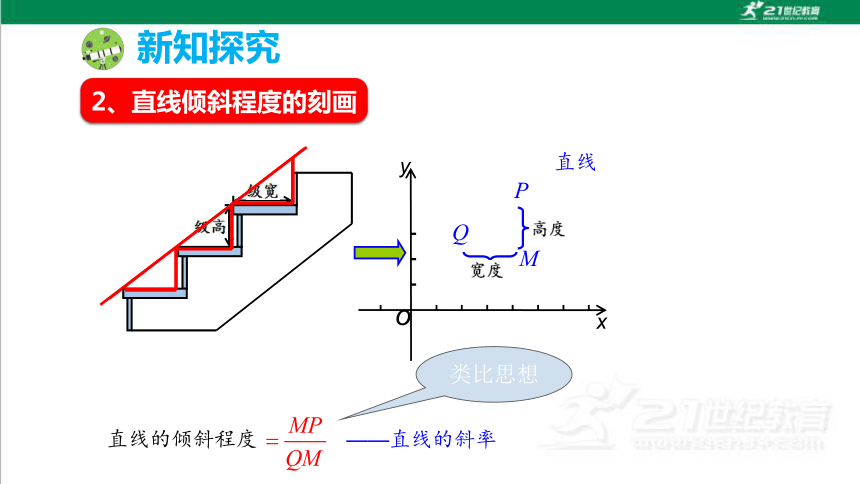
直线
类比思想
——直线的斜率
直线的倾斜程度
2、直线倾斜程度的刻画
新知探究
x
y
o
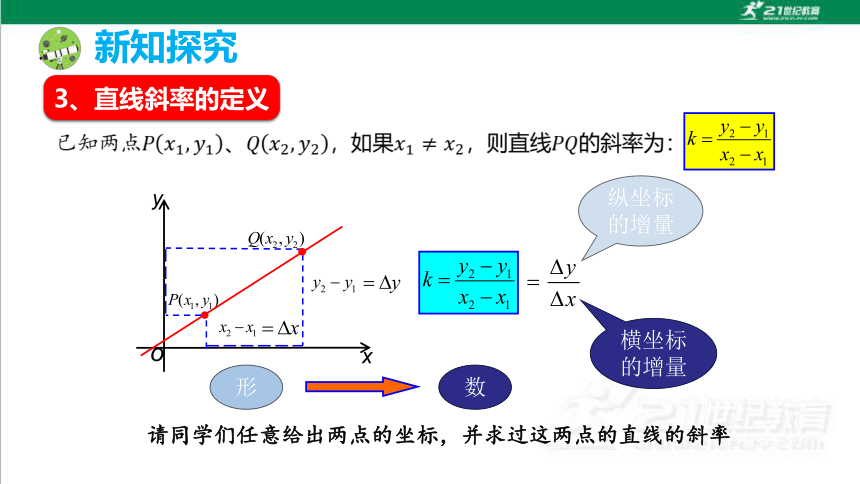
3、直线斜率的定义
新知探究
纵坐标的增量
横坐标的增量
形
数
请同学们任意给出两点的坐标,并求过这两点的直线的斜率
x
y
o
斜率不存在,这时直线PQ⊥x轴。
问题5:对于一条与x轴不垂直的定直线而言,直线的斜率是定值吗?
是定值,直线上任意两点确定的斜率总相等。
问题6:求一条直线的斜率需要什么条件?
只需知道直线上任意两点的坐标。
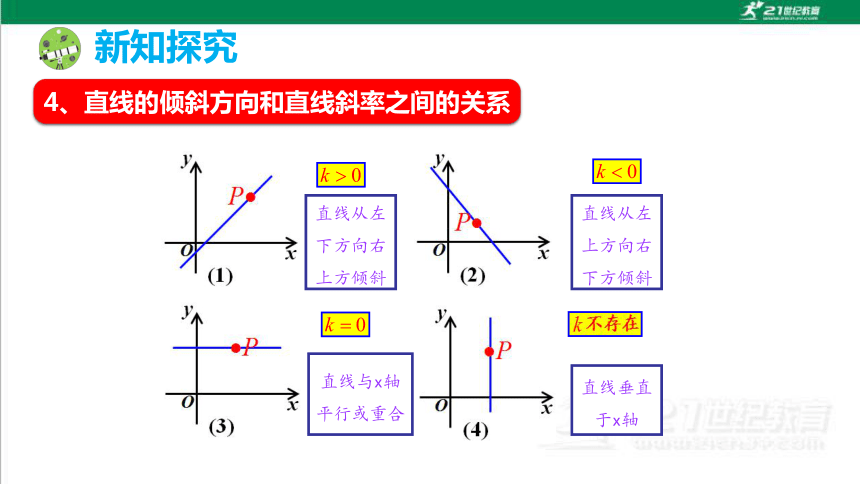
4、直线的倾斜方向和直线斜率之间的关系
新知探究
直线从左下方向右上方倾斜
直线从左上方向右下方倾斜
直线与x轴平行或重合
直线垂直于x轴
课本例1 如图所示,直线l1,l2,l3都经过点P(3,2),又l1,l2,l3分别经过点Q1(-2,-1),Q2(4,-2),Q3(-3,2).
(1)试计算直线l1,l2,l3的斜率;
(2)若还存点Q4(a,3),试求直线PQ4的斜率.
类型一 求过两点直线的斜率
典例剖析
1.已知直线l经过点A(m,2),B(1,m2+2),试求直线l的斜率。
解:当m≠1时,
当m=1时,直线AB垂直于x轴,所以斜率不存在。
练一练
2.求过点M(0,2),N(2,3m2+12m+13)(m∈R)的求直线l的斜率k的取值范围。
练一练
例2、经过点A(3,2)画直线,使直线的斜率分别为
类型二 作过定点和已知斜率的直线
典例剖析
分析,要画出直线,只需再确定直线上另一个点的位置
例2、经过点A(3,2)画直线,使直线的斜率分别为
类型二 作过定点和已知斜率的直线
典例剖析
分析,要画出直线,只需再确定直线上另一个点的位置
例3、已知三点A(-3,-3), B(-1,1), C(2,7),试求kAB和kBC 。
解:
思考:如果kAB=kBC,那么A、B、C三点有怎样的关系?有什么用处?
斜率可用来判定三点共线
类型三 利用斜率求解三点共线问题
典例剖析
1.已知三点A(a,2),B(3,7),C(-2,-9a)在一条直线上,求实数a的值。
练一练
斜率为2
问题9:平行直线的斜率之间有怎样的关系?
斜率相等或斜率都不存在
斜率为2
1、判断下列三点是否在同一直线上
(1) A(0,2), B(2,5),C(3,7);
(2) A(-1,4),B(2,1),C(-2,5)。
练一练
2、若三点A(2,3),B(a,4),C(8,a)共线,则实数a的值
为________
3、已知点A(-1,1),B(x,2),C(-2 ,y)为直线l上的三
点,若直线l的斜率为2,则x= _____, y= _____
4、直线l的斜率为2,将直线l向左平移1个单位得到直线l1,
则l1的斜率为_________
0或5
-1
2
练一练
问题10:
既然垂直于x轴的直线,斜率不存在,我们用什么
来反映这类直线的倾斜程度呢?在平面直角坐标
系中,任何一条直线与x轴都有一个相对的倾斜程
度,可以用一个什么几何量来反映一条直线与x轴
的倾斜程度?
x
y
o
5.直线倾斜角的定义
新知探究
直线倾斜角的定义
在平面直角坐标系中,对于一条与x轴相交的直线l,把 x轴所在的直线绕着交点按逆时针方向旋转到和直线l重合时所转过的最小正角称为直线l的倾斜角。
x
y
o
注意:
(1)直线向上方向;
(2)x轴的正方向。
概括:
倾斜角和斜率都是刻画直线倾斜程度的量,斜率侧重于数量关系,而倾斜角则更加直观形象。
倾斜角
下列四图中,表示直线的倾斜角的是( )
A
练一练
问题11:如果一条直线绕着一点旋转,则它的倾斜角有什么变化?取值范围是什么?
x
y
o
规定:
当直线l与x轴平行或
重合时,它的倾斜角
为0o。
6.直线倾斜角的取值范围
新知探究
问题12:任何一条直线都有倾斜角吗?不同的直线其倾斜角一定不相同吗?
2、直线倾斜角的取值范围
注意:倾斜角的范围包括0,但不包括π
你认为下列说法对吗?
(1)所有的直线都有唯一确定的倾斜角与它对应;
(2)每一个倾斜角都对应于唯一的一条直线。
思考:倾斜角与斜率有怎样的关系呢?
练一练
x
y
O
x
y
O
问题14:上述两条直线的倾斜角分别与x的系数有什么关系?
7.直线斜率的定义二
新知探究
3、直线斜率的定义二
我们把一条直线的倾斜角α的正切值叫做这条直线的斜率。
k
O
常用小写字母k表示,即
问题15:任何一条直线都有斜率吗?
结论:
任何一条直线都有倾斜角,但不是任何一条直线都存在斜率;如与x轴垂直的直线。
问题17:当直线的倾斜角α=120°,135°,150°时,则直线的斜率分别等于多少?
问题18:倾斜角为锐角、钝角或直角时,直线的斜率的取值范围分别是什么?
问题19:直线的斜率的取值范围是什么?
问题20:斜率相等的直线其倾斜角相等吗?斜率大的直线其倾斜角也大吗?
倾斜角为0° 时,k =0;
倾斜角为锐角时,k>0;
倾斜角为钝角时,k<0;
倾斜角为直角时,k不存在。
8.直线的倾斜角和斜率的关系
新知探究
例1.判断下列命题的真假:
(1)若直线的倾斜角为α,则直线的斜率为tan α;
(2)若直线的斜率为tan α,则直线的倾斜角为α;
(3)若直线的倾斜角为α,则sinα≥0;
(4)直线的斜率的范围是(-∞,+∞);
(5)因为任一条直线都有倾斜角,所以任一条直线都有
斜率;
(6)直线的倾斜角越大,则直线的斜率越大;
(7)两直线的倾斜角相等,则它们的斜率也相等;
(8)平行于x轴的直线的倾斜角是0或π。
典例剖析
类型一 直线的倾斜角和斜率的概念
x
y
O
已知直线l1,l2,l3如图所示, 则l1,l2,l3的斜率k1,k2,k3
的大小关系为_______________ ,倾斜角α1,α2,α3的大小
关系为_______________
练一练
例2、 (1)经过两点A(2,3),B(1,4) 的直线的斜率为_____,
倾斜角为________
(2)经过两点A(4,2y+1),B(2,-3) 的直线的倾斜角
为120o,则y= ________
典例剖析
类型二 直线斜率的计算
已知M(2m+3,m),N(m-2,1),
(1)当m为何值时,直线MN的倾斜角为锐角?
(2)当m为何值时,直线MN的倾斜角为钝角?
(3)当m为何值时,直线MN的倾斜角为直角?
练一练
例3、已知直线l1的倾斜角α1=15o,直线l1和l2的交点A,直
线l1绕点A按顺时针方向旋转到与直线l2重合时所转
的最小正角为60o,求直线l2的斜率k。
典例剖析
类型三 两直线倾斜角的关系
例4、若一条直线的倾斜角范围为 ,求这条直线斜率k的取值范围。
典例剖析
类型四 直线的倾斜角和斜率关系的综合应用
1、若一条直线的倾斜角范围为 ,则
这条直线斜率k的取值范围为_______________
练一练
2、若一条直线的斜率的范围为 ,则这条直线倾斜
角α的取值范围为_______________
练一练
例5、若过原点O的直线l与连结P(2,2),Q(6, )的线段相交,求直线 l 的倾斜角和斜率的取值范围。
x
y
o
典例剖析
类型四 直线的倾斜角和斜率关系的综合应用
1.(多选)下列说法正确的是( )
A.若α是直线l的倾斜角,则0°≤α<180°
B.若k是直线的斜率,则k∈R
C.任意一条直线都有倾斜角,但不一定有斜率
D.任意一条直线都有斜率,但不一定有倾斜角
答案 ABC
2.若经过A(m,3),B(1,2)两点的直线的倾斜角为45°,则m等于( )
A.2 B.1 C.-1 D.-2
答案 A
随堂练
解析 由题意知tan 45°= ,解得m=2.
随堂练
4.经过A(m,3),B(1,2)两点的直线的倾斜角α的取值范围是________.(其中m≥1)
答案 0°<α≤90°
随堂练
课本练习
1.分别求经过下列两点的直线的斜率:
(1)(2,3),(4,5);
(2)(-2,3),(2,1);
(3)(-3,-1),(2,-1);
(4)(1,0),(0,-2).
课本练习
课本练习
课本练习
课本练习
课本练习
(1)P(1,2),k=3;可得直线方程为:y-2=3(x-1),
课本练习
(3)P(-1,3),k= 0;可得直线方程为:y = 3.
(4)P(-2,0),斜率不存在.可得直线方程为:x=-2.
课本练习
5,分别判断下列三点是否在同一直线上:
(1)(0,2),(2,5),(3,7);
(2)(-1,4),(2,1),(-2,5);
(3)(1,2),(1,3),(1,-1).
课本练习
易错点:倾斜角和斜率的关系及其应用
当直线l的倾斜角α∈ 时,k≥0,且α越大,斜率k越大;当直线l的倾斜角α∈ 时,
k<0,且α越大,斜率k越大;当直线l的倾斜角α= 时,它的斜率不存在.k=tan α 的
图象如图所示.
由斜率k的范围截取函数图象,可得到倾斜角α的范围;反过来,
由倾斜角α的范围截取函数图象,可得到斜率k的范围.
错因分析
已知两点A(-3,4),B(3,2),过点P(1,0)的直线l与线段AB有公共点.
(1)求直线l的斜率k的取值范围;
(2)求直线l的倾斜角α的取值范围.
思路点拨:作出图形并观察,可以发现当直线l的倾斜角α介于直线PB与PA的倾斜角之间 (包括直线PB与PA的倾斜角)时,直线l与线段AB有公共点.
错因分析
解析 如图,由题意可知kPA= =-1,kPB= =1.
(1)要使直线l与线段AB有公共点,则直线l的斜率k的取值范围是k≤-1或k≥1.
(2)由图可知,直线l的倾斜角α应介于直线PB与PA的倾斜角之间(包括直线PB
与PA的倾斜角),
易知直线PB的倾斜角是 ,直线PA的倾斜角是 ,
∴直线l的倾斜角α的取值范围是 ≤α≤ .
错因分析
易错警示 本题易错误地认为斜率k的取值范围是-1≤k≤1,
结合图形考虑,l的倾斜角α应介于直线PB与直线PA的倾斜角之
间(包括直线PB与PA的倾斜角),即 ≤α≤ ,利用k=tan α
(0≤α<π)的图象(如图所示)得到k的取值范围是k≤-1或k≥1.
错因分析
分层练习-基础
A
A
分层练习-基础
C
B
分层练习-基础
6
-3
(1)已知三点A(a,2),B(5,1),C(-4,2a)在同一直线上,则a= ( )
A.2或 B.2
C. D.-2
(2)已知正△ABC的顶点A(1,1),B(1,3),点C在第一象限,若点P(x,y)是△ABC内部及其边界上 一点,则 的最大值为 ( )
A. B.
C. D.
A
B
分层练习-巩固
直线斜率的应用
解析 (1)由题意可得kBC=kAB,即 = ,解得a=2或a= .故选A.
(2)在平面直角坐标系中画出正△ABC,可知顶点C的坐标为(1+ ,2), 可看作△ABC内
部及其边界上一点P(x,y)与点(-1,0)连线的斜率,
当点P运动到点B时,直线的斜率最大,故 的最大值为 = .故选B.
分层练习-巩固
1.如下图,已知A(3,2),B(-4,1),
C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角。
分层练习-巩固
评:已知直线上一个点和直线的斜率作直线的基本步骤:
(1)根据已知的斜率由斜率公式在直线上另外再找 一个点(不唯一)
(2)由两点确定唯一的直线把所求的直线作出来.
分层练习-巩固
-1
分层练习-巩固
分层练习-巩固
分层练习-拓展
解析 作出函数f(x)=log3(x+2)的大致图象,如图所示.
分层练习-拓展
分层练习-拓展
2、直线斜率的两个定义
3、直线倾斜角和斜率的取值范围
1、直线倾斜角的定义
在平面直角坐标系中,对于一条与x轴相交的直线l,把 x轴所在的直线绕着交点按逆时针方向旋转到和直线l重合时所转过的最小正角称为直线l的倾斜角。
注意:(1)直线向上方向; (2)x轴的正方向。
课堂小结
4、直线的倾斜方向和直线斜率之间的关系
课堂小结
直线从左下方向右上方倾斜
直线从左上方向右下方倾斜
直线与x轴平行或重合
直线垂直于x轴
5、直线倾斜角和斜率的关系
课堂小结
苏教版2019高二数学(选修一)第一章 直线与方程
1.1 直线的斜率与倾斜角
学习目标
1.了解直线的斜率和倾斜角的概念.
2.理解直线倾斜角的唯一性及直线斜率的存在性.
3.了解斜率公式的推导过程,会应用斜率公式求直线的斜率.
现实世界中,到处有美妙的曲线,从飞逝的流星到雨后的彩虹,从古代的石拱桥到现代的立交桥…
行星围绕太阳运行,人们可以建立行星运动的轨迹方程,并借助方程进一步认识它的运动规律.
在建造桥梁时,我们可以根据要求,首先确定桥拱所对应的曲线的方程,然后进行进一步的设计和施工.
情景导入
y
x
o
x
y
o
1.直线的斜率
新知探究
问题1:过一点有多少条直线?确定一条直线需要几个点?
(1)过一个点有 直线;
(2) 确定一条直线。
无数条
两点
问题2:确定一条直线的要素除了两点之外,还有哪些确定直线的方法?
一点与直线的方向,即直线的倾斜程度。
问题3:生活中我们如何刻画楼梯或路面的倾斜程度
楼梯或路面的倾斜程度用坡度来刻画。坡度越大道路越陡峭,坡度越小道路越平坦.
x
y
o
直线
类比思想
——直线的斜率
直线的倾斜程度
2、直线倾斜程度的刻画
新知探究
x
y
o
3、直线斜率的定义
新知探究
纵坐标的增量
横坐标的增量
形
数
请同学们任意给出两点的坐标,并求过这两点的直线的斜率
x
y
o
斜率不存在,这时直线PQ⊥x轴。
问题5:对于一条与x轴不垂直的定直线而言,直线的斜率是定值吗?
是定值,直线上任意两点确定的斜率总相等。
问题6:求一条直线的斜率需要什么条件?
只需知道直线上任意两点的坐标。
4、直线的倾斜方向和直线斜率之间的关系
新知探究
直线从左下方向右上方倾斜
直线从左上方向右下方倾斜
直线与x轴平行或重合
直线垂直于x轴
课本例1 如图所示,直线l1,l2,l3都经过点P(3,2),又l1,l2,l3分别经过点Q1(-2,-1),Q2(4,-2),Q3(-3,2).
(1)试计算直线l1,l2,l3的斜率;
(2)若还存点Q4(a,3),试求直线PQ4的斜率.
类型一 求过两点直线的斜率
典例剖析
1.已知直线l经过点A(m,2),B(1,m2+2),试求直线l的斜率。
解:当m≠1时,
当m=1时,直线AB垂直于x轴,所以斜率不存在。
练一练
2.求过点M(0,2),N(2,3m2+12m+13)(m∈R)的求直线l的斜率k的取值范围。
练一练
例2、经过点A(3,2)画直线,使直线的斜率分别为
类型二 作过定点和已知斜率的直线
典例剖析
分析,要画出直线,只需再确定直线上另一个点的位置
例2、经过点A(3,2)画直线,使直线的斜率分别为
类型二 作过定点和已知斜率的直线
典例剖析
分析,要画出直线,只需再确定直线上另一个点的位置
例3、已知三点A(-3,-3), B(-1,1), C(2,7),试求kAB和kBC 。
解:
思考:如果kAB=kBC,那么A、B、C三点有怎样的关系?有什么用处?
斜率可用来判定三点共线
类型三 利用斜率求解三点共线问题
典例剖析
1.已知三点A(a,2),B(3,7),C(-2,-9a)在一条直线上,求实数a的值。
练一练
斜率为2
问题9:平行直线的斜率之间有怎样的关系?
斜率相等或斜率都不存在
斜率为2
1、判断下列三点是否在同一直线上
(1) A(0,2), B(2,5),C(3,7);
(2) A(-1,4),B(2,1),C(-2,5)。
练一练
2、若三点A(2,3),B(a,4),C(8,a)共线,则实数a的值
为________
3、已知点A(-1,1),B(x,2),C(-2 ,y)为直线l上的三
点,若直线l的斜率为2,则x= _____, y= _____
4、直线l的斜率为2,将直线l向左平移1个单位得到直线l1,
则l1的斜率为_________
0或5
-1
2
练一练
问题10:
既然垂直于x轴的直线,斜率不存在,我们用什么
来反映这类直线的倾斜程度呢?在平面直角坐标
系中,任何一条直线与x轴都有一个相对的倾斜程
度,可以用一个什么几何量来反映一条直线与x轴
的倾斜程度?
x
y
o
5.直线倾斜角的定义
新知探究
直线倾斜角的定义
在平面直角坐标系中,对于一条与x轴相交的直线l,把 x轴所在的直线绕着交点按逆时针方向旋转到和直线l重合时所转过的最小正角称为直线l的倾斜角。
x
y
o
注意:
(1)直线向上方向;
(2)x轴的正方向。
概括:
倾斜角和斜率都是刻画直线倾斜程度的量,斜率侧重于数量关系,而倾斜角则更加直观形象。
倾斜角
下列四图中,表示直线的倾斜角的是( )
A
练一练
问题11:如果一条直线绕着一点旋转,则它的倾斜角有什么变化?取值范围是什么?
x
y
o
规定:
当直线l与x轴平行或
重合时,它的倾斜角
为0o。
6.直线倾斜角的取值范围
新知探究
问题12:任何一条直线都有倾斜角吗?不同的直线其倾斜角一定不相同吗?
2、直线倾斜角的取值范围
注意:倾斜角的范围包括0,但不包括π
你认为下列说法对吗?
(1)所有的直线都有唯一确定的倾斜角与它对应;
(2)每一个倾斜角都对应于唯一的一条直线。
思考:倾斜角与斜率有怎样的关系呢?
练一练
x
y
O
x
y
O
问题14:上述两条直线的倾斜角分别与x的系数有什么关系?
7.直线斜率的定义二
新知探究
3、直线斜率的定义二
我们把一条直线的倾斜角α的正切值叫做这条直线的斜率。
k
O
常用小写字母k表示,即
问题15:任何一条直线都有斜率吗?
结论:
任何一条直线都有倾斜角,但不是任何一条直线都存在斜率;如与x轴垂直的直线。
问题17:当直线的倾斜角α=120°,135°,150°时,则直线的斜率分别等于多少?
问题18:倾斜角为锐角、钝角或直角时,直线的斜率的取值范围分别是什么?
问题19:直线的斜率的取值范围是什么?
问题20:斜率相等的直线其倾斜角相等吗?斜率大的直线其倾斜角也大吗?
倾斜角为0° 时,k =0;
倾斜角为锐角时,k>0;
倾斜角为钝角时,k<0;
倾斜角为直角时,k不存在。
8.直线的倾斜角和斜率的关系
新知探究
例1.判断下列命题的真假:
(1)若直线的倾斜角为α,则直线的斜率为tan α;
(2)若直线的斜率为tan α,则直线的倾斜角为α;
(3)若直线的倾斜角为α,则sinα≥0;
(4)直线的斜率的范围是(-∞,+∞);
(5)因为任一条直线都有倾斜角,所以任一条直线都有
斜率;
(6)直线的倾斜角越大,则直线的斜率越大;
(7)两直线的倾斜角相等,则它们的斜率也相等;
(8)平行于x轴的直线的倾斜角是0或π。
典例剖析
类型一 直线的倾斜角和斜率的概念
x
y
O
已知直线l1,l2,l3如图所示, 则l1,l2,l3的斜率k1,k2,k3
的大小关系为_______________ ,倾斜角α1,α2,α3的大小
关系为_______________
练一练
例2、 (1)经过两点A(2,3),B(1,4) 的直线的斜率为_____,
倾斜角为________
(2)经过两点A(4,2y+1),B(2,-3) 的直线的倾斜角
为120o,则y= ________
典例剖析
类型二 直线斜率的计算
已知M(2m+3,m),N(m-2,1),
(1)当m为何值时,直线MN的倾斜角为锐角?
(2)当m为何值时,直线MN的倾斜角为钝角?
(3)当m为何值时,直线MN的倾斜角为直角?
练一练
例3、已知直线l1的倾斜角α1=15o,直线l1和l2的交点A,直
线l1绕点A按顺时针方向旋转到与直线l2重合时所转
的最小正角为60o,求直线l2的斜率k。
典例剖析
类型三 两直线倾斜角的关系
例4、若一条直线的倾斜角范围为 ,求这条直线斜率k的取值范围。
典例剖析
类型四 直线的倾斜角和斜率关系的综合应用
1、若一条直线的倾斜角范围为 ,则
这条直线斜率k的取值范围为_______________
练一练
2、若一条直线的斜率的范围为 ,则这条直线倾斜
角α的取值范围为_______________
练一练
例5、若过原点O的直线l与连结P(2,2),Q(6, )的线段相交,求直线 l 的倾斜角和斜率的取值范围。
x
y
o
典例剖析
类型四 直线的倾斜角和斜率关系的综合应用
1.(多选)下列说法正确的是( )
A.若α是直线l的倾斜角,则0°≤α<180°
B.若k是直线的斜率,则k∈R
C.任意一条直线都有倾斜角,但不一定有斜率
D.任意一条直线都有斜率,但不一定有倾斜角
答案 ABC
2.若经过A(m,3),B(1,2)两点的直线的倾斜角为45°,则m等于( )
A.2 B.1 C.-1 D.-2
答案 A
随堂练
解析 由题意知tan 45°= ,解得m=2.
随堂练
4.经过A(m,3),B(1,2)两点的直线的倾斜角α的取值范围是________.(其中m≥1)
答案 0°<α≤90°
随堂练
课本练习
1.分别求经过下列两点的直线的斜率:
(1)(2,3),(4,5);
(2)(-2,3),(2,1);
(3)(-3,-1),(2,-1);
(4)(1,0),(0,-2).
课本练习
课本练习
课本练习
课本练习
课本练习
(1)P(1,2),k=3;可得直线方程为:y-2=3(x-1),
课本练习
(3)P(-1,3),k= 0;可得直线方程为:y = 3.
(4)P(-2,0),斜率不存在.可得直线方程为:x=-2.
课本练习
5,分别判断下列三点是否在同一直线上:
(1)(0,2),(2,5),(3,7);
(2)(-1,4),(2,1),(-2,5);
(3)(1,2),(1,3),(1,-1).
课本练习
易错点:倾斜角和斜率的关系及其应用
当直线l的倾斜角α∈ 时,k≥0,且α越大,斜率k越大;当直线l的倾斜角α∈ 时,
k<0,且α越大,斜率k越大;当直线l的倾斜角α= 时,它的斜率不存在.k=tan α 的
图象如图所示.
由斜率k的范围截取函数图象,可得到倾斜角α的范围;反过来,
由倾斜角α的范围截取函数图象,可得到斜率k的范围.
错因分析
已知两点A(-3,4),B(3,2),过点P(1,0)的直线l与线段AB有公共点.
(1)求直线l的斜率k的取值范围;
(2)求直线l的倾斜角α的取值范围.
思路点拨:作出图形并观察,可以发现当直线l的倾斜角α介于直线PB与PA的倾斜角之间 (包括直线PB与PA的倾斜角)时,直线l与线段AB有公共点.
错因分析
解析 如图,由题意可知kPA= =-1,kPB= =1.
(1)要使直线l与线段AB有公共点,则直线l的斜率k的取值范围是k≤-1或k≥1.
(2)由图可知,直线l的倾斜角α应介于直线PB与PA的倾斜角之间(包括直线PB
与PA的倾斜角),
易知直线PB的倾斜角是 ,直线PA的倾斜角是 ,
∴直线l的倾斜角α的取值范围是 ≤α≤ .
错因分析
易错警示 本题易错误地认为斜率k的取值范围是-1≤k≤1,
结合图形考虑,l的倾斜角α应介于直线PB与直线PA的倾斜角之
间(包括直线PB与PA的倾斜角),即 ≤α≤ ,利用k=tan α
(0≤α<π)的图象(如图所示)得到k的取值范围是k≤-1或k≥1.
错因分析
分层练习-基础
A
A
分层练习-基础
C
B
分层练习-基础
6
-3
(1)已知三点A(a,2),B(5,1),C(-4,2a)在同一直线上,则a= ( )
A.2或 B.2
C. D.-2
(2)已知正△ABC的顶点A(1,1),B(1,3),点C在第一象限,若点P(x,y)是△ABC内部及其边界上 一点,则 的最大值为 ( )
A. B.
C. D.
A
B
分层练习-巩固
直线斜率的应用
解析 (1)由题意可得kBC=kAB,即 = ,解得a=2或a= .故选A.
(2)在平面直角坐标系中画出正△ABC,可知顶点C的坐标为(1+ ,2), 可看作△ABC内
部及其边界上一点P(x,y)与点(-1,0)连线的斜率,
当点P运动到点B时,直线的斜率最大,故 的最大值为 = .故选B.
分层练习-巩固
1.如下图,已知A(3,2),B(-4,1),
C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角。
分层练习-巩固
评:已知直线上一个点和直线的斜率作直线的基本步骤:
(1)根据已知的斜率由斜率公式在直线上另外再找 一个点(不唯一)
(2)由两点确定唯一的直线把所求的直线作出来.
分层练习-巩固
-1
分层练习-巩固
分层练习-巩固
分层练习-拓展
解析 作出函数f(x)=log3(x+2)的大致图象,如图所示.
分层练习-拓展
分层练习-拓展
2、直线斜率的两个定义
3、直线倾斜角和斜率的取值范围
1、直线倾斜角的定义
在平面直角坐标系中,对于一条与x轴相交的直线l,把 x轴所在的直线绕着交点按逆时针方向旋转到和直线l重合时所转过的最小正角称为直线l的倾斜角。
注意:(1)直线向上方向; (2)x轴的正方向。
课堂小结
4、直线的倾斜方向和直线斜率之间的关系
课堂小结
直线从左下方向右上方倾斜
直线从左上方向右下方倾斜
直线与x轴平行或重合
直线垂直于x轴
5、直线倾斜角和斜率的关系
课堂小结
