苏教版高中数学选择性必修第一册第1章直线与方程1.5.2点到直线的距离 课件(共75张PPT)
文档属性
| 名称 | 苏教版高中数学选择性必修第一册第1章直线与方程1.5.2点到直线的距离 课件(共75张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 17:42:50 | ||
图片预览







文档简介
(共75张PPT)
苏教版2019高一数学(选修一)第一章 直线与方程
1.5.2 点到直线的距离
学习目标
1.会用坐标法、面积法推导点到直线的距离公式的运算过程.
2.掌握点到直线的距离公式,并能灵活应用.
5.学会点点、点线、线线对称问题.
6.会应用对称问题解决最值问题和反射问题.
3.理解两条平行直线间的距离公式的推导.
4.会求两条平行直线间的距离.
情景导入
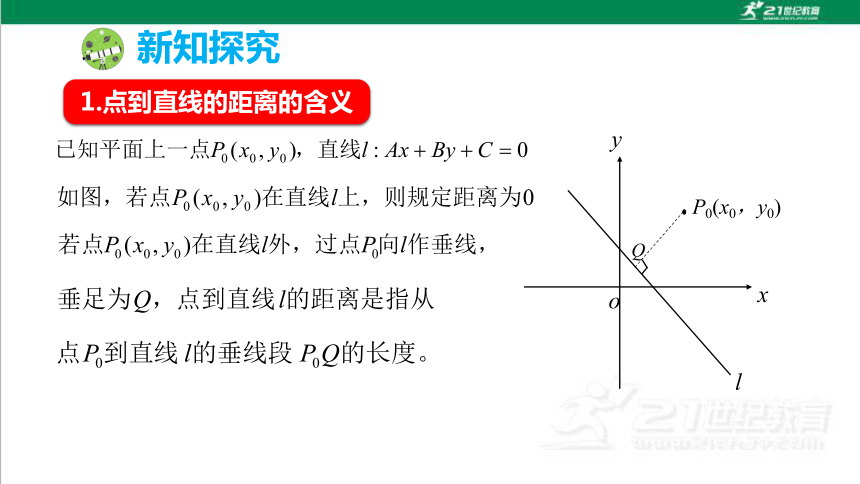
在铁路的附近,有一大型仓库,现要修建一条公路与之连接起来,易知从仓库垂直于铁路方向所修的公路最短,将铁路看作一条直线l,仓库看作点P,怎样求得仓库到铁路的最短距离呢?
1、平面内任意两点间的距离公式
已知平面内任意两点A(x1,y1)、B(x2,y2),则
2、两点的中点坐标公式
已知平面内任意两点P1(x1,y1)、P2(x2,y2),线段P1P2 的中点为 M(x0,y0),则
复习回顾
3、三角形的重心坐标公式
已知△ABC的三个顶点的坐标分别A(x1,y1)、B(x2,y2) 和C(x3,y3), 则△ABC的重心G的坐标为
即:
l
P0(x0,y0)
x
y
o
Q
1.点到直线的距离的含义
新知探究
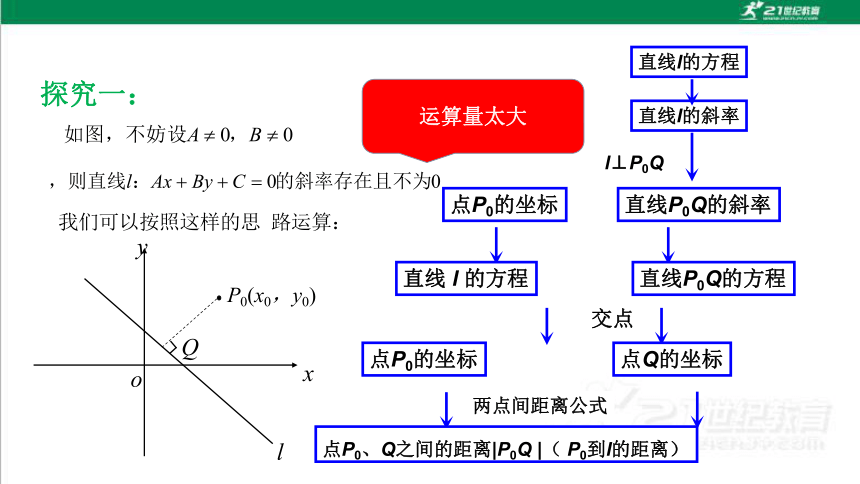
直线l的方程
直线l的斜率
直线P0Q的斜率
点P0的坐标
l⊥P0Q
直线P0Q的方程
直线 l 的方程
交点
点Q的坐标
点P0的坐标
两点间距离公式
点P0、Q之间的距离|P0Q |( P0到l的距离)
运算量太大
探究一:
l
P0(x0,y0)
x
y
o
Q
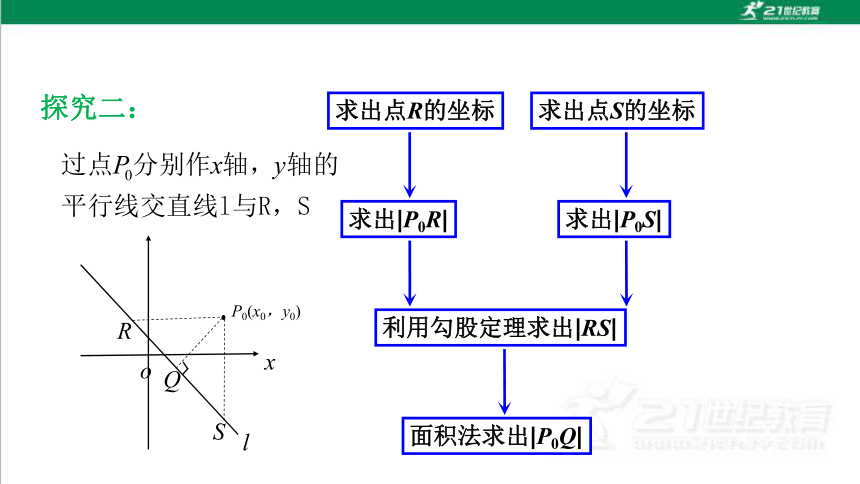
探究二:
求出点R的坐标
求出点S的坐标
求出|P0R|
求出|P0S|
利用勾股定理求出|RS|
面积法求出|P0Q|
l
P0(x0,y0)
x
o
Q
S
R
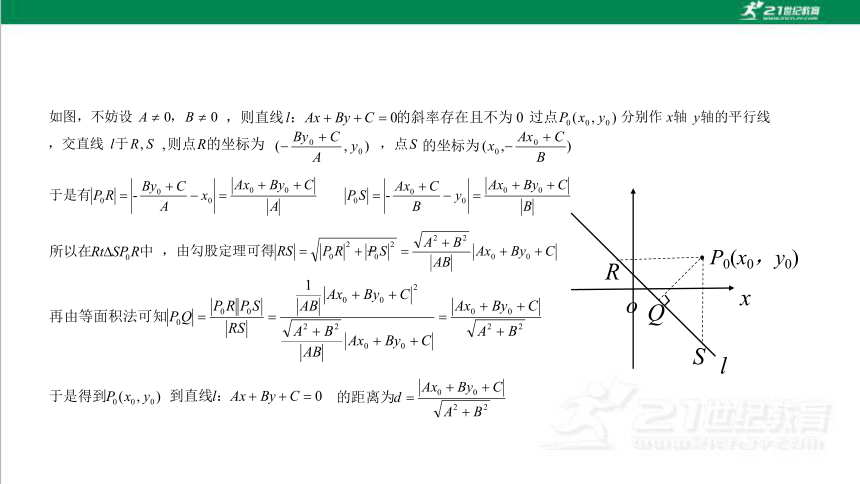
l
P0(x0,y0)
x
o
Q
S
R
l:By+C=0
P0(x0,y0)
x
y
o
Q
l:Ax+C=0
P0(x0,y0)
x
y
o
Q
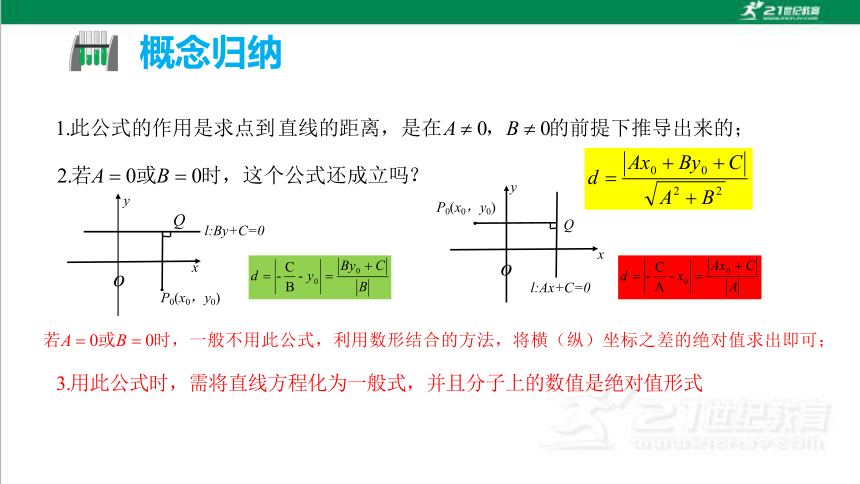
概念归纳
2.点到直线的距离公式的应用
新知探究
l1
l2
典例剖析
典例剖析
反思感悟 求点到直线的距离时,直线方程应为一般式,若给出其他形式,应先化成一般式再用公式;直线方程Ax+By+C=0(A,B不全为0)中A=0或B=0时,公式也成立,但由于直线是特殊直线(与坐标轴垂直),故也可采用数形结合法求点到直线的距离.
概念归纳
用待定系数法求直线方程时一定要讨论斜率不存在的情况
典例剖析
x
y
o
B
M(-1,2)
A
反思感悟 两点到直线的距离相等,可用几何法,即直线与两定点所在直线平行,或直线过以两定点为端点的线段的中点,此类题型也可用代数法.
概念归纳
l1
l2
Q
x
o
P0(x0,y0)
y
3.两条平行线间的距离含义
新知探究
注意点:
(1)两条平行直线间的距离:指夹在这两条平行直线间的公垂线段的长.
(2)两平行直线间的距离可以转化为点到直线的距离.
(3)运用两平行直线间的距离公式时,必须保证两直线方程中x,y的系数分别对应相同.
概念归纳
x
l1
y
o
l2
P0
Q
线线距 点线距
4.两条平行线间的距离的求法
新知探究
用此公式时,一定要注意将直线方程中x,y前的系数化为对应相同的形式!
l1
l2
Q
x
o
P(x0,y0)
y
典例剖析
先将x,y前的系数化为相同的形式,不然公式不可用
概念归纳
典例剖析
反思感悟 对于已知两直线间的距离求参数的问题,一般可列出关于距离的等式,解方程即可.
典例剖析
5.平行直线间的距离的最值问题
概念归纳
反思感悟 应用数形结合思想求最值
(1)解决此题的关键是理解式子表示的几何意义,将“数”转化为“形”,从而利用图形的直观性加以解决.
(2)数形结合、运动变化的思想方法在解题中经常用到.当图形中的元素运动变化时我们能直观观察到一些量的变化情况,进而可求出这些量的变化范围.
典例剖析
6.几类常见的对称问题
反思感悟 对称问题的解决方法
(1)点关于点的对称问题通常利用中点坐标公式.
点P(x,y)关于Q(a,b)的对称点为P′(2a-x,2b-y).
(2)直线关于点的对称直线通常用转移法或取特殊点来求.
设l的方程为Ax+By+C=0(A2+B2≠0),点P(x0,y0),
则l关于P点的对称直线方程为A(2x0-x)+B(2y0-y)+C=0.
(3)点关于直线的对称点,要抓住“垂直”和“平分”.
设P(x0,y0),l:Ax+By+C=0(A2+B2≠0),P关于l的对称点Q可以通过条件:①PQ⊥l;②PQ的中点在l上来求得.
(4)求直线关于直线的对称直线的问题可转化为点关于直线的对称问题.
概念归纳
典例剖析
7.光的反射问题
反思感悟 根据平面几何知识和光学知识,入射光线、反射光线上对应的点是关于法线对称的.利用点的对称关系可以求解.
典例剖析
8.利用对称解有关最值问题
反思感悟 利用对称性求距离的最值问题
由平面几何知识(三角形任两边之和大于第三边,任两边之差的绝对值小于第三边)可知,要解决在直线l上求一点,使这点到两定点A,B的距离之差最大的问题,应注意两点在已知直线的同侧还是异侧.
概念归纳
随堂练
随堂练
随堂练
随堂练
随堂练
随堂练
分层练习-基础
AC
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-巩固
分层练习-巩固
B
分层练习-巩固
分层练习-巩固
C
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-拓展
分层练习-拓展
分层练习-拓展
分层练习-拓展
分层练习-拓展
分层练习-拓展
分层练习-拓展
分层练习-拓展
课堂小结
苏教版2019高一数学(选修一)第一章 直线与方程
1.5.2 点到直线的距离
学习目标
1.会用坐标法、面积法推导点到直线的距离公式的运算过程.
2.掌握点到直线的距离公式,并能灵活应用.
5.学会点点、点线、线线对称问题.
6.会应用对称问题解决最值问题和反射问题.
3.理解两条平行直线间的距离公式的推导.
4.会求两条平行直线间的距离.
情景导入
在铁路的附近,有一大型仓库,现要修建一条公路与之连接起来,易知从仓库垂直于铁路方向所修的公路最短,将铁路看作一条直线l,仓库看作点P,怎样求得仓库到铁路的最短距离呢?
1、平面内任意两点间的距离公式
已知平面内任意两点A(x1,y1)、B(x2,y2),则
2、两点的中点坐标公式
已知平面内任意两点P1(x1,y1)、P2(x2,y2),线段P1P2 的中点为 M(x0,y0),则
复习回顾
3、三角形的重心坐标公式
已知△ABC的三个顶点的坐标分别A(x1,y1)、B(x2,y2) 和C(x3,y3), 则△ABC的重心G的坐标为
即:
l
P0(x0,y0)
x
y
o
Q
1.点到直线的距离的含义
新知探究
直线l的方程
直线l的斜率
直线P0Q的斜率
点P0的坐标
l⊥P0Q
直线P0Q的方程
直线 l 的方程
交点
点Q的坐标
点P0的坐标
两点间距离公式
点P0、Q之间的距离|P0Q |( P0到l的距离)
运算量太大
探究一:
l
P0(x0,y0)
x
y
o
Q
探究二:
求出点R的坐标
求出点S的坐标
求出|P0R|
求出|P0S|
利用勾股定理求出|RS|
面积法求出|P0Q|
l
P0(x0,y0)
x
o
Q
S
R
l
P0(x0,y0)
x
o
Q
S
R
l:By+C=0
P0(x0,y0)
x
y
o
Q
l:Ax+C=0
P0(x0,y0)
x
y
o
Q
概念归纳
2.点到直线的距离公式的应用
新知探究
l1
l2
典例剖析
典例剖析
反思感悟 求点到直线的距离时,直线方程应为一般式,若给出其他形式,应先化成一般式再用公式;直线方程Ax+By+C=0(A,B不全为0)中A=0或B=0时,公式也成立,但由于直线是特殊直线(与坐标轴垂直),故也可采用数形结合法求点到直线的距离.
概念归纳
用待定系数法求直线方程时一定要讨论斜率不存在的情况
典例剖析
x
y
o
B
M(-1,2)
A
反思感悟 两点到直线的距离相等,可用几何法,即直线与两定点所在直线平行,或直线过以两定点为端点的线段的中点,此类题型也可用代数法.
概念归纳
l1
l2
Q
x
o
P0(x0,y0)
y
3.两条平行线间的距离含义
新知探究
注意点:
(1)两条平行直线间的距离:指夹在这两条平行直线间的公垂线段的长.
(2)两平行直线间的距离可以转化为点到直线的距离.
(3)运用两平行直线间的距离公式时,必须保证两直线方程中x,y的系数分别对应相同.
概念归纳
x
l1
y
o
l2
P0
Q
线线距 点线距
4.两条平行线间的距离的求法
新知探究
用此公式时,一定要注意将直线方程中x,y前的系数化为对应相同的形式!
l1
l2
Q
x
o
P(x0,y0)
y
典例剖析
先将x,y前的系数化为相同的形式,不然公式不可用
概念归纳
典例剖析
反思感悟 对于已知两直线间的距离求参数的问题,一般可列出关于距离的等式,解方程即可.
典例剖析
5.平行直线间的距离的最值问题
概念归纳
反思感悟 应用数形结合思想求最值
(1)解决此题的关键是理解式子表示的几何意义,将“数”转化为“形”,从而利用图形的直观性加以解决.
(2)数形结合、运动变化的思想方法在解题中经常用到.当图形中的元素运动变化时我们能直观观察到一些量的变化情况,进而可求出这些量的变化范围.
典例剖析
6.几类常见的对称问题
反思感悟 对称问题的解决方法
(1)点关于点的对称问题通常利用中点坐标公式.
点P(x,y)关于Q(a,b)的对称点为P′(2a-x,2b-y).
(2)直线关于点的对称直线通常用转移法或取特殊点来求.
设l的方程为Ax+By+C=0(A2+B2≠0),点P(x0,y0),
则l关于P点的对称直线方程为A(2x0-x)+B(2y0-y)+C=0.
(3)点关于直线的对称点,要抓住“垂直”和“平分”.
设P(x0,y0),l:Ax+By+C=0(A2+B2≠0),P关于l的对称点Q可以通过条件:①PQ⊥l;②PQ的中点在l上来求得.
(4)求直线关于直线的对称直线的问题可转化为点关于直线的对称问题.
概念归纳
典例剖析
7.光的反射问题
反思感悟 根据平面几何知识和光学知识,入射光线、反射光线上对应的点是关于法线对称的.利用点的对称关系可以求解.
典例剖析
8.利用对称解有关最值问题
反思感悟 利用对称性求距离的最值问题
由平面几何知识(三角形任两边之和大于第三边,任两边之差的绝对值小于第三边)可知,要解决在直线l上求一点,使这点到两定点A,B的距离之差最大的问题,应注意两点在已知直线的同侧还是异侧.
概念归纳
随堂练
随堂练
随堂练
随堂练
随堂练
随堂练
分层练习-基础
AC
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-巩固
分层练习-巩固
B
分层练习-巩固
分层练习-巩固
C
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-拓展
分层练习-拓展
分层练习-拓展
分层练习-拓展
分层练习-拓展
分层练习-拓展
分层练习-拓展
分层练习-拓展
课堂小结
