苏教版高中数学选择性必修第一册第二章圆与方程2.1圆的方程(第1课时)课件(共55张PPT)
文档属性
| 名称 | 苏教版高中数学选择性必修第一册第二章圆与方程2.1圆的方程(第1课时)课件(共55张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 00:00:00 | ||
图片预览









文档简介
(共55张PPT)
苏教版2019高一数学(选修一)第一章 直线与方程
第一课时 圆的标准式方程
2.1 圆的方程
学习目标
1.掌握圆的定义及标准方程.
2.会用待定系数法求圆的标准方程,能准确判断点与圆的
位置关系.
3.能用圆的标准方程解决一些实际应用问题.
情景导入
人们向往圆满的人生,对于象征着团圆、和谐、美满的中秋圆月更是情有独钟!
圆是完美的图形,这节课我们继续学面直角坐标系下有关圆的知识.
明月四时好,何事喜中秋?
瑶台宝鉴,宜挂玉宇最高头.
放出白毫千丈,散作太虚一色,
万象入吾眸.星斗避光彩,
风露助清幽.
问题二:我们知道在平面直角坐标系中,两点确定一条直线,一点和倾斜角也确定一条直线,那么在什么条件下可以确定一个圆呢?
1.圆的标准式方程
新知探究
确定圆的要素:圆心和半径,
联系:圆心确定圆的位置,半径确定圆的大小.
问题一:圆是怎样定义的?
圆的定义:平面内到定点的距离等于定长的点的集合叫作圆,定点称为圆心,定长称为圆的半径.
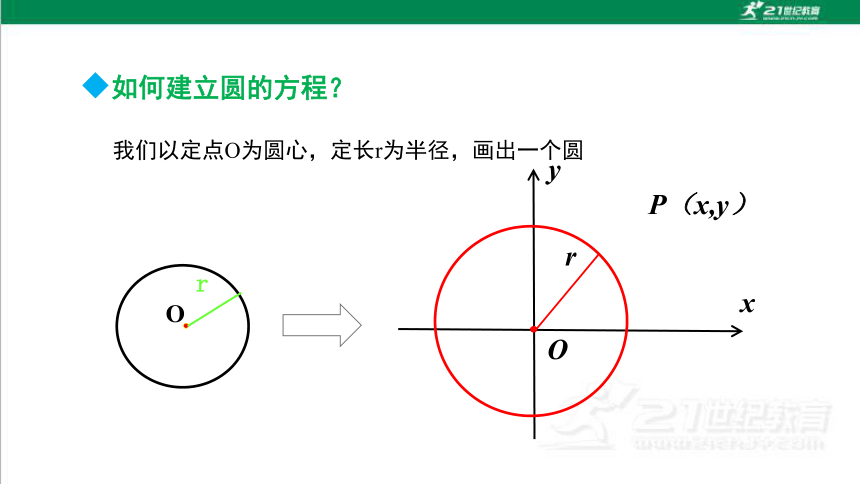
我们以定点O为圆心,定长r为半径,画出一个圆
如何建立圆的方程?
O
r
x
y
O
r
P(x,y)
x
y
O
r
P(x,y)
x
y
O
r
P(x,y)
x
y
O
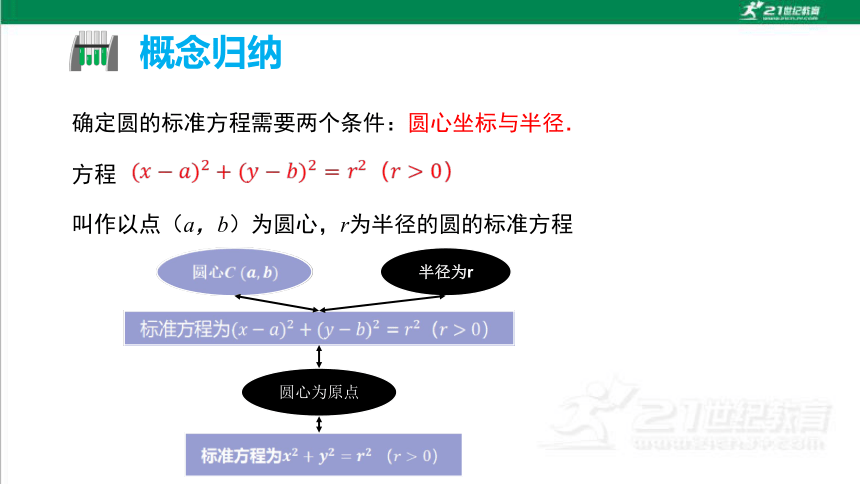
概念归纳
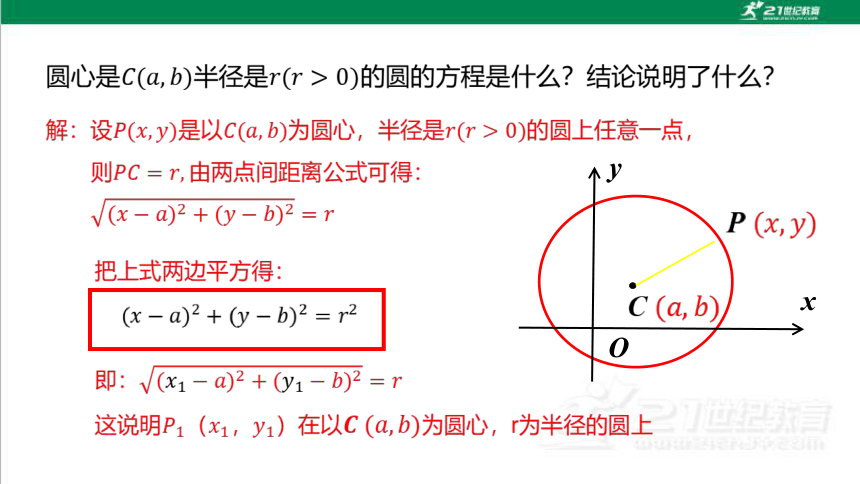
方程
确定圆的标准方程需要两个条件:圆心坐标与半径.
叫作以点(a,b)为圆心,r为半径的圆的标准方程
半径为r
圆心为原点
注意点:
(1)圆的标准方程是关于x,y的二元二次方程.
(2)确定圆的标准方程需三个独立条件以确定方程中的a,b,r.
(3)当圆心在原点即C(0,0),半径长r=1时,方程为x2+y2=1,称为单位圆.
(4)圆上的点都满足方程,满足方程的点都在圆上.
概念归纳
课本例1 求圆心是C(2,-3),且经过坐标原点的圆的方程.
课本例题
(1)以两点A(-3,-1)和B(5,5)为直径端点的圆的标准方程
是_________________________.
解析 ∵AB为直径,
∴AB的中点(1,2)为圆心,
∴该圆的标准方程为
(直接法)
典例剖析
(2)与y轴相切于点P,且圆心C坐标为(-5,-3)的圆的标准方程
为_________________________.
x
y
O
P
C
典例剖析
解析:
(待定系数法)
方法二 由几何关系知,圆心在AB的垂直平分线上,
∵AB的中点为(0,0),AB的斜率k=-1,
则AB的垂直平分线为y-0=x-0.
则所求圆的标准方程为(x-1)2+(y-1)2=4.
x
y
O
C
A(1,-1)
B(-1,1)
(几何法)
C
x
y
O
A(1,-1)
B(-1,1)
C
x
y
O
P
(1)直接法
根据已知条件,直接求出圆心坐标和圆的半径,然后写出圆的方程.
求解圆的标准方程方法:
(2)待定系数法
设方程
列方程
解方程组
得方程
由已知条件,建立关于a,b,r的方程组
解方程组,求出a,b,r
将a,b,r代入所设方程,得所求圆的标准方程
概念归纳
(3)几何法
常见的几何条件可以转化成的方程
①圆心在定直线上转化为圆心坐标满足直线方程.
②圆过定点转化为定点坐标满足圆的方程,或圆心到定点的距离等于半径.
③圆与定直线相切转化为圆心到定直线的距离等于圆的半径,或过切点垂直于切线的直线必过圆心.
④弦的垂直平分线经过圆心.
常用到中点坐标公式、两点间距离公式,有时还用到平面几何知识,
如“弦的中垂线必过圆心”“两条弦的中垂线的交点必为圆心”等.
概念归纳
(1)过点A(1,-1),B(-1,1),且圆心在直线x+y-2=0上的圆的标准方程是( )
A.(x-3)2+(y+1)2=4
B.(x+3)2+(y-1)2=4
C.(x-1)2+(y-1)2=4
D.(x+1)2+(y+1)2=4
C
练一练
方法二 本题作为选择题,可采用排除法,根据圆心在直线x+y-2=0上,
排除B,D;根据点B(-1,1)在圆上,排除A.
练一练
2.点与圆的位置关系
新知探究
问题3:点M0(x0,y0)在圆(x-a)2+(y-b)2=r2内的条件是什么?
在圆(x-a)2+(y-b)2=r2外的条件又是什么?
答:点在圆内时,点到圆心的距离小于半径,点在圆外时,点到圆心的距离大于半径.
位置关系 d与r的大小 图示 点P的坐标的特点
点在圆外 d>r (x0-a)2+(y0-b)2>r2
点在圆上 d=r (x0-a)2+(y0-b)2=r2
点在圆内 d<r (x0-a)2+(y0-b)2<r2
1.已知圆的圆心M是直线2x+y-1=0与直线x-2y+2=0的交点,且圆过点P(-5,6),求圆的标准方程,并判断点A(2,2),B(1,8),C(6,5)是在圆上,在圆内,还是在圆外?
典例剖析
判断点与圆的位置关系的两种方法
(1)几何法:主要利用点到圆心的距离与半径比较大小.
(2)代数法:把点的坐标代入圆的标准方程,判断式子两边的大小,并作出判断.
概念归纳
(1)已知圆C的标准方程是(x-2)2+(y-3)2=4,则点P(3,2)( )
A.在圆C外 B.在圆C内
C.在圆C上 D.不能确定
B
练一练
(2)若点A(a,2)不在圆(x-1)2+(y+1)2=5a的外部,则实数a的取值范围为( )
A.[1,5] B.[2,5]
C.[3,5] D.[4,5]
练一练
解析:因为点A(a,2)不在圆(x-1)2+(y+1)2=5a的外部,
所以(a-1)2+(2+1)2≤5a且a>0,
化简得a2-7a+10≤0,解得2≤a≤5.
3.圆的标准方程的实际应用
新知探究
课本例2 已知隧道的截面是半径为4 m的半圆,车辆只能在道路中心线一侧行驶,一辆宽为2.7 m,高为3 m的货车能不能驶入这个隧道?
3.已知某圆拱桥,当水面距拱顶2米时,水面宽12米,当水面下降1米后,水面宽多少米?
典例剖析
解决圆的标准方程的实际应用题时应注意以下几个方面
概念归纳
审题
建系
求解
还原
认真审题,明确题意,从题目中抽象出几何模型,明确题中已知和待求的数据
建立适当的平面直角坐标系,通过点的坐标及已知条件,求出几何模型的方程.
利用直线、圆的性质等有关知识求解
将运算结果还原为对实际问题的解释
3.一辆卡车宽1.6 m,要经过一个半圆形隧道(半径为3.6 m),则这辆卡车的平顶车篷篷顶距地面高度不得超过( )
A.1.4 m B.3.5 m
C.3.6 m D.2.0 m
B
练一练
解析 结合圆的标准方程可知,圆C的圆心坐标为(2,-1).
B
随堂练
随堂练
解析 由圆的标准方程知(x-2 023)2+(y-2 023)2=2 0242.
A
随堂练
随堂练
分层练习-基础
2.如图,圆弧形拱桥的跨度AB=12米,拱高CD=4米,则拱桥的直径为( )
A.15米 B.13米
C.9米 D.6.5米
B
B
分层练习-基础
3.圆心在直线2x+y=0上,并且经过点A(1,3)和B(4,2)的圆的半径为( )
A.3 B.4 C.5 D.6
C
B
分层练习-基础
5.(多选)已知圆M:(x-4)2+(y+3)2=25,则下列说法正确的是( )
A.圆M的圆心为(4,-3)
B.圆M的圆心为(-4,3)
C.圆M的半径为5
D.圆M被y轴截得的线段长为6
ACD
分层练习-基础
6.已知圆C1:(x+1)2+(y-1)2=1,圆C2与圆C1关于直线x-y-1=0对称,则圆C2的方程为( )
A.(x+2)2+(y-2)2=1
B.(x-2)2+(y+2)2=1
C.(x+2)2+(y+2)2=1
D.(x-2)2+(y-2)2=1
B
8.圆(x-1)2+(y-1)2=1上的点到直线x-y=2的距离的最大值是________.
分层练习-基础
7.已知三点A(3,2),B(5,-3),C(-1,3),以P(2,-1)为圆心作一个圆,使得A,B,C三点中的一个点在圆内,一个点在圆上,一个点在圆外,则这个圆的标准方程为________________.
(x-2)2+(y+1)2=13
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
10.已知圆M过A(1,-1),B(-1,1)两点,且圆心M在直线x+y-2=0上.
(1)求圆M的方程;
(2)若圆M上存在点P,使OP=m(m>0),其中O为坐标原点,求实数m的取值范围.
分层练习-巩固
11.(多选)以直线2x+y-4=0与两坐标轴的一个交点为圆心,过另一个交点的圆的方程可能为( )
A.x2+(y-4)2=20 B.(x-4)2+y2=20
C.x2+(y-2)2=20 D.(x-2)2+y2=20
AD
分层练习-巩固
12.已知直线(3+2λ)x+(3λ-2)y+5-λ=0恒过定点P,则与圆C:(x-2)2+(y+3)2=16有公共的圆心且过点P的圆的标准方程为( )
A.(x-2)2+(y+3)2=36
B.(x-2)2+(y+3)2=25
C.(x-2)2+(y+3)2=18
D.(x-2)2+(y+3)2=9
B
分层练习-巩固
13.圆(x-3)2+(y+1)2=1关于直线x+y-3=0对称的圆的标准方程是________________.
(x-4)2+y2=1
14.某圆弧形拱桥的水面跨度是20 m,拱高为4 m.现有一船宽9 m,在水面以上部分高3 m,通行无阻.近日水位暴涨了1.5 m,为此,必须加重船载,降低船身,当船身至少降低________m时,船才能安全通过桥洞.(结果精确到0.01 m)
1.22
分层练习-巩固
15.已知半径为1的圆经过点(3,4),则其圆心到原点的距离的最小值为( )
A.4 B.5 C.6 D.7
A
分层练习-巩固
分层练习-巩固
分层练习-巩固
课堂小结
1.归纳总结
(1)圆的标准方程.
(2)点与圆的位置关系.
(3)圆的标准方程的实际应用.
2.方法归纳:
直接法、几何法、待定系数法.
3.常见误区:
几何法求圆的标准方程时出现漏解情况.
苏教版2019高一数学(选修一)第一章 直线与方程
第一课时 圆的标准式方程
2.1 圆的方程
学习目标
1.掌握圆的定义及标准方程.
2.会用待定系数法求圆的标准方程,能准确判断点与圆的
位置关系.
3.能用圆的标准方程解决一些实际应用问题.
情景导入
人们向往圆满的人生,对于象征着团圆、和谐、美满的中秋圆月更是情有独钟!
圆是完美的图形,这节课我们继续学面直角坐标系下有关圆的知识.
明月四时好,何事喜中秋?
瑶台宝鉴,宜挂玉宇最高头.
放出白毫千丈,散作太虚一色,
万象入吾眸.星斗避光彩,
风露助清幽.
问题二:我们知道在平面直角坐标系中,两点确定一条直线,一点和倾斜角也确定一条直线,那么在什么条件下可以确定一个圆呢?
1.圆的标准式方程
新知探究
确定圆的要素:圆心和半径,
联系:圆心确定圆的位置,半径确定圆的大小.
问题一:圆是怎样定义的?
圆的定义:平面内到定点的距离等于定长的点的集合叫作圆,定点称为圆心,定长称为圆的半径.
我们以定点O为圆心,定长r为半径,画出一个圆
如何建立圆的方程?
O
r
x
y
O
r
P(x,y)
x
y
O
r
P(x,y)
x
y
O
r
P(x,y)
x
y
O
概念归纳
方程
确定圆的标准方程需要两个条件:圆心坐标与半径.
叫作以点(a,b)为圆心,r为半径的圆的标准方程
半径为r
圆心为原点
注意点:
(1)圆的标准方程是关于x,y的二元二次方程.
(2)确定圆的标准方程需三个独立条件以确定方程中的a,b,r.
(3)当圆心在原点即C(0,0),半径长r=1时,方程为x2+y2=1,称为单位圆.
(4)圆上的点都满足方程,满足方程的点都在圆上.
概念归纳
课本例1 求圆心是C(2,-3),且经过坐标原点的圆的方程.
课本例题
(1)以两点A(-3,-1)和B(5,5)为直径端点的圆的标准方程
是_________________________.
解析 ∵AB为直径,
∴AB的中点(1,2)为圆心,
∴该圆的标准方程为
(直接法)
典例剖析
(2)与y轴相切于点P,且圆心C坐标为(-5,-3)的圆的标准方程
为_________________________.
x
y
O
P
C
典例剖析
解析:
(待定系数法)
方法二 由几何关系知,圆心在AB的垂直平分线上,
∵AB的中点为(0,0),AB的斜率k=-1,
则AB的垂直平分线为y-0=x-0.
则所求圆的标准方程为(x-1)2+(y-1)2=4.
x
y
O
C
A(1,-1)
B(-1,1)
(几何法)
C
x
y
O
A(1,-1)
B(-1,1)
C
x
y
O
P
(1)直接法
根据已知条件,直接求出圆心坐标和圆的半径,然后写出圆的方程.
求解圆的标准方程方法:
(2)待定系数法
设方程
列方程
解方程组
得方程
由已知条件,建立关于a,b,r的方程组
解方程组,求出a,b,r
将a,b,r代入所设方程,得所求圆的标准方程
概念归纳
(3)几何法
常见的几何条件可以转化成的方程
①圆心在定直线上转化为圆心坐标满足直线方程.
②圆过定点转化为定点坐标满足圆的方程,或圆心到定点的距离等于半径.
③圆与定直线相切转化为圆心到定直线的距离等于圆的半径,或过切点垂直于切线的直线必过圆心.
④弦的垂直平分线经过圆心.
常用到中点坐标公式、两点间距离公式,有时还用到平面几何知识,
如“弦的中垂线必过圆心”“两条弦的中垂线的交点必为圆心”等.
概念归纳
(1)过点A(1,-1),B(-1,1),且圆心在直线x+y-2=0上的圆的标准方程是( )
A.(x-3)2+(y+1)2=4
B.(x+3)2+(y-1)2=4
C.(x-1)2+(y-1)2=4
D.(x+1)2+(y+1)2=4
C
练一练
方法二 本题作为选择题,可采用排除法,根据圆心在直线x+y-2=0上,
排除B,D;根据点B(-1,1)在圆上,排除A.
练一练
2.点与圆的位置关系
新知探究
问题3:点M0(x0,y0)在圆(x-a)2+(y-b)2=r2内的条件是什么?
在圆(x-a)2+(y-b)2=r2外的条件又是什么?
答:点在圆内时,点到圆心的距离小于半径,点在圆外时,点到圆心的距离大于半径.
位置关系 d与r的大小 图示 点P的坐标的特点
点在圆外 d>r (x0-a)2+(y0-b)2>r2
点在圆上 d=r (x0-a)2+(y0-b)2=r2
点在圆内 d<r (x0-a)2+(y0-b)2<r2
1.已知圆的圆心M是直线2x+y-1=0与直线x-2y+2=0的交点,且圆过点P(-5,6),求圆的标准方程,并判断点A(2,2),B(1,8),C(6,5)是在圆上,在圆内,还是在圆外?
典例剖析
判断点与圆的位置关系的两种方法
(1)几何法:主要利用点到圆心的距离与半径比较大小.
(2)代数法:把点的坐标代入圆的标准方程,判断式子两边的大小,并作出判断.
概念归纳
(1)已知圆C的标准方程是(x-2)2+(y-3)2=4,则点P(3,2)( )
A.在圆C外 B.在圆C内
C.在圆C上 D.不能确定
B
练一练
(2)若点A(a,2)不在圆(x-1)2+(y+1)2=5a的外部,则实数a的取值范围为( )
A.[1,5] B.[2,5]
C.[3,5] D.[4,5]
练一练
解析:因为点A(a,2)不在圆(x-1)2+(y+1)2=5a的外部,
所以(a-1)2+(2+1)2≤5a且a>0,
化简得a2-7a+10≤0,解得2≤a≤5.
3.圆的标准方程的实际应用
新知探究
课本例2 已知隧道的截面是半径为4 m的半圆,车辆只能在道路中心线一侧行驶,一辆宽为2.7 m,高为3 m的货车能不能驶入这个隧道?
3.已知某圆拱桥,当水面距拱顶2米时,水面宽12米,当水面下降1米后,水面宽多少米?
典例剖析
解决圆的标准方程的实际应用题时应注意以下几个方面
概念归纳
审题
建系
求解
还原
认真审题,明确题意,从题目中抽象出几何模型,明确题中已知和待求的数据
建立适当的平面直角坐标系,通过点的坐标及已知条件,求出几何模型的方程.
利用直线、圆的性质等有关知识求解
将运算结果还原为对实际问题的解释
3.一辆卡车宽1.6 m,要经过一个半圆形隧道(半径为3.6 m),则这辆卡车的平顶车篷篷顶距地面高度不得超过( )
A.1.4 m B.3.5 m
C.3.6 m D.2.0 m
B
练一练
解析 结合圆的标准方程可知,圆C的圆心坐标为(2,-1).
B
随堂练
随堂练
解析 由圆的标准方程知(x-2 023)2+(y-2 023)2=2 0242.
A
随堂练
随堂练
分层练习-基础
2.如图,圆弧形拱桥的跨度AB=12米,拱高CD=4米,则拱桥的直径为( )
A.15米 B.13米
C.9米 D.6.5米
B
B
分层练习-基础
3.圆心在直线2x+y=0上,并且经过点A(1,3)和B(4,2)的圆的半径为( )
A.3 B.4 C.5 D.6
C
B
分层练习-基础
5.(多选)已知圆M:(x-4)2+(y+3)2=25,则下列说法正确的是( )
A.圆M的圆心为(4,-3)
B.圆M的圆心为(-4,3)
C.圆M的半径为5
D.圆M被y轴截得的线段长为6
ACD
分层练习-基础
6.已知圆C1:(x+1)2+(y-1)2=1,圆C2与圆C1关于直线x-y-1=0对称,则圆C2的方程为( )
A.(x+2)2+(y-2)2=1
B.(x-2)2+(y+2)2=1
C.(x+2)2+(y+2)2=1
D.(x-2)2+(y-2)2=1
B
8.圆(x-1)2+(y-1)2=1上的点到直线x-y=2的距离的最大值是________.
分层练习-基础
7.已知三点A(3,2),B(5,-3),C(-1,3),以P(2,-1)为圆心作一个圆,使得A,B,C三点中的一个点在圆内,一个点在圆上,一个点在圆外,则这个圆的标准方程为________________.
(x-2)2+(y+1)2=13
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
10.已知圆M过A(1,-1),B(-1,1)两点,且圆心M在直线x+y-2=0上.
(1)求圆M的方程;
(2)若圆M上存在点P,使OP=m(m>0),其中O为坐标原点,求实数m的取值范围.
分层练习-巩固
11.(多选)以直线2x+y-4=0与两坐标轴的一个交点为圆心,过另一个交点的圆的方程可能为( )
A.x2+(y-4)2=20 B.(x-4)2+y2=20
C.x2+(y-2)2=20 D.(x-2)2+y2=20
AD
分层练习-巩固
12.已知直线(3+2λ)x+(3λ-2)y+5-λ=0恒过定点P,则与圆C:(x-2)2+(y+3)2=16有公共的圆心且过点P的圆的标准方程为( )
A.(x-2)2+(y+3)2=36
B.(x-2)2+(y+3)2=25
C.(x-2)2+(y+3)2=18
D.(x-2)2+(y+3)2=9
B
分层练习-巩固
13.圆(x-3)2+(y+1)2=1关于直线x+y-3=0对称的圆的标准方程是________________.
(x-4)2+y2=1
14.某圆弧形拱桥的水面跨度是20 m,拱高为4 m.现有一船宽9 m,在水面以上部分高3 m,通行无阻.近日水位暴涨了1.5 m,为此,必须加重船载,降低船身,当船身至少降低________m时,船才能安全通过桥洞.(结果精确到0.01 m)
1.22
分层练习-巩固
15.已知半径为1的圆经过点(3,4),则其圆心到原点的距离的最小值为( )
A.4 B.5 C.6 D.7
A
分层练习-巩固
分层练习-巩固
分层练习-巩固
课堂小结
1.归纳总结
(1)圆的标准方程.
(2)点与圆的位置关系.
(3)圆的标准方程的实际应用.
2.方法归纳:
直接法、几何法、待定系数法.
3.常见误区:
几何法求圆的标准方程时出现漏解情况.
