苏教版高中数学选择性必修第一册第二章圆与方程2.2直线与圆的位置关系 课件(共56张PPT)
文档属性
| 名称 | 苏教版高中数学选择性必修第一册第二章圆与方程2.2直线与圆的位置关系 课件(共56张PPT) |
|
|
| 格式 | ppt | ||
| 文件大小 | 10.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 17:51:30 | ||
图片预览







文档简介
(共56张PPT)
苏教版2019高一数学(选修一)第一章 直线与方程
2.2 直线与圆的位置关系
学习目标
1.掌握直线与圆的三种位置关系:相交、相切、相离.
2.会用代数法和几何法来判断直线与圆的三种位置关系.
情景导入
海上日出是非常壮丽的美景.在海天交于一线的天际,一轮红日慢慢升起,先是探出半个圆圆的小脑袋,然后冉冉上升,和天际线相连,再跃出海面,越来越高,展现着斑斓的霞光和迷人的风采.
在这个过程中,把太阳看作一个圆,海天交线看作一条直线,日出的过程中也体现了直线与圆的位置关系.
我们以太阳的起落为例.以蓝线为海平面所对应的水平线,圆圈为太阳!
注意观察,回答以下问题
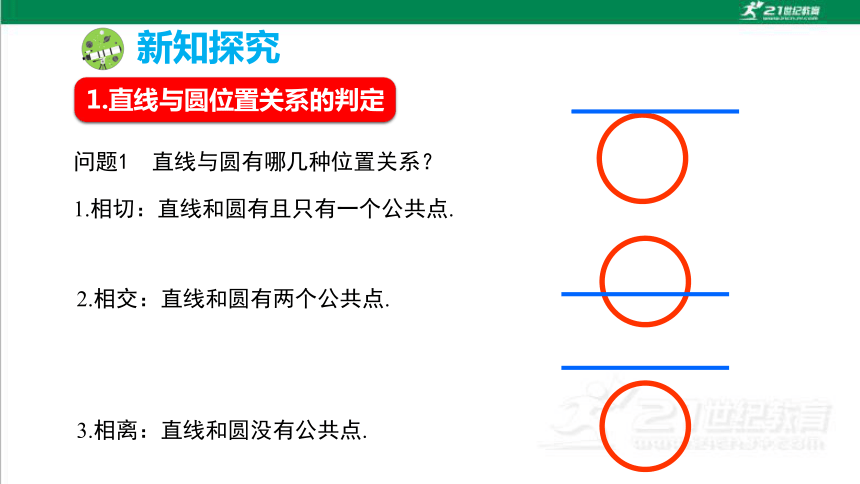
问题1 直线与圆有哪几种位置关系?
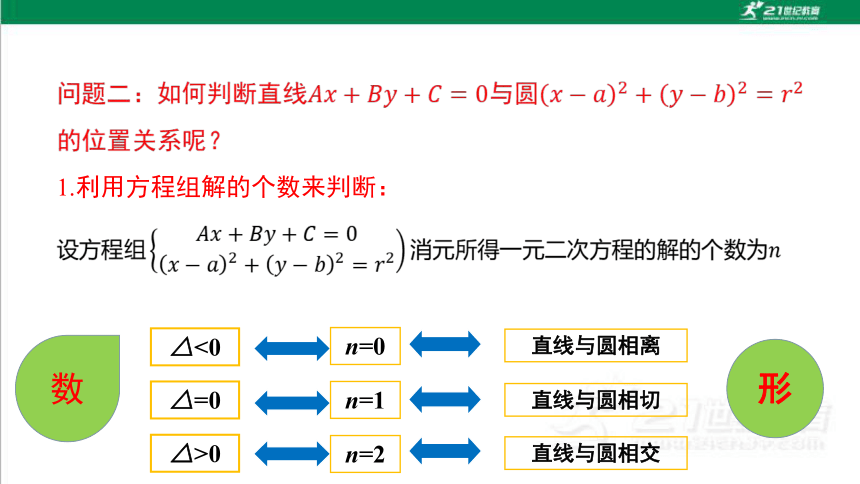
问题2 如何利用直线和圆的方程判断
它们之间的位置关系?
1.直线与圆位置关系的判定
新知探究
问题1 直线与圆有哪几种位置关系?
1.相切:直线和圆有且只有一个公共点.
2.相交:直线和圆有两个公共点.
3.相离:直线和圆没有公共点.
△<0
△=0
△>0
直线与圆相离
直线与圆相切
直线与圆相交
n=0
n=1
n=2
数
形
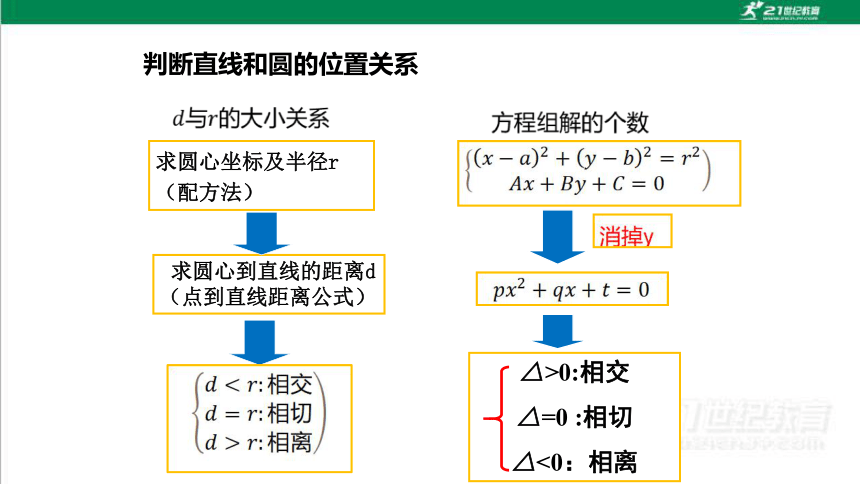
1.利用方程组解的个数来判断:
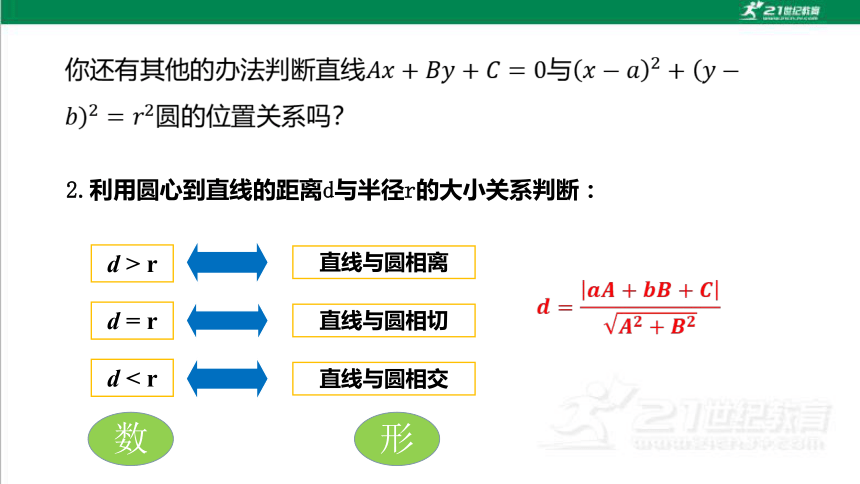
2.利用圆心到直线的距离d与半径r的大小关系判断:
d > r
d = r
d < r
直线与圆相离
直线与圆相切
直线与圆相交
数
形
求圆心坐标及半径r(配方法)
求圆心到直线的距离d (点到直线距离公式)
判断直线和圆的位置关系
△>0:相交
△=0 :相切
△<0:相离
位置关系 相交 相切 相离
公共点个数 两个 一个 零个
判定方法 d<r d=r d>r
Δ>0 Δ=0 Δ<0
直线Ax+By+C=0与圆(x-a)2+(y-b)2=r2的位置关系及判断
归纳总结
解:将直线方程与圆的方程联立方程组
所以,直线与圆相交.
方法二:
所以,直线与圆相交.
典例剖析
解:将直线方程与圆的方程联立方程组
典例剖析
所以,直线被圆截得弦长为12.
方法二:
所以,直线被圆截得弦长为12.
典例剖析
解:
典例剖析
解:设直线方程为 ,与圆方程联立:
消去 得一元二次方程:
即
整理得:
所以,所求直线方程 为
方法二:
典例剖析
自点 ,求切线 的方程.
解:
典例剖析
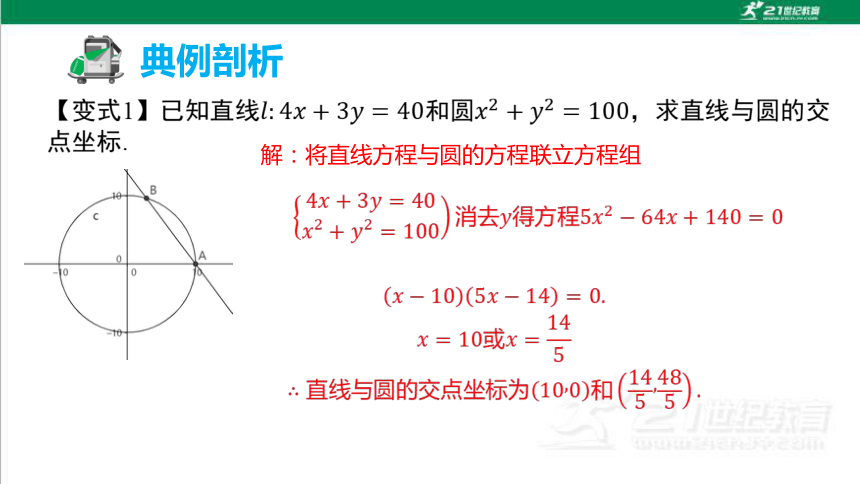
【变式4】
自点 ,求切线长.
解:
典例剖析
【变式5】
典例剖析
例2 已知直线y=x+b与圆x2+y2=2,当b为何值时,直线与圆有两个公共点?只有一个公共点?没有公共点?
典例剖析
例2 已知直线y=x+b与圆x2+y2=2,当b为何值时,直线与圆有两个公共点?只有一个公共点?没有公共点?
概念归纳
直线与圆的位置关系的判断方法
(1)几何法:由圆心到直线的距离d与圆的半径r的大小关系判断.
(2)代数法:根据直线方程与圆的方程组成的方程组解的个数来判断.
(3)直线系法:若直线恒过定点,可通过判断点与圆的位置关系来判断直线与圆的位置关系,但有一定的局限性,必须是过定点的直线系.
1.已知直线方程为mx-y-m-1=0,圆的方程为x2+y2-4x-2y+1=0.当m为何值时,直线与圆:
(1)有两个公共点;
(2)只有一个公共点;
(3)没有公共点.
练一练
练一练
练一练
练一练
(2)若圆C:x2+y2+2x-4y+3=0关于直线2ax+by+6=0对称,则由点(a,b)向圆所作的切线长的最小值是( )
A.2 B.3 C.4 D.6
C
2.过点A(-1,4)作圆(x-2)2+(y-3)2=1的切线l,则切线l的方程为__________________.
y=4或3x+4y-13=0
练一练
概念归纳
3.过圆x2+y2-2x-4y=0上一点P(3,3)的切线方程为( )
A.2x-y+9=0 B.2x+y-9=0
C.2x+y+9=0 D.2x-y-9=0
练一练
B
C
练一练
2.直线截圆所得弦长问题
新知探究
概念归纳
注意点:
(1)弦长公式的前提是判别式大于零.
(2)斜率不存在时AB=|y1-y2|.
例3 (1)求直线l:3x+y-6=0被圆C:x2+y2-2y-4=0截得的弦长AB;
(2)过点(-4,0)作直线l与圆x2+y2+2x-4y-20=0交于A,B两点,如果AB=8,求直线l的方程.
(1)求直线与圆的弦长的三种方法:
代数法、几何法及弦长公式.
(2)利用弦长求直线方程、圆的方程时,应注意斜率不存在的情况.
概念归纳
典例剖析
1.直线y=x+1与圆x2+y2=1的位置关系是( )
A.相切
B.相交但直线不过圆心
C.直线过圆心
D.相离
B
C
随堂练
3.直线x+2y-5+=0被圆x2+y2-2x-4y=0截得的弦长为________.
4.若直线x+y-m=0与圆x2+y2=2相离,则m的取值范围是__________________.
4
m<-2或m>2
随堂练
5.(2023江西临川第二中学月考)直线3x+4y+12=0与圆(x-1)2+(y+1)2=9的位置关系是 ( )
A.相交且过圆心 B.相切
C.相离 D.相交但不过圆心
D
随堂练
6.圆心为(0,1)且与直线y=2相切的圆的方程为 ( )
A.(x-1)2+y2=1 B.(x+1)2+y2=1
C.x2+(y-1)2=1 D.x2+(y+1)2=1
7.(2022江苏南通六校期末)直线3x+4y+5=0与圆x2+y2=10相交于A,B两点,则AB的长等于 ( )
A.3 B.4 C.6 D.1
C
C
分层练习-基础
1.直线3x+4y+12=0与圆(x-1)2+(y+1)2=9的位置关系是( )
A.过圆心 B.相切
C.相离 D.相交但不过圆心
2.已知圆(x-2)2+y2=9,则过点M(1,2)的最长弦与最短弦的弦长之和为( )
A.4 B.6 C.8 D.10
D
D
分层练习-基础
CD
4.若直线l:x-3y+n=0与圆x2+y2+2x-4y=0交于A,B两点,A,B关于直线3x+y+m=0对称,则实数m的值为( )
A.1 B.-1 C.-3 D.3
A
分层练习-基础
5.如图是某主题公园的部分景观平面示意图,圆形池塘以O为圆心,以45 m为半径,B为公园入口,道路AB为东西方向,道路AC经过点O且向正北方向延伸,OA=10 m,AB=100 m,现计划从B处起修一条新路与道路AC相连,且新路在池塘的外围,假设路宽忽略不计,则新路的最小长度为(单位:m)( )
A
分层练习-基础
A
7.直线l与圆x2+y2+2x-4y+a=0(a<3)相交于A,B两点,若弦AB的中点为C(-2,3),则直线l的方程为________________________.
x-y+5=0
分层练习-基础
8.过圆x2+y2=8内的点P(-1,2)作直线l交圆于A,B两点.若直线l的倾斜角为135°,则弦AB的长为________.
9.已知圆C:(x-2)2+(y-3)2=4外有一点P(4,-1),过点P作直线l.
(1)当直线l与圆C相切时,求直线l的方程;
(2)当直线l的倾斜角为135°时,求直线l被圆C所截得的弦长.
分层练习-基础
分层练习-基础
分层练习-基础
10.一艘轮船沿直线返回港口的途中,接到气象台预报,台风中心位于轮船正西70 km处,受影响的范围是半径为30 km的圆形区域,已知港口位于台风中心正北40 km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?
分层练习-基础
分层练习-巩固
11.已知坐标原点到直线l的距离为2,且直线l与圆(x-3)2+(y-4)2=49相切,则满足条件的直线l有( )
A.1条 B.2条 C.3条 D.4条
A
C
分层练习-巩固
A
14.在平面直角坐标系xOy中,若直线ax+y-2=0与圆心为C的圆(x-1)2+(y-a)2=相交于A,B两点,且△ABC为正三角形,则实数a的值是________.
0
B
分层练习-拓展
分层练习-拓展
分层练习-拓展
分层练习-拓展
1.知识清单:
(1)直线与圆的三种位置关系.
(2)圆的切线方程.
(3)弦长公式.
2.方法归纳:几何法、代数法、弦长公式法.
3.常见误区:求直线方程时忽略直线斜率不存在的情况.
课堂小结
图形
位置
相交
相切
相离
d与r关系
dd=r
d>r
d
r
d
r
d
r
方程组
解的情况
方程组有一解
方程组无解
方程组有两解
课堂小结
1.求直线与圆相交时的交点坐标需要联立方程组用方程组的解来刻画.
2.求圆的切线或弦长时则应抓住直线与圆位置关系的几何特征如垂径定理等避免求切点、交点的坐标,从而简化运算.
课堂小结
苏教版2019高一数学(选修一)第一章 直线与方程
2.2 直线与圆的位置关系
学习目标
1.掌握直线与圆的三种位置关系:相交、相切、相离.
2.会用代数法和几何法来判断直线与圆的三种位置关系.
情景导入
海上日出是非常壮丽的美景.在海天交于一线的天际,一轮红日慢慢升起,先是探出半个圆圆的小脑袋,然后冉冉上升,和天际线相连,再跃出海面,越来越高,展现着斑斓的霞光和迷人的风采.
在这个过程中,把太阳看作一个圆,海天交线看作一条直线,日出的过程中也体现了直线与圆的位置关系.
我们以太阳的起落为例.以蓝线为海平面所对应的水平线,圆圈为太阳!
注意观察,回答以下问题
问题1 直线与圆有哪几种位置关系?
问题2 如何利用直线和圆的方程判断
它们之间的位置关系?
1.直线与圆位置关系的判定
新知探究
问题1 直线与圆有哪几种位置关系?
1.相切:直线和圆有且只有一个公共点.
2.相交:直线和圆有两个公共点.
3.相离:直线和圆没有公共点.
△<0
△=0
△>0
直线与圆相离
直线与圆相切
直线与圆相交
n=0
n=1
n=2
数
形
1.利用方程组解的个数来判断:
2.利用圆心到直线的距离d与半径r的大小关系判断:
d > r
d = r
d < r
直线与圆相离
直线与圆相切
直线与圆相交
数
形
求圆心坐标及半径r(配方法)
求圆心到直线的距离d (点到直线距离公式)
判断直线和圆的位置关系
△>0:相交
△=0 :相切
△<0:相离
位置关系 相交 相切 相离
公共点个数 两个 一个 零个
判定方法 d<r d=r d>r
Δ>0 Δ=0 Δ<0
直线Ax+By+C=0与圆(x-a)2+(y-b)2=r2的位置关系及判断
归纳总结
解:将直线方程与圆的方程联立方程组
所以,直线与圆相交.
方法二:
所以,直线与圆相交.
典例剖析
解:将直线方程与圆的方程联立方程组
典例剖析
所以,直线被圆截得弦长为12.
方法二:
所以,直线被圆截得弦长为12.
典例剖析
解:
典例剖析
解:设直线方程为 ,与圆方程联立:
消去 得一元二次方程:
即
整理得:
所以,所求直线方程 为
方法二:
典例剖析
自点 ,求切线 的方程.
解:
典例剖析
【变式4】
自点 ,求切线长.
解:
典例剖析
【变式5】
典例剖析
例2 已知直线y=x+b与圆x2+y2=2,当b为何值时,直线与圆有两个公共点?只有一个公共点?没有公共点?
典例剖析
例2 已知直线y=x+b与圆x2+y2=2,当b为何值时,直线与圆有两个公共点?只有一个公共点?没有公共点?
概念归纳
直线与圆的位置关系的判断方法
(1)几何法:由圆心到直线的距离d与圆的半径r的大小关系判断.
(2)代数法:根据直线方程与圆的方程组成的方程组解的个数来判断.
(3)直线系法:若直线恒过定点,可通过判断点与圆的位置关系来判断直线与圆的位置关系,但有一定的局限性,必须是过定点的直线系.
1.已知直线方程为mx-y-m-1=0,圆的方程为x2+y2-4x-2y+1=0.当m为何值时,直线与圆:
(1)有两个公共点;
(2)只有一个公共点;
(3)没有公共点.
练一练
练一练
练一练
练一练
(2)若圆C:x2+y2+2x-4y+3=0关于直线2ax+by+6=0对称,则由点(a,b)向圆所作的切线长的最小值是( )
A.2 B.3 C.4 D.6
C
2.过点A(-1,4)作圆(x-2)2+(y-3)2=1的切线l,则切线l的方程为__________________.
y=4或3x+4y-13=0
练一练
概念归纳
3.过圆x2+y2-2x-4y=0上一点P(3,3)的切线方程为( )
A.2x-y+9=0 B.2x+y-9=0
C.2x+y+9=0 D.2x-y-9=0
练一练
B
C
练一练
2.直线截圆所得弦长问题
新知探究
概念归纳
注意点:
(1)弦长公式的前提是判别式大于零.
(2)斜率不存在时AB=|y1-y2|.
例3 (1)求直线l:3x+y-6=0被圆C:x2+y2-2y-4=0截得的弦长AB;
(2)过点(-4,0)作直线l与圆x2+y2+2x-4y-20=0交于A,B两点,如果AB=8,求直线l的方程.
(1)求直线与圆的弦长的三种方法:
代数法、几何法及弦长公式.
(2)利用弦长求直线方程、圆的方程时,应注意斜率不存在的情况.
概念归纳
典例剖析
1.直线y=x+1与圆x2+y2=1的位置关系是( )
A.相切
B.相交但直线不过圆心
C.直线过圆心
D.相离
B
C
随堂练
3.直线x+2y-5+=0被圆x2+y2-2x-4y=0截得的弦长为________.
4.若直线x+y-m=0与圆x2+y2=2相离,则m的取值范围是__________________.
4
m<-2或m>2
随堂练
5.(2023江西临川第二中学月考)直线3x+4y+12=0与圆(x-1)2+(y+1)2=9的位置关系是 ( )
A.相交且过圆心 B.相切
C.相离 D.相交但不过圆心
D
随堂练
6.圆心为(0,1)且与直线y=2相切的圆的方程为 ( )
A.(x-1)2+y2=1 B.(x+1)2+y2=1
C.x2+(y-1)2=1 D.x2+(y+1)2=1
7.(2022江苏南通六校期末)直线3x+4y+5=0与圆x2+y2=10相交于A,B两点,则AB的长等于 ( )
A.3 B.4 C.6 D.1
C
C
分层练习-基础
1.直线3x+4y+12=0与圆(x-1)2+(y+1)2=9的位置关系是( )
A.过圆心 B.相切
C.相离 D.相交但不过圆心
2.已知圆(x-2)2+y2=9,则过点M(1,2)的最长弦与最短弦的弦长之和为( )
A.4 B.6 C.8 D.10
D
D
分层练习-基础
CD
4.若直线l:x-3y+n=0与圆x2+y2+2x-4y=0交于A,B两点,A,B关于直线3x+y+m=0对称,则实数m的值为( )
A.1 B.-1 C.-3 D.3
A
分层练习-基础
5.如图是某主题公园的部分景观平面示意图,圆形池塘以O为圆心,以45 m为半径,B为公园入口,道路AB为东西方向,道路AC经过点O且向正北方向延伸,OA=10 m,AB=100 m,现计划从B处起修一条新路与道路AC相连,且新路在池塘的外围,假设路宽忽略不计,则新路的最小长度为(单位:m)( )
A
分层练习-基础
A
7.直线l与圆x2+y2+2x-4y+a=0(a<3)相交于A,B两点,若弦AB的中点为C(-2,3),则直线l的方程为________________________.
x-y+5=0
分层练习-基础
8.过圆x2+y2=8内的点P(-1,2)作直线l交圆于A,B两点.若直线l的倾斜角为135°,则弦AB的长为________.
9.已知圆C:(x-2)2+(y-3)2=4外有一点P(4,-1),过点P作直线l.
(1)当直线l与圆C相切时,求直线l的方程;
(2)当直线l的倾斜角为135°时,求直线l被圆C所截得的弦长.
分层练习-基础
分层练习-基础
分层练习-基础
10.一艘轮船沿直线返回港口的途中,接到气象台预报,台风中心位于轮船正西70 km处,受影响的范围是半径为30 km的圆形区域,已知港口位于台风中心正北40 km处,如果这艘轮船不改变航线,那么它是否会受到台风的影响?
分层练习-基础
分层练习-巩固
11.已知坐标原点到直线l的距离为2,且直线l与圆(x-3)2+(y-4)2=49相切,则满足条件的直线l有( )
A.1条 B.2条 C.3条 D.4条
A
C
分层练习-巩固
A
14.在平面直角坐标系xOy中,若直线ax+y-2=0与圆心为C的圆(x-1)2+(y-a)2=相交于A,B两点,且△ABC为正三角形,则实数a的值是________.
0
B
分层练习-拓展
分层练习-拓展
分层练习-拓展
分层练习-拓展
1.知识清单:
(1)直线与圆的三种位置关系.
(2)圆的切线方程.
(3)弦长公式.
2.方法归纳:几何法、代数法、弦长公式法.
3.常见误区:求直线方程时忽略直线斜率不存在的情况.
课堂小结
图形
位置
相交
相切
相离
d与r关系
d
d>r
d
r
d
r
d
r
方程组
解的情况
方程组有一解
方程组无解
方程组有两解
课堂小结
1.求直线与圆相交时的交点坐标需要联立方程组用方程组的解来刻画.
2.求圆的切线或弦长时则应抓住直线与圆位置关系的几何特征如垂径定理等避免求切点、交点的坐标,从而简化运算.
课堂小结
