苏教版高中数学选择性必修第一册第三章圆锥曲线与方程3.2.1双曲线的标准方程课件
文档属性
| 名称 | 苏教版高中数学选择性必修第一册第三章圆锥曲线与方程3.2.1双曲线的标准方程课件 |
|
|
| 格式 | ppt | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-17 17:53:29 | ||
图片预览







文档简介
(共44张PPT)
苏教版2019高二数学(选修一)第三章 圆锥曲线与方程
3.2.1 双曲线及其标准方程
学习目标
1.理解双曲线的定义、几何图形和标准方程的推导过程.(重点)
2.掌握双曲线的标准方程及其求法.(重点)
3.会利用双曲线的定义和标准方程解决简单的问题.(难点)
1. 椭圆的定义
和
等于常数
2a ( 2a>|F1F2|>0)
的点的轨迹.
平面内与两定点F1、F2的距离的
2.引入问题
差
等于常数
的点的轨迹是什么呢?
平面内与两定点F1、F2的距离的
|MF1|+|MF2|=2a( 2a>|F1F2|>0)
y
x
情景导入
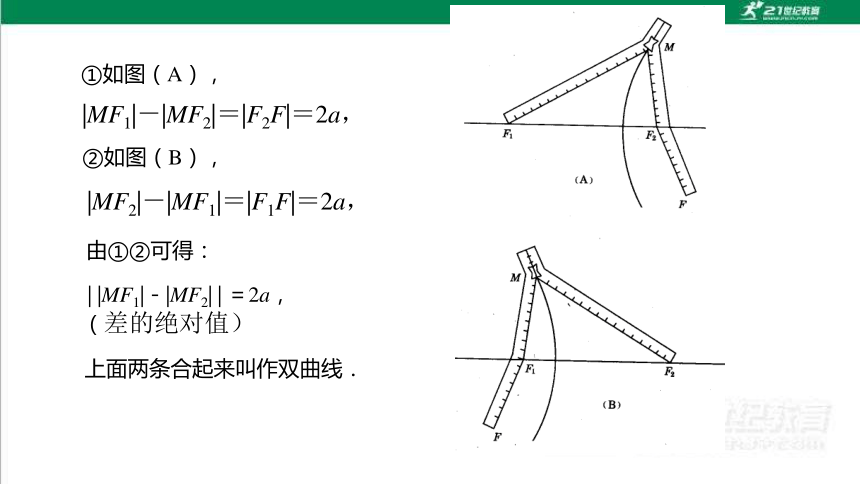
如图①所示,取一条拉链,拉开它的一部分,在拉开的两边上各选择一点,分别固定在点F1,F2上,把笔尖放在点M处,随着拉链逐渐拉开或者闭拢,笔尖所经过的点就画出一条曲线,这就是双曲线的一支.把两个固定点的位置交换,如图②所示,类似可以画出双曲线的另一支.这两条曲线合起来叫做双曲线.
双曲线上的点到两定点F1,F2的距离有何特点
情景导入
①如图(A),
|MF1|-|MF2|=|F2F|=2a,
②如图(B),
上面两条合起来叫作双曲线.
由①②可得:
| |MF1|-|MF2| | =2a,
(差的绝对值)
|MF2|-|MF1|=|F1F|=2a,
① 两个定点F1、F2——双曲线的焦点;
② |F1F2|=2c ——焦距.
(1)2a<2c ;
O
F
2
F
1
M
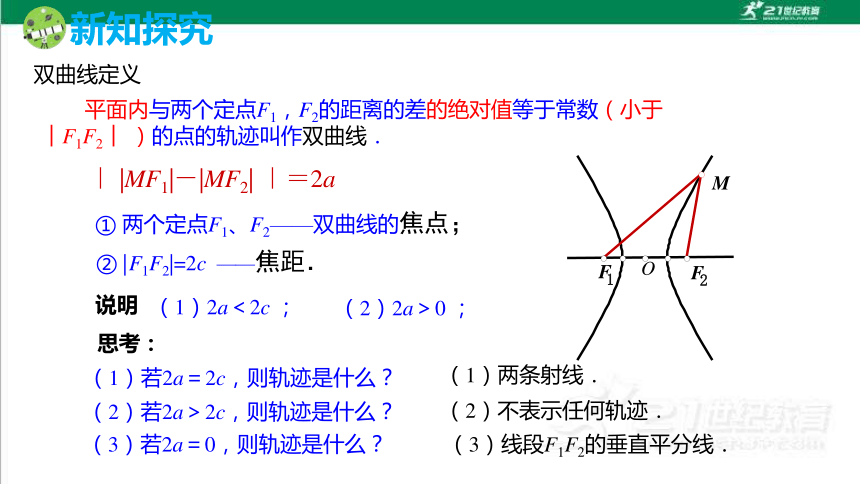
平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于︱F1F2︱ )的点的轨迹叫作双曲线.
(2)2a>0 ;
双曲线定义
思考:
(1)若2a=2c,则轨迹是什么?
(2)若2a>2c,则轨迹是什么?
说明
(3)若2a=0,则轨迹是什么?
| |MF1|-|MF2| |=2a
(1)两条射线.
(2)不表示任何轨迹.
(3)线段F1F2的垂直平分线.
新知探究
求曲线方程的步骤:
双曲线的标准方程
1. 建系.
以F1,F2所在的直线为x轴,线段F1F2的中点为原点建立直角坐标系.
2.设点.
设M(x , y),则F1(-c,0),F2(c,0).
3.列式
|MF1| -|MF2|=±2a.
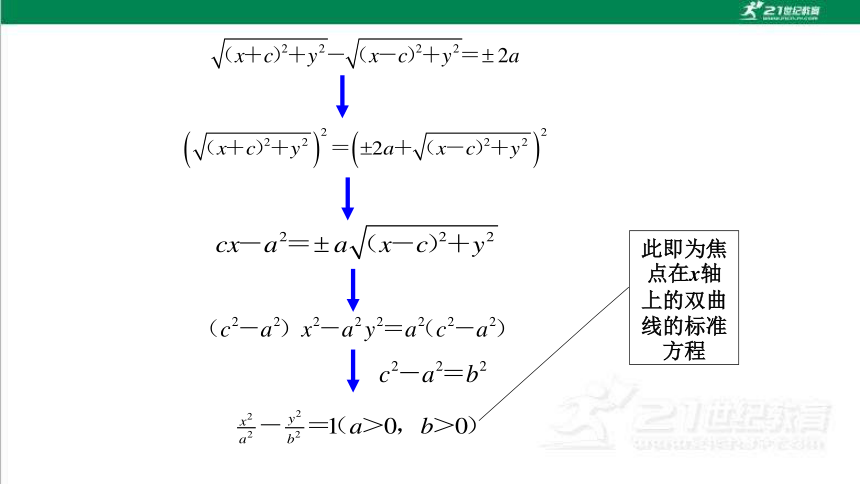
4.化简
O
F
2
F
1
M
此即为焦点在x轴上的双曲线的标准方程
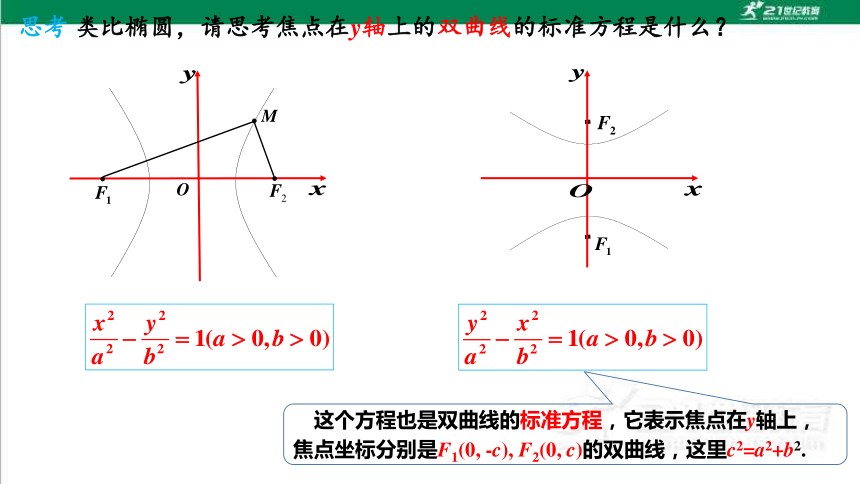
思考 类比椭圆,请思考焦点在y轴上的双曲线的标准方程是什么?
O
M
这个方程也是双曲线的标准方程,它表示焦点在y轴上,焦点坐标分别是F1(0, -c), F2(0, c)的双曲线,这里c2=a2+b2.
例1.已知双曲线的两个焦点分别为F1(-5,0),F2(5,0),双曲线上一点到F1,F2的距离之差的绝对值等于8,求该双曲线的标准方程.
课本例题
课本例题
例3.已知A,B两地相距800m,一炮弹在某处爆炸,在A处听到爆炸声的时间比在B处迟2s,设声速为340m/s.
(1)爆炸点在什么曲线上?
(2)求这条曲线的方程.
【解析】解(1)根据题意,设M为爆炸点,
在A处听到爆炸声的时间比在B处迟2s,则有
|MA|-|MB|=340×2=680<|AB|;
因为爆炸点离A点比离B点距离更远,
所以爆炸点在以A,B为焦点且距B较近的双曲线的一支上;
课本例题
例3.已知A,B两地相距800m,一炮弹在某处爆炸,在A处听到爆炸声的时间比在B处迟2s,设声速为340m/s.
(1)爆炸点在什么曲线上?
(2)求这条曲线的方程.
x
y
o
M
B
A
确定爆炸点或出事地点的位置,在军事上或抢险救灾时都有重要意义.从例3看出,利用两个不同的观测点,可以确定爆炸点所在的曲线,但不能完全确定爆炸点的位置,要有几个观测点才能确定爆炸点的位置呢
答 再增设一个观测点C,利用B、C(或A、C)两处测得的爆炸声的时间差,可以求出另一个双曲线的方程,解这两个方程组成的方程组,就能确定爆炸点的准确位置.这是双曲线的一个重要应用.
课本例题
∴所求公共点的坐标为(-2,0),(4,3).
1.在△ABC中,BC的长为2,|AB-AC|=1,试确定点A在怎样的曲线上运动.
【解析】解:因为在△ABC中,BC的长为2,
又|AB-AC|=1<2,
所以点A在以B,C位焦点,到两个焦点距离之差的绝对值为1的双曲线上运动.
课本练习
2.求适合下列条件的双曲线的标准方程:
(1)c=5.b=3,焦点在x轴上;
(2)焦点为F1(0,-6),F2(0,6),且a=3;
(3)a=4,b=3.
【解析】解:因为双曲线的一个焦点坐标为(0,3),
所以双曲线的焦点在y轴上,
B
故选:B.
易错警示 双曲线定义的应用
错解分析:出错的根本原因是忽略了双曲线中的一个隐含条件.双曲线上的点到任一焦点的距离都大于等于c-a,从而两解中要舍掉一个.
防范措施:关注隐含条件的应用
在求解双曲线上的点到焦点的距离时,一定要注意隐含的条件,实际上就是定义中的点需要满足的条件.如本例中|PF2|≥2.
典例剖析
题型一:双曲线定义的应用
解 (1)设|MF1|=16,根据双曲线的定义知||MF2|-16|=6,即|MF2|-16=±6.
解得|MF2|=10或|MF2|=22.
归纳总结
题型二:求双曲线的标准方程
典例剖析
思路分析(1)结合a的值设出标准方程的两种形式,将点A的坐标代入求解.
(2)因为焦点相同,所以所求双曲线的焦点也在x轴上,且c2=16+4=20,利用待定系数法求解,或设出统一方程求解.
(3)双曲线焦点的位置不确定,可设出一般方程求解.
归纳总结
(1)若该方程表示双曲线,求实数k的取值范围;
(2)若该方程表示焦点在y轴上的双曲线,求实数k的取值范围.
思路分析根据双曲线方程的特征建立不等式(组)求解.
题型三:双曲线标准方程的应用
典例剖析
归纳总结
随堂检测
1.已知平面上定点F1,F2及动点M,命题甲:||MF1|-|MF2||=2a(a为常数),
命题乙:M点的轨迹是以F1,F2为焦点的双曲线,则甲是乙的 ( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
【答案】B
【答案】D
3.在方程mx2-my2=n中,若mn<0,则方程的曲线是 ( )
A.焦点在x轴上的椭圆 B.焦点在x轴上的双曲线
C.焦点在y轴上的椭圆 D.焦点在y轴上的双曲线
【答案】D
【答案】A
课堂小结
苏教版2019高二数学(选修一)第三章 圆锥曲线与方程
3.2.1 双曲线及其标准方程
学习目标
1.理解双曲线的定义、几何图形和标准方程的推导过程.(重点)
2.掌握双曲线的标准方程及其求法.(重点)
3.会利用双曲线的定义和标准方程解决简单的问题.(难点)
1. 椭圆的定义
和
等于常数
2a ( 2a>|F1F2|>0)
的点的轨迹.
平面内与两定点F1、F2的距离的
2.引入问题
差
等于常数
的点的轨迹是什么呢?
平面内与两定点F1、F2的距离的
|MF1|+|MF2|=2a( 2a>|F1F2|>0)
y
x
情景导入
如图①所示,取一条拉链,拉开它的一部分,在拉开的两边上各选择一点,分别固定在点F1,F2上,把笔尖放在点M处,随着拉链逐渐拉开或者闭拢,笔尖所经过的点就画出一条曲线,这就是双曲线的一支.把两个固定点的位置交换,如图②所示,类似可以画出双曲线的另一支.这两条曲线合起来叫做双曲线.
双曲线上的点到两定点F1,F2的距离有何特点
情景导入
①如图(A),
|MF1|-|MF2|=|F2F|=2a,
②如图(B),
上面两条合起来叫作双曲线.
由①②可得:
| |MF1|-|MF2| | =2a,
(差的绝对值)
|MF2|-|MF1|=|F1F|=2a,
① 两个定点F1、F2——双曲线的焦点;
② |F1F2|=2c ——焦距.
(1)2a<2c ;
O
F
2
F
1
M
平面内与两个定点F1,F2的距离的差的绝对值等于常数(小于︱F1F2︱ )的点的轨迹叫作双曲线.
(2)2a>0 ;
双曲线定义
思考:
(1)若2a=2c,则轨迹是什么?
(2)若2a>2c,则轨迹是什么?
说明
(3)若2a=0,则轨迹是什么?
| |MF1|-|MF2| |=2a
(1)两条射线.
(2)不表示任何轨迹.
(3)线段F1F2的垂直平分线.
新知探究
求曲线方程的步骤:
双曲线的标准方程
1. 建系.
以F1,F2所在的直线为x轴,线段F1F2的中点为原点建立直角坐标系.
2.设点.
设M(x , y),则F1(-c,0),F2(c,0).
3.列式
|MF1| -|MF2|=±2a.
4.化简
O
F
2
F
1
M
此即为焦点在x轴上的双曲线的标准方程
思考 类比椭圆,请思考焦点在y轴上的双曲线的标准方程是什么?
O
M
这个方程也是双曲线的标准方程,它表示焦点在y轴上,焦点坐标分别是F1(0, -c), F2(0, c)的双曲线,这里c2=a2+b2.
例1.已知双曲线的两个焦点分别为F1(-5,0),F2(5,0),双曲线上一点到F1,F2的距离之差的绝对值等于8,求该双曲线的标准方程.
课本例题
课本例题
例3.已知A,B两地相距800m,一炮弹在某处爆炸,在A处听到爆炸声的时间比在B处迟2s,设声速为340m/s.
(1)爆炸点在什么曲线上?
(2)求这条曲线的方程.
【解析】解(1)根据题意,设M为爆炸点,
在A处听到爆炸声的时间比在B处迟2s,则有
|MA|-|MB|=340×2=680<|AB|;
因为爆炸点离A点比离B点距离更远,
所以爆炸点在以A,B为焦点且距B较近的双曲线的一支上;
课本例题
例3.已知A,B两地相距800m,一炮弹在某处爆炸,在A处听到爆炸声的时间比在B处迟2s,设声速为340m/s.
(1)爆炸点在什么曲线上?
(2)求这条曲线的方程.
x
y
o
M
B
A
确定爆炸点或出事地点的位置,在军事上或抢险救灾时都有重要意义.从例3看出,利用两个不同的观测点,可以确定爆炸点所在的曲线,但不能完全确定爆炸点的位置,要有几个观测点才能确定爆炸点的位置呢
答 再增设一个观测点C,利用B、C(或A、C)两处测得的爆炸声的时间差,可以求出另一个双曲线的方程,解这两个方程组成的方程组,就能确定爆炸点的准确位置.这是双曲线的一个重要应用.
课本例题
∴所求公共点的坐标为(-2,0),(4,3).
1.在△ABC中,BC的长为2,|AB-AC|=1,试确定点A在怎样的曲线上运动.
【解析】解:因为在△ABC中,BC的长为2,
又|AB-AC|=1<2,
所以点A在以B,C位焦点,到两个焦点距离之差的绝对值为1的双曲线上运动.
课本练习
2.求适合下列条件的双曲线的标准方程:
(1)c=5.b=3,焦点在x轴上;
(2)焦点为F1(0,-6),F2(0,6),且a=3;
(3)a=4,b=3.
【解析】解:因为双曲线的一个焦点坐标为(0,3),
所以双曲线的焦点在y轴上,
B
故选:B.
易错警示 双曲线定义的应用
错解分析:出错的根本原因是忽略了双曲线中的一个隐含条件.双曲线上的点到任一焦点的距离都大于等于c-a,从而两解中要舍掉一个.
防范措施:关注隐含条件的应用
在求解双曲线上的点到焦点的距离时,一定要注意隐含的条件,实际上就是定义中的点需要满足的条件.如本例中|PF2|≥2.
典例剖析
题型一:双曲线定义的应用
解 (1)设|MF1|=16,根据双曲线的定义知||MF2|-16|=6,即|MF2|-16=±6.
解得|MF2|=10或|MF2|=22.
归纳总结
题型二:求双曲线的标准方程
典例剖析
思路分析(1)结合a的值设出标准方程的两种形式,将点A的坐标代入求解.
(2)因为焦点相同,所以所求双曲线的焦点也在x轴上,且c2=16+4=20,利用待定系数法求解,或设出统一方程求解.
(3)双曲线焦点的位置不确定,可设出一般方程求解.
归纳总结
(1)若该方程表示双曲线,求实数k的取值范围;
(2)若该方程表示焦点在y轴上的双曲线,求实数k的取值范围.
思路分析根据双曲线方程的特征建立不等式(组)求解.
题型三:双曲线标准方程的应用
典例剖析
归纳总结
随堂检测
1.已知平面上定点F1,F2及动点M,命题甲:||MF1|-|MF2||=2a(a为常数),
命题乙:M点的轨迹是以F1,F2为焦点的双曲线,则甲是乙的 ( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
【答案】B
【答案】D
3.在方程mx2-my2=n中,若mn<0,则方程的曲线是 ( )
A.焦点在x轴上的椭圆 B.焦点在x轴上的双曲线
C.焦点在y轴上的椭圆 D.焦点在y轴上的双曲线
【答案】D
【答案】A
课堂小结
